竞争阶段天然气管道运输的博弈定价模型

陈月璇，王菊娥

（中国石油大学（华东）经济管理学院，山东青岛 266580）

0 引言

天然气除了管道运输外，LNG、NGH等运输方式表现出巨大的发展潜力，拥有广阔的发展前景，这些运输方式间的竞争也越来越激烈，从而使天然气管道运输处于竞争阶段。在这一阶段至少存在三种运输方式的竞争：一是管道运输网络间的竞争；二是LNG运输方式的替代竞争；三是NGH运输方式的替代竞争。面对不再单一的运输方式，消费者选择的余地愈来愈大，他们会在比较中选用最优惠的运输方式，对价格的反应也更加敏感，从而导致价格和服务竞争日益激烈。在竞争阶段，如何确定合理的管道运输价格成为管道运营商亟待解决的问题。

在天然气工业的成熟期，天然气企业竞争的集中在天然气的运输方式上，因此天然气运输企业间的竞争不仅仅是两个企业间的博弈，而是一种在企业的“行为理性”基础上的“非合作博弈”。“行为理性”主要是指企业实现其自身利益最大化的市场活动目的，“非合作博弈”指参与市场活动中的各个个体之间没有串谋的情况发生。这种博弈的结果就存在“纳什均衡”。因此利用博弈论对管道运输定价问题进行探讨成为可能。

1 基本假设

(1)为了理论阐述的方便，将所有竞争对手合并，视为一个对手，让其与某一管道运营商进行价格博弈。对某一具体的管道运营商而言，他面临的竞争对手可能不计其数，但在特定区域和特定时期对其威胁最大的只有一家，如果能够在与其最强的对手博弈中取得优势，这种竞争优势相对于其他多家竞争对手同样是有优势的。因此，将所有竞争对手合并视为一个威胁最大的竞争对手进行博弈具有合理性。

(2)根据博弈论，可以假设天然气运输价格市场的博弈主要以下几个特点：①非合作博弈表现明显。由于企业在进行市场活动时，其最终目的都是追逐自身利益的最大化，因此在非合作的竞争方面的博弈表现十分明显。②博弈具有顺序。市场价格的竞争主要体现在服务价格的变化上面，这也是企业博弈时应用最为广泛的竞争手段。但价格下降不可能是所有企业同时下降，一定是一个企业的服务价格首先下降后，另一个企业跟着下降其服务价格，从而保证本身企业仍然具备市场的竞争力。因此，价格调整的过程是一个动态且具有先后顺序的过程。③信息透明化的博弈。企业的价格变动是面对消费者而言的，所以自身企业的服务价格信息是可以通过消费市场而传递到对手面前，同样，企业自身也可以通过消费市场来获取对手的服务价格信息。

(3)企业的竞争过程是全方位的、综合能力的较量，竞争不仅存在于价格领域，在运输服务质量、企业信誉等方面也存在竞争。运输价格、服务质量、企业信誉等都会影响运输的需求量，为了简化研究，设价格与需求量为线性关系，即满足

式(1)中，Qi为运输商i的运输需求，σj≥0表示运输商j与运输商i运输服务间的替代系数，也可以表达为为运输商i市场运输价格，ai,bi,σj作为参数可以从过去的销售数据利用回归分析方法一一得出。

(4)假设运输商i的单位运输成本为ci，固定成本为FCi，总成本函数为

同理ci,FCi作为参数可以从过去的生产数据利用回归分析方法一一得出。

则企业利润为

式(3)中，πi为运输商i的利润。

2 动态博弈阶段的定价模型

上文分析到，在双方进行博弈时，其特点之一是具体先后顺序的。即一方在进行价格变化后，另一方根据价格的变化来改变自身的价格或企业的营销策略。在博弈过程中，企业的一次行动就成为博弈过程中的一个阶段。由于双方都会根据对方的策略而改变自身，因此，在整个博弈过程中，会根据对方调整自身的经营策略，从而出现多个博弈阶段。所以在博弈过程，价格模型是一个动态的变化过程。为了方便叙述和理解，一般采用“两阶段”模式进行博弈动态分析。在双方博弈的过程中，各方对于对方的利益所在都十分了解，而且即使对方根据市场情况而改变了自身的经营策略，同样可以在较短的时间内被对方获悉。双方的信息在整个博弈过程中是公开且平等的。企业1在采用了其经营策略后，企业2为了保证自身的最大利益也会采取相关措施，而企业1同样会根据企业2的策略改变自身的经营方式。这就是动态博弈的基本过程，具体分析如下：

(1)在第二阶段时，给定参与人(管道运输商)1在第一阶段的选择s1,参与人2面临的问题为，设其最优解为

(2)在第一阶段，参与人1预期参与人2在第二阶段的选择将按进行决策，于是参与人1面临的问题为：为最优解，则均衡解为

具体公式推倒过程如下：

天然气管道运输商1根据市场情况决定自己的运输价格，管道运输商2在了解管道输商1的价格情况下，决定自己的运输价格。

①在第二阶段时，给定天然气管道运输商1在第一阶段的价格选择P1,运输商2面临的问题是

求解：

其最优解为：

②在第一阶段，天然气管道运输商1预期管道运输商2在第二阶段的选择将按行定价，于是运输商1面临的问题为：

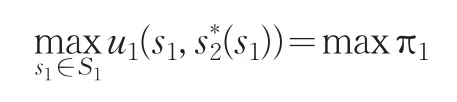
求解方程组：

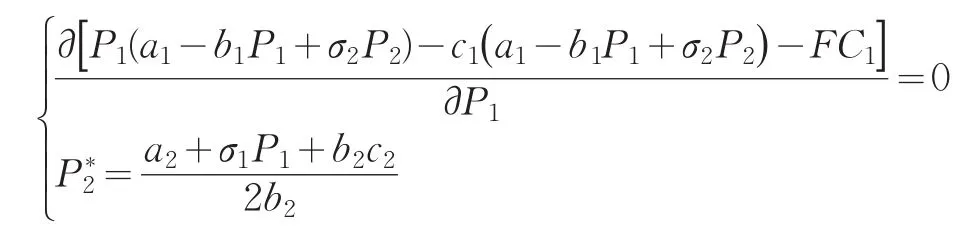
最优解为：

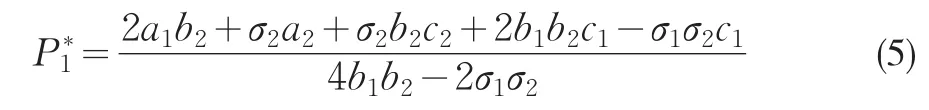
将P*1代入式(4)得：

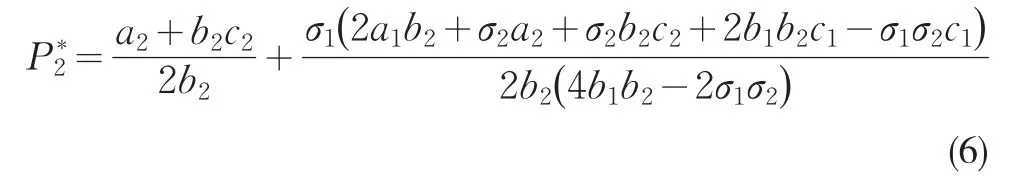
通过公式推导，我们可以求出动态博弈的均衡解(P*1,P*2)。通过上述求解过程我们可以看到，决定P*i（价格）的影响因素主要包括a、b（函数参数），σ（替代系数）以及c（边际运输成本），而固定成本则没有影响到最后的价格。对于上述公式中涉及到的参数，我们可以通过管道运输商的销售资料进行数据统计分析，然后利用回归分析法得到最后确定的参数、系数。这样，就可以得到最后的博弈定价的确定价格。但在企业的实际运营过程中，其经营策略的制定不仅是根据市场需求，还包括竞争对手的经营策略。所以，变动成本就成为企业调价环节中的重要影响因素。

在这里，为了满足模型在实际应用方面的有效性，我们以影响最大的变动成本c为因素进行讨论，的变量在影响条件大的情况下讨论方式与其类似。

在一段时期的博弈均衡后，由于各种外界原因导致运营商1的成本c变动，但由于并不影响对方的定价，因此只需将改变后的数值代入公式（5）（6）中即可得出新外界条件下的最优定价值。

事实上，在两阶段动态博弈的过程中，运输商1为了做出利益最大化的定价策略，不得不考虑竞争对手以及其他诸如设立进入壁垒等综合因素。当然其中最主要的因素取决定于竞争对手的定价策略，因此在博弈过程中，可以视为双方不同的动态定价导致双方不同的利益结果，最后达到双方均衡的程度。这其中仅存在两种状态，即双方未达到均衡和双方达到均衡，当双方处于未达到均衡的状态时，双方都有利益最大化的动机去通过时间的不断重复博弈以达到均衡的利益最大化状态。为了研究方便，同时不影响结论，可以将时间的不断重复博弈用空间的不同定价策略一次性体现出来。即假设空间中有数目足够多的商家1，在面对竞争对手的定价策略时，各个商家1皆采取不同的定价策略，由于商家1的数目足够多，因此这些定价策略涵盖了商家1在竞争对手某个定价策略下所能采取的所有可能定价策略，自然也就包含了利益最大化的状态。进一步将这些商家1采取的定价策略以及利益结果同时在空间坐标中用点集的方式表达，当商家1的数目足够多，涵盖的可能性足够多时，商家1的利益散点则构成了商家1的利益曲面。此时就完成了将时间上的不断重复博弈达到均衡转化为空间上的商家1决策利益曲面，因此仅仅需要在曲面上得出相关的点，并分析相关的坐标数值以及曲面的性质，就可以得出商家1在竞争对手某一定价策略下的定价状态，同样可以很容易得出最优的定价组合。

3 应用实例

利用回归分析方法，通过对管道运输商1和管道运输商2历史数据进行分析，得出他们的需求函数和成本函数的参数分别为即这两个管道运输商的需求曲线分别为:

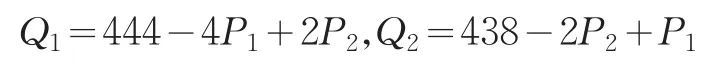
各自的成本函数分别为:

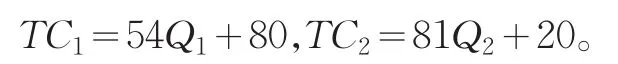
将a1=444、b1=4、σ1=2、c1=54、a2=438、b2=2、σ2=1、c2=81分别代入公式（5）和（6）中P*1≐112，P*2≐166

如果不存在“非合作博弈”问题，而是这两家管道运输商在竞争中都追求利润最大化，利用经济学原理，他们的利润分别是:

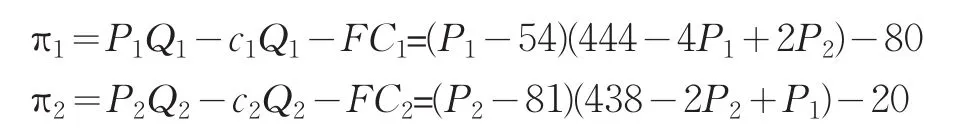
根据市场均衡条件得:

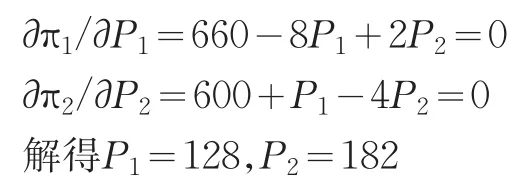
运输商1在考虑对手定价同时，考虑其他如打压竞争对手等综合因素下从而给出相应的定价。因此，理论上在任一给定的对手定价下运输商1的不同定价会带来不同的利润后果。即运输商1的利润由自身和对手共同决定，可抽象为如下函数：

π1=P1Q1-c1Q1-FC1=(P1-54)(444-4P1+2P2)-80

因此可以得出运输商1的利润曲面如图1。

图1 运输商1利润曲面图

由图1中可以直观的看出，运输商1的利润随着双方定价的增高而加速下降。在不同的竞争对手定价情况下，运输商1的定价均存在利润最大化，并且呈现出递减的趋势。

同理考虑运输商2，容易得到运输商2利润函数：

π2=P2Q2-c2Q2-FC2=(P2-81)(438-2P2+P1)-20

同理可得运输商2的利润曲面如图2。

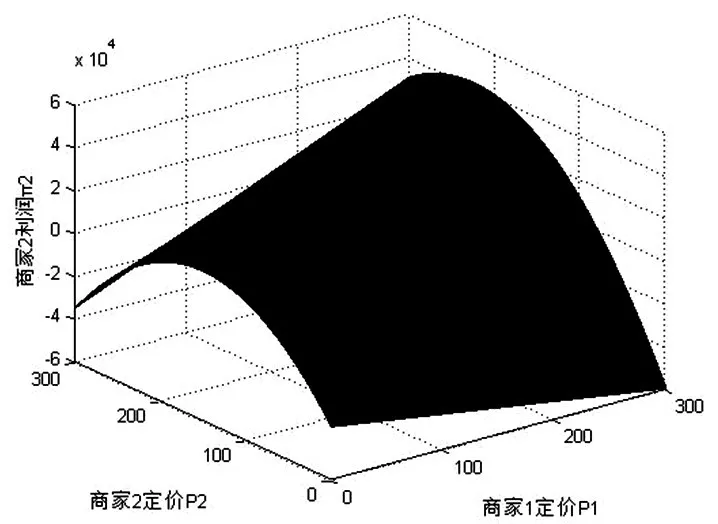
图2 运输商2利润曲面图

由图2中可以看出，随着运输商1的定价，运输商2选择相应的定价后取得的利润存在最大收益。并且利润受到定价的影响比较明显，利润曲面的曲率变动比较大。另外，还有若干情况下存在利润为负值的情况，即说明运输商间存在违反市场经济规律的不正当竞争情况。

图3为运输商的利润曲面图，灰色代表运输商1的利润，黑色代表运输商2的利润。利润由双方定价共同决定。

若由上述博弈定价模型分析，当在任一双方定价点时，存在两种情况，分别为双方利润达到各自最大和未达到各自最大。例如某种情况下双方的定价情况为点N1，此时运输商1为了利润最大化，通过修改定价P1将定价点移动到N2，同理，此时运输商2也修改定价，经过如此反复的动态博弈过程后，达到双方利润在对方定价下均为最大的情形，即达到博弈均衡点N3。此时，在没有外界介入影响的情况下双方都没有动机去更改定价，达到稳定定价点N3（112,166），这与上述两阶段动态定价模型得出的结果相一致，说明了模型的正确性和有效实用性。

若在市场经济中，双方管道运输商都将追求利益最大化。前文已经解出得点（128,182）。在图3中也可以明显看出，即为点P1max和P2max，利润值都大于博弈均衡点N3并且均大于任一定价点，同时价格也高于均衡价格，即说明运输商仍然有降价的空间，未达到市场配置的最优化。

即曲面论证表现出的定价结果与两阶段动态定价模型相一致，因此在通常的竞争博弈定价中，两阶段动态定价模型具有普遍实用意义。

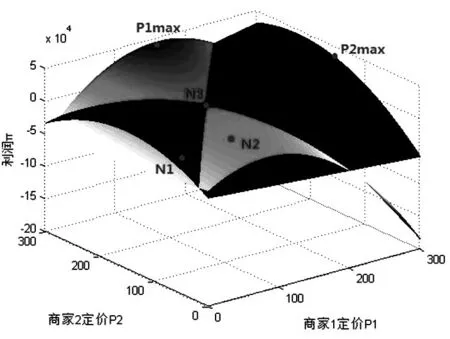
图3 运输商利润曲面图

从以上分析结果可知，市场均衡价格高于博弈定价时的最优价格，说明同样都追求利润最大化，在市场均衡条件下的均衡价格要比非合作博弈条件下的最优价格高，利润空间也更大，但对消费者不利。为了追求更高的效率，运输商仍有降价的空间，经过降价最终可实现纳什均衡解，使博弈定价更合理。这种定价方法与实际是吻合的。

4 结论

管道运输博弈定价是一个动态的博弈过程，通过以上分析可以得出以下结论：

(1)信息的完全性和两个管道运输商是博弈定价的假设基础。当存在不完全信息时，必将出现恶性竞争局势，所以各管道运输商应当尽量了解行业和竞争对手的价格信息。如果是多个管道运输商之间的博弈定价活动，可以根据各自特点将它们进行合并，得到的结论是企业联合、兼并后的最优结果，这为研究整个行业发展战略和行业定价问题提供了很好的模型基础和理论依据。

(2)管道运输商的需求函数、成本函数都是线性方程，这种理想化的状态与实际可能存在疑义，但这种方法为我们进一步研究管道运输商定价问题提供了较为重要的依据。

(3)博弈定价中的最优价格受到各自的需求函数、成本函数影响，另外还受到管道运输商间运输方式的替代效应影响，这种影响最终表现为受各自的生产成本(边际成本或单位可变成本)的影响。因此事先研究和建立这些函数模型，确定这些函数的参数是解决该定价问题的关键。

(4)任何一个管道运输商在这种博弈定价基础上都能实现利润最大化，各自利润空间虽然较大，但是对消费者来说这种博弈定价方法所得的价格比市场均衡条件下的均衡价格要低，因此效率也更高。

(5)如果通过博弈定价方式确定的价格仍然较高时，为了保护消费者的行为，政府可以通过限价或补贴等方式来影响各管道运输商的价格行为。

[1]Philip Kotler.Marketing Management（10thEdition）[M].New Jersey Prentice Hail.2000.

[2]李俊.能源效率研究综述[J].邵阳学院学报（社会科学版）,2010,（2）.

[3]谢识予.经济博弈论[M].上海：复旦大学出版社,2002.

[4]刘晓岚.国外资源类企业跨国并购的经验及其借鉴[J].邵阳学院学报（社会科学版）,2011,（1）.

[5]陈艳莹,原毅军.交叉补贴与网络中介的价格竞争[J].财经研究,2003,(10).

[6]王煜,胡连东.电信市场价格竞争的博弈论分析[J].黑龙江通信技术,2002,(12).