基于高频数据的赋权已实现极差β估计量的构建

郭名媛

0 引言

Markowitz提出的现代证券组合投资理论运用数理统计的方法全面而细致地分析了何为最优的资产结构和如何选择最优的资产结构。一般而言，投资风险越大，其期望收益也就越高。投资者在权衡收益和风险时，以其对投资风险的偏好来进行证券资产的选择。资本资产定价模型(CAPM)与Markowitz的现代证券组合投资理论有着极其密切的关系。对于投资者来说，有效投资组合中单个证券的总风险中只有系统风险这部分对有效投资组合的风险做出贡献，每个证券的非系统风险则在有效投资组合中消失。而资本资产定价模型中的β数则用来衡量有效投资组合中单个证券的风险。资本资产定价模型(CAPM)是以市场收益作为影响因子的单因子模型，具有简便、易于操作的特点。虽然CAPM也遭到了某些批评，然而对于CAPM的理论研究和实际应用仍然十分的活跃，也证明了其有很大的实用价值。国内对资本资产定价模型的研究主要始于20世纪90年代，虽然CAPM在中国股票市场的适用性是一个问题。但是，它所包含的基于Markowitz的资产组合理论，它对风险的分析，对市场组合及其替代物的论述以及它对风险与收益之间关系的描述，对中国的股票市场有很大的指导意义。充分利用CAPM较强的逻辑性、实用性，通过对股票市场的实证分析和理论研究，有利于发现问题，推动我国股市的发展。因此，正确确定CAPM中的系统风险系数β非常重要。

大多数国内外的实证研究证明了系统风险系数β是可变的，投资者的风险厌恶程度与经济所处的状态相关，在股票市场的不同的时期，股票的系统风险系数β会有所变化。De Santis,Gerard(1997)[1]证明系统风险系数β随时间的改变而改变。Bekaert,Harvey(1995)[2]在检验世界金融市场之间的协同性的同时，发现系统风险系数β随着国内和世界的信息变量的改变而改变。Fabozzi，Frank(1977)[3]研究了在不同市场态势下证券β值的差异及稳定性，并指出当市场状况从牛市转向熊市时，β值较不稳定。然而国内外的实证研究主要是采用低频数据进行的[1～12]。

随着计算机技术和通讯技术的进步，采集和存储高频金融数据已经成为了可能。这使得采用高频数据来度量系统风险系数β成为了可能。这种方法相对于采用低频数据更能够充分利用股票数据的日内信息。

本文拟采用高频金融数据，通过赋权已实现极差方差和赋权已实现极差协方差来度量市场收益的方差和股票收益与市场收益的协方差，构建赋权已实现极差β估计量，对系统风险系数β进行研究。

1 已实现极差方差和已实现极差协方差

1.1 已实现极差方差

Christensen和Podolskij[13]提出了基于高频数据的已实现极差方差估计量。采用已实现极差方差来估计金融资产收益的方差，其优点在于这种方法能够充分利用高频数据的日内信息，计算简便。

其中，T为研究跨度天数，N为在[t-1,t]时间段内等时间间隔的采样次数。Δ=1/N，Δ为将[t-1,t]时间段分为N个时间段的时间间隔。 pi,t,m为金融资产i在第t日的[n-1,n]时间段内的价格。

定义1[13]已实现极差方差（Realized Range-based Variance，简称RRV）为:Christensen and Podolskij[13]证明了：

1.2 已实现极差协方差

定义2已实现极差协方差（Realized Range-based Covariance）为金融资产日内极差收益乘积之和，即

2 赋权已实现极差方差和赋权已实现极差协方差

2.1 赋权已实现极差方差

唐勇，张世英[14]在已实现极差方差的基础上，提出了赋权已实现极差方差。

定义3[14]赋权已实现极差方差（Weighted Realized Range-based Volatility,WRRV）为金融资产i的日内极差收益平方的加权之和，即

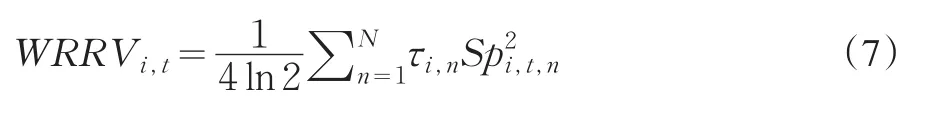
其中：τi,n为日内收益平方的权重。

从赋权已实现极差方差定义中，可以看到当τi,n=1(n=1，…，N)时，WRRVi,t=RRVi,t。即已实现极差方差是赋权已实现极差方差的一个特例。

赋权已实现极差方差中权重确定的计算公式为[14]：

赋权已实现极差方差相对于已实现极差方差具有充分考虑了“日历效应”，并且比已实现极差方差的方差更小的优点。唐勇，张世英在文献[14]中对此做出了详细阐述。

2.2 赋权已实现极差协方差

本文在已实现极差协方差的基础上，提出了赋权已实现极差协方差。

定义4赋权已实现极差协方差（Weighted Realized Range-based Covariance,WRRCOV）为金融资产i和金融资产 j的日内极差收益乘积的加权之和，即

其中，τij,n为日内极差收益乘积的权重；i,j=1,2,…。

从赋权已实现极差协方差定义中，可以看到当τij,n=1(n=1，…，N）时，WRRCOVij,t=RRCOVij,t。换句话说，已实现极差协方差是赋权已实现极差协方差的一个特例。

2.3 赋权已实现极差协方差中权重的确定

无偏性是对一个估计量最重要的要求之一，要想更好的估计金融资产收益之间的协方差，赋权已实现极差协方差首先需要满足无偏性。但是，仅仅满足无偏性是不够的。因为无偏性只能保证估计量的期望等于真值，它取的值很可能大部分与真值相差很大。因此为了保证赋权已实现极差协方差的取值能集中在金融收益之间的协方差真值附近，还需要确定一个最优的权重以使得赋权已实现极差协方差的方差最小。

（1）赋权已实现极差协方差的无偏性

设：

因

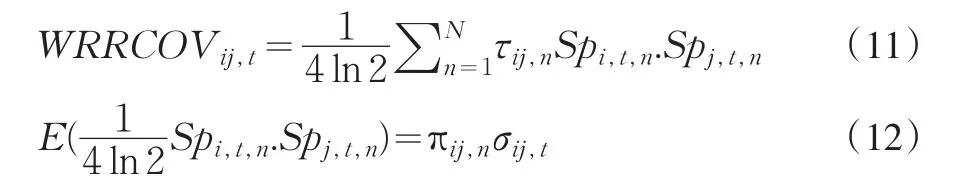
故

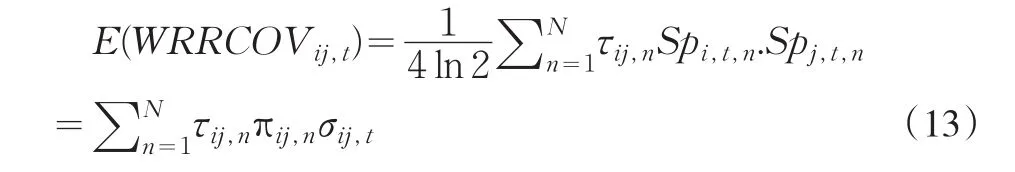
由估计量的无偏性可知，要求WRRCOVij,t满足无偏性，则下式成立：

（2）赋权已实现极差协方差的最小方差性

因

为了使WRRCOVij,t既满足无偏性，又满足最小方差性，则：

定义：

其中：θ为拉格朗日乘子。

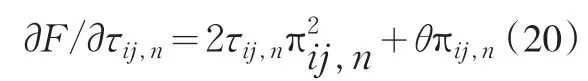
令：

故

因此赋权已实现极差协方差中权重为：

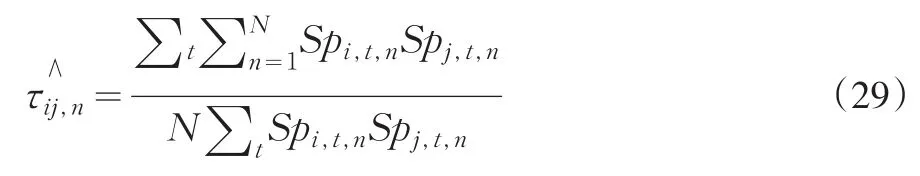
2.4 赋权已实现极差协方差相对于已实现极差协方差的优点

2.4.1 充分考虑了“日历效应”

“日历效应”是对高频金融时间序列的研究中的重要发现。所谓“日历效应”是指金融资产收益在日内表现出稳定的、周期性的运动模式，主要表现为“U”型模式。

已实现极差协方差是金融资产日内极差收益乘积之和，给每一个日内极差收益乘积都赋予了取值为1的相同的权重。但是，由于“日历效应”的存在，给不同的日内极差收益乘积赋予相同的权重显然不太合理。

而赋权已实现极差协方差是金融资产日内极差收益乘积的加权之和，它给不同的日内极差收益乘积赋予了不同的权重。也就是说，根据不同的日内极差收益乘积在日内表现的出稳定的、周期性的运动模式，相应地给每一个日内极差收益乘积都赋予了不同的权重，考虑到了“日历效应”。正因为考虑了“日历效应”，给每一个日内极差收益乘积都赋予了不同的权重，才使得赋权已实现极差协方差是既满足无偏性，又满足最小方差性的协方差估计量。

2.4.2 赋权已实现极差协方差的方差小于已实现极差协方差的方差

从赋权已实现极差协方差定义中，可以看到当τij,n=1(n=1，…，N）时，WRRCOVij,t=RRCOVij,t。也就是说已实现极差协方差是赋权已实现极差协方差的一个特例。

3 赋权已实现极差β

采用高频数据,用赋权已实现极差方差和赋权已实现极差协方差来度量市场组合收益的方差和某支股票收益与市场组合收益的协方差。由此便可以计算出赋权已实现极差β。

定义5市场组合收益的赋权已实现极差方差为

第i支股票收益与市场组合收益的赋权已实现极差协方差

第i支股票的赋权已实现系统风险系数

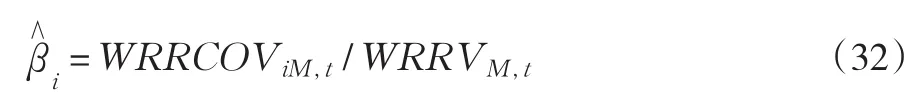
由2.1部分可知，赋权已实现极差方差和赋权已实现极差协方差充分考虑了日历效应，并且满足估计量的最小方差性。由此可见，赋权已实现极差β比采用已实现极差方差和已实现极差协方差计算的已实现极差β更精确。

4 实证分析

本文的实证研究采用的高频数据是2001-2-28～2002-4-15深证成指和晨鸣纸业、金路集团、海虹控股、冀东水泥、盐湖钾肥的30分钟间隔时段的收盘价，这期间共有269个交易日。

4.1 深证成指收益的已实现极差方差和赋权已实现极差方差的统计特征

根据式（4）和式（7），可以计算出深证成指收益的已实现极差方差和赋权已实现极差。表1给出了深证成指收益的已实现极差方差和赋权已实现极差的统计特征。

从表1中可以看到，深证成指收益的已实现极差方差和赋权已实现极差的均值相同，但是深证成指收益的赋权已实现极差的方差要小于已实现极差方差的方差。

表1 深证成指收益的已实现极差方差和赋权已实现极差的统计特征

4.2 各支股票收益与深证成指收益的已实现极差协方差和赋权已实现极差协方差的特性统计

根据式（6）和式（9），可以计算出各支股票收益与深证成指收益的已实现极差协方差和赋权已实现极差协方差。表2各支股票收益与深证成指收益的已实现极差协方差和赋权已实现极差协方差的统计特征。

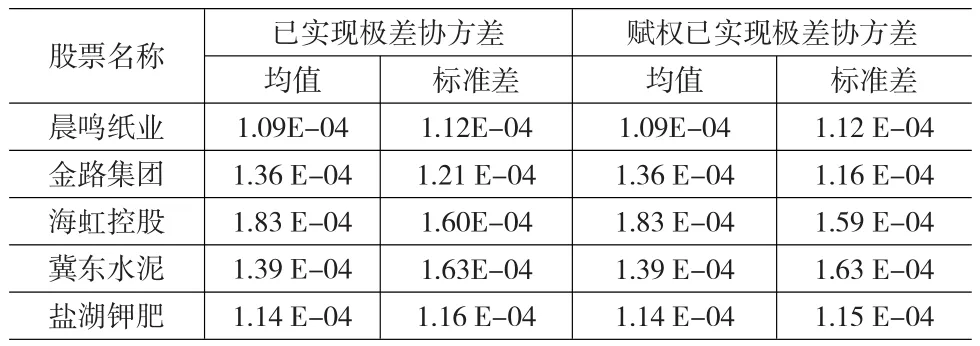
表2 各支股票收益与深证成指收益的已实现极差协方差和赋权已实现极差协方差的统计特征

从表2中可以看到，各支股票收益与深证成指收益的已实现极差协方差和赋权已实现极差协方差的均值相同，但是各支股票收益与深证成指收益的赋权已实现极差协方差的方差小于等于已实现极差协方差的方差。

4.3 各支股票的赋权已实现极差β的特性统计

表3给出了各支股票的赋权已实现极差β的特性统计结果。从表1中可以看到，各支股票的赋权已实现极差β都具有较高的偏度和峰度，其分布均不符合正态分布。

表3 各支股票的赋权已实现极差β的特性统计

5 结束语

本文采用高频金融数据，通过赋权已实现极差方差和赋权已实现极差协方差来度量市场收益的方差和股票收益与市场收益的协方差，构建了赋权已实现极差β估计量，对系统风险系数β进行了研究。实证研究证明，中国股票市场中的系统风险系数β随着时间的改变而改变具有较高的偏度和峰度，其分布均不符合正态分布。

[1] De Santis,Gerard.International Asset Pricing and Portfolio Diversifi⁃cation with Time-varying Risk[J].Journal of Finance,1997,(52).

[2] Bekaert G.,Harvey C.Time-varying World Market Integration[J].Jour⁃nal of Finance,1995,(50).

[3] Fabozzi,Frank,Francis,Clark.Stability Test for Alphas and Betas Over Bull and Bear Market Conditions[J].Journal of Finance,1977,(9).

[4] Christensen,K.,M.Podolskij.Asymptotic Theory for Range-based Es⁃timation of Integrated Variance of a Continuous Semi-martingale[R].Aarhus School of Business,2005.

[5] 唐勇,张世英.高频数据的加权已实现极差波动及其实证分析[J].系统工程,2006,24(8).