基于GARCH族模型的深证成指波动特征实证分析*

付岱山， 王 楠(沈阳工业大学 经济学院， 沈阳 110870)

股市波动性一直是众多学者研究的重点。早在1970年，Fama就发现股票价格变动具有集聚特点[1]。Engle第一次提到ARCH模型，并将其应用到实际的研究中[2]。Fama、Hageman和Lau等陆续发现收益率序列具有尖峰厚尾性等特征。1986年，Bollerslev提出了以ARCH模型为基础的GARCH模型[3]。Nelson指出GARCH模型能够解决这些问题并且效果显著。Black提出预期价格的变动对股价波动的影响是非对称性的，即股价波动具有杠杆效应[4]。对于该现象，Glosten等[5]、Zakoian[6]、Nelson等[7]提出了非对称性模型，即GJRT、ARCH和EGARCH模型。严俊宏指出我国沪市收益率具有波动性，并且受投资者情绪影响[8]。刘玄等通过GARCH族模型将样本分成两个阶段，指出沪市指数波动具有阶段性特征[9]。杨仁美等通过GARCH族模型对沪深股市进行分析，证明沪深股市波动性存在杠杆效应[10]。本文运用GARCH族模型对我国深证成指收益率的波动性进行分析。

一、指标选取及阶段划分

选取2005年5月—2017年8月的日收盘价(共3 000个)作为总体样本数据，以收益率作为研究对象，以深证成分指数价格于2007年10月最后1天达到最高点19 531.15为分界点，具体划分见表1。

表1 深证成指样本阶段划分

注：括号内数值为样本数。

以日收益率作为考察变量，计算公式为

Rt=lnPt-lnPt-1

式中：Pt为当日收盘价；Pt-1为前1日收盘价。

二、描述性统计分析

1. 深证成指基本统计特征分析

对深证成指总体及两阶段进行基本统计特征分析[11-13]，详见表2。

由表2可知，深证成指总体和两阶段的日收益率序列的均值均在0值左右。从偏度来看，深证成指3个序列的日收益率的偏度均不为0，说明深证股市收益率序列不服从正态分布。同时，深证成指3个序列的偏度均为负值，表明其分布具有左偏的特点，即深证成指日收益率小于均值的天数多。当序列呈正态分布时，其峰值应为3，但3个序列的峰度值均比3大，说明序列存在明显的“尖峰厚尾”。从J-B值来看，3个序列均显著大于临界值，P值均为0.000 0，表明序列不服从正态分布。

表2 深证成指描述性统计结果

对深证成指总体及两阶段进行时序图分析可知，深证成指总体及两阶段的序列表现出明显的波动集聚性、突发性和时变性。集聚性是金融时间序列的基本特征，说明深证成指总体及各阶段的收益率序列具有异方差性。

2. 平稳性检验

对序列进行平稳性检验，结果见表3。

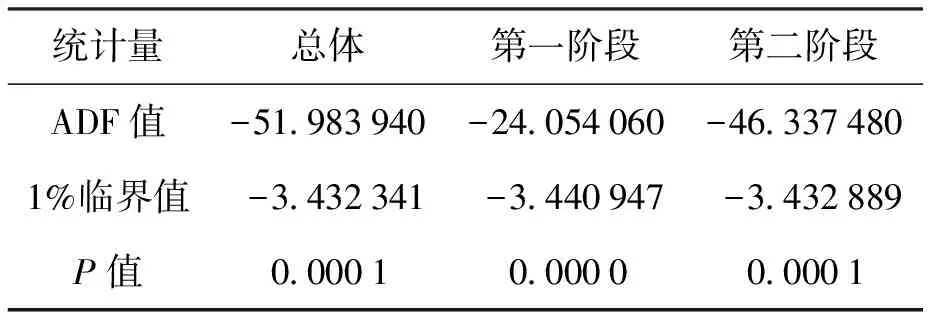
表3 序列ADF检验结果

由表3可知，深证成指日收益率序列的单位根检验值(ADF值)均远远小于1%水平下的临界值，说明在99%的显著性水平下序列是平稳的。

3. 相关性分析

对深证成指3个序列进行自相关性检验[14-15]。滞后阶数设为10，可得深证成指各阶段自相关系数(AC)与偏自相关系数(PAC)的值在0值上下，AC值与PAC值基本上都落在置信区间内，表明总体及分阶段序列不存在明显的自相关性。

4. 异方差性检验

综上可见，收益率序列具有集聚性特征，从统计角度基本说明序列具有异方差性。对序列进行ARCH效应检验，得到F统计量为25.239 56，P值为0.000 0，R2为337.561 7，说明模型显著且深证成指残差序列具有ARCH效应，即深证成指序列具有非常明显的异方差性。

三、实证分析

选取GARCH族模型中比较常用的GARCH(1，1)、TGARCH(1，1)、EGARCH(1，1)模型对深证成指总体及分阶段进行分析。

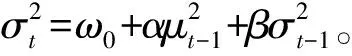
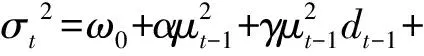
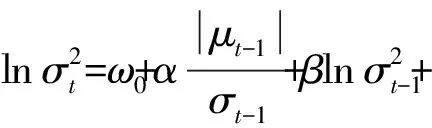
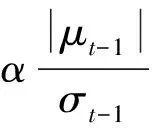
1. 深证成指总体序列建模分析

深证成指总体序列参数估计与检验结果如表4所示。

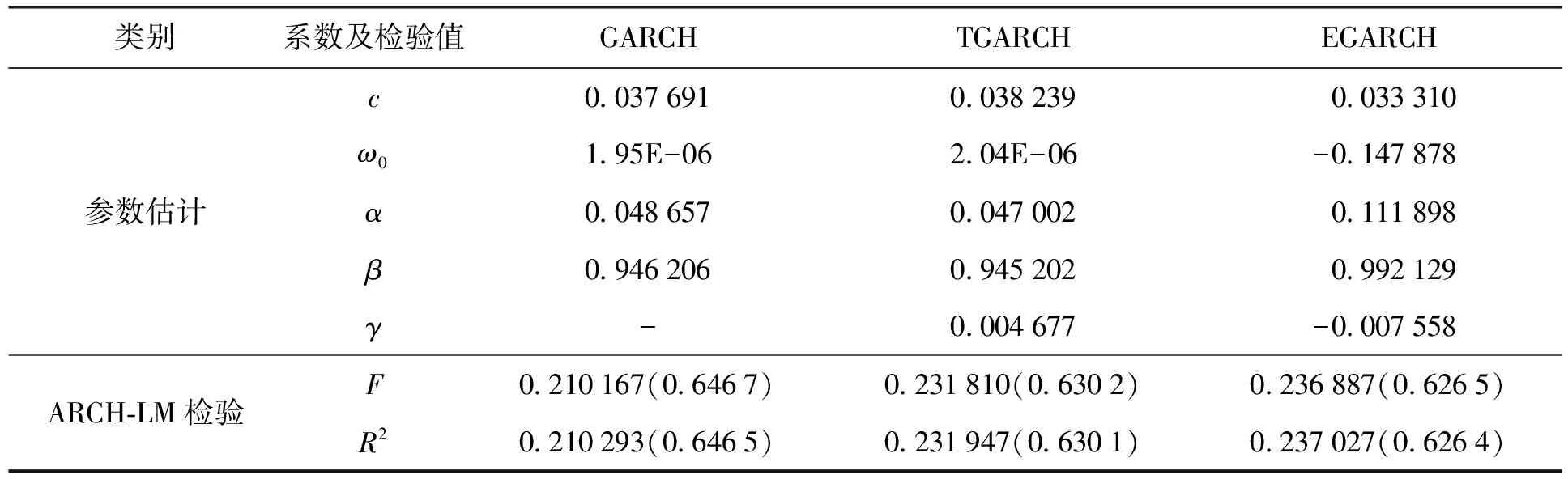
表4 深证成指总体序列GARCH族模型参数估计与检验结果

注：括号内为ARCH-LM检验的P值，下同。

(1) GARCH模型估计与分析

结果显示c项、ARCH(α)项和GARCH(β)项都很显著。从参数估计结果看，深证成指的波动持续性系数，即α与β系数之和为0.994 863<1，满足约束条件；而且该值接近于1，说明深证成指的波动受正负信息的影响会是持久并长期存在的，即外界“利好消息”或“利空消息”对深证成指价格波动的影响长期存在。并且，F=0.210 167，P=0.646 7，均显著大于0.05，方程的残差序列不存在ARCH效应，说明构建的GARCH(1，1)模型能够较好地消除原残差序列的条件异方差性。

(2) TGARCH模型估计与分析

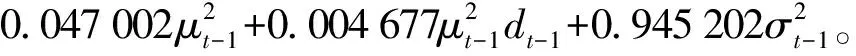
对方差方程进行分析，其非对称项系数γ=0.004 677>0，且未通过5%显著水平检验，说明深证成指总体序列的波动具有较为微弱的非对称效应；并且γ>0表示存在弱杠杆效应，即同等程度下“利空消息”给序列波动带来的冲击要略大于“利好消息”所带来的冲击。具体来说：当μt-1≥0，即出现“利好消息”时，dt-1=0，会给深证成指带来0.047 002倍的冲击；当μt-1<0，即出现“利空消息”时，dt-1=1，会给深证成指带来0.047 002+0.004 677=0.051 679倍的冲击。从检验结果可以看出，F=0.231 810和P=0.630 2，均显著大于0.05，说明方程的残差序列不具有ARCH效应，构建的TGARCH(1，1)模型能够较好地消除原序列的条件异方差性。

(3) EGARCH模型估计与分析

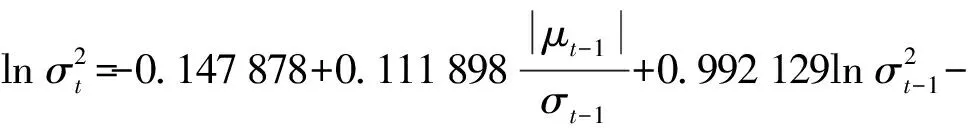
对方差方程进行分析，α=0.111 898，γ=-0.007 558<0，且未通过显著性检验，表明深证成指总体样本波动具有较为微弱的非对称性。γ<0表示存在较为微弱的杠杆效应，与TGARCH所得结论一致，即在同等程度下“利空消息”给深市收益率序列带来的冲击要略大于“利好消息”的冲击，也就是说“利空消息”影响略大。具体来说：当μt-1≥0，即出现“利好消息”时，会给深证成指带来0.111 898-0.007 558=0.104 340倍的冲击；当μt-1<0，即出现“利空消息”时，会给深证成指带来0.111 898+0.007 558=0.119 456倍的冲击。通过ARCH-LM检验可以看出，F=0.236 887，P=0.626 5，均显著大于0.05，认为EGARCH模型能够较好地消除条件异方差性。

(4) 深市总体序列结果分析

从ARCH-LM检验上来看，P值显著大于0.05，表明建立的GARCH族模型能够较好地消除残差序列的ARCH效应。

从建立的GARCH模型上看，深证成指的α+β=0.994 863<1，并接近于1，满足参数约束条件，说明深证成指的收益率波动受冲击的影响会是持续并且长期存在的，但这种效应最终会消失。

从建立的TGARCH模型上看，深证成指的非对称性系数γ>0，且没通过显著性检验，说明深证成指总体序列的股价波动具有较为微弱的非对称性，具体表现为同等程度下“利空消息”给深证成指的波动带来的影响要略大于“利好消息”。

从建立的EGARCH模型上看，深证成指的非对称性系数γ<0，且未通过显著性检验，说明深证成指的波动具有较为微弱的非对称性，显示出微弱的杠杆效应，与TGARCH模型结果一致。

2. 深证成指分阶段建模分析

对深证指数总体样本分阶段进行考察，分析各阶段的波动情况，从股市动态发展的角度来看更具有现实意义。将深证成指总体样本序列分为两个阶段，并分别建立GARCH族模型进行对比分析。

(1) 第一阶段序列GARCH族模型参数估计与分析

深证成指第一阶段序列模型参数估计与检验结果见表5。

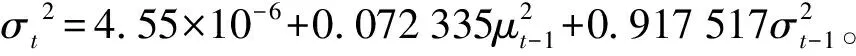
可以看出，深证成指第一阶段样本的α+β=0.989 852<1，并接近1，满足参数的约束条件，说明正负信息对深证成指第一阶段序列的影响是长期存在的，并且是收敛的。

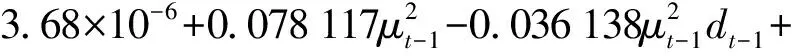
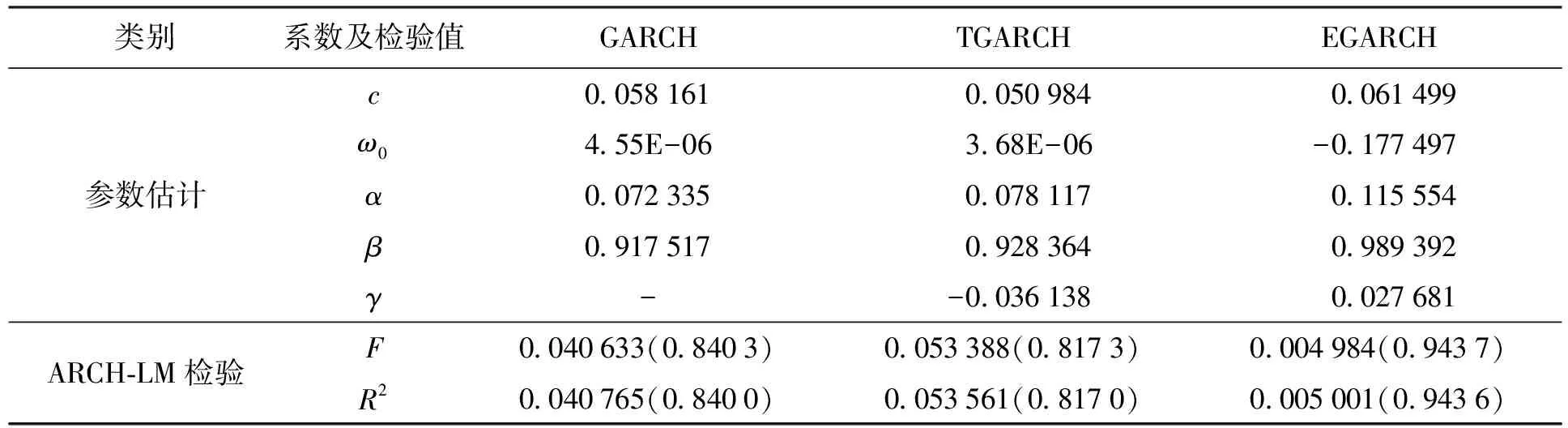
表5 深证成指第一阶段GARCH族模型参数估计与检验结果

从建立的TGARCH模型可以看出，γ=-0.036 138<0，且未通过显著性检验，说明深证成指序列该阶段的波动具有较为微弱的非对称性，而且表现为“利好消息”对第一阶段深证成指的冲击比等量“利空消息”的冲击略大一些，即为弱反杠杆效应。具体来说：当μt-1≥0，即出现“利好消息”时，dt-1=0，这一消息会给深证成指造成0.078 117倍的冲击影响；当μt-1<0，即出现“利空消息”时，dt-1=1，该消息会给深证成指带来0.078 117-0.036 138=0.041 979倍的冲击。

从建立的EGARCH模型可以看出，γ=0.027 681≠0，且通过了显著性检验，说明该序列具有非常显著的非对称性。由于γ>0，表现为“利好消息”对第一阶段深证成指的冲击要比等量“利空消息”的影响大，即为反杠杆效应。具体来说：当μt-1≥0，即出现“利好消息”时，该消息会给深证成指带来0.115 554+0.027 681=0.143 235倍的冲击；当μt-1<0，即出现“利空消息”时，会给深证成指带来0.115 554-0.027 681=0.087 873倍的冲击。

从ARCH-LM检验可以看出，第一阶段GARCH族模型的P值显著大于0.05，不存在ARCH效应，说明所构建的模型均消除了原残差序列的条件异方差性。

(2) 第二阶段序列GARCH族模型估计与分析

深证成指第二阶段序列模型参数估计与检验结果见表6。

表6 深证成指第二阶段序列GARCH族模型参数估计与检验结果

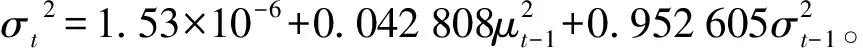
可以看出，深证成指第二阶段α+β=0.995 413<1，满足参数的约束条件，并且系数之和接近1，说明信息所带来的冲击对该阶段波动的影响将会是长期存在的，并且收敛。

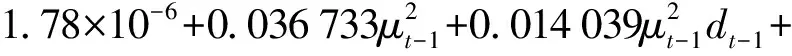
从表6可得γ=0.014 039>0，且通过了显著性检验，说明深证成指该阶段序列波动具有显著的非对称性，而且表现为“利空消息”对第二阶段深证成指的冲击比等量“利好消息”的影响大，即为杠杆效应。具体来说：当μt-1≥0，即出现“利好消息”时，dt-1=0，该消息会给深证成指造成0.036 733倍的冲击；当μt-1<0，即出现“利空消息”时，dt-1=1，该消息会给深证成指造成0.036 733+0.014 039=0.050 772倍的冲击。

从表6可知，γ=-0.017 395≠0，并且通过显著性检验，说明序列存在显著的非对称性。由于γ<0，表现为“利空消息”对第二阶段深证成指的冲击要比等量“利好消息”的影响大，即为杠杆效应，这与TGARCH模型分析结果一致。具体来说：当μt-1≥0，即出现“利好消息”时，会给深证成指造成0.102 295-0.017 395=0.084 9倍的冲击；当μt-1<0，即出现“利空消息”时，会给深证成指带来0.102 295+0.017 395=0.119 69倍的冲击。

从ARCH-LM检验可以看出，第二阶段GARCH族模型P值显著大于0.05，说明残差序列不存在ARCH效应，也就是说所建立的模型消除了原残差序列的条件异方差性。

(3) 深市分阶段结果对比与分析

从ARCH-LM检验上来看，深证成指两阶段P值都比0.05大，说明所建立的GARCH族模型都消除了残差序列的ARCH效应。

从GARCH模型上看，深证成指两阶段的α与β之和分别为0.989 852和0.995 413，两者均小于1且接近于1，满足参数约束条件，说明深证成指两阶段的波动受正负信息的冲击影响是持续的，长期存在且逐渐减弱。

从TGARCH模型上看，深证成指两阶段的非对称性系数γ≠0，且第一阶段未通过显著性检验，而第二阶段通过显著性检验，说明深市第一阶段股价波动具有较为微弱的非对称性，而第二阶段表现出显著的非对称性。第一阶段γ=-0.036 138<0，反映了在第一阶段“利好消息”对股指波动产生的冲击略大于“利空消息”的冲击，表现为弱反杠杆效应；第二阶段γ=0.014 039>0，表明“利空消息”对股价波动产生的冲击大于“利好消息”的冲击，表现为杠杆效应。这同时也体现出我国股市波动的阶段性特征。

从EGARCH模型上看，两阶段的非对称性系数γ≠0，且两阶段均通过显著性检验，说明深市两阶段的股价波动存在显著非对称性。第一阶段γ=0.027 681>0，反映了在第一阶段“利好消息”产生的冲击大于“利空消息”产生的冲击，表现为反杠杆效应；第二阶段γ=-0.017 395<0，表明“利空消息”对股价波动产生的冲击大于“利好消息”的冲击，表现为杠杆效应。这体现出我国股市波动的阶段性特征，并且与TGARCH模型所得结论一致。

TGARCH和EGARCH两个模型分析所得出结果是一致的。具体讲，深市第一阶段都反映出“利好消息”的冲击大于“利空消息”的冲击，第二阶段都反映出“利空消息”的冲击大于“利好消息”的冲击。两模型实证结果互相印证，为深市股指波动的非对称性特征提供了有力证据。

四、结 论

(1) 通过GARCH、TGARCH及EGARCH对深证成指日收益率总体及分阶段建立的模型，均有效地消除了残差序列的ARCH效应，说明GARCH族模型适用于分析我国股市波动性。

(2) 通过简单描述性统计分析，得出我国深证指数收益率波动具有集聚性的特点，即过去的股市波动会影响未来的走势；深证成指收益率序列是平稳的，不服从正态分布，并且具有“尖峰厚尾性”的结论。

(3) 我国深证成指波动具有持久性的特点，并且是收敛的；具有明显的非对称性，即“利好消息”和“利空消息”会对波动产生显著的影响。在总体序列的分析中，发现深证成指具有弱杠杆效应；第一阶段分析中，甚至显示出较为微弱的反杠杆效应；而第二阶段分析中，则显示出杠杆效应，说明我国股市波动具有一定的阶段性。此外能够看出，在进行非对称性研究时，EGARCH(1，1)模型的拟合效果更好。

[1] Fama E F.Efficient capital market：a review of theory and empirical work [J].Journal of Finance，1970，25(2)：383-417.

[2] Engle R F，Mustafa C.Implied ARCH models from options prices [J].Journal of Econometrics，1992，52(1)：289-311.

[3] Bollerslev T.Generalized autoregressive conditional heteroskedasticity [J].Journal of Econometricas，1986，24(3)：307-327.

[4] Black F.Studies in stock price volatility changes [J].American Statistical Assosiation，1976，13(1)：177-181.

[5] Glosten J R，Jagannathan R，Runkle D E.On the relation between the expected value and the volatility of the nominal ecess return on stocks [J].Journal of Finance，1992，48(4)：1779-1801.

[6] Zakoian J M.Threshold heteroskedastic model [J].Journal of Economic Dynamics and Control，1994，18(5)：931-955.

[7] Nelson T，Daniel B.Conditional heteroskedasticity in asset returns：a new approach [J].Econometrics，1991，59(2)：349-370.

[8] 严俊宏.基于投资者情绪的股市波动非对称性研究 [J].技术与市场，2013(5)：333-335.

[9] 刘玄，冯彩.2005年以来我国股票市场波动特征研究：基于GARCH族模型 [J].经济论坛，2009(2)：42-45.

[10]杨仁美，王靖.中国股票市场价格波动非对称性效应研究 [J].市场经济与价格，2010(6)：42-44.

[11]程小亮.基于GARCH模型族对上证指数波动性的实证分析 [J].商业经济，2013(7)：29-31.

[12]冷军.沪深股市指数收益率波动性的实证分析 [J].财经纵横，2012(11)：161-163.

[13]李莉，姚远.基于 GARCH 模型的深证综指指数收益率实证研究 [J].金融市场，2016(5)：52-53.

[14]严定琪，李育锋.基于GARCH族模型的沪深300指数波动率预测 [J].金融研究，2008(8)：92-95.

[15]高铁梅.计量经济学分析方法与建模 [M].北京：北京清华大学出版社，2009.