转化思想在解题中的应用例析

☉江苏省盐城市初级中学 孙 峰

化归转化思想是指运用某种手段或方法把待解决的较为生疏或复杂的问题转化为熟悉的问题来解决的思想方法.在解题实践中，大部分试题的条件与目标的联系不明显，能否根据问题的特点和解题中出现的具体情况“随机应变”，调整思路，转换策略，是我们顺利解题的一个关键因素，也是思维灵活性的一个重要体现，强化解题过程中的应变能力，有利于提高解决数学问题的思维能力和技能、技巧.化归的关键是明确化归的对象、目标和方法，化归的核心是实现问题的规范化，化归是数学解题的最基本的思想方法之一，在解题中应用十分广泛，下面举例进行说明.

例1如图1，在四边形ABCD中，已知 AB∶BC∶CD∶DA=2∶2∶3∶1，且∠B=90°，求∠DAB的度数.

解： 连接AC.因AB∶BC=1∶1，∠B=90°，所以∠BCA=∠BAC=45°，AC=AB.

设AB=2x，则AC=2x，CD=3x，DA=x.

图1

所以 DA2+AC2=x2+（2x）2=9x2，CD2=（3x）2=9x2，所以DA2+AC2=CD2，∠DAC=90°，所以∠DAB=∠DAC+∠BAC=135°.

说明：作辅助线是进行几何图形转化的常用手段，本例依据题设数据通过作辅助线实现了把不规则图形转化成规则图形（直角三角形、等腰三角形）的过程，从而求出了问题的解，这也是解几何题的一般思路，而由几何运算向代数运算的转化，可使过程简化，思路清晰.善于转化是解决一些新问题的基本要求.

图2

例2如图2，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为________.

解：本题主要考查矩形、正方形有关面积计算及观察图形、分析和解决问题的能力，转化的数学思想.通过观察发现阴影部分的面积可化为矩形面积与小正方形面积的差，因此根据条件求出小矩形的长与宽是解题的关键.易知小矩形的长与宽分别是2、.故答案为2-2.

例3如图3，A，B两地之间有一座山，汽车原来从A地到B地须经C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线 AB 行驶.已知 AC=10km，∠A=30°，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据：≈1.41，≈1.73）

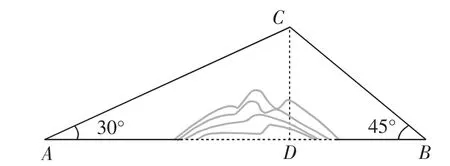
图3

分析：已知图形是一个斜三角形，要求其解，可以通过作高线的方法，将其斜三角形转化成直角三角形，这样就便于运用锐角三角形函数的知识求解.

解：过点C作CD⊥AB，垂足为D.在Rt△CAD中，因为AC=10km，∠A=30°，

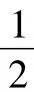
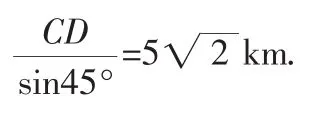
AB=AD+BD=（5+5）km，

≈5+5×1.41-5×1.73≈3.4.

大肠杆菌的基本特征：肠埃希氏菌通常称为大肠杆菌，是 Escherich在1886年发现的，在相当长的一段时间内，一直被当做正常肠道菌群的组成部分，认为是非致病菌。直到20世纪中叶，才认识到一些特殊血清型的大肠杆菌对人和动物有病原性，尤其对婴儿和幼畜（禽），常引起严重腹泻和败血症。

所以隧道开通后，汽车从A地到B地比原来少走约3.4km.

说明：在解题时，常把有待解决或难以解决的问题通过某种转化手段，使它转化成已经解决和比较容易解决的问题，从而求得原问题的解答，这种转化思想不止用于解方程的换元，在解几何证明及解综合题也经常用到，本题就是最好地说明.

例4解方程2（x-1）2-5（x-1）+2=0.

解：令 y=x-1，则2y2-5y+2=0.

例5如图4，四边形ABCD是一矩形，E是AB上一点，且BE∶EA=5 ∶3，EC=15，把△BCE沿折痕EC向上翻折，若点B恰好落在AD边上，设这个点是F，以点A为原点，以直线AD为x轴，建立直角坐标系，求直线FC的解析式.

解：沿EC把△BCE向上翻折，点B落在点F，故△BCE≌△FCE，所以BE=FE，BC=FC.设EA=3t（t＞0）.因BE∶EA=5∶3，所以BE=5t，EF=5t.在 Rt△AEF中，可得AF=4t.所以E（0，-3t），B（0，-8t），F（4t，0）.设BC=a，则点C的坐标为（a，-8t）.在 Rt△BCE中，BC2+BE2=EC2.所以a2+25t2=（15）2.

图4

在 Rt△BCE与 Rt△DFC中，因∠1+∠2=90°，∠3+∠2=90°，所以∠1=∠3.

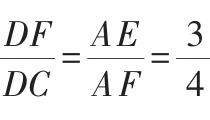
所以F（12，0），C（30，-24）.

设图像经过点F、点C的一次函数解析式是y=kx+b.

说明：本题的解题过程可以概括为三个转化.首先，把条件叙述的几何操作性语言通过空间想象转化为图形位置关系，正确画出图形，这是解此题的基础；第二，通过“设t”把“比”转化为长度，再数形结合把长度转化为点的坐标；第三，恰当地把图形分解为相互关联的“基本图形”，把位置关系转化为数量关系，最后通过反映数量关系的方程实现未知向已知的转化.