构建数学模型培养解题能力

☉江苏省赣榆县塔山中学 瞿世彩

把实际问题转化为一个数学问题，通常称为数学模型.提高中学数学教学质量，最重要的是学生学到有用的数学，构建数学模型也是中学数学教学改革的方向.自实施新课标以来，以物理、化学、生物、医学等学科知识为背景的跨学科综合题颇受关注.有些问题用常规方法难以解决，往往需要构建一个与之有关的数学模型.建立数学模型的过程称为数学建模.数学建模就是要把现实生活中具体实体所包含的数学知识、数学规律抽象出来，构成数学模型，根据数学规律进行推理求解，得出数学上的结论返回解释验证，以求得实际问题的合理解决.本文结合几道中考题，谈谈几种数学模型的构建.

一、构建方程模型

在数学教学中，将生产与生活中的实际问题数学化，建立数学模型，培养学生应用数学的意识，让学生在数学建模的过程中体会到数学的工具性作用，激发学生学习数学的兴趣和积极性.

例1读诗词解题

大江东去浪淘尽，千古风流人物；而立之年督东吴，早逝英年两位数.

十位恰小个位三，个位平方与寿符；哪位学子算得快，多少年华属周瑜？

解析：命题者借用苏轼诗词《念奴娇赤壁怀古》的头两句，烘托出“面对兴盛的江山，追忆古人勋业”的意境，强调对古文化的阅读理解，贯通数学的应用，激发学子的孜孜以求，报效国家的志气，在素质教育的背景下，不失是一道有所创新的好试题.解答时，需要透彻地分析实际问题中已知量与未知量间的关系，将问题中自然表达的实际问题转化为数学符号表示的方程，建立方程模型，通过解方程来解决实际问题.把实际问题周瑜去世时的年龄抽象为数学问题求两位数问题，建立方程的数学模型.可设周瑜去世时的年龄的个位数字为x，则十位数字为x-3，由题意得x2=10（x-3）+x，即x2-11x+30=0，解得x1=5，x2=6.当x=5时，周瑜去世时的年龄为25岁，而非而立之年，不合题意，舍去.当x=6时，周瑜年龄为36岁，完全符合题意.则周瑜去世时的年龄为36岁.

二、构建函数模型

函数反映了事物间的广泛联系，揭示了现实世界众多的数量关系及变化规律.函数的最大特点是数形结合，函数图像将方程、不等式、几何等知识融为一体.有些问题可考虑构建函数模型来解，数形结合，既直观又简单.

例2（2001年山西省）某商场计划投入一笔资金采购一批紧俏商品，经过市场调查发现，如果月初出售，可获利15%，并可用本和利再投资其他商品，到月末又可获利10%；如果月末出售可获利30%，但要付出仓储费用700元.请问：根据商场的资金状况，如何购销获利较多？

解：设商场投入的资金为x元，到月末时的盈利数为y元.

如果月初出售，那么到月末盈利数为y1=［（1+15%）（1+10%）-1］x=0.265x；

如果月末出售，那么盈利数为y2=30%·x-700=0.3x-700.

则y1-y2=-0.035x+700=0.035（20000-x）.

当0＜x＜20000时，y1-y2＞0，即y1＞y2，此时月初出售获利较多；

当x=20000时，y1=y2，月初出售和月末出售获利一样多；

当x＞20000时，y1＜y2，月末出售获利较多.

利用一次函数的单调性解题，在中考数学应用题的新变化中出现最多，它不同于单纯的一次函数，其自变量的取值范围往往有较多的限制条件.同时，在运用一次函数的性质解决问题时，还往往涉及到分类思想.这是中考数学应用题的热点.

三、构建几何图形模型

几何与人类生活经验和实际需要密切相关.根据已知条件，添加适当的辅助线，构造出恰当的几何图形，如直角三角形、全等三角形、正方形、圆、轴对称图形等，利用这些特殊图形的性质，解决问题，往往能化难为易，事半功倍.

例3（2006年河北省）图1是某学校存放学生自行车的车棚的示意图（尺寸如图1所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形.图2是车棚顶部截面的示意图，AB所在圆的圆心为O.车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结果保留π）.

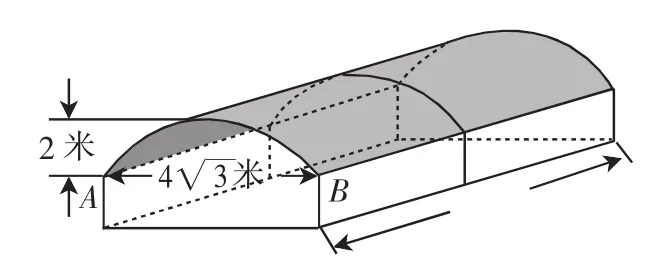
图1

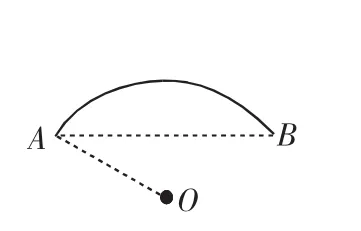
图2

解：连接OB，过点O作OE⊥AB，垂足为E，交弧AB于F，如图3.

由垂径定理，可知E是AB的中点，F是弧AB的中点，

所以EF是弓形的高.

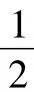
设半径为R米，则OE=（R-2）米.

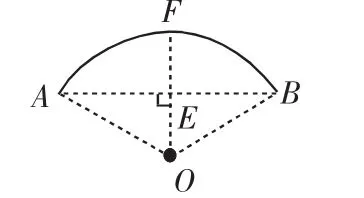
图3

在Rt△AOE中，由勾股定理，得R2=（R-2）2+（2）2，解得R=4.

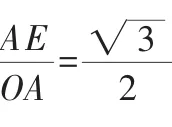
学生的建模能力的获得不是一朝一夕的事情，需要把数学模型意识贯穿到数学的始终，也就是要不断地引导学生用数学思维的观点去观察、分析和表示各种事物关系、空间关系和数学信息，从纷繁复杂的具体问题中抽象出我们熟悉的数学模型，进而达到用数学模型来解决实际问题，是数学建模意识成为学生思考问题的方法和习惯.

1.周南照，等.学会求知.北京：北京出版社，1999.

2.赞可夫和教师的谈话.北京：北京教育科学出版社.

3.王迎东，张大英.从常见应用性问题看数学模型.1997.