架通领域沟壑 拓展知识应用：以平均数的拾级拓展应用为例

☉山东省栖霞市庙后中学 王忠刚

☉山东省栖霞市教体局教研室 王志进

《课程标准（2011年版）》将数学课程内容分为数与代数、图形与几何、统计与概率、综合与实践四个领域，笔者认为这四部分内容是一个不可分割的有机整体，是一个经过精心设计和系统规划的课程内容体系，而且这样的课程内容划分也是因为领域课程内容的目标及教学要求相同，方便学生整体、系统、模块化的学习.

但是，在新课标的实施过程中，有的教师没有理解课程内容划分的本意，人为地割裂了四大领域之间的内在联系，在四大领域之间挖掘出巨大的鸿沟，从而窄化了知识的应用.

本文以统计领域中的一个重要的统计量——平均数为例，说明平均数在数与代数领域的广泛应用.

首先，由于平均数的计算公式是用代数式来表示的，这就为实现平均数的跨领域应用提供了基本的条件.

其次，平均数是描述数据集中程度的一个统计量，所有数据在平均数上下波动，并且它们与平均数之间都存在着偏差；偏差有正有负、有大有小，偏差之和等于0.偏差的这些特点为我们提供了解题契机：通过引进波动参数，利用偏差的正负，转换解题思路，发现解题途径.

巧借平均数设参妙解题的应用可分为三个拾级拓展的层次：结构明显，套着用；直用受阻，变着用；结构隐晦，挖着用.

下面，我们举例说明其应用.

第一层次：结构明显，套着用

如果已知条件中含有几个数（或字母）的和的结构特征，我们很容易联想到平均数的知识，我们就可以直接套用平均数的知识解题.

例1已知b+c=8，bc=a2－12a+52，求证：b=c=4.

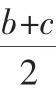
设b=4+t，c=4－t，代入bc=a2－12a+52，得：

a2－12a+t2+36=0.

因Δ=144－4（t2+36）=－4t2≥0，得t=0.

所以b=c=4.

评注：根据和的结构特点，我们巧妙地假设参数，为代数式等式的证明提供了新颖别致的解法.

例2已知实数a、b、c为实数，且a+b=8，c2+16=ab，求a+2b+3c的值.

故可设a=4+t，b=4－t，代入c2+16=ab，得：

c2+16=（4+t）（4－t），即c2+t2=0，解得c=0且t=0.

所以a=4，b=4.

故a+2b+3c=4+2×4+3×0=12.

例3 已知x+y+z=3a（a≠0），求代数式：

令x=a+t1，y=a+t2，z=a+t3且t1+t2+t3=0.

所以t1=a+x，t2=a+y，t3=a+z.

由t1+t2+t3=0，得t1+t2+t3+2（t1t2+t2t3+t1t3）=0.

评注：上述两个例题含有几个数（或字母）的和的结构特征，我们很容易想到平均数公式，巧借平均数设参妙解.

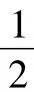
评注：本题的证法比较多，但是借助平均数的方法巧设参数，解法特别简单，其原因就是创造出正负项相互抵消.

第二层次：直用受阻变着用

如果题目中含有几个数（或字母）的和的结构特征，但是不能直接使用平均数的知识解决问题时，我们可根据解题的需要，把已知条件变形后再用.

例5若a+b+c=0，a3+b3+c3=0，求a2011+b2011+c2011的值.

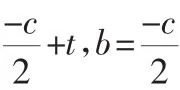
若c=0，则a=－b，有a2011+b2011+c2011=0；

评注：上述例题虽然含有几个数（或字母）的和的结构特征，但是我们不能直接借用平均数公式解题，因此，我们需要把已知条件直接变形后巧借平均数设参，然后找到a、b、c之间的关系，顺利求解.

例6设a+b+c+d+e=8，a2+b2+c2+d2+e2=16，求e的最大值.

解：由a+b+c+d+e=8，得a+b+c+d=8-e，

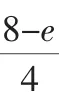
评注：由于我们不能直接使用平均数公式解题，但我们看到结论要求的最大值，因此，我们把已知条件直接变形后巧借平均数设参，然后构造了关于e的不等式，解关于e的不等式求得最值.

第三层次：结构隐晦挖着用

如果题目中不含有几个数（或字母）的和的结构特征，当然我们不能直接使用平均数的知识解决问题，这时候我们要仔细审题、灵活变形，挖掘题中隐含的、可利用的解题信息，人为地构造平均数的知识解题.

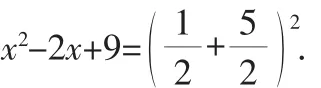
解得x=0或x=2.

评注：本题初看与平均数的关系不大，但是我们依然可以把“－”转化为“＋”，创造机会使用平均数来求解.

例8分解因式：（6x+7）（23x+4）（x+1）-6.

即（6x+7）、（6x+7）、（6x+8）、（6x+6）的平均数为（6x+7）.

故可设y=6x+7，

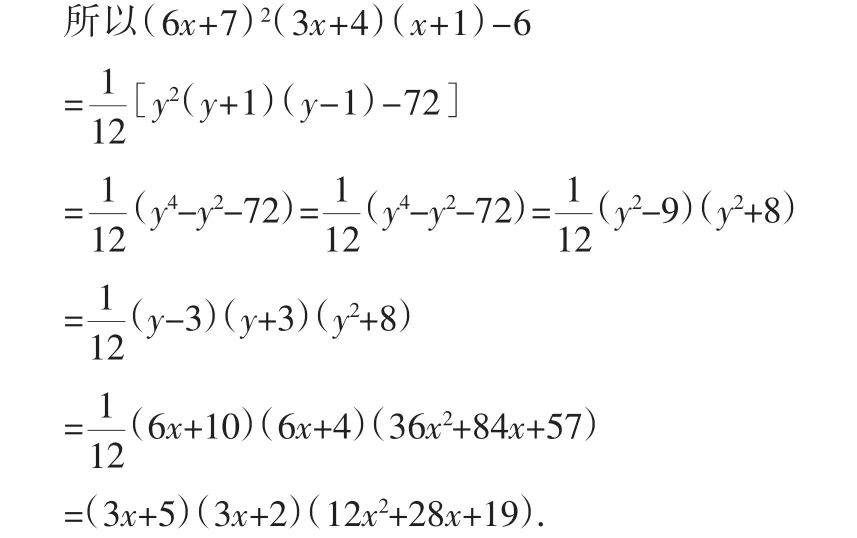
评注：本题没有明显的和的结构特点，但是，我们仍然使用平均数的方法试一试，机会顿出，立即达到高次方程低次化、陌生问题熟悉化的化归功能.

例9解方程（x+3）4+（x+1）4=82.

设y=x+2，故原方程变为（y+1）4+（y-1）4=82.

即y4+6y2-40=0.

解得y2=4或y2=-10（舍去）.

所以y=2或y=-2.

所以x+2=2或x+2=-2.

解得x=0或x=-4.

例10计算：992-103×97.

所以992-（100+3）×（100-3）

=992-1002+9

=（99-100）（99+100）+9

=-190.

评注：本题是有关具体的实数运算的题目，它没有代数式运算的显性特征，因此利用构造平均数来简化运算就更具难度.但是，我们只要仔细观察题中的三个重要数据：103，99，97，我们还是容易想到取这三个数的中间数，这个工作自然是由平均数来完成的，从而利用平均数构造平方差公式来简化运算.

我们通过10个例题说明了平均数思想在数与代数领域即求代数式的值、证明代数式等式、因式分解、解方程、证明不等式、求最值等六个方面的广泛应用，其解题方法新颖别致，解题过程简单明了，给人耳目一新的感觉，既沟通了知识之间的联系，拓展了知识的应用，深化了对知识的理解，又提高了数学素养.