基于GA-RBF神经网络逆的两电机同步控制

康 梅，赵文祥，吉敬华，刘国海

(江苏大学，江苏镇江212013)

0引 言

随着多电机变频调速系统在造纸、电动汽车、轨道交通等领域越来越广泛的应用，高性能的同步协调控制成为亟待解决的技术难题。国内外学者对多电机系统中速度和张力的解耦控制进行了一系列的研究［1-4］。其中，将逆系统与神经网络相结合的神经网络逆系统方法［5-8］，从控制算法入手，结合两者优势，实现了对一般非线性系统的线性化和解耦控制，最近几年来成为提升被控系统控制性能的一种新方法。但已有在训练神经网络时，存在着收敛速度慢、甚至会造成网络发散，且不易得到全局最优值以及结构和类型的选择过分依赖经验等缺陷。系统输入输出之间映射关系不能很好地被反映，大大降低网络的逼近性能。本文结合径向基函数(Radial Basis Function，RBF)神经网络［9-10］和遗传算法(Genetic Algorithm，GA)的思想［11-12］，提出一种基于遗传算法优化的RBF神经网络逆系统的两电机同步控制方法。遗传算法是模仿生物遗传学和自然选择机理，通过人工方式构造的一类优化搜索算法。遗传算法具有鲁棒性强、搜索范围广、搜索效率高的特点。运用遗传算法训练RBF神经网络无需先验知识，对初始参数不敏感，不会陷入局部极小点。实验证明该方法能实现两电机速度和张力的解耦控制，而且有实时性好，响应速度快，鲁棒性强等优点。

1两电机同步系统的可逆性问题

图1为速度和张力控制的两电机同步系统物理模型。

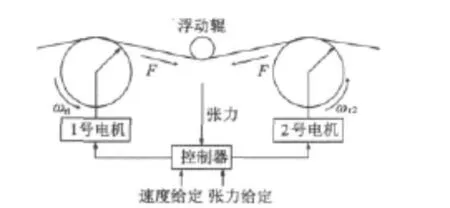
图1 两电机同步控制示意图

根据力学弹性理论中的胡克定律，张力如下:

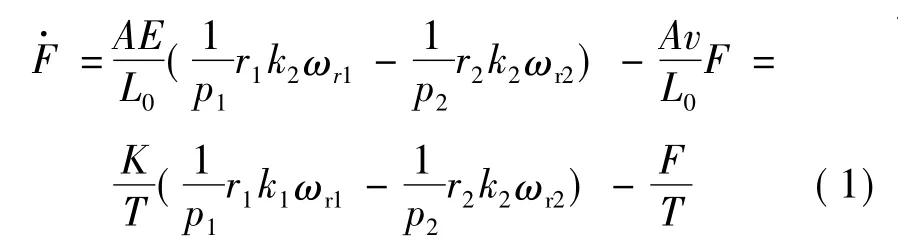
变频器采用矢量控制方式，忽略变频器的电流滞后时间常数，两电机同步系统的模型简化:

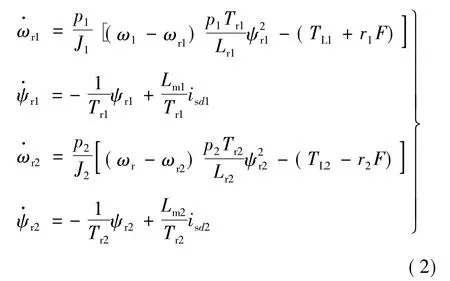
式中:F为皮带之间的张力;A为皮带的截面积;r为电机皮带轮半径;k为皮带轮速比;K为传递系数;T为张力变化常数;ωr为转子速度;p为电机极对数;v为期望的转速;E为皮带的弹性杨氏模量;L0为两电机支架间的距离;ω为电机同步角速度;ψr为转子磁链;J为转动惯量;TL为负载转矩;Tr为电机时间常数;Lr为转子电感;Lm为转子和定子间的互感。式中下标的1，2代表第1，2台电机。

对于式(1)、式(2)中的电机模型而言，其磁通子系统是线性的，在不考虑磁通变化的情况下，可将其改成为:

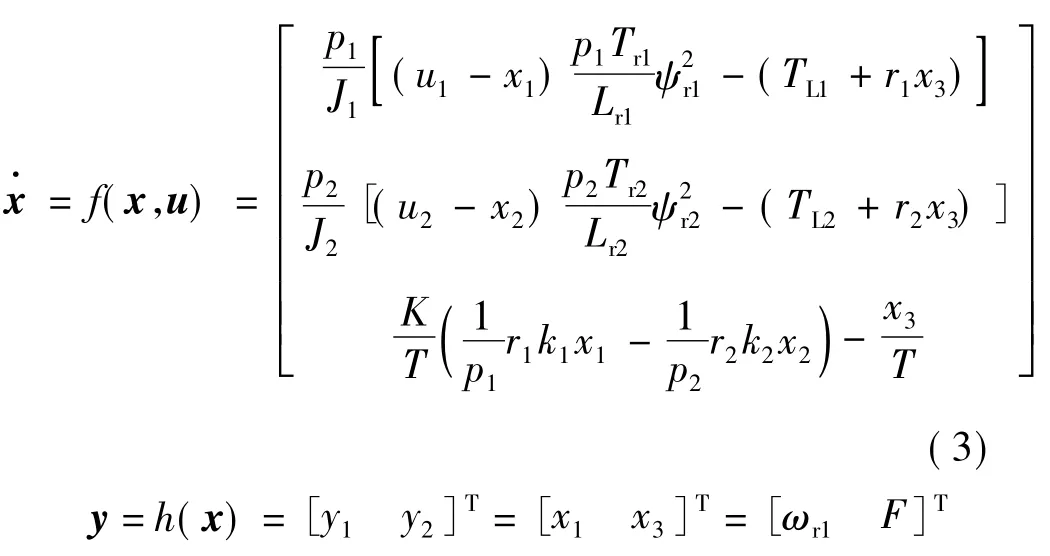
式(3)状态变量:

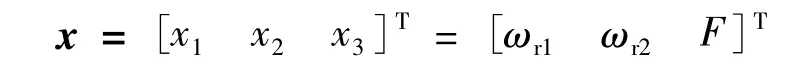
控制变量:

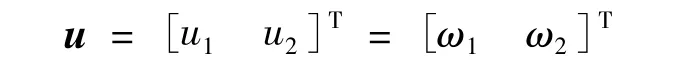
对输出求导后，得:

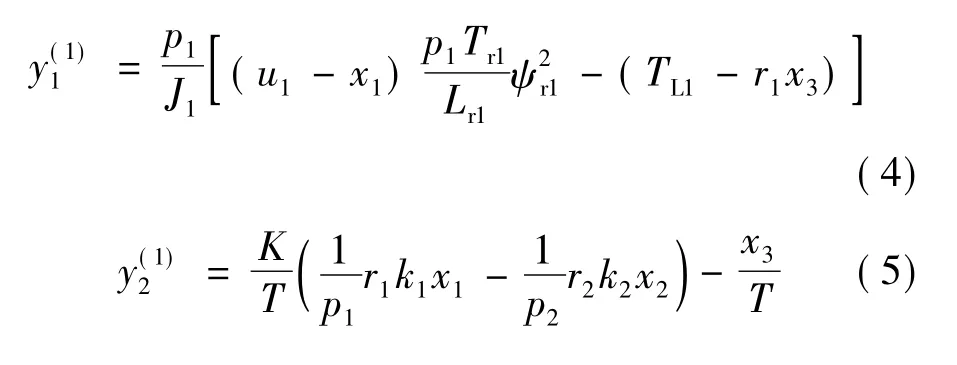
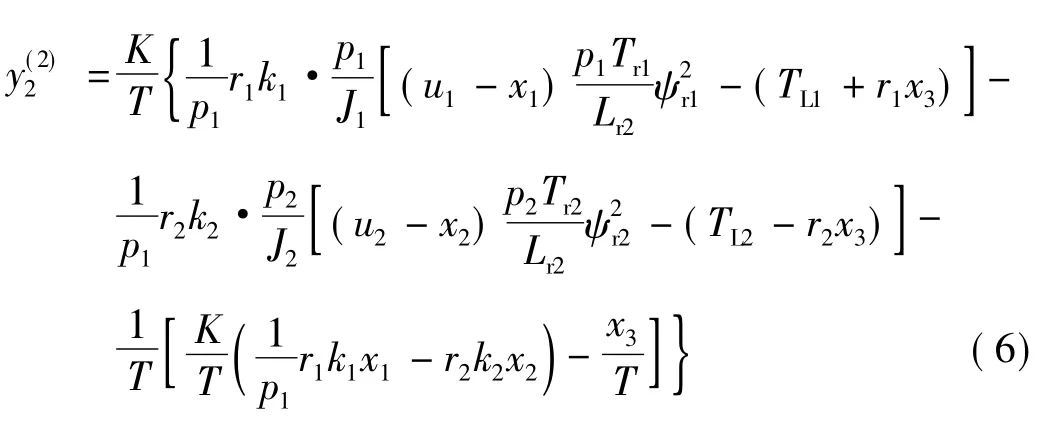
则Jacobi矩阵:

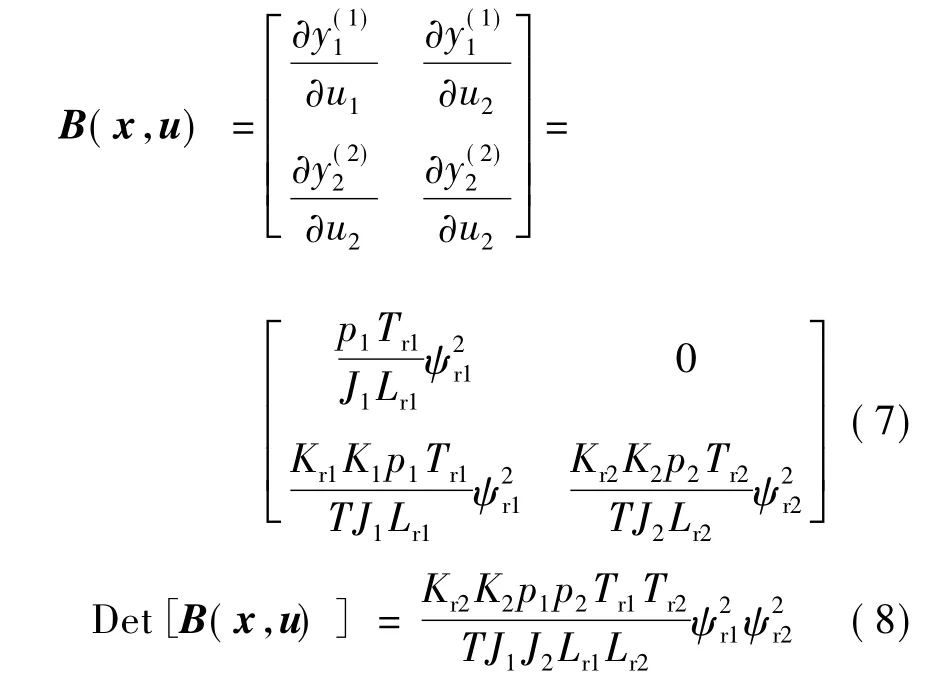
当 ψr1与 ψr2均不为零时，B(x，u)的行列式亦非零，即为非奇异矩阵。系统的相对阶数为∂=(1，2)，即∂1+∂2=3＜n。因此可知，此两电机同步系统可逆。复合被控系统由被控系统与两电机同步系统相串联构成，此时被控系统是线性的，且被解耦成速度和张力两个独立的子系统。

2 GA-RBF神经网络逆控制

神经网络具有强大的自学习能力，只要隐层和隐层节点数足够多，就可以实现任意从输入到输出的非线性映射。目前，BP网络在神经网络算法中用的比较广泛，但BP网络在逼近能力、分类能力和学习速度等方面均逊于RBF网络，所以本文采用RBF网络。鉴于神经网络易陷入局部最小、全局搜索能力弱等缺点，遗传算法具有高效全局寻优能力，本文将神经网络和遗传算法两者相结合，构成了GARBF神经网络。

2．1 RBF神经网络结构

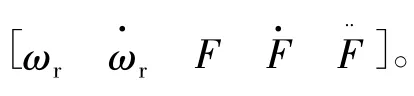
RBF神经网络采用输入层、隐含层、输出层三层结构，节点数依次为 5，7，2。设 X=［x1，x2，x3，x4，x5］，X 为网络的输入向量。

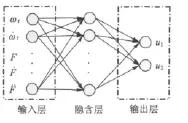
图2 RBF神经网络结构

其中RBF的隐含层采用通用的高斯函数:

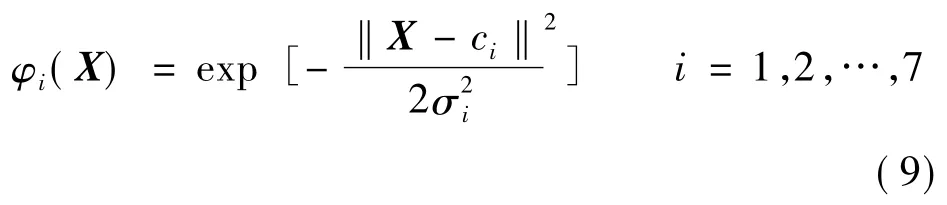
式中:ci为第i个隐层节点的中心;σi为第i个隐层节点的宽度。网络输出:

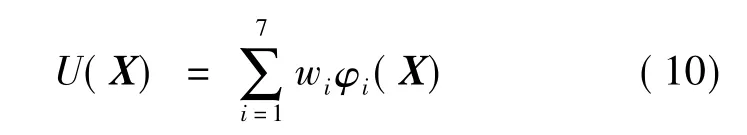
式中:wi为第i个隐层节点与输出空间的连接权。

由以上分析可知，在RBF网络中，需要确定的参数主要有隐含层的中心ci和宽度σi以及隐含层与输出层之间的连接权值wi，这三个参数的取值影响着RBF神经网络性能的好坏。因此必须选择合适的 ci、σi、wi，以提高 RBF 网络性能。

2．2遗传算法(GA)对RBF网络的优化

用于RBF网络的学习算法有很多，但都存在一定的局限性。相比而言，在所有算法中，最有效的方法是遗传算法。遗传算法是模拟生物进化论的自然选择和遗传学机理的生物进化过程的计算模型。是一种通过模拟自然进化过程搜索全局最优解的方法。特点是直接对结构对象进行操作，不需要确定的规则和其他辅助信息，就能搜索到最优参数［13］。本文采用GA遗传算法的群体并行搜索和全局收敛最优的能力，对RBF神经网络的隐层中心值、宽度值以及和输出层之间的权值进行优化。

(1)染色体编码

为了便于操作和提高精度，本文直接采用实数编码，而未采用传统的二进制形式编码。待优化的RBF神经网络的每个参数用一个实数来表示，参数个数的总和即为码串的长度。编码时，先顺序排列不同的中心值以及与之对应的宽度，再将各个调节权重值顺序排列。在重要算子的交叉作用下，同一个体的中心值以及与之对应的宽度值同时变化的概率较高，容易实现宽度值随着中心值的变化而变化的要求。对5个输入量、7个隐层节点、2个输出量的RBF神经网络，径向基函数隐层节点的中心参数、宽度参数以及隐层节点与输出空间连接权组成的编码串如下:c11，…，c15;c21，…，c25;…;c71，…，c75;σ1，…，σ7;w11，w21，…，w71;w12，w22，…，w72共 56 个参数(串长=56)。

(2)产生初始种群

M个染色体串随机产生，其取值一般介于50～100之间，本文中初始种群取为80。

(3)适应度函数的选取

遗传算法在进化搜索中只以适应度函数为依据，很少利用其他信息。因而适应度函数的选取与遗传算法的收敛速度以及与能否找到最优解密切相关。

为了能够比较直观地反映每个染色体性能的好与差，选取RBF网络的期望输出与实际输出之差的绝对值的累加和的倒数作为适应度函数［14］。即对第i个染色体，其适应度:

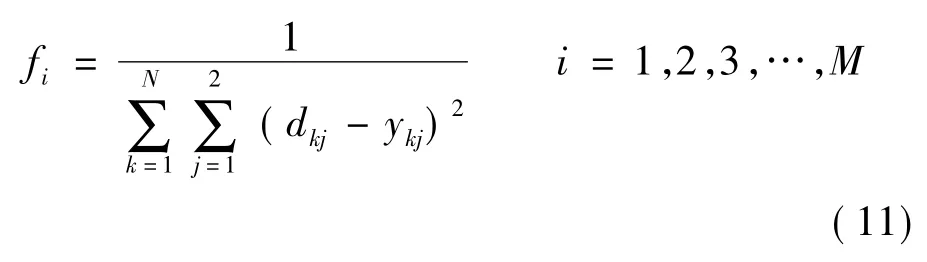
式中:N为训练样本量;ykj为训练样本的输出实际值;dkj为训练样本输出的期望值;M为染色体串的初始种群值。fi与适应度呈正相关关系。

(4)选择操作

依据适应度比例的方法，个体选择的概率正比于适应度值大小，即:

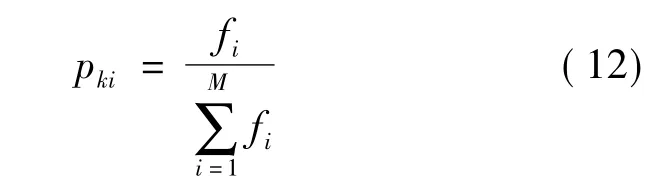
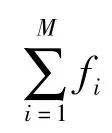
(5)自适应变异和交叉操作

本文采取按位变异的方法进行变异操作，两点交叉法进行交叉操作［15-16］，为保持种群的多样性，取变异和交叉的概率分别为pm和pc，如下式:

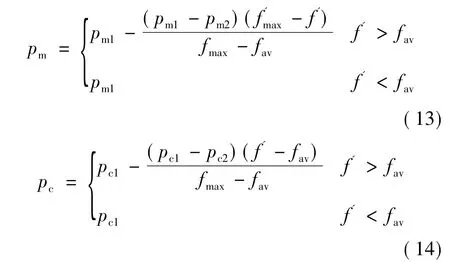
式中:f'为两个待交叉的个体中适应度较大的值;f为变异个体的适应度值;fmax为群体中适应度最大值;fav为每代群体的适应度平均值。

2．3神经网络逆系统的实现

用MATLAB软件构造神经网络，使用输入输出样本约6000组数据训练神经网络，由于篇幅有限，略去具体值。将误差指标设在0．001。在遗传算法优化网络参数中，群体初始大小为80，pc=0．6，pm=0．02，来获得RBF神经网络的最优控制参数。

将训练好的RBF神经网络逆系统，串在两电机同步系统之前，构成复合被控系统。此时被控系统被解耦成两个相对独立的伪线性子系统。y=s-1·φ(s)为伪线性速度子系统，y=s-2φ(s)为伪线性张力子系统。设计PI调节器整定速度伪线性子系统，设计PD调节器整定张力伪线性子系统，图3为神经网络逆系统控制的两电机控制系统结构示意图。

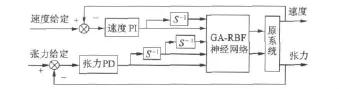
图3 控制系统结构示意图

3实验验证

为验证理论分析的正确性，搭建了多电机实验系统，如图4所示。实验系统中笼型电机型号Y100L1-4，额定转速1 420 r/min，额定功率2．2 kW，线电压380 V，星型接法。硬件由西门子MMV变频器、光电编码器、12位高速模数转换器—ADC7112、24位高速计数卡—PCL833以及与变频器RS485接口连接的串行通讯卡—PCL745组成。运用C++编写数据采样程序与通讯程序，采用USS协议进行通讯。

在两电机实验系统上，变频器工作在矢量控制方式状态，验证了神经网络逆系统方法的控制效果。图5是张力给定保持不变，对速度给定突加，采用GA-RBF神经网络控制器的张力和速度响应曲线。图6为速度给定保持不变，对张力给定突加，采用GA-RBF神经网络控制器的张力和速度响应曲线。

图4 多电机试验系统

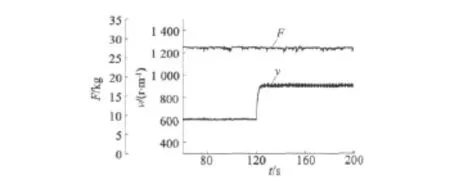
图5 GA-RBF神经网络控制速度突加张力恒定响应图

上述实验结果验证了GA-RBF神经网络控制下的速度与张力的解耦效果。速度和张力在突变情况下，均未明显影响对方的控制效果，满足了两电机系统的速度、张力解耦控制要求，系统的抗干扰性和鲁棒性得到明显提升。

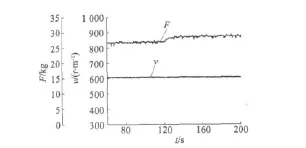
图6 GA-RBF神经网络控制张力突加速度恒定响应图

4结 语

本文提出了一种新型GA-RBF神经网络逆控制方法，用以解决神经网络逆系统方法在实际应用时逆模型难以求取等问题。该方法兼具遗传算法和RBF网络的双重优点。遗传算法具有自组织性、自适应性和智能性，可以解决一些复杂的非线性问题。RBF网络的学习速度快，能更好达到实时控制，避免了BP网络容易局部极小的问题。将两电机调速系统作为控制对象，进行了实验验证，证明了理论分析的正确性。

［1］ Michael C A，Safacas A N．Dynamic and vibration analysis of a multimotor DC drive system with elastic shafts driving a tissue paper machine［J］．IEEE Transactions on Industrial Electronics，2007，54(4):2033-2046．

［2］ Abjadi N R，Soltani J，Askari J，et al．Nonlinear sliding-mode control of a multi-motor web-winding system without tension sensor［J］．IET Control Theory ＆ Applications，2009，3(4):419-427．

［3］ Kim J，Park C，Hwang S，et al．Control algorithm for an independent motor-drive vehicle［J］．IEEE Transactions on Vehicular Technology，2010，59(7):3213-3222．

［4］ Ben M W，Belhadj J，Pietrzak-David M．Sliding mode observer for mono-inverter bi-motors railway traction system［C］//8th International Multi-Conference on Systems，Signals and Devices(SSD)．2011:1-6．

［5］ Yu D C，Liu F，Lai P Y，et al．Nonlinear dynamic compensation of sensors using inverse-model-based neural network ［J］．IEEE Transactions on Instrumentation and Measurement，2008，57(10):2364-2376．

［6］ 戴先中，刘国海，张兴华．交流传动神经网络逆控制［M］．北京:机械工业出版社，2007．

［7］ Zhao Xinlong，Tan Yonghong．Modeling hysteresis and its inverse model using neural networks based on expanded input space method［J］．IEEE Transactions on Control Systems Technology，2008，16(3):484-490．

［8］ 孙玉坤，任元，黄永红．磁悬浮开关磁阻电机悬浮力与旋转力的神经网络逆解耦控制［J］．中国电机工程学报，2008，28(9):81-85．

［9］ 宣光银，胡丹，车畅．基于RBF神经网络的SVPWM研究［J］．微特电机，2011(9):45-47．

［10］ 夏轩，许伟明．改进的粒子算法对RBF神经网络的优化［J］．计算机工程与应用，2012，48(5):37-40．

［11］ 刘金琨．智能控制［M］．北京:电子工业出版社，2005．

［12］ 王广生，黄守道，高剑．改进遗传算法在永磁电动机优化设计中的应用［J］．微特电机，2011(7):9-12．

［13］ 张明君，张化光．遗传算法优化的RBF神经网络控制器［J］．电机与控制学报，2007，11(2):183-187．

［14］ Pehlivanoglu Y V，Baysal O．Vibrational genetic algorithm enhanced with fuzzy logic and neural network［J］．Aerospace Scienceand Technology，2010，14(1):56-64．

［15］ 廖本先，杨宜民，张学习．自适应遗传算法和RBF网络在传球中的应用［J］．计算机仿真，2010，27(9):169-172．

［16］ 赵海波．基于改进遗传RBF神经网络的双电机驱动伺服系统控制［J］．井冈山大学学报，2011，32(4):76-80．