基于模型预测前馈的滚转稳定伺服系统控制研究

2012-07-23许叙遥

微特电机 2012年8期

许叙遥，林辉

(西北工业大学院，陕西西安710072)

0引言

滚转稳定平台是一种降低载体本身的滚转角运动对其负载影响稳定装置，主要应用于火箭弹、迫击弹、巡航导弹上，用来搭载导航和制导设备。根据稳定方式不同，包括动力陀螺稳定、速率陀螺稳定［1-2］、半捷联陀螺(导弹陀螺)稳定［3-4］以及地磁效应稳定［5-6］。目前上述几种稳定方式的滚转稳定平台国外都已经成功应用于火箭弹、迫击炮中，而国内在相关方面的研究起步较晚，有关的文献和研究不多。

由于速率陀螺本身精度限制，基于速率陀螺稳定的滚转稳定平台对角度和速度控制精度要求很高。尤其是在载体滚转速度急剧上升的时期，稳定平台采用传统PID控制器的控制精度难以令人满意。

本文在对速率陀螺式滚转稳定平台进行详细分析的基础上，推导建立了稳定控制系统的传递函数模型。在此基础上，设计了一种预测前馈复合控制器来提高稳定速度控制精度。最后采用DSP实现了预测前馈控制器并进行了验证实验。

1速率陀螺式滚转稳定平台原理

滚转稳定伺服平台的系统结构如图1所示，伺服编码器安装于转子的一端，用来测量伺服电机的转子位置和速度信号，作为伺服电机控制的反馈信号。惯性陀螺安装于电机转子的另一端，用来测量稳定平台的稳定角度和速度。而伺服控制系统根据惯性陀螺负载的反馈信号，控制伺服电机向载体滚转相反方向旋转，使惯性陀螺负载始终稳定在指定角度和速度范围内，实现稳定目的。

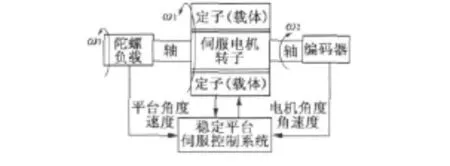
图1 滚转稳定平台的系统结构图

以大地为参照系，假设载体滚转角速度为ω1;伺服电机旋转角速度为ω2;稳定平台的稳定速度ω3。根据牛顿第二定律有:

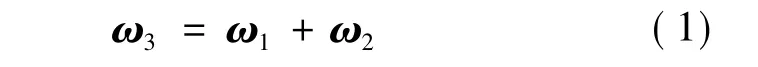
由于惯性陀螺角度和速度精度范围限制，为保证陀螺的输出不饱和，滚转稳定平台的伺服系统必须同时控制角度和速度。陀螺式滚转稳定平台选用永磁同步电动机作为伺服电机，其伺服电机控制原理如下:

在图2中，采用id=0的矢量控制，矢量变换的角度来自于伺服编码器的测量角度，而速度环和位置环以惯性陀螺测量装置的信号作为反馈信号。

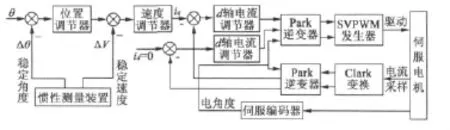
图2 滚转载体稳定平台伺服控制原理图

2伺服控制系统模型推导

永磁同步电动机以三相星型连接，假设:1)电机内磁路不饱和、电感不受电流变化的影响;2)忽略磁滞和涡流损耗;3)电机内磁场呈正弦分布在此假设条件下，则永磁同步电动机在d-q坐标系下的电压方程:

式中:Rs为绕组相电阻;Ld和Lq分别为d、q轴线圈的自感;p为微分算子;ud和uq分别为电压在d轴和q轴的分量;id和iq分别为电流在d轴和q轴的分量;ω为机械角速度;ψf为电机的永磁磁通;p为电机极对数。

采用id=0控制，将式(2)化简得到d-q坐标下电流的微分方程:

电机的电磁转矩方程:

不计摩擦的电机运动方程:

式中:J为电机轴上的转动总惯量;Te为输出电磁转矩。将式(3)～式(5)进行拉氏变换后整理得传递函数:

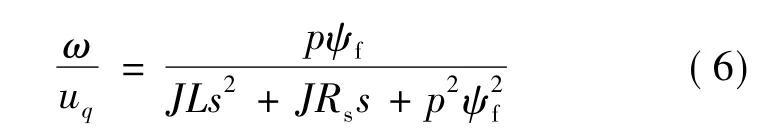
令ke=km=pmψf，永磁同步电动机采用电流反馈型脉宽调制逆变驱动，电流环采用PI控制器，得到永磁同步电动机电流环的模型框图如图3所示。

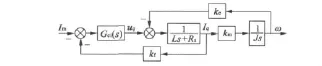
图3 滚转稳定平台伺服系统电流环控制模型图

图中，Gci为伺服系统电流环的控制器传递函数;kf为电流的反馈传递系数;ke为电机的电势系数;km为电机的力矩系数。

根据图3，整个电流环传递函数:

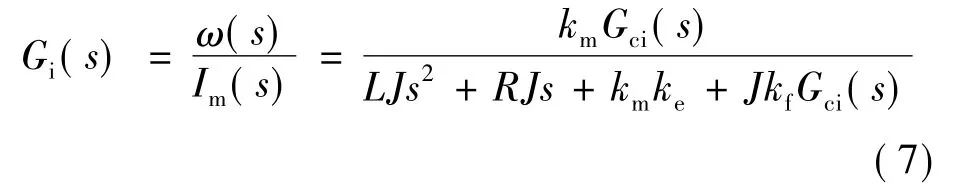
结合式(1)、图2、图3，整个滚转稳定伺服系统控制框图如图4所示。

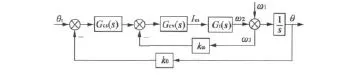
图4 滚转稳定平台伺服控制系统框图

图中，kw为速度系数;kθ为角度系数;θr为输入稳定角度，通常为零;Gcv(s)和Gcs(s)分别是速度控制器和位置控制器的传递函数，速度和位置控制通常采用PID控制。

从图4可知，对滚转稳定平台的伺服系统来说，载体滚转速度ω1为控制系统的扰动信号。当弹体静止ω1等于零时，稳定平台伺服系统就是通常意义上的位置伺服系统;当弹体滚转ω1不为零时，稳定伺服系统是一个受载体滚转速度干扰的控制系统，使用传统PID控制不能很好抑制速度干扰，需要寻求新的控制方法来抑制系统干扰。

3预测前馈复合控制设计

在滚转稳定平台中，由式(1)可知，载体旋转扰动速度ω1可以通过伺服编码器和惯性陀螺测量速度计算得到，根据前馈复合控制理论，得到滚转稳定平台前馈复合控制系统框图如图5所示。

图5 滚转稳定平台前馈复合控制系统框图

根据全补偿原则，滚转稳定平台扰动信号前馈通道传递函数:

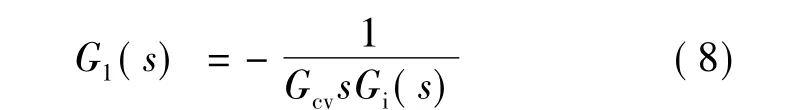
在实际系统中，式(8)控制器往往不能完全实现，通常采用静态前馈的形式代替。由于滚转稳定平台对系统动态性能要求高，这种静态前馈不能很好地适应系统动态性能的要求。这里考虑将模型预测控制跟前馈控制结合起来，用模型预测模块来代替前馈通道传递函数的计算，这样既能发挥前馈控制的优势，又便于工程实现。

已知当前时刻可测干扰为ω1(k)，由于采样频率较快，假设预测l时刻内干扰保持不变，即有:

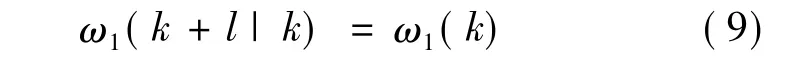
式中:ω1(k+l|k)表示由k时刻信息预测的k+l时刻速度干扰值。

当干扰输入为零，角度参考信号为零，输入阶跃前馈控制u，根据图5传递函数，由阶跃响应模型可以测得前馈控制作用u对输出的阶跃θ的阶跃响应系数，表示为 H={h1，h2，…，hn}，其中，N 为阶跃响应的截断时域长度。同理得到干扰ω1对输出θ阶跃响应系数，设 F={f1，f2，…，fn}。则可得干扰 ω1和前馈控制器输出u，图5对系统输出角度ω1的影响可用下式表示:

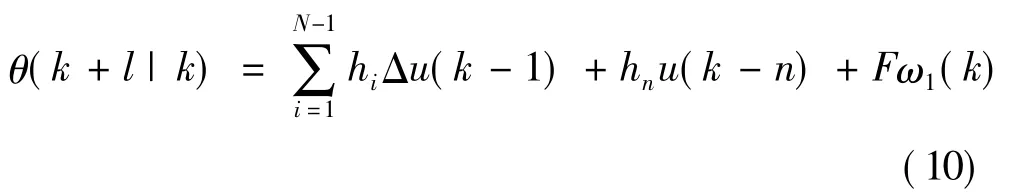
式中:Δ=-z-1表示差分算子，z-1为后移算子。预测控制的目的就是求取最优前馈控制作用u，使得式(10)达到最小值。将得到的最优控制作用u(k)作为前馈同道的输出与反馈控制器输出一起作用对象。在下一时刻，由测得的ω1(k+1)重新滚动计算最优控制作用，形成滑动优化预测控制。

由Garcia的动态矩阵控制器，综上模型预测前馈控制器最终表述如下［7］:

性能指标函数:

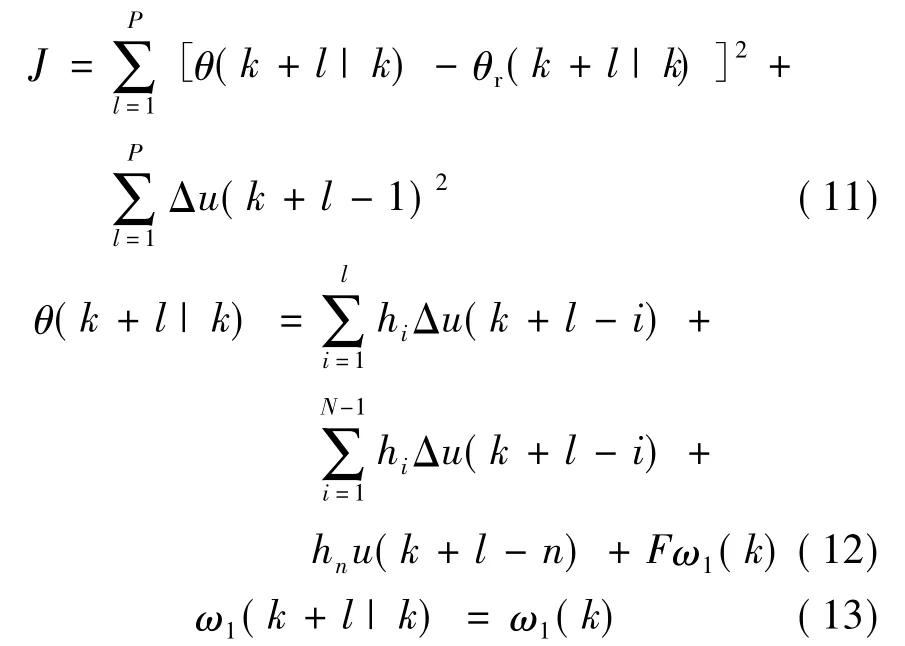
式中，θ(k+l|k)为当前k时刻的信息预测k+l时刻θ值;P为预测长度。经过对性能指标J求最小值，以及上述公式最优控制问题的滚动求解，得到前馈控制的控制输出，对系统进行控制。

4实验

在实验室建立滚转稳定伺服试验平台，如图6所示。

模拟电机带动稳定伺服电机定子一起旋转，用来模拟弹体滚转角度和速度，模拟电机控制系统采用变频器控制。而伺服电机轴的一端接有伺服编码器，用来测量伺服电机转子的角度，用于矢量控制变换角度;而惯性陀螺安装于电机轴的另一端，用来测量滚转稳定平台输出的角度和速度。

图6 滚转稳定平台试验系统示意图

伺服电机控制系统是以 DSP芯片TMS320F2812为核心，构建了前述的基于空间矢量脉宽调制算法的位置、速度、电流三闭环控制系统，通过DSP编程实现上述前馈预测控制算法和PID控制器。

上位机通过模拟电机控制系统下载模拟曲线，通过变频器控制模拟电机按照指定曲线运行，同时上位机还需要与DSP伺服控制系统通讯，实时接收、记录以及显示稳定平台一些参数。

模拟电机主要电机参数如下:额定功率为3．7 kW，额定转矩18 N·m，额定转速为2 000 r/min，额定电流为8 A，该电机采用ABB公司的ACS800变频器控制。伺服编码器和模拟编码器采用12位绝对式光电编码器。

伺服永磁同步电动机参数如下:额定电压U=27 V，额定电流I=3 A，定子相绕组 Rs=0．42 Ω，d、q轴相绕组电感Ld=Lq=0．45 mH，永磁磁通 φ=0．004 343 Wb，极对数 p=2。总转动惯量 J=0．000 635 kg·m2;负载陀螺的最大速度输出为300°/s。

稳定平台伺服系统分别采用纯PID反馈控制和预测前馈PID反馈复合控制进行试验，上位机以1 ms周期采集数据，最后用MATLAB将采集的数据进行绘图如图7～图12所示。

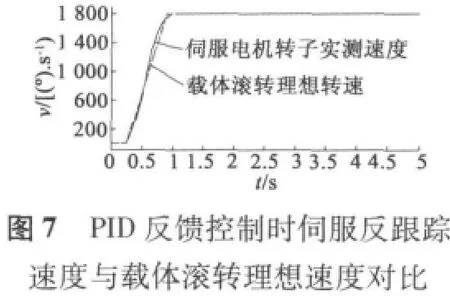
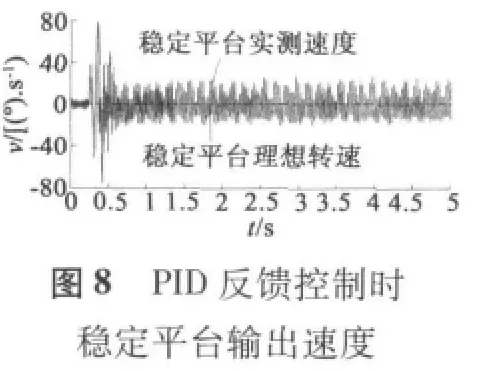
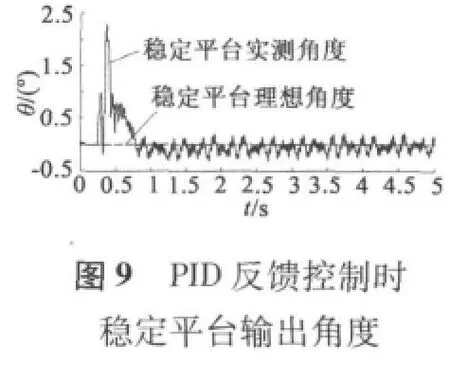
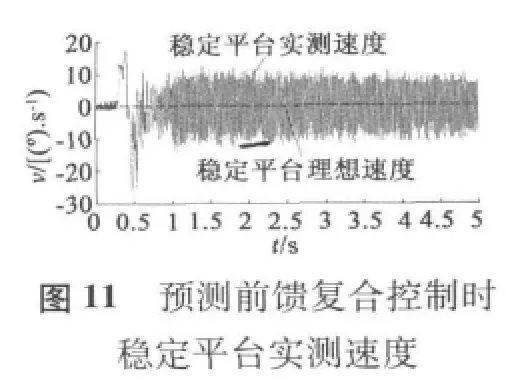
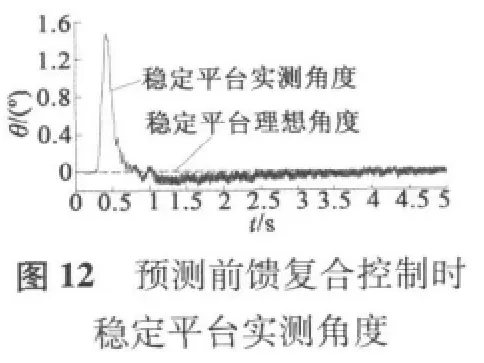
图中，载体滚转速度试验曲线由两部分组成，第一部分速度上升部分，大约0．7 s内速度从零提升到1 800 r/min，最大加速度大于 7 500°/s2，用来模拟弹体在弹膛点火弹体旋转速度急剧增加的过程，这可以检测稳定平台伺服系统的动态性能。第二部分速度稳定运行部分，时间为4 s，载体滚转速度稳定在1 800 r/min，用来模拟弹体在控制飞行过程，可以检测稳定平台的稳态性能。

从图7至图12看出，无论是PID反馈控制和预测前馈控制，在动态和稳定情况下，稳定平台的稳定速度不超过80°/s，稳定平台的稳定角度在2．5°以内，可看出惯性陀螺式稳定平台精度较高。

载体滚转速度动态上升阶段，图8显示PID反馈控制下平台的稳定速度最大为±80°/s内，图9显示对应的稳定角度最大为2．3°，图11显示预测前馈复合控制下平台的稳定速度±25°/s，图12显示相应的稳定角度最大为1．5°;当载体滚转速度稳定运行时，图8显示PID反馈控制下平台的稳定速度最大为±20°/s内，图9显示对应的稳定角度为±0．3°，图11显示预测前馈复合控制下平台的稳定速度±10°/s，图12显示相应的稳定角度最大为±0．1°。从上看出，预测前馈复合控制的控制精度比单纯PID控制精度更高。