永磁同步直线电动机的自适应模糊滑模控制

吴 奎，高 健，汪志亮，陈 新

(广东工业大学，广东广州510006)

0引 言

永磁同步直线电动机中具有机械结构简单，无反冲、低摩擦阻力，可执行长距离高速高精度定位等优势，已经广泛应用于工业机器人、数控机床等高性能驱动设备中，随着微电子、控制技术、电力电子技术和精密加工技术的进一步发展，直线电动机的应用领域将不断地扩大［1］。然而，永磁直线同步电动机存在的齿槽效应、永磁体磁链谐波等产生的推力纹波、系统参数(动子质量、粘滞摩擦系数等)变化、外部负载扰动、端部效应等因素将使伺服性能变坏［2］。为了保证系统的伺服性能，许多研究人员致力于将滑模变结构控制算法用于永磁同步直线电动机的控制上。

滑模变结构控制具有快速性、稳定性和实现简单的特点。文献［3］利用遗传算法优化了模糊变量的隶属度函数曲线，使系统的响应更快速，并能降低滑模变结构算法的抖振使系统更稳定。

文献［4］提出了基于扰动补偿的滑模控制算法，实时地跟踪负载推力的变化，提高了系统对外部扰动的鲁棒性。文献［5］将自适应模糊滑模控制用于旋转电机伺服系统中，用模糊控制器来模拟反馈线性化控制律，取得了较好的控制效果。文献［6］运用滑模变结构控制对永磁同步直线电动机的直接推力进行控制，验证了采用滑模变结构控制器对动子电阻变化而引起的动子磁链观测角度误差有较强的鲁棒性。文献［7］在运用滑模变结构算法对永磁同步直线电动机进行控制的同时，还通过线性推力观测器并联一个神经网络观测器相加实现对系统的扰动补偿。此方法增强了伺服系统对参数摄动和外在扰动的稳定性。文献［8］利用自适应律对系统不确定性扰动因数的极限进行估算，增强了滑模变结构位置控制器的信号跟随性能。文献［9］采用自适应模糊滑模控制策略来实现欠驱动平面机械手的位置控制，较好地实现了机械手的位置控制，验证了滑模变结构算法具有很强的鲁棒性和快速性。文献［10］用饱和函数msat(t)代替理想滑动模态中的符号函数sgn(t)，并运用线性化反馈方法设计滑模控制器，从而实现一个新型的非线性滑模变结构鲁棒控制。文献［11］将模糊自适应滑模控制用于速度频繁大幅度变化的场合，并与使用了粒子群优化算法的PI控制器进行比较，验证了模糊自适应滑模具有很强的鲁棒性和准确性。

本文结合当前先进的智能控制算法，提出一种新颖的自适应模糊滑模变结构控制算法，即采用积分滑模面切换设计函数，并采用自适律和模糊逼近理论来逼近滑模控制器的输出，最后还应用自适应的切换控制器对滑模控制器的输出进行补偿。算法经仿真验证，实现了对永磁同步直线电动机在高加速度运动条件下的高精度控制。

1永磁同步直线伺服电机的数学模型和推力表达

永磁同步直线电动机是一种性能很好的直线伺服电动机，它具有推力强、损耗低、响应快等优点。

对永磁同步直线电动机进行数学建模，为了进行原理仿真，需要作如下假设［1］:

(1)忽略铁心饱和，忽略涡流和磁滞损耗;

(2)永磁体的电导率为零;

(3)动子绕组阻尼为零;

(4)相绕组中感应电动势波形为正弦。

有了以上假设，当我们仅考虑基波分量，在dq坐标轴下，永磁同步直线电动机的数学模型可通过电压方程和推力方程表达如下［1］:

d轴电压平衡方程:

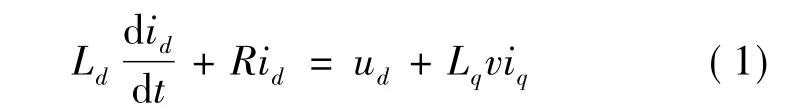
q轴电压平衡方程:

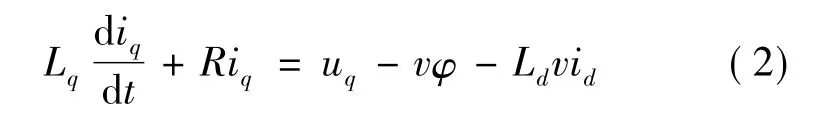
电磁推力Fm:

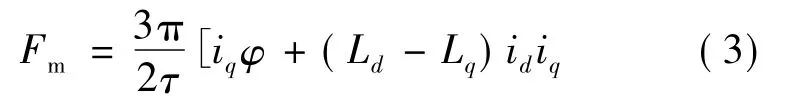
机械运动方程:

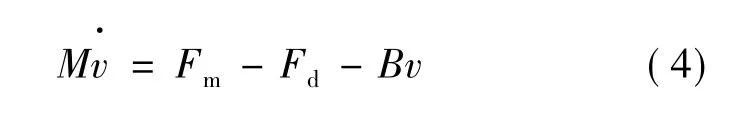
下面对永磁同步直线电动机进行矢量控制。矢量控制通过矢量变换消除励磁控制回路和推力回路之间的耦合。为了获得矢量控制的效果，必须令id=0。此时，永磁同步直线电动机的推力方程［1］:

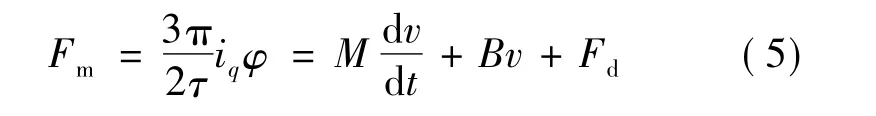
式中:id为动子d轴电流;iq为动子q轴电流;ud为动子d轴电压;uq为动子q轴电压;Ld为动子d轴电感;Lq为动子q轴电感;R为动子电阻;M为动子质量:B为摩擦系数;v为电机移动速度;τ为磁极距;φ为电动机永磁体磁链;Fd为负载阻力。

永磁同步直线电动机的矢量控制系统图如图1所示。

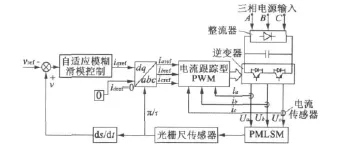
图1 永磁同步直线电动机矢量控制图

2自适应模糊滑模控制器的设计分析

滑模变结构控制是典型的鲁棒控制。由于滑动模态可以进行设计且与对象参数及扰动无关，因此具有设计简单且鲁棒性强的优点。模糊控制可以对误差进行映射到特定的、较小的值域，有利于削弱滑模控制的抖动程度。自适应控制能够自动对外界总不确定性的上界进行估计，保证了滑模控制系统能满足李雅普诺夫稳定性条件，从而保证系统能到达一致稳定。自适应模糊滑模变结构控制方法是一种吸收了上述三种先进算法的新型控制算法，具有更强的鲁棒性。

2．1基于积分滑模面的滑模控制

考虑如下单输入单输出的非线性系统:

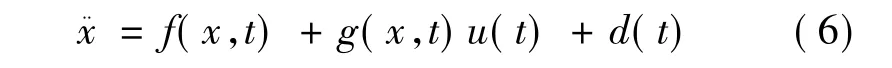
式中:f和g均为未知非线性函数，g＞0，u为控制输入函数，x为系统输出信号函数，d(t)为外加干扰。

跟踪误差:

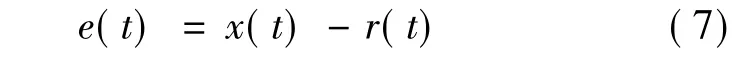
式中:r为实际输出的检测信号函数。定义积分滑模面:

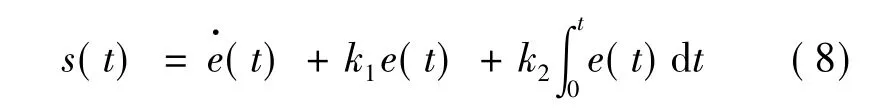
式中:k1和k2为非零正常数。

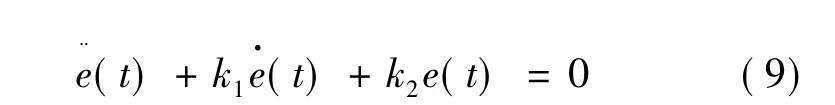
通过确定k1和k2，跟踪误差e(t)将趋近于零。

假设f、g及d(t)为已知，根据式(6)～式(9)，可求得理想的控制器:

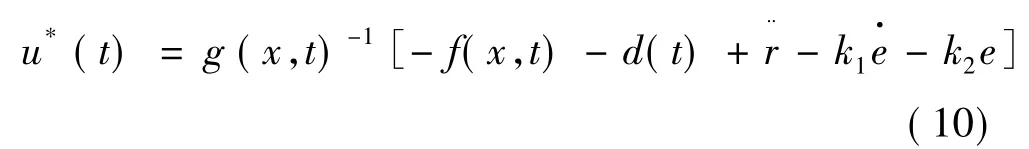
2．2自适应模糊控制器的设计思路

为了减少模糊系统的输入变量的数量，提高模糊系统的运输速度，本文采用滑模面函数s(t)作为模糊控制器的输入，实现了只有一个输入变量的模糊系统。

当f、g和d(t)均为未知时，u*(t)难以用线性方程实现，可采用模糊系统来逼近u*(t)。取ai为可调参数，使用重心法进行反模糊化处理，可得到模糊控制器的输出函数:

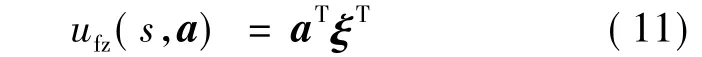
式中:a=［a1a2… am］T，ξ =［ξ1ξ2… ξm］。ξ定义:

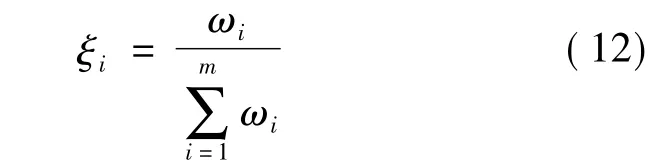
式中:ωi为第i条规则的权值。

根据模糊逼近理论，存在一个最优模糊系统ufz(s，a*)来逼近 u*(t)。

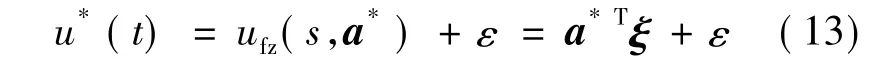
ε为实际逼近误差，满足|ε|＜E的条件。

使用模糊控制输入函数ufz逼近u*(t)时，则:

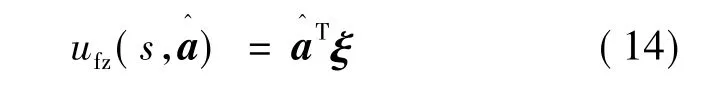
切换控制函数uvs用来补偿u*与ufz之间的误差，则总的自适应模糊滑模控制函数:

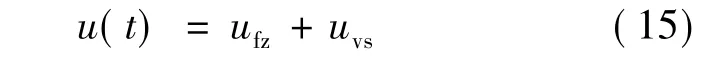
由式(13)定义:

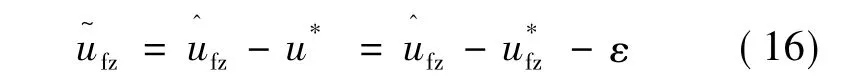
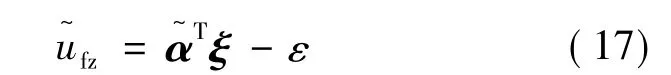
由式(8)得:

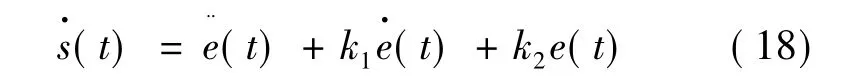
则式(10)变为:

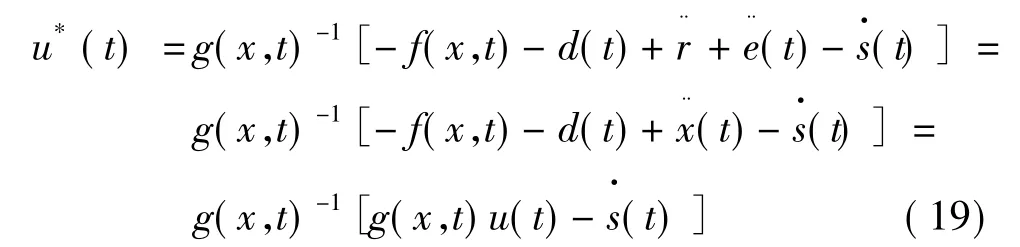
由式(10)和式(14)得:

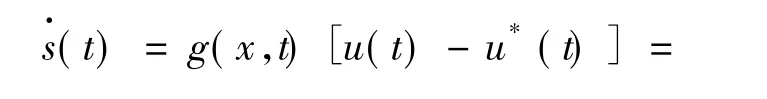
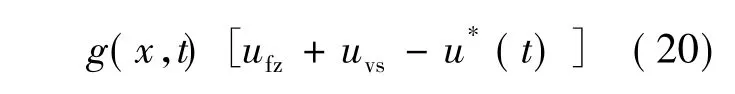
定义Lyapunov函数:

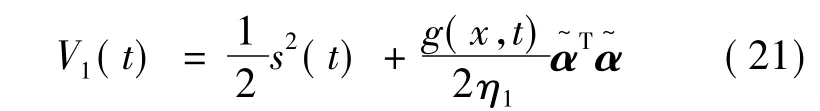
式中:η1为正的实数。则:

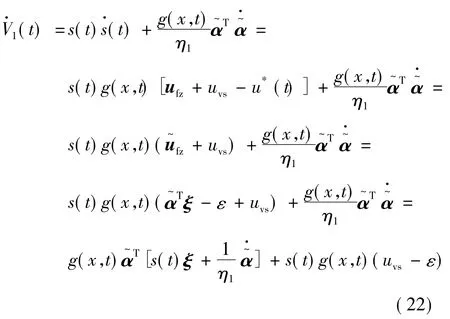
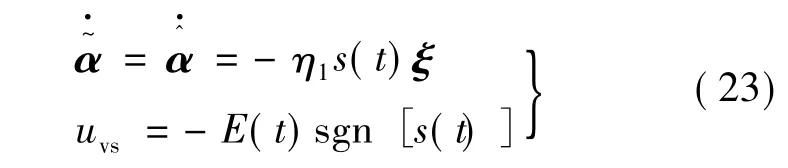
则式(22)变为:

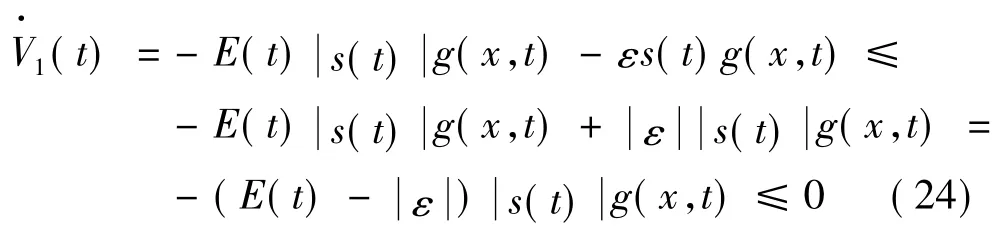
在滑模切换控制过程中，切换增益E(t)值会变化较大。以往的控制过程中往往是通过经验来确定的。如果E(t)值偏大，则系统会产生剧烈的抖振;如果E(t)值过小，则控制系统会变得不稳定。

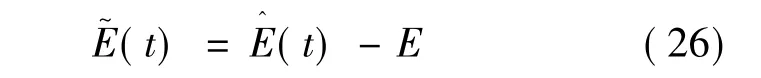
定义Lyapunov函数为:

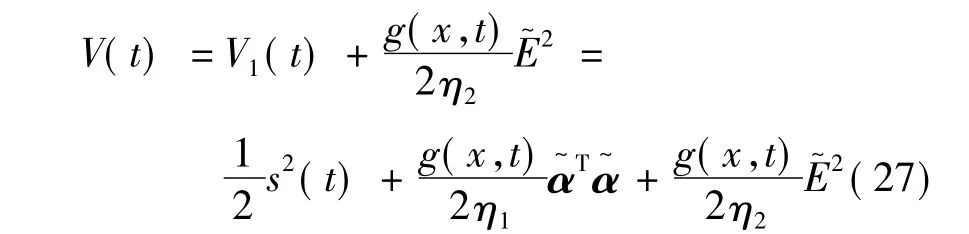
式中:η1和η2为正的常数。则:

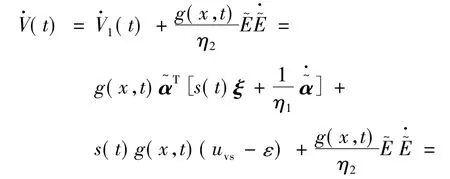
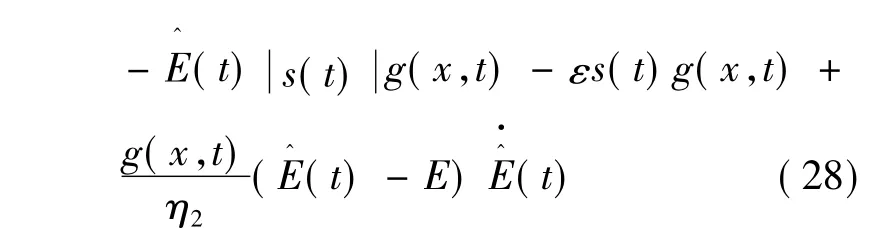
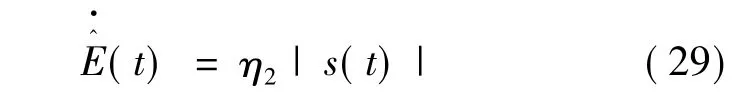
则

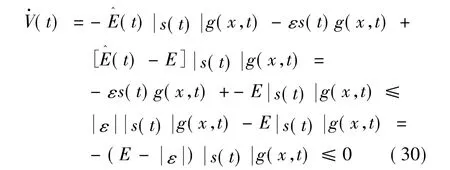
2．3自适应模糊滑模控制器在Simulink中的实现

从上一节的分析可以知道，自适应模糊控制器首先采用模糊规则对滑模面函数s(t)进行模糊化处理，然后在使用反重心法进行模糊输入时采用了满足李雅普诺夫稳定的自适应律，最终实现了自适应模糊控制。另一方面，在对自适应模糊输出进行补偿时，采用了线性的自适应滑模切换控制，最终构成了能够对时变非线性系统进行控制的自适应模糊滑模控制器，如图2所示。

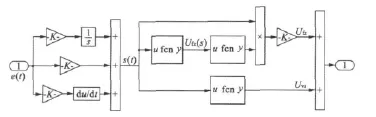
图2 自适应模糊滑模控制器

3仿真实验与分析

在MATLAB 7．1版本的Simulink模块中对整个直线电动机运动控制系统进行建模仿真，系统控制图如图3所示。

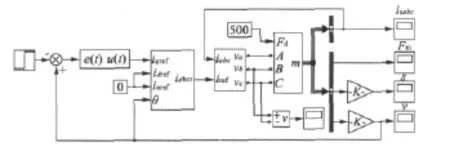
图3 自适应模糊滑模直线电机控制系统

永磁同步直线电动机的仿真参数选取如下:电感 Ld=18．74 mH、Lq=18．74 mH;电阻 R=1．2 Ω ;质量M=25 kg;摩擦系数B=0．2 N·s/m;磁极距τ=36 mm;磁链值ψ=0．286 Wb;负载阻力初始值Fd=500 N，0．1 s时变为Fd=200 N。目标输入为阶跃信号vref=1 m/s。

自适应模糊滑模直线电动机控制系统仿真结果如图4～图7所示。

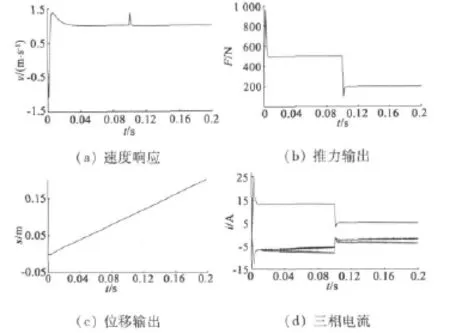
图4 直线电动机自适应模糊滑模仿真结果

为了验证本文提出的自适应模糊滑模控制算法的优越性，下面进行PID-PMLSM的对比仿真，选取 Kp=60，Ki=250，Kd=0．5，结果如图 5 所示。

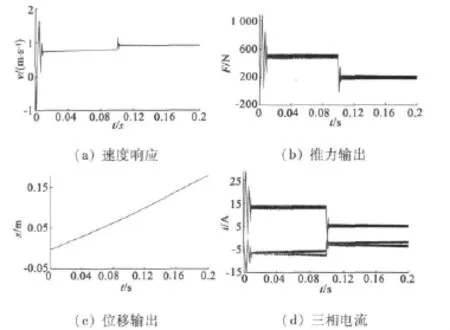
图5 PID永磁同步直线电动机控制仿真结果

比较图4、图5可知，永磁同步直线电动机伺服系统在采用本文提出的自适应模糊滑模控制算法控制时，对负载的变动更具有强的鲁棒性;而且比传统的PID控制的位移输出精度高;推力输出的波动小。在电机起动时，仿真系统加上的变化负载(500 N～200 N)，模拟了实际运行中的系统从高加速变为平稳匀速运动的情况，反映了自适应模糊滑模控制算法具有更好的高加减速运行特性。

4结 论

(1)由速度输出对比图和推力输出图可知，本文提出的自适应模糊滑模控制算法比传统的PID算法根据快速稳定性，在大推力输出和推力变化时更是表现出较强的鲁棒性和抗干扰能力。

(2)由位移变化图可以得出，采用自适应模糊滑模控制算法的直线电动机控制系统的位移输出精度更高，更能满足高加减速直线电动机运动平台的精密定位要求。

(3)由电流电压输出图可以知道，采用自适应模糊滑模控制算法的直线电动机控制系统的电流更平稳，从而抑制了系统的磁链变化，更能克服直线电动机端部效应对推力稳定性的影响。

经过对仿真结果的分析对比可知，本文提出的运用积分滑模面的自适应模糊滑模控制算法具有正确性和可使用性。在用于永磁同步直线电动机控制时，提高了永磁同步直线电动机控制系统的位移输出精度和抗干扰能力。

［1］ 郭庆鼎，王成元，周美文，等．直线交流伺服系统的精密控制技术［M］．北京:机械工业出版社，2000．

［2］ 叶云岳．直线电机技术手册［M］．北京:机械工业出版社，2003．

［3］ 董科．永磁直线同步电机自适应变结构位置控制器的研究［J］．沈阳大学学报，2010，22(3):4-7．

［4］ 高文达，方一鸣．自适应模糊滑模控制在伺服电动机系统中的应用［J］．微特电机，2009(11):32-36．

［5］ 黄辉先，阮挺．基于遗传算法的模糊滑模控制在永磁直线电机位置控制中的应用［J］．湘潭大学自然科学学报，2010，32(4):94-98．

［6］ 仇翔，孙航．基于扰动补偿的永磁同步直线电动机滑模控制［J］．电气传动自动化，2008，30(1):14-17．

［7］ 杨俊友，崔皆凡，何国锋．基于空间矢量调制和滑模变结构的永磁直线电机直接推力控制［J］．电工技术学报，2007，22(6):24-29．

［8］ 付子义，李华群，王振锋．基于神经网络推力观测器的永磁直线电机滑模控制［J］．电气传动，2009，39(11):48-51．

［9］ 王洪斌，焦守江，佘君．欠驱动平面机械手自适应模糊滑模控制［J］．系统仿真学报，2006，18(7):1893-1896，1901．

［10］ Zhang Xi，Pan Junmin．Nonlinear Robust Sliding Mode Control for PM Linear Synchronous Motors［C］//IPEMC．Shanghai，China，2006．

［11］ Ghaebi Panah P，Ataei M，Shafiei A．An Adaptive Fuzzy Sliding Mode Control of a Permanent Magnet Linear Synchronous Motor for an inimical Command Velocity Profile［C］//ICSET．isfahan，Iran，2004．