基于CVaR风险控制下的多阶段投资组合优化模型

贺月月，高岳林，李 维

（1.北方民族大学信息与系统科学研究所，银川 750021；2.陕西凌云电器集团公司，陕西宝鸡 721006）

0 引言

投资组合优化是现代金融理论研究的起源和动力之一，其思想简言之，就是把财富分配到不同的资产中，以达到分散风险、确保收益的目的。1952年，Markowitz提出的均值-方差模型［1］，是现代投资理论的基础。该理论以静态的观点研究和论述投资组合的理论和方法。但实际的投资组合问题具有动态特征，由于在不同时期，资产的收益率不同，以及投资者对风险和收益的偏好会发生改变，投资者将考虑以最大化终端财富建立多阶段投资组合策略，周期性地平衡资产投资比例。MC Chan等［2］结合各种特定情况的随机性分析，用某一种特定情况描述整个多阶段投资周期的某一单一路径，建立了多阶段投资组合模型。

1993年，国际清算银行提出的一种针对市场风险的资本金要求的风险度量方法—VaR，尽管它是目前一种应用比较广泛的风险度量，但是VaR作为投资组合x的函数，存在一些缺点，尤其体现在资产分布存在尖峰厚尾性，同时VaR还不满足次可加性，而次可加性是一致性风险的重要性质。基于VaR的这些缺陷，一种新的风险度量——条件风险价值(conditional value at risk，CVaR)被提出来，CVaR也被成为尾部VaR、额外损失的均值或平均损失[3][4]。因为CVaR具有次可加性和凸性，在数学上容易处理，从而CVaR的研究成为国内外的热点。

本文拟将条件风险价值CVaR约束引入到文献[2]的模型中，运用带有罚函数处理机制的差分进化算法[5]求解新的多阶段投资组合模型，并对新模型进行实证分析，验证其有效性。

1 多阶段投资组合优化模型

假设资产市场上存在n种风险资产，1种无风险资产(用1号表示现金)，投资者在初始0时刻进入市场，开始为期T个阶段(t=1,2,…,T)的投资活动。模型结合各种特定情况的随机性分析，用某一种特定情况描述整个多阶段投资周期的某一单一路径[6]，某一特定情况由市场指数的变化定义，为了简洁设置两种特定情况为市场指数下降和市场指数上升，如图1所示。投资组合模型的描述如下[7]：

（1）参数

表示路径s下第t阶段资产i的收益率；

②πs表示从整个周期开始到周期结束路径s发生的概

③W0表示投资开始时的财富总量；

④表示路径s下第t阶段结束时的所有财富总量；

⑤表示路径s下第t阶段开始时重新平衡资产分配之前资产i的财富总量；

⑥T是阶段总数；

（2）决策变量

①表示路径s下第t阶段开始时重新平衡资产分配之后资产i的财富总量；

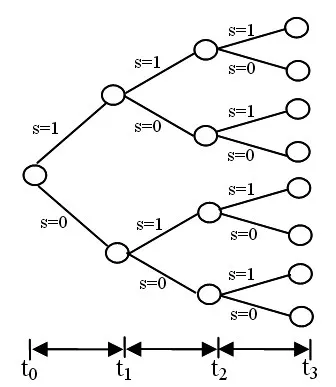
图1 拥有两种特定情况和三个阶段的情景树

②表示路径s下第t阶段开始时为了重新平衡资产而需买入资产i的总量；

③表示路径s下第t阶段开始时为了重新平衡资产而需卖出资产i的总量；

（3）多阶段投资组合优化模型

其中，i=1,2,…,n+1；s=1,2,…,S;t=1,2,…,T。MeasureTs是路径s下第T阶段所用效用函数。γ是投资者根据自己对投资风险的容忍程度设定的参数：γ值越小，表示投资者对投资风险敏感，γ=1是效用函数值是阶段结束时不考虑投资风险的财富量。

在模型(1)中，第一、二个约束条件表示初始化时的总财富量；第三个约束条件表示路径s下每个阶段t开始时的总财富量；第四个约束条件表示路径s下资产i平衡前财富量与前一阶段积聚的财富量的关系；第五、六个约束条件表示现金和其它种类资产在特定情况s下平衡后的财富量；第七个约束条件表示任何阶段平衡前每一种资产在所有路径下的价值相等。

2 基于CVaR风险控制下的多阶段投资组合优化模型

2.1 条件风险价值(CVaR)[8]

是投资组合x的益损函数，向量y表示影

响益损的不确定性，如市场价格或收益率，对任意x，由y

是服从某一分布的随机变量。为方便

起见，假设y的密度函数为

不超过某一阈

值的概率为

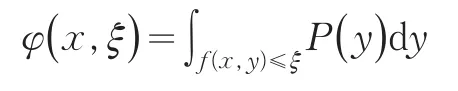
固定x时，作为ξ的函数φ(x,ξ)是同x相关的益损的累积分布函数，在给定置信水平α下的VaR与CVaR值分别为

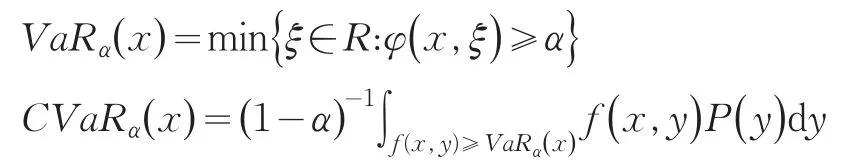
VaRα(x)是包含值ξ的非空区间的左端点，因此，则的概率为1-α。因此CVaRα(x)是益损f(x,y)大于等于VaRα(x)的条件期望。

假设资产的收益率服从正态分布的情况，由CVaR的定义，得益损f(x,y)在置信水平下的CVaR为

其中，R(x)为投资组合的期望收益，σ(x)为R(x)的标准差，ϕ为标准正态分布的分布函数，ϕ-1(α)为标准正态分布的α-下侧分位数，ψ()⋅为标准正态分布的概率密度函数。

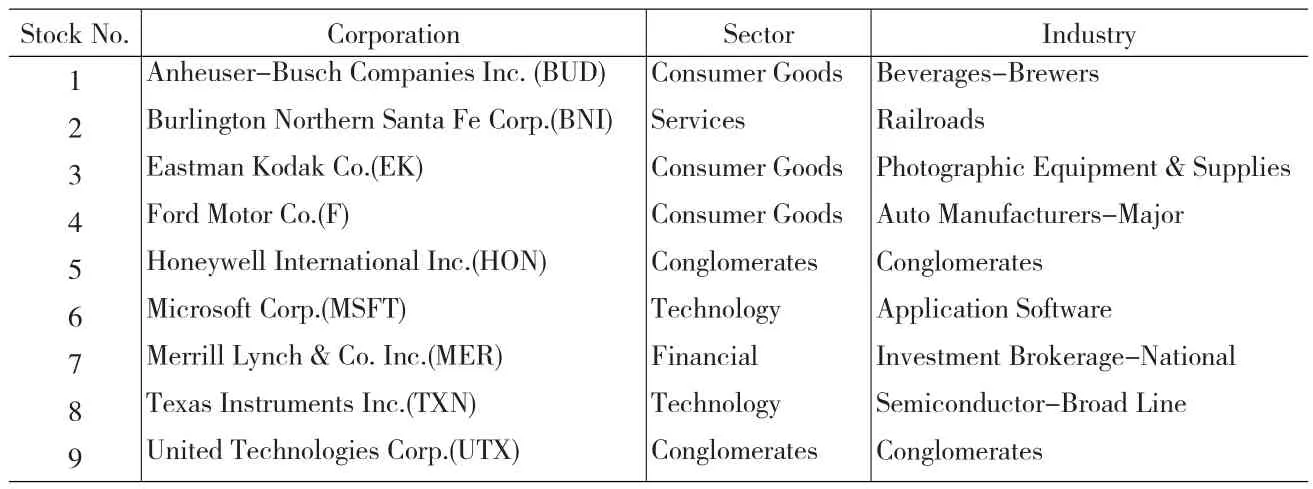
表1 选取的美国标准普尔指数100的9只成分股

2.2 模型的建立

考虑到投资者在追求高收益的同时，希望风险尽可能小，或者将风险控制在一定水平下，期望收益尽可能大。从而，在不允许卖空的情况下，引入条件风险价值CVaR约束，则新模型如下

表2 三个阶段各条路径发生的概率

表3 特定路径下各阶段的最优投资策略

表4 特定路径下各阶段的最优投资策略

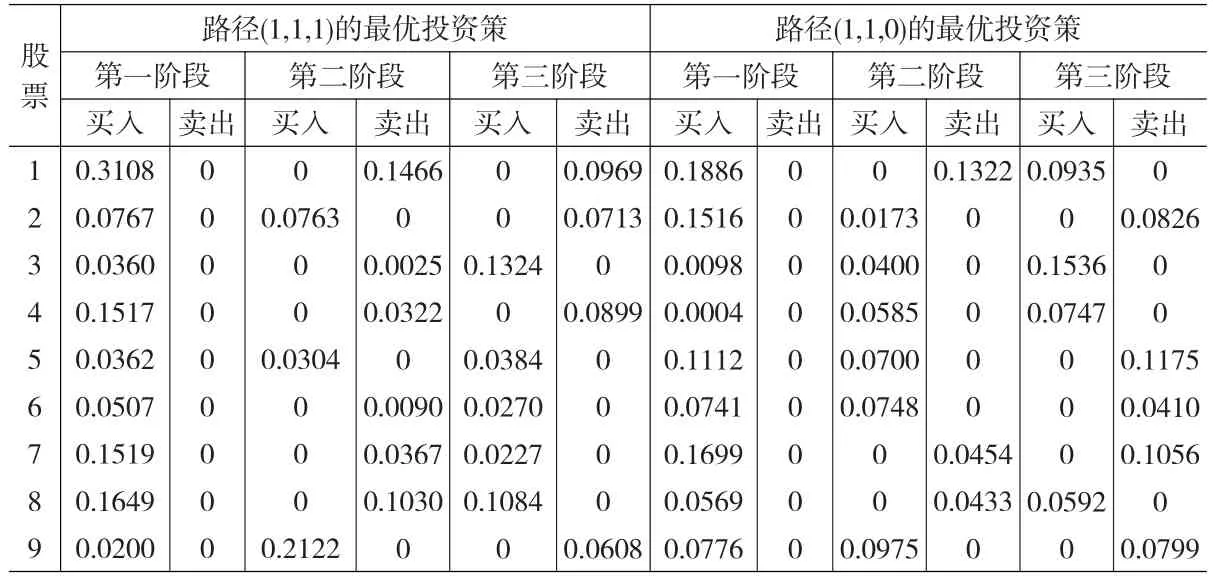
表5 特定路径下各阶段的最优投资策略

表6 风险阈值ω=0.5时，不同置信水平下的条件风险价值

其中，i=1,2,…,n+1；s=1,2,…,S；t=1,2,…,T。Rst为路径s下第t阶段资产组合的期望收益，σst为Rst的标准差，ϕ为标准正态分布的分布函数，ϕ-1(α)为标准正态分布的α-下侧分位数，ψ(⋅)为标准正态分布的概率密度函数.第一个约束条件表示在给定的置信水平α下，将路径s中每个阶段的条件风险价值CVaR都控制在阈值ω范围内。

利用罚函数方法[9]将模型(2)转化成如下形式

其中，i=1,2,…,n+1；s=1,2,…,S；t=1,2,…,T;δ为惩罚因子，一般选取105～108。

3 实证分析

表7 不同置信水平与风险阈值下的期望收益

本文借鉴文献[7]的数据，如表1和表2所示。路径用0-1二进制代码表示，1表示市场指数上升，0表示市场指数下降(如010表示第1、3阶段市场指数下降，第2阶段市场指数上升)。

现将9只股票和银行存款作为一项投资，投资阶段数T=3，假设模型(3)中的惩罚因子δ=106。在MATLAB中运用差分进化算法来实现，参数分别设置为：种群规模NP=100,最大迭代次数Tmax=500，缩放因子F=0.3，变异概率由CRmax=0.9到CRmin=0.5逐步递减。置信水平α分别取90%、95%、99%，程序均独立运行30次。

(1)当α=90%时，期望收益为1.0042，得到最优投资策略如表3所示。

(2)当α=95%时，期望收益为1.0044，得到最优投资策略如表4所示。

(3)当α=99%时，期望收益为1.0045，得到最优投资策略如表5所示。

表3～5分别给出了置信水平α=90%、α=95%、α=99%下，资产组合路径(1,1,1)和路径(1,1,0)各阶段的最优投资策略。同样的，可以得到其他六条路径各阶段对应的最优投资策略。

由表6可知，在给定投资组合的风险阈值ω时，随着置信水平α的不断增大，CVaR值也不断增大，说明投资者厌恶风险的程度逐步增强，从而可根据自己的风险厌恶程度选择和制定投资方案。

在相同置信水平α下，将风险阈值ω由0.3逐步增加到0.9，如表7所示，期望收益不断增大；同一风险阈值ω下，随着置信水平α由90%逐步增加到99%，期望收益也不断提高。结合表6的结论可知，当置信水平越大时，条件风险价值越大，期望收益也越高，即高风险高收益。这也符合理论研究结果。

4 结束语

本文在不允许卖空的情况下，通过对资产组合的每一个阶段施加CVaR约束，即利用条件信息不断地对风险进行重新评估,从而对投资决策连续地施加影响，使投资者在投资过程中尽可能避免遭受非正常损失，并运用差分进化算法，分阶段地逐步调整投资比例，实现对资产组合收益的优化。该思想更符合实际投资情况，使投资者能选择适合自己风险偏好的投资组合策略。

[1]Markowitz H.Portfolio Selection[J].The Journal of Finance，1952，（7）.

[2]MC Chan，CC Wong，BK-S Cheung，Etal.Genetic Algorithms in Multi-Stage Portfolio Optimization System[A].Computing in Economics and Finance[C].Society for Computational Economics，2002．

[3]Chernozhukov Victor，Umantsev Len.Conditional Value-at-Risk，As⁃pects of Modeling and Estimation[C].Working Paper,Department of Eco⁃nomics，2000.

[4]Rockafellar R T，Stanislav Uryasev.Optimization of Conditional Val⁃ue-at-risk[J].Journal of Risk，2000，(2).

[5]刘波，王凌，金以慧.差分进化算法研究进展[J].控制与决策，2007，22(7).

[6]Berend Roorda．An Algorithm for Sequential Tail Value at Risk for⁃Path-independent Payoffs in a Binomial Tree[J].Ann Oper Res，2010，181（1）.

[7]须文波，江家宝，孙俊.基于QPSO算法的多阶段投资组合优化[J].计算机应用，2006，(7).

[8]高岳林，苗世清.基于VaR和CVaR风险控制下的M-V投资组合优化模型[J].统计与决策,2010，(5).

[9]高岳林，陈东志，鲍卫军.基于CVaR约束的单位风险收益最大投资组合模型及实证[J].统计与决策，2009，(13).