基于单摆的自动平板控制系统

王建行，李莉莉，刘娟意

(浙江海洋学院机电工程学院，浙江舟山 316004)

单摆是一种经典物理模型,它是一个形状、大小都可以看成质点的小球系在不计伸长和质量的摆线上的理想状态，各种单摆系统又是常见工程系统，基于单摆的应用和研究已经有很多，特别是在机械振动、汽车工程等领域具有重要的应用价值[1-3]。系统的控制离不开自动控制系统，自动控制系统是在无人直接参与下可使生产过程或其他过程按期望规律或预定程序进行的控制系统。自动控制系统是实现自动化的主要手段。本文设计一个基于单摆模型的自动控制系统：在单摆上安装一个可旋转的平板，基于单摆的运动，设计一自动控制系统，自动采集单摆的运动信息，分析处理后，进而控制平板的摆动，使置于平板上的物件在单摆自由摆动的情况下保持稳定，该单摆控制系统可有效应用到汽车抗震减震的研究中。

1 系统的实现目标和方案

图1是系统的机械结构图，摆杆的一端通过转轴固定在一支架上，另一端固定安装1台电机，平板固定在电机转轴上；当摆杆摆动时，驱动电机可以控制平板转动。该平板控制系统的具体控制目标是能够实现摆杆绕着转轴大角度旋转时(小于等于60°)，单摆上固定的可旋转控制平台能够保持稳定，平台上面的硬币(测试时最多8个)尽量不滑落。

如图2所示，本系统是由控制器模块、电机模块、角度检测模块、显示模块、电源模块等组成。

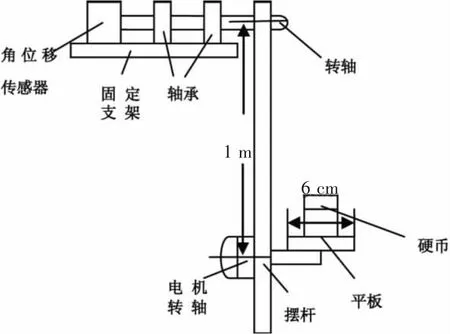
图1 系统机械结构图Fig.1 System mechanic structure

2 理论分析

在本设计中，系统的振动稳定性通过硬币置于平板，随着平板的摆动而不滑落来检验的，以摆动的角度、硬币的数量以及不掉落的概率等来衡量振动的稳定性。要提高稳定性，主要的理论分析包括：对平板和硬币、硬币与硬币间的摩擦系数进行研究、对平板上的硬币进行受力分析，对单摆大角度运动进行建模，考虑运动周期等因素，最后推导出单板摆动过程中，单摆摆动角度与平板和水平面的角度的关系，以保证硬币不滑落。下面就进行这方面的讨论。

2.1 系统的几何模型

图3是该系统受力分析时的参照几何图，其中θ为单摆摆杆与垂直线的夹角，α为平板与水平线的夹角。系统工作时，角度传感器测定摆杆与垂直方向的夹角θ，平板控制系统根据采集的角度数据θ进行算法分析，通过控制电机转动来调整平板的摆放角度α，从而使摆杆在进行大角度运动的情况下，进行自行调整而使硬币不滑落。

2.2 平板与硬币的摩擦问题

单摆的大角度运动属于自然不稳定系统，这种系统控制有两个必须研究的重要阶段：第一个阶段是起摆瞬间的控制问题；第二个阶段是中间平衡点的控制问题，涉及到力学模型和控制等学科。根据设计的需要，进行的指标的确定，单摆静止时，1个硬币放置于平板，α大于30°时一定要滑落(保证摩擦系数不要太大)，起摆的摆角在30°～60°时，通过平板的摆动使硬币尽量不滑动即保持稳定。为获得滑动系数等相关指标进行了实际的测试，单摆固定静止时，改变平板角度α，测试硬币起滑瞬间的α，经多次测试，包括顺时针和逆时针都有，取平均后数据见表1。

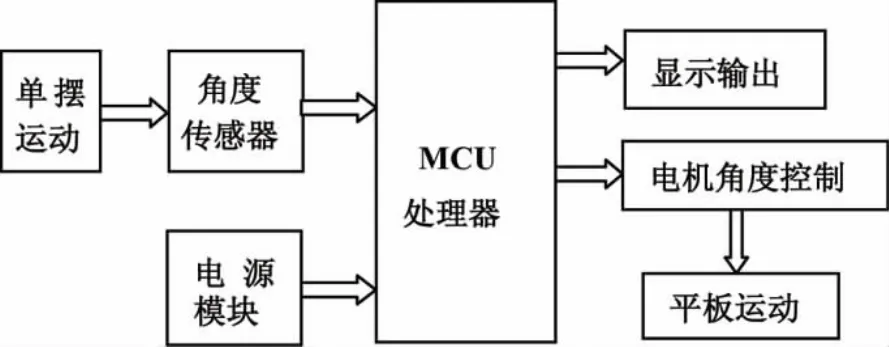
图2 系统功能框图Fig.2 System functional block diagram

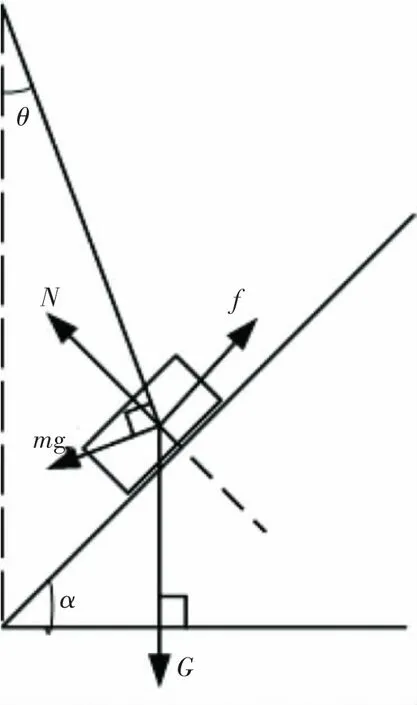
图3 几何图Fig.3 Mechanical analysis diagram

表1 起滑瞬间角度Tab.1 α at the moment of the coins starting to slide

表1中α与平板和硬币、硬币与硬币间的最大静摩擦力有直接关系。在低速情况下，根据摩擦力简化模型[4-5]，有

其中 Tf为干扰力矩，Tc为库伦力矩，ΔT＝Ts－Tc，Ts是最大静摩擦力矩，w 为角速度。

根据实验条件，忽略ΔT，即最大静摩擦力等于滑动摩擦力。首先考虑在平板上放置一个硬币的情况，根据牛顿第一定律进行受力分析，有 f静max＝f动＝Gsinα＝μGcosα，因此，平板和硬币的滑动摩擦系数 μ1＝tanα＝tan25.5°＝0.477。放置2个硬币时，经分析可知，由于起滑瞬间角度与放置一个时始终要小，若瞬间滑动发生在硬币与平板之间，那么角度应该与之前放置1个硬币时相同，所以应该直到25.5°才滑落，故判定应该先在硬币与硬币之间发生相对滑动，对位于上面位置的硬币进行受力分析，可得硬币之间的摩擦系数为μ2＝tan21.2°＝0.388。以此类推，3个硬币及以上的情况比较复杂，初步判断应该易发生滑动的应该是从上而下倒数第二个硬币，但由于实验条件所限、硬币本身纹路不对称、偶然因素多等原因，致使起滑瞬间角度误差越来越大，平均起滑瞬间角度越来越小。

2.3 单摆大角度运动模型

单摆做微幅运动时(摆角小于5°)，属于简谐振动，单摆大角度运动作为非简谐振动，相关研究也有不少，这里以简谐振动为基础，做适当修正。简谐运动中，如图3所示，在硬币在平板上未发生相对滑动的情况下，将平板的硬币作为单摆质点在该位置进行受力分析，其中G为硬币重力，f为静摩擦力，N为平板对硬币的弹力，a为硬币此时的所受合力加速度。

根据牛顿第二定律：合力矩=外加力矩+阻尼力矩+弹性恢复力矩，此时的硬币的外合力加速度a＝-gsinθ，方向与摆杆方向垂直，指向中心位置。对运动中的硬币受力分析得以下公式：

计算得出：

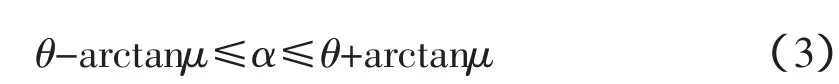
考虑2个以上的硬币的情况，取μ2，利用MATLAB仿真得到θ与α的关系图(图4)，其中θ0为起始条件，图中取最大值60°，L1是上限线，L2是下限线，L1和L2之间是稳定工作区域，为保证平板安全启动，起摆位置尽量接近安全角度21.2°，稳定平滑地转动，以及在中间平衡点稳定过渡，取L3的角度线，得：

考虑大角度单摆的周期[6]，其中l为单摆的摆长，这里取1 m。

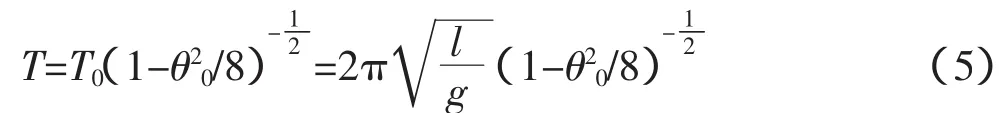
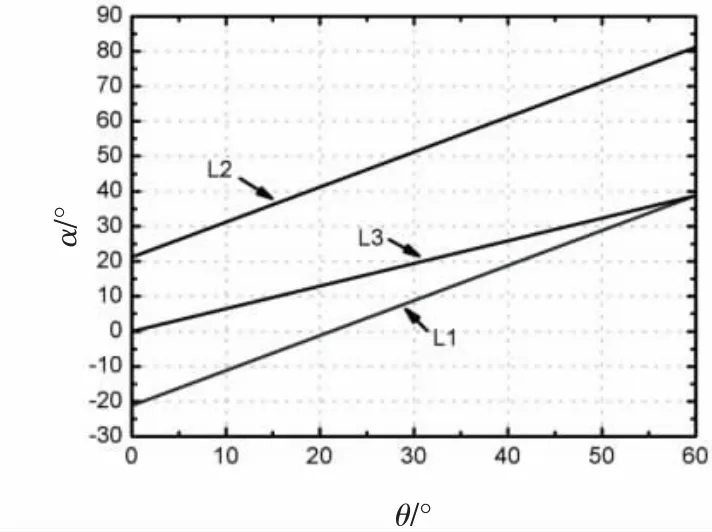
图4 θ与α的关系图Fig.4 Graph of a relation between θ and α

因此平均单位时间转动角度：

3 系统的电路实现

3.1 MCU控制模块的方案选择

系统的核心无疑是单片机部分。常见的ATMEL公司的51系列单片机软件编程自由度大，可实现各种控制算法和逻辑控制，但需外接模数转换器来满足数据采样的要求，硬件接口复杂，高速A/D与低速单片机之间速度的不匹配，给编程带来一定的难题，最重要的是其运算速度比较慢，可能无法适应该设计。

本系统采用MC9S12XS128微控制器作为控制模块。MC9S12XS128系列产品满足了对设计灵活性和平台兼容性的需求，并在一系列电子平台上实现了可升级性、硬件和软件可重用性、以及兼容性。其CPU最高总线速度40 MHz，具有64 KB、128 KB和256 KB闪存选项，均带有错误校正功能 ，带有ECC的4 KB至8 KB Data Flash，用于实现数据或程序存储，可配置8、10或12位模数转换器(ADC)，转换时间3 μs，带有16-位计数器的、8-通道定时器，出色的EMC及运行和停止省电模式。MC9S12XS128完全能够完成本设计的要求。该模块外接显示屏作为人机交换界面，显示当前所做任务。与角位移传感器链接，处理采集到的数据之后通过电机驱动模块接口后传送给电机，完成相应打角任务。

3.2 电机选取和驱动的实现

电机模块的选择是整个系统的关键所在，按照设计的要求，需要很高的精确度，并且平板需要较高的制动性。

方案一：采用普通直流电机。直流电机具有优良的调速特性，调速平滑、方便，调整范围广；对驱动芯片要求低，但是直流电机无法精确控制电机转数，并且误差将会进行叠加，在控制精度上逊于步进电机。

方案二：采用步进电机。步进电机的一个显著特点就是具有快速启停能力，另一个显著特点是转换精度高。正转反转控制灵活。相比直流电机的工作方式，步进电机是一种将电脉冲转化为角位移的执行机构。同时可以通过控制脉冲频率来控制电机转动的速度和加速度，从而达到调速的目的。

本系统采用东芝公司的TB6560AHQ二项步进电机专用驱动芯片，与采用该芯片的驱动板在电路上，结构上使用了可靠性设计，在普通散热方式的情况下可稳定的工作在3 A电流，完全可以驱动本设计中的步进电机。同时该方案可以将信号细分和电流衰减，实现最小达0.1°的步距，使得平台控制十分的平稳，该电机驱动方案也是提高减震效果的关键。

3.3 角度传感器模块

本系统采用WDY32Z-1角位移传感器，具有数据稳定性强、灵敏度高的优点。WDY32Z-1角位移传感器与摆杆相连，利用摆杆带动角度传感器转动，引起角度传感器内可变电阻的变化，使得输出端的电压发生变化，经单片机ADC端口读入并计算得出角度变化量。

系统的主控制板原理图如图5所示。

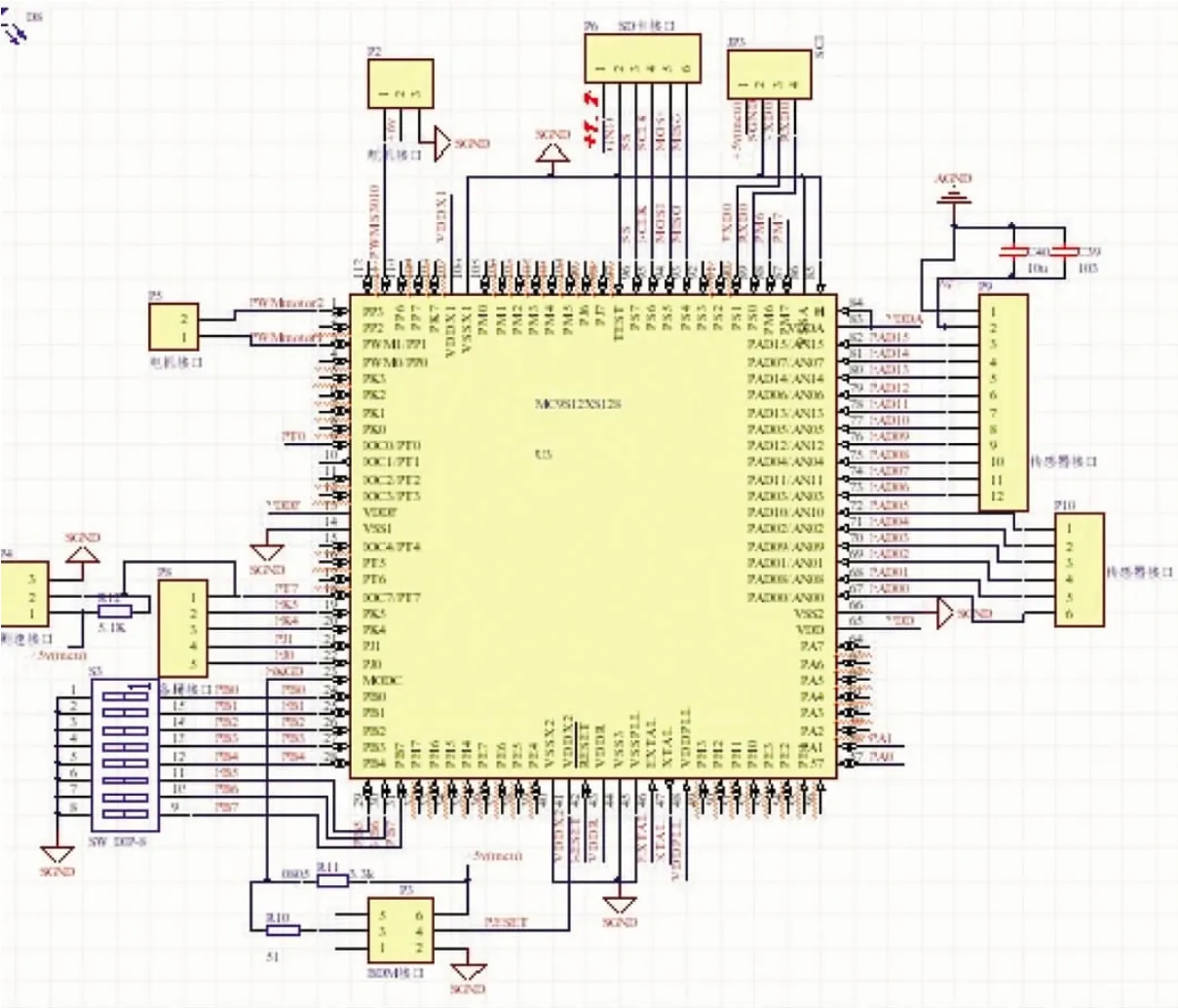
图5 主控制板原理图Fig.5 The main control board schematic diagram

4 系统的测试结果和分析

4.1 调试方案

①在量角器的协助下，将摆杆调节至下表所示的起摆位置，启动控制系统；

②松手释放摆杆，观察记录不同角度下的单摆的运行周期，与公式(5)基本一致；

③计算平均每个周期的转动角度，调节程序；

④在平板指定位置放上1枚硬币，释放摆杆，在起摆为30°～45°观察硬币相对初始位置的偏移情况，调节程序，加一个硬币再观察；

⑤调节摆杆起摆在45°～60°之间，观察平板的运动情况，逐渐增加硬币个数，最多8个，记录相应数据。

4.2 结果分析

根据表2结果分析可知：该距离表示单个或2个硬币在起摆角30°～45°时运行控制系统可基本保持稳定不动的状态，稳定性很好。

表2 硬币滑离中心距离与摆杆起摆角度θ0的关系Tab.2 The relation between θ0and the average distance sliding from the center

根据表3结果分析可知：在±50°以内成功率比较高，但是随着角度接近60°，发生哗变，这是因为理论分析中将60°作为临界角，最好设定一定的宽裕度；另外发现左右对称位置实验结果不一致，说明纸面与硬币的滑动系数不同向位置有可能有差异，且单摆的对称性也有待完善。

表3 硬币保持有效个数与摆杆起摆角度θ0的关系(8个硬币)Tab.3 The relation between θ0and the number of coins keeping still on the plate(8 coins in all)

5 结语

在整个系统实现过程中，出现了很多问题，但最终都有了妥善的处理。比如，一开始直接取，发现测试结果在约45°以上就不能保证硬币的保持个数，经过深入的分析后，采用L3的摆角关系进行控制，单摆的稳定性能有了很大的提升；单摆起摆的处理上要特别注意，平板应以约为20°附近作为静止等待工作状，启动瞬间摆置，获得加速度进而运动，这部分处理不当将出现启动即发生滑动的现象。经过系统的软硬件的多次修改调整，经测试证明，该系统能对平板角度进行精确控制，单摆大角度运动时，平板运动稳定性大大提高。

[1]程守洙,江之永.普通物理学[M].北京:高等教育出版社,1998.

[2]ROSSBERG K.A first course in analytical mechanics[M].New York:John Wiley&Sons,1983.

[3]铁摩辛柯S,杨D H,小韦孚W.工程中的振动问题[M].胡人礼,译.北京:人民铁道出版社,1978.

[4]白鸿柏,张培林,黄协清.非恒定滑动摩擦系数振动系统等效线性化计算方法研究[J].振动与冲击,2000,19(1):77-78.

[5]林复生.简明摩擦学[M].重庆:重庆大学出版社,1987.

[6]孙会娟,张 宁.大角度单摆运动的周期研究[J].北京联合大学学报:自然科学版,2006,20(4):71-73.