水下无线传感器网络节点覆盖及其自定位
2012-07-19刘玉良
张 华,刘玉良
(浙江海洋学院机电工程学院,浙江舟山 316004)
无线传感器网络应用中,重要的是监测目标的具体位置,没有确切监测消息的位置没有任何意义[1],而网络的覆盖情况则是保证网络使我们了解是否存在监测和通信盲区,了解被监测区域的无线传感器网络的覆盖情况,从而重新调整传感器节点分布或者指导在将来添加传感器节点时可采取的改进措施。以通过调整网络覆盖的密度,对被监测区域中重要区域设置热点,部署更多的传感器节点,保证测量数据的可靠性[2-4]。按照定位过程中是否需要测量节点之间的实际距离,把定位算法分为,基于距离的定位算法和距离无关的定位算法。
水声通信网络的研究起步于20世纪90年代。美国计算机学会从2006年开始成立了国际工作组,专门开展水下声传感器网络的研究和交流。美国多所大学,包括麻省理工、乔治亚理工等都成立水下声传感器网络课题组开展专门的研究工作[5-9]。国内,水声传感器网络方面的研究也才刚刚开始,2006年,中科院声学所、哈尔滨工程大学、北京科技大学等研究单位在863计划的支持下,结合多年水声通信的研究经验,开展水下声传感器网络的相关研究[10-12]。
从现有的文献来看,对水声无线传感器网络节点覆盖及自定位的问题开展比较少。笔者主要研究水下传感器网络二维情况下节点覆盖及其自定位问题,采用概率感知模型研究如何提高节点覆盖概率,在此基础上,探讨节点自定位问题,再采用遗传算法对节点的覆盖与自定位进行优化,从而实现节点覆盖及其自定位的优化控制。
1 问题描述及数学模型
从现有的文献和研究[13-18]来看,无线传感器网络以随机抛洒形式分布的节点一般有:均匀分布、高斯分布、瑞利分布等,其中以高斯分布最常见。在实际应用环境中,由于环境噪声干扰以及信号强度随传输距离衰减,传感器节点的检测能力表现出一定的不确定性,概率感知模型反映了这种不确定性。在概率感知模型中,某传感器节点x检测到任意点P处发生的事件的概率为:
假设监测区域xlength×ylength,其中xlength,ylength分别是该坐标对象的横坐标长度和纵坐标长度,随机布撒一定数量的节点作为信标节点,各个节点坐标通过相互通信或者位置等信息,各节点坐标分别为P(ixi,y)i,(i=1,2,…,n),随机布撒若干未知节点,未知节点坐标为X(jxj,y)j,(j=1,2,…,m),该节点与各信标节点的距离分别为di,( i=1,2,…,n);同时,此监测区域被数字离散化为若干个像素(像素主要指信标节点),像素点坐标为(x,y),则目标像素点与未知传感器节点的距离素点被传感器节点所覆盖的事件定义为ni,则该事件发生的概率P(n)i即为像素点(x,y)被传感器节点Ni所覆盖的概率[19-20]:

实际上由于监测环境和噪声干扰,传感节点测量模型应呈一定特性的概率分布,即:

其中,re(0<re<r),α1,α2,β1,β2,是与传感节点特性有关的测量参数,λ1,λ2为输入参数:

为提高目标测量概率,需采用多个传感节点同时测量目标。联合测量概率如下:

其中,Nov为测量目标的传感节点集合。由于实际中存在测量误差,节点间的测量距离跟坐标距离之间存在误差值,该节点与各信标节点的测距误差分别为δi,(i=1,2,…,n);根据上述问题描述,按欧式距离建立该未知节点X(xest,yest)和与其通信的各信标节点之间建立方程组如下,

公式(5)以未知节点和信标节点间的距离作为约束力,制约了未知节点坐标的范围,若传感器节点处于理想状况之下,左侧结果都应为0,故各误差值之和越小越趋向于理想状态,即:
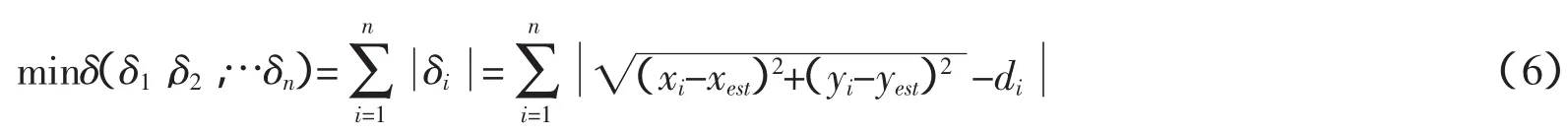
未知节点要测算自身的最佳位置问题可以转换成寻找公式6中绝对值的和最小值。
2 遗传算法原理及设计
2.1 遗传算法及算子
遗传算法是模仿了生物的遗传进化机制进行自然选择和遗传的一种寻优算法,具有简单、精度高等特点,广泛应用于人工智能、神经网络等领域。在遗传算法中,算子的选择至关重要,包括选择选择算子,交叉算子,变异算子,其中交叉算子决定了该算法的全局搜索最优解能力,变异算子则决定了算法的局部搜索最优解的能力[15]。各遗传算子的选择如下:
选择操作建立在对个体的适应度进行评价的基础之上,适应度较高的个体被遗传到下一代的概率较大,适应度较低的个体被遗传到下一代的机会较少,从种群中使用随机遍历抽样方式选择适应度较高的个体,选择的概率取GGAP。已知的交叉操作主要包含了交叉点的位置和如何交换部分基因的方式。本文采用算术交叉,算术交叉(Arithmetic Crossover)是指由两个个体的线性组合而产生出两个新的个体。设有父代两个个体g1,g2,进行交叉后将得到两个子代g1,g2,表达式分别是:

α也可以是一个由进化代数所决定的变量(此时,所进行的交叉运算称为非均匀运算)。算术交叉的主要操作过程为:首先确定两个个体进行线性组合时的系数α;根据上述公式生成两个新的个体;交叉概率为Pc。变异算子是产生新个体的辅助方法,决定了遗传算法的局部搜索能力。设s=(v1,v2,…vn)是一个父代解,其中分量 vi被选择为进行变异,其定义区间为[ai,bi],则变异后的父代解为 s′=(v1,v2,…vi-1,vi+1,…vn),其中可表示为:

这里,“0”,“1”代表变异的方向,γ 是在区间[0,1]的随机数,k 是系数,范围在 0~1 之间,random 是随机产生0和1。其中,(T,y)=y(1-γT2),T代表最大代数。变异概率取Pm。
2.2 遗传算法实现及步骤
2.2.1 位置获取及覆盖控制
在第1阶段,首先是所有节点初始化,信标节点获知自身各类信息,并自动向外广播自身位置信息,未知节点接收后,保存并将该信息转播一次;在第2阶段,信标节点(像素点)根据所获知的信息对覆盖区域内的所有未知节点进行覆盖测算,以获取未知节点能够被覆盖并定位的可能性,进而将所获得信息转发至周围能够通信的未知节点;在第3阶段,未知节点根据转发的信息,根据覆盖概率的大小,决定是否进行定位(本文设置覆盖概率大于等于80%的未知节点能够进行有效定位);在第4阶段,能够进行有效定位的节点,根据节点的定位算法,进行定位;第5阶段,自行进行迭代计算的定位算法的进化过程比较慢,并且精度不太高,因而用遗传算法对未知节点进行优化计算,优化计算过程包括初始化种群,选择操作,变异操作和交叉操作,还包括计算停止条件。
2.2.2 算法步骤
步骤1,所有节点初始化,信标节点向外广播自身信息,未知节点获取信息后保存并转发一次;
步骤2,信标节点根据所获知信息,采用公式2对单个节点进行覆盖计算(在实际算法中,可采用公式4对多个节点进行联合覆盖计算);
步骤3,未知节点根据指令,自动剔除覆盖率过低的未知节点,覆盖率较高的未知节点进入定位程序计算;
步骤4,采用遗传算法,根据未知节点给定信息对种群进行初始化设计,给出符合运算的二进制种群;
步骤5,根据二进制种群,依据定位公式5,进行选择操作,并设定选择概率;
步骤6,依据公式7实现交叉操作,并设置变异率的参数;
步骤7,依据公式8实现变异操作,并设置交叉率的参数;
步骤8,根据定位指标设置遗传算法精度,根据算法精度要求观察步骤7的结果是否符合要求,不能达到精度要求,转到步骤5,重新进行迭代运算;如果达到精度要求,则转入步骤9;
步骤9,输出结果,整体覆盖概率以及定位参数等,程序运行结束。
3 仿真结果与分析
在100×100范围内布置30个信标节点,10个未知节点,取个体数目为40个,遗传迭代次数为25次,代沟取0.9,变异概率取0.3,交叉概率取0.7。采用主频为3G的计算机,在matlab7.0.1环境下进行仿真。
图1 节点初始化覆盖状况Fig.1 Cover condition of node initialization

图2 迭代次数与覆盖率Fig.2 The number of iterations and coverage

图3 覆盖率与感知半径Fig.3 Coverage and perception radius
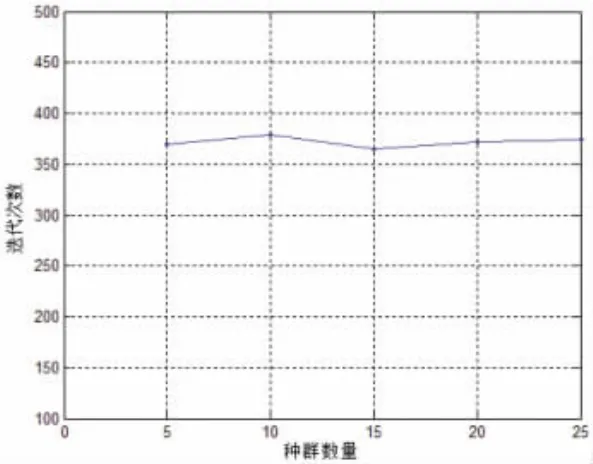
图4 迭代次数与种群数量Fig.4 The number of iterations and population

图5 信标节点密度与定位误差Fig.5 Position error and density of anchor nodes

图6 均值和最优解分布Fig.6 Distribution of mean and the optimal solution
图1表示水下传感器节点初始化分布图。现有文献研究[19]表明传感器节点的初始分布对节点的覆盖概率影响不大。图2表示算法的迭代次数与未知节点的覆盖概率的关系,表明迭代次数较少时,覆盖概率不高;当迭代次数达到一定程度时,覆盖概率不受迭代次数影响。图3表示的是覆盖概率与感知半径之间的关系,感知半径越大,未知节点接受到信标节点的信息越多,因而受到覆盖的可能性也越大;当感知半径达到一定数值以后,对覆盖概率影响不大。图4表示迭代次数与初始的种群数量之间的关系,从图中可以看出,种群数量对迭代次数影响不大。图5表示信标节点密度与节点自定的误差之间的关系,表明当信标节点密度较低时,定位误差很大,当信标节点密度在不断增加时,定位误差的精度在不断降低,图中数据表明,当信标节点的密度达到35%以后,定位精度受此影响几乎不会改变。图6表示定位过程中,节点自定位的误差的均值以及最佳解,从图中可以看出,当迭代次数在不断增加时,节点定位误差在不断减少,从而提高整体定位精度。
4 小结
水下传感器网络是海洋战略中重要的一环,节点覆盖及其自定位则是水下传感器网络的关键技术之一。本文采用概率感知模型对节点进行覆盖计算,再对覆盖概率较高的节点进行自定位,最后采用遗传算法进行定位精度寻优迭代。仿真表明,迭代次数对未知节点的覆盖概率有较大影响;感知半径越大,覆盖概率越高,当半径达到一定程度后,对覆盖概率影响有限;信标节点的密度的高低影响节点自定的精度。总而言之,遗传算法能够有效的对水下传感器节点覆盖及其自定位进行优化。
[1]孙利民,李建中,陈 渝,等.无线传感器网络[M].北京:清华大学出版社,2005.
[2]BULUSU N,HEIDEMANN J,ESTRIN D,et al.Density adaptive algorithms for beacon placement in wireless sensor networks[C]//IEEE ICDCS’01(Phoenix,AZ).2001.
[3]HE Tian,HUANG Cheng-du,BLUM B M,et al.Range-Free Localization Schemes in Large Scale Sensor Networks[C]//Proceedings of the 9th Annual Inter2 National Conference on Mobile Computing and Networking(MobiCom).San Diego,California,USA:ACM Press,2003:81-95.
[4]PATWARI N,ASH JN,KYPEROUNTAS S,et al.Locating the nodes:cooperative localization in wireless sensor networks[J].Signal Processing Magazine,IEEE,2005,22(4):54-69.
[5]田金鹏.无线传感器网络节点定位技术研究[D].上海:上海大学,2009.
[6]周 全,朱红松,徐勇军,等.基于最小包含圆的无线传感器网络定位算法[J].通信学报2008,29(11):84-90.
[7]蒋 杰,方 力,张鹤颖,等.无线传感器网络最小连通覆盖集问题求解算法[J].软件学报,2006,17(2):175-184.
[8]李兆斌,魏占祯,徐凤麟.无线传感器网络增强的质心定位算法及性能分析[J].传感技术学报,2009(4):563-566.
[9]MAO Guo-qiang,FIDAN B,ANDERSON B.Wireless sensor network localization techniques[J].Computer Networks,2007,51(10):2 529-2 553.
[10]LANGENDOEN K,REIJERS N.Distributed localization in wireless sensor networks:a quantitative comparison[J].Computer Networks,2003,43(4):499-518.
[11]曹正文,赵 健,高宝建.基于加权最小二乘法的红外多站定位的研究[J].光子学报,2005,34(7):1001-1004.
[12]CARDEI M,Du Ding-zhu.Improving wireless sensor network lifetime through power aware organization[J].ACM Wireless Networks,2005,11(3):333-340.
[13]程铭东.基于遗传算法的多传感器网络中目标定位算法[J].计算机工程与应用,2008,44(16):105-107.
[14]YI.Zou,KRISHNENDU CHAKRABARTY.Sensor Deployment and Target Localization in Distributed Sensor Networks[J].ACM Transactions on Embedded Computing Systems,2004,3(1):61-91.
[15]NICULESCU D.Positioning in ad hoc sensor networks.Network[J].IEEE,2004,18(4):24-29.
[16]曹 峰,刘丽萍,王 智.能量有效的无线传感器网络部署[J].信息与控制,2006,35(2):147-153.
[17]RICE J.Telesonar signaling and Seaweb underwater wireless networks[J].New Information Processing Techniques for Military Systems,2001,(17):1-13.
[18]ANGELINE P J.Using Selection to improve Particle Swarm Optimization[R]//Proceedings of the IEEE Congress on Evolutionary Computation,ICEC,1998:84-89.
[19]张文爱,刘丽芳,李孝荣.基于粒子进化的多粒子群优化算法[J].计算机工程与应用,2008,44(7):51-53.
[20]WANG Xue,WANG Sheng,MA Jun-jie.Dynamic deployment optimization in wireless sensor network[J].Lecture Notes in Control and Information Science,2006,344:182-187.
