含有不可控变迁的Petri网死锁避免策略

吴国凤， 胡德启， 安 磊， 郑礼良

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

含有不可控变迁的Petri网死锁避免策略

吴国凤， 胡德启， 安 磊， 郑礼良

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

文章针对Petri网建模的并发系统中的死锁问题，利用Petri网可达树分析方法检测系统死锁的存在，结合Petri网控制器的设计来达到预防和避免死锁的目的；提出了一种新的约束设计思想，进行控制器设计，使得系统不会出现死锁；更进一步地考虑到控制器设计过程中存在不可控变迁的情况下系统避免死锁的设计问题。

Petri网；控制器；混合约束；死锁

并发进程的死锁问题是分布式系统中的一个重要研究课题［1］。在多个并发进程系统中，如果每个进程持有某种资源，同时又等待其他进程所持有的各种资源，此时，每个进程都持有一定资源但又都无法推进，这样就形成了死锁［2］，这样的死锁在分布式系统中时有出现，因此，发现和提出好的死锁检测、预防和解除方法尤为重要。

文献［3］提出了基于库所不变量的控制器设计算法，该方法利用整个Petri网的关联矩阵来计算控制器，计算的复杂度比较大，而且只适用于安全网。文献［4］提出了Parikh向量不等式的约束转换算法，再用基于库所不变量的控制器算法设计控制器。但是，以上各种方法并没有把控制器算法应用于解决Petri网的死锁问题。

本文在总结上述控制器设计算法时存在问题和研究Petri网建模的并发系统中的死锁问题基础上，利用Petri网可达树分析方法检测系统死锁的存在，设计出一种可以避免死锁的约束条件，结合Petri网控制器的设计来达到预防和避免死锁的目的［5－6］。

1 基本知识

1.1 动态死锁

定义1 Petri网系统Σ＝（S，T；F，μ0），如果存在标识μ∈R（Σ，μ0），对任意的一个变迁t∈T，状态函数δ（μ，t）无定义，那么则称标识μ为死锁标识［2］。

定义2 Petri网系统Σ＝（S，T；F，μ0），如果可达标识集合中存在死锁标识，那么Petri网中存在死锁［2］。

定理1 分布式并发进程中存在死锁，且仅当其Petri网模型的可达树中存在死标识。

动态死锁反映了Petri网系统的动态运行特征，如果Petri网系统发生死锁，那么该Petri网的可达标识集合中一定有与之相对应的死标识。因此，Petri网的动态死锁问题就可以归结为Petri网的可达标识集合中是否有死标识的问题。

1.2 线性不等式约束

线性不等式约束是Petri网控制器构建的前提，对于实际系统，结合控制要求，往往能将控制要求转变为一个不等式或不等式组。

一般的线性不等式又叫单纯的标识约束，它的约束形式为Lμ≤b，其中，L∈；μ∈Zn×1；b∈；n为 Petri网中的库所数；nc为不等式约束的个数。

混合约束同一般的线性不等式约束相比有更强的描述能力，它是指标识约束和变迁激发约束同时存在的约束，约束形式为C＝Lrμr＋λrqr≤b。其中，qr是第r个变迁的激发索引，当qr＝1时，就表示第r个变迁tr被激发；λr∈；nr为约束变迁的个数；nc为约束条件的个数。这种不等式约束称为混合约束。

2 存在不可控变迁的Petri网死锁避免策略

2.1 死锁检测算法

根据Petri网可达标识树的生成算法［7］，对输出结果稍作修改，就可以输出在死标识状态下含有死标识的库所集。

设库所si对应于标识μi，在死标识μi状态下含有死锁标识的库所集Mi＝｛s1，…，sk｝和死标识数目ai，死标识集合DM＝∅，与之对应的Mi的集合DS＝∅。

（1）以库所si为头结点，如果系统出现死锁，那么μi就为一个死锁标识，输出｛μi；Mi；ai｝，执行步骤（2）；否则执行步骤（3）。

（2）重新选择一个库所，如果是重复节点，执行步骤（3）；否则执行步骤（1）。

（3）库所sj为重复节点，如果选定库所si，它的其中一个输出变迁可以激发而产生的库所为sj，那么令si＝sj，执行步骤（1）。

重复执行步骤（1）～（3）。

该算法得到DM＝｛μ1，…，μn｝，DS＝｛M1，…，Mn｝和A＝［a1，…，an］T。由于含有死锁标识的库所集DS＝｛M1，…，Mi｝中可能存在重复向量，要对该库所集简化，从而可以得到一个新的含有死标识的库所集DS′＝｛M1，…，Ml｝。

2.2 构造混合约束

利用上述的死锁检测算法，可以得到在死标识状态下含有死标识的库所集和死标识数目。构造库所约束条件的主要思想是：只要在死标识状态下含有死标识库所中的标识数目之和小于该死标识总数，就可以得到一个关于约束库所的约束条件，即Ci＝∑si≤ai－1，其中si是在标识μi状态下含有死标识的库所。这样就构造出一个库所约束条件C＝Lrμr≤b。它的意义是如果这些库所中的标识数目之和不能大于或者等于死锁标识数时，那么该系统一定出现了死锁。则库所约束条件为：

其中，b＝min｛a1－1，…，ai－1｝。

通过对Petri网系统的基本性质和运行规律进行分析和总结，不难得到产生死锁的4个必要条件，即互斥、占有等待、不剥夺、环路等待。构造变迁约束条件的主要思想是：选取的约束变迁对应着库所约束条件，使变迁不能同时激发，达到无死锁状态，即在变迁约束条件C＝λrqr≤c下，死锁不能出现。不难看出，上述约束条件不是唯一的，只要破坏其中一个必要条件，系统就会无死锁。则变迁约束条件为：

因此，根据上述库所约束条件和变迁约束条件写出混合约束，即

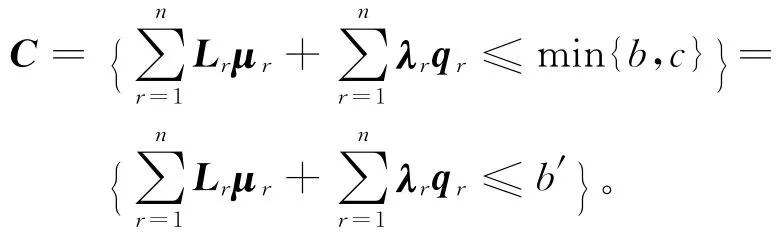
2.3 含有不可控变迁的控制器设计方法

如果一个变迁的激发不能通过外部的行为进行禁止，那么则称该变迁为不可控变迁。因为不可控变迁只能由受控Petri网的结构和状态来决定，与外部环境无关，因此，如果Petri网系统中存在不可控变迁，需要对不可控变迁进行等价变换才能对控制进行设计，使得系统无死锁。

给定一组约束，而且Petri网系统中存在不可控变迁，控制器可能会禁止不可控变迁的激发，那么则称该约束为禁止约束，反之称为允许约束。禁止约束必须要转化为允许约束，才能计算控制器［8－9］。

2.4 不可控变迁的转换

对形如C＝Lrμr＋λrqr≤b的混合约束转换，有如下2种算法。

2.4.1 算法1

（1）对约束条件进行约束转换，转化形式为Lrμr≤k和λrsr≤b－k，其中k∈［0，b］。

（2）检测约束的允许性，即是否满足条件LDuv≤0，其中Duv为关联矩阵与不可控变迁的相关子集。如果该约束条件成立，那么该约束条件是允许约束，就不需要处理，直接进行控制器设计；否则，执行步骤（3）。

（3）如果LDuv＞0，那么它就为禁止约束。可以将Lrμr≤k转化为一个允许约束，即L′μr≤k，使得L′Duv≤0成立，从而得到一个新的允许约束：C′＝L′μr＋λrqr。

通过矩阵变换的方法求新的系数方程L′，设

其中，I为对角矩阵，M（i，j）表示矩阵M中的第（i，j）个元素，令j＝1。

2.4.2 算法2

（1）若M（k＋h＋1…k＋h＋nc，j）中存在M（s，j）＞0，执行步骤（2）；否则，令j＝j＋1，重新执行步骤（1）。

（2）若M（1…k＋h，j）中不存在M（s，j）＞0，则不能设计出合法的控制器；否则找出min（｜M（k＋h＋1…k＋h＋nc），j｜），满足M（q，j）＜0，执行步骤（3）。

（3）如 果｜M（q，j）｜≥M（s，j），则 执 行M（s，·）＝M（s，·）＋M（q，·）；否则执行d＝floor（M（s，j）／｜M（q，j）｜）。

如果 mod（M（s，j），M（q，j））＝0成立，那么M（s，·）＋dM（q，·），否 则M（s，·）＝M（s，·）＋（d＋1）M（q，·）。

（4）重新执行步骤（1），一直到M（k＋h＋1…k＋h＋nc，j）中不存在M（s，j）＞0；这时，M矩阵变换为：

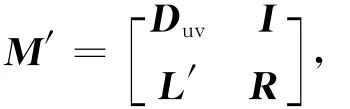
从而得出L′＝R＋Lr。

2.5 避免死锁的控制器设计步骤

为了更好地设计控制器，作如下假设：Petri网中存在引发死锁变迁中某个或者某些变迁为不可控变迁；Petri网模型中无自环。

算法步骤如下：

（1）确定约束库所Cs和约束变迁Ct。

（2）根据约束条件写出约束库所的局部关联矩阵D0和系数矩阵L，为了进行约束转换，把D0扩展为：

其中，h≥0，sm，…，sm＋h为与不可控变迁相关联的非约束库所。

（3）判断约束的允许性，即是否满足LDuv≤0。如果满足条件就是约束条件，令L′＝L，执行步骤（5），否则执行步骤（4）。

（4）用等价变换的约束转换算法把禁止约束转化成新的允许约束：C′＝L′μr＋λrqr。

（5）控制器库所的局部关联矩阵为：Dc＝－Lr′D0。

（6）对控制器库所的局部关联矩阵Dc增加约束变迁行tr，在tr行中对应约束变迁的位置上填写1，其他位置写0，即

对控制器的增广局部关联矩阵Dc′中的元素分布情况，可以根据以下规则构建控制器库所与变迁之间的流关系和权值：① 如果在约束变迁tr的元素1对应着矩阵sc行的元素大于0，那么在控制器库所sc与该变迁之间构建一条双向弧，控制器库所sc是该变迁的输出库所；② 如果在约束变迁tr的元素1对应着矩阵sc行的元素小于等于0，那么就在控制器库所sc与该变迁之间构建一条流关系，即控制器库所是该变迁的输入库所；③ 如果在约束变迁tr的元素0对应着矩阵sc行的元素小于0，那么在控制器库所sc与该变迁之间构建一条流关系，即控制器库所是该变迁的输入库所；④ 如果在约束变迁tr的元素0对应着矩阵sc行的元素大于等于0，那么在控制器库所sc与该变迁之间构建一条流关系，即控制器库所是该变迁的输出库所；⑤当一个变迁激发导致约束中的标识数目减少时，就让控制器库所成为不可控变迁的输入库所的输入变迁的一个输入库所。反之，控制器库所成为该变迁的一个输出库所的输出变迁的输入库所，以此来保证所有库所中的标识数目不变。

（7）计算控制器库所增广的初始标识：μc0＝b′－L′μr0。

2.6 控制器设计的复杂性分析

本文采用的不可控变迁的约束转换算法，与C－变换的约束转换算法相比，不需要建立中间模型，并且用线性拆分和线性组合的方法代替C-变换和C－逆变换2个过程来进行约束转换。该算法用不等式计算，不需要进行矩阵计算，大大减少了计算的复杂度和难度。本文中的控制器设计算法用局部关联矩阵代替关联矩阵，结合局部设计原则设计控制器，随着系统的规模变大和结构更复杂，控制器设计时的计算量大大减少。

3 应用举例

一个并发系统的简单的Petri网系统，如图1（实线部分）所示。

图1 含有不可控变迁的Petri网预防死锁的系统模型

该网系统存在死锁，利用2.1所述算法，可以得到该Petri网系统模型的死锁标识集合DM＝｛μ2，μ7｝、在死锁标识μ2和μ7状态下含有死锁标识的库所集都为M＝｛s2，s8｝和死锁标识数目a＝2。因为在死锁标识μ2和μ7产生时，含有死锁标识的库所集都为M＝｛s2，s8｝，所以DS中只有一个向量。因此，可以构造一个库所约束条件为：

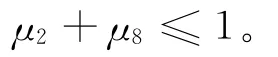
分析死锁产生的原因，只要变迁t1和t7同时不能发生时，该系统就不会出现死锁。因此，可以构造一个变迁约束条件为：

可以根据库所约束条件和变迁约束条件，构造出混合约束为：

其中，约束库所为Cs＝｛s2，s8｝；约束变迁为Ct＝｛t1，t7｝。

要想避免死锁，就要在不等式约束μ2＋μ8＋q1＋q7≤1条件下设计控制器。假设t2为不可控变迁，设计控制器来实现下面的混合约束，使得该Petri网不会出现死锁［10－12］。

构建局部关联矩阵D和系数矩阵Lr：

由于t2为不可控变迁，所以Duv＝［－1，1，0］T。

因为LrDuv＝1＞0，则要进行约束转换。令

经过变换后得到一个矩阵：

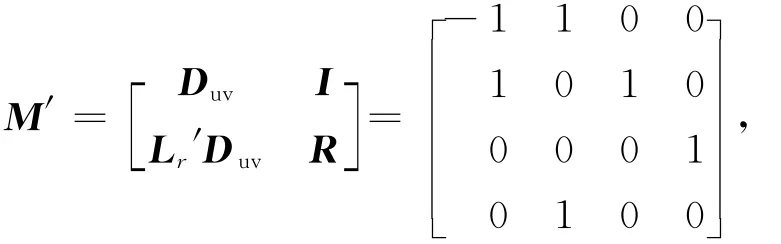
从而可以得到：

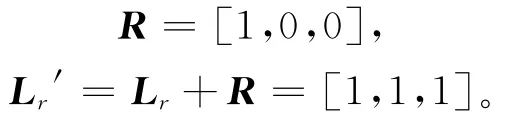
因为已经把禁止约束转化为允许约束，所以可以得出一个新的约束条件，即

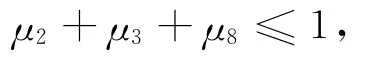
从而可以得出控制器库所的局部关联矩阵：

控制器库所的局部增广关联矩阵：

利用控制器库所构建流关系的规则，来构建控制器库所与之相连的变迁的流关系。同时求解出控制器库所的初始标识数目：

由图1可见，sc为控制器库所，虚线部分为控制器与相关变迁之间的流关系。

利用本文中改进的可达标识树死锁检测算法进行验证，得到DM＝∅，DS＝∅，｜A｜＝0。从而可以得出增加一个控制器库所sc所得的Petri网就变成一个活网，死锁检测和预防过程完毕。

4 结束语

本文通过死锁检测算法检测出死锁标识和对应的库所集，构造库所约束，结合产生死锁的必要条件构造变迁约束，从而得出一个混合约束。利用约束条件设计控制器，避免死锁的发生。在文献［13］的基础上，考虑在Petri网中存在不可控变迁的情况下，提出了预防和避免死锁的解决方法。通过线性不等式的等价转换把禁止约束转化为允许约束，得出新的约束条件，然后再设计控制器，达到预防和避免死锁的目的。同时，本文在已给出的死锁检测方法的基础上，采用了局部设计的原则设计控制器来预防和避免死锁。由于只考虑与约束变迁和不可控变迁相关的库所和变迁，使得计算量大大减少。

［1］毕 翔，韩江洪，王跃飞，等.面向PLC的离散事件控制系统设计方法研究［J］.合肥工业大学学报：自然科学版，2010，33（9）：1333－1337.

［2］吴哲辉.Petri网导论［M］.北京：机械工业出版社，2006：88－91.

［3］Moody J O，Antsaklis P J.Petri net supervisors for DES with uncontrollable and unobservable transitions［J］.IEEE Transactions on Automatic Control，2000，45 （3）：461－477.

［4］Iordache U V，Antsaklis P J.Synthesis of supervisors enforcing general linear constraints in petri nets［J］.IEEE Transactions on Automatic Control，2003，48（11）：2036－2039.

［5］林 闯.随机Petri网和系统性能评价［M］.北京：清华大学出版社，2000：67－71.

［6］王卫红.建模与仿真［M］.北京：科学出版社，2002：74－76.

［7］Cui Huangqing，Wu Zhehui.PMI programs’petri net model and its dynamic properties［J］.Journal of System Simulation，2006，18（9）：2455－2460.

［8］Tanenbaum A S.Distributed operating system［M］.北京：清华大学出版社，1997：58－60.

［9］Han Yaojun，Wu Zhehui.Petri net－based serializability and deadlock detection in concurrency control of database［C］／／第十七届全国数据库学术会议论文集.河北保定：河北大学出版社，2000：104－106.

［10］Xing K Y，Tian F，Yang X J.Optimal deadlock avoidance petri net supervisors for automatic manufacturing system［J］.Journal of Control Theory and Applications，2007，5（2）：289－295.

［11］卢 超，卢炎生，谢晓东，等.一种基于依赖分析的并发程序潜在死锁检测算法［J］.小型微型计算机系统，2007，28（5）：841－844.

［12］周之英.现代软件工程［M］.北京：科学出版社，2001：98－99.

［13］Yamalidou K，Moody J O，Lemmon M，et al.Feedback control of petri nets bases on place invariants［J］.Automatica，1999，32（1）：15－28.

Avoiding deadlock with uncontrollable transition in Petri net

WU Guo－feng， HU De－qi， AN Lei， ZHENG Li－liang
（School of Computer and Information，Hefei University of Technology，Hefei 230009，China）

To solve the deadlock problem of the distributed system in Petri net，this paper proposes a method to detect the deadlock by the analysis of the reachable marking tree and prevent it by the design of the Petri net controller.And a new view of mixed constraints is presented for the controller design.Furthermore，how to avoid deadlock in the circumstance of the uncontrollable transition with the design of Petri net controller is studied.

Petri net；controller；mixed constraint；deadlock

TP399

A

1003－5060（2012）04－0472－05

10.3969／j.issn.1003－5060.2012.04.009

2011－03－14；

2011－04－20

国家自然科学基金－广东联合基金重点资助项目（U1135003）

吴国凤（1954－），女，安徽合肥人，合肥工业大学副教授，硕士生导师.

（责任编辑 吕 杰）