基于模糊Petri网的数控机床主轴故障诊断*

申桂香 王志琼 张英芝 李全普 谷东伟 李怀洋

(①吉林大学机械科学与工程学院，吉林长春 130022;②大连机床集团有限责任公司，辽宁大连 116620)

主轴是数控机床的关键功能部件，其故障将导致数控机床的故障，甚至停机［1］。因此，研究主轴的可靠性是十分必要的。以往对于主轴的可靠性研究，多采用故障树分析、FMECA分析，可靠性评价等［2］。有时主轴的可靠性很高，但其可用性却很低，造成这种现象的主要原因是主轴结构复杂，出现故障后需要花很多时间进行故障诊断，查找导致故障的根本原因。模糊Petri网通过模糊推理规则，有效地解决了这一难题［3－4］。

Petri网是1962年由德国Bonn大学Petri.C.A提出的，是一种能够系统地描述数学和图形的分析工具，具有可达性、安全性、可逆性、有界性等性质［5］。相对于故障树，Petri网更能动态地描述各种故障状态之间的因果关系［6］。模糊Petri网在Petri网的基础上增加了模糊推理规则［7］。近年来，模糊Petri网在可靠性方面应用较为广泛，在汽车、航天、船舶等领域都有所研究［8－10］。但是基于模糊Petri网的故障诊断仅考虑变迁的可信度，还是会显得较为片面［11－12］。本文综合考虑变迁的可信度和激发频率，提出了改进的模糊Petri网的故障诊断方法。结合此思想，运用改进的模糊Petri网对数控机床主轴进行故障诊断，既考虑了导致主轴故障的可信程度，又考虑了导致主轴故障的频率，相对于其他方法，可更加快速，精确地进行故障诊断，减少维修时间，提高主轴的可用性，对于数控机床整机可用性的提高有很大的帮助。

1 模糊Petri网的定义

定义模糊Petri网为一十元组:

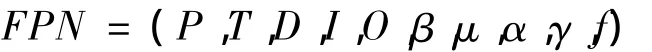
其中各字母的含义如下:P为库所有限集合，P={p1，p2，…，pm}(m ＞0);T 为变迁有限集合，T={t1，t2，…，tn}(n＞0);D 为命题有限集合，D={d1，d2，…，dm};I为P→T的输入函数;O为T→P的输出函数;β为库所与命题之间的映射，即 β(pi)=di，pi∈P，di∈D，表示命题pi的真实程度为di;μ为变迁的可信度函数，即μ(ti)=μi，μi∈［0，1］，表示变迁 ti的可信度为 μi;α 为库所的可信度函数，即 α(pi)= αi，αi∈［0，1］，表示库所pi的可信度为αi;γ为变迁的频率函数，即γ(ti)=γi，γi∈［0，1］，表示变迁 ti激发的频率为 γi;f为变迁逆向激发值函数，f(ti)=μi× γi，f(ti)∈［0，1］。

在FPN模型中，用“○”表示库所，“▎”表示变迁，库所与变迁之间用有向弧“→”连接，“○”中的“·”代表库所pi的一种状态，称为托肯(Token)。托肯在模糊Petri网中的移动直观地表示了系统的动态过程。常见的FPN模型主要有以下3种形式，如图1所示。若库所为起始库所，则pi的可信度为 μ(ti)= μ′i，μi是由用户给予的β(pi)=di的命题的真实程度;若库所为中间库所或最终库所，则可信度的计算如图1所示。

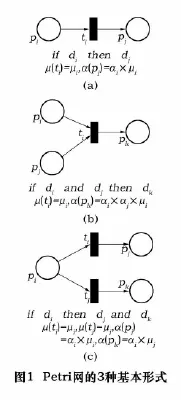
2 故障诊断FPN的模糊推理规则

2.1 库所的模糊性

在故障诊断FPN中，库所表示故障的行为和状态。库所分为以下三类:

(1)只有T→P，没有P→T的库所称为故障现象库所，对应的命题表示故障发生的现象;

(2)既有T→P，又有P→T的库所称为故障部位库所，对应的命题表示故障发生的部位;

(3)只有P→T，没有T→P的库所称为故障原因库所，对应的命题表示故障发生的根本原因。故障原因对应命题的真实程度叫做库所的可信度，具有一定的模糊性，根据专家经验取值。

2.2 变迁的模糊性

变迁表示输入库所与输出库所对应命题之间的关系，在故障诊断中，代表前一故障导致下一故障的过程。变迁的可信度表示前一故障能够导致下一故障的程度。模糊Petri网模型的3种形式如图1所示。若已知故障原因或故障部位的可信度，根据Petri网模型的形式，以及变迁的可信度，就可运用3种基本形式对应的公式求得故障部位库所或故障现象库所的可信度。变迁的激发频率在故障诊断中代表零部件发生故障的频率，具有不确定性，根据观测样本的统计特性和专家经验决定故障发生的频繁性。

2.3 逆向激发冲突的消除

传统FPN中，max(μ)所在的库所优先诊断。根据实际经验，max(γ)所在的库所应该优先诊断。由此产生冲突，max(μ)所在的库所对应的γ小，而max(γ)所在的库所对应的μ小，难以确定优先顺序。本文引入逆向激发值的定义，取max(f)对应的库所优先诊断，消除了逆向激发的冲突。

2.4 故障诊断的模糊推理策略

故障诊断的模糊推理过程主要分为逆向推理和正向激发两部分。

(1)逆向推理

列出各个库所的可达性集合和立即可达性集合［14］，库所pi可达性集合为库所pi经过一系列变迁所得到的库所的集合，库所pi的立即可达性集合为库所pi只经过一次变迁所达到的库所的集合。将故障现象库所pi作为目标，以故障现象库所pi为立即可达集的所有库所中，优先诊断最大逆向激发值对应的库所，如果该库所为故障原因库所，逆向推理结束。如果该库所为故障部位库所，重新将故障部位库所作为目标继续逆向推理，直到逆向激发得到的库所为故障原因库所。

(2)正向激发

在故障诊断的故障原因库所放置一个托肯(Token)，表示该库所对应的命题存在。工作人员检查逆向推理得到的故障原因，判断故障原因的真实程度，给予故障原因库所可信度，然后判断变迁是否可以激发。输入库所表示变迁激发的前提条件，输出库所表示变迁激发导致的结果。给定每个变迁固定的阈值λ。当α(pi)≥λ，变迁激发，托肯转移到变迁激发的输出库所中，如果输出库所为故障现象库所，说明故障原因已经找到;如果输出库所为故障部位库所，继续进行激发，直到故障现象库所。当α(pi)＜λ，变迁无法激发，对模糊Petri网其他故障部位和故障原因库所进行逆向推理，重新诊断。

3 基于FPN的数控机床主轴故障诊断实例

本文以文献［15］中主轴故障树数据为依据进行主轴的模糊Petri网的故障诊断。具体的步骤如下:

(1)将文献［15］中的故障树转化为模糊Petri网模型，如图2所示。

(2)以数控机床主轴切削振动大为例。以切削振动大为主轴故障现象的模糊Petri网模型如图3所示。命题所代表的含义如表1。

(3)建立各个库所的可达性集和立即可达性集，如表2所示。

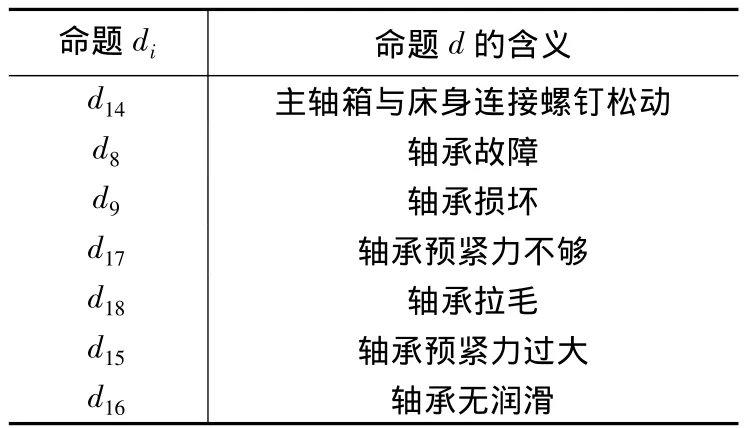
表1 命题di的含义

表2 可达性集和立即可达性集

(4)计算变迁逆向激发值

根据表3模糊取值范围［8］确定变迁的可信度变迁激发的频率，分别为:

根据模糊推理规则，计算求得变迁逆向激发值:

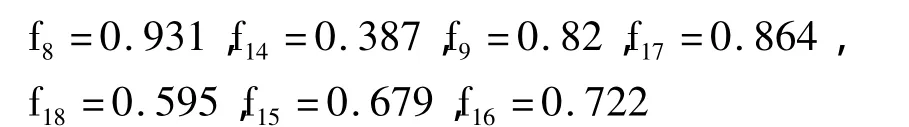
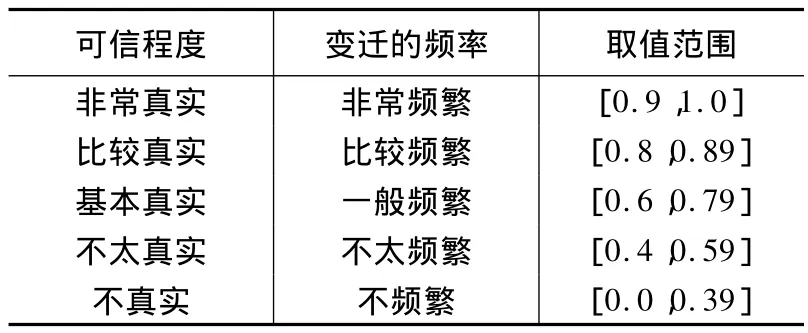
表3 模糊取值范围

(5)逆向推理

根据故障现象主轴切削振动大逆向推理，max(f8，f14)=f8，变迁t8优先逆向激发，输入库所p8为故障部位库所，对应的命题为d8轴承损坏。以库所p8为目标继续逆向推理，max(f8，f17，f18)=f17，变迁 t17优先逆向激发，输入库所p17为故障原因库所，对应的命题为轴承预紧力不够，逆向推理结束。

根据逆向推理，故障现象主轴切削振动大的故障诊断原因顺序依次为:β(p17)=d17，轴承预紧力不够→β(p16)=d16，轴承无润滑→β(p15)=d15，轴承预紧力过大→β(p18)=d18，轴承拉毛→β(p14)=d14，主轴箱与床身连接螺钉松动。

(6)正向激发

逆向推理得到主轴切削振动大的原因为轴承预紧力不够，工作人员检查轴承是否预紧力不够，进行预紧。根据实际情况给予故障原因库所可信度。设定变迁激发的阈值λ=0.73。如果命题“预紧力不够”、“非常真实”，如表3所示，给予库所p17可信度α(17)=0.95＞λ，变迁 t17激发，α18=α17×μ17=0.95×0.96=0.912＞λ，变迁t8激发，最终达到故障现象库所，即故障原因找到。如果命题“预紧力不够”、“不太真实”，如表3所示，给予库所可信度α(17)=0.48＜λ，变迁t17无法激发，说明预紧力不够不是切削振动大的根本原因。再开始检查故障原因轴承无润滑，依次进行故障诊断，直到找到故障原因。

4 结语

本文在传统故障诊断FPN基础上，引入变迁逆向激发值的概念，有助于更加迅速地进行故障诊断，及时排除故障，提高数控机床主轴的可用性。基于改进的模糊Petri网理论对数控机床主轴进行故障诊断的模糊推理，既有定性分析，又有定量分析，计算与图形相结合，逻辑清晰，为今后在计算机上实现打下良好的基础。与此同时，FPN还可以根据实际情况及时进行增减必要的主轴故障原因，以使数控机床主轴的故障信息不断地得到完善。

［1］于捷，贾亚洲.数控车床故障模式影响与致命性分析［J］.哈尔滨工业大学学报，2005(12):1725－1727.

［2］蒋仁言，左明健.可靠性模型与应用［M］.北京:机械工业出版社，1992.

［3］LAN Jinchuan，MA Min.Fault diagnosis method of power system based on the adaptive fuzzy petri net:IEEE Circuits and System International Conference on Testing and Diagnosis，APR28 －29，2009:75 －78［C］.Chengdu:UESTC.

［4］LU Qiuqin，HUANG Guangqiu.Fuzzy analysis of accidents diagnosis based on fuzzy petri net［J］.International Journal of Systems and Control，2007，2(3):228 －236.

［5］袁崇义.Petri网原理［M］.北京:电子工业出版社，1998:25－35.

［6］YUAN Jie，SHI Haibo，LIU Chang，et al.Backward concurrent reasoning based on fuzzy petri nets［C］.2008 IEEE World Congress on Computational Intelligence:Fuzzy Systems(WCCI－ FUZZ2008)，Hongkong，June 2008:832－837.

［7］BINH PTT，TUYEN ND.Fault diagnosis of power system using Neural Petri Net and fuzzy Neural Petri Net［C］.IEEE Power India Conference 2006，ARP 10 －20，2006 New Delhi India.2006 IEEE Power India Conference，2006，1:176 －180.

［8］向永生，刘武，乐晓波，等.基于模糊Petri网的汽车故障诊断仿真研究［J］.计算机工程与科学，2009，31(3):86 －88.

［9］DING Caihong.Application of Petri net to fault diagnosis in satellite［J］.Journal of Systems Engineering and Electronics，2001，12(2):92 －96.

［10］张海燕，夏飞.基于改进Petri网的船舶电力系统故障诊断［J］.船电技术，2010，30(6):35 －38.

［11］XLI F，LARA R.Adaptive fuzzy Petri net for dynamic knowledge representation［J］.Expert Systems with Application ，2000，19(3):235－241.

［12］ZHANG Peng，ZHAO Shiwei，WANG Yake.The research of aircraft fault diagnosis based on adaptive FPN［C］.2009 Chinese Control and Decision Conference，Northeastern University，China、IEEE Industrial Electronics(IE)Chapter，Singapore、Guilin University of Electronic Technology，China.Proceedings of 2009 Chinese Control and Decision Conference，2009:5252 －5255.

［13］林闯.随机Petri网和系统性能评价［M］.北京:清华大学出版社，2000.

［14］丁军，张志华，周学智.模糊Petri网在指火控系统故障诊断中的应用［J］.情报指挥控制系统与仿真技术，2005，27(3):48 －52.

［15］张英芝，申桂香，薛玉霞，等.数控车床主轴模糊故障树分析［J］.吉林大学学报，2006，36(2):66 －68.