环Fp＋uFp上的广义Reed－Muller码

尹 水， 朱士信

（合肥工业大学 数学学院，安徽 合肥 230009）

环Fp＋uFp上的广义Reed－Muller码

尹 水， 朱士信

（合肥工业大学 数学学院，安徽 合肥 230009）

Reed－Muller码是一类非常重要的代数码，具有很好的代数和组合性质。文章首次将Reed－Muller码的概念引入环Fp＋uFp上，定义了更一般的Reed－Muller码URM（p，r，m），给出了它的迹表示，并研究了它的对偶码以及两者之间的关系。特别地，当p＝2时，得到了一些更好的性质。

Reed－Muller码；Kerdock码；Preparata码；Galois环；迹表示

0 引 言

Reed－Muller码首先是由Muller在1954年提出的，之后Reed在其基础上得到了一种新的分组码，称为Reed－Muller码。它最大的优点是易于解码，因而在通信中具有广泛的应用前景，一直是人们关注的热点。文献［1］中详细介绍了二元Reed－Muller码，根据布尔函数给出了一个简单直观的定义，并研究了它的一些基本性质及应用。

近年来，有限环尤其是有限链环上的代数编码理论引起了许多学者的兴趣［2－6］。随着Z4环上编码理论的研究日趋成熟，人们逐渐探索出一种研究有限链环上的Reed－Muller码的方法［7－9］。文献 ［10］首 次 在 环Fp＋uFp上 引 入Kerdock码和Preparata码的相关概念，给出了该环上 Kerdock码Kp，m和 Preparata码Pp，m的 定义，证明了它们互为对偶码。特别地，当p＝2时，建立了环F2＋uF2上的这2类码与二元r阶Reed－Muller码之间的联系，即它们的剩余码分别为R（1，m）和R（m－2，m），且R（1，m）为环R2上Kerdock码K2，m的线性子码的Gray象。

本文在此基础上进一步加以研究，将Reed－Muller码的概念引入环Fp＋uFp上，给出了更一般的Reed－Muller码URM（p，r，m）的定义，并且研究了一些相关的性质。

1 预备知识

记Rp＝Fp＋uFp，其中p为素数，Fp为有限域，u2＝0，规定其上的加法和乘法为域Fp上的加法和乘法。

令＝｛（x1，x2，…，xn）｜xi∈Rp，i＝1，2，…，n｝。环Rp上一个长为n的p元线性码定义为Rp－模的一个加法子模，简称为Rp－线性码。环Rp上任一非零的Rp－线性码C都等价于矩阵

生成的Rp－线性码，其中A、B1、B2、C为Fp上的矩阵。显然C的类型为，且其码字个数

对于∀x＝（x1，x2，…，xn），y＝（y1，y2，…，yn）∈，定义x和y的内积为x·y＝x1y1＋x2y2＋…＋xnyn。若x·y＝0，则称x与y正交。称C⊥＝｛x∈｜∀y∈C，x·y＝0｝为C的对偶码。对于环Rp上的线性码C，如果对于∀（c0，c1，…，cn－1）∈C，都有（cn－1，c0，c1，…，cn－2）∈C，那么称C为环Rp上的循环码，简称为Rp－循环码。环中的码字（c0，c1，…，cn－1）与Rp［x］／（xn－1）中的多项式c0＋c1x＋…＋cn－1xn－1一一对应，从而环Rp上长为n的循环码与Rp［x］／（xn－1）的理想一一对应，在不引起混淆的情况下，认为这2种表达是一样的。

在环Rp中，任意元素c都可唯一地表示成c＝a＋ub，其中a，b∈Fp。称＝a为c的模u约化。更一般地，称¯h（x）＝的模u约化。若（x）是Fp［x］中的不可约多项式，则称h（x）是Rp［x］中的基本不可约多项式；若（x）是Fp［x］中的m次本原多项式，则称h（x）是Rp［x］中的m次基本本原多项式。称（x）＝xdeg（h（x））h（1／x）为h（x）的互反多项式。对于Rp［x］中首一的m次基本本原多项式h（x），称Rp［x］／（h（x））为环Rp的 Galois扩环，记为GR（Rp，m）。GR（Rp，m）中的任一元素γ都可以唯一表示成γ＝α＋uβ，其中α，β∈Fpm。

本文仍然沿用文献［10］中关于迹映射的记号，定义Galois环GR（Rp，m）上的Frobenius映射为：

易证f是环GR（Rp，m）上的环自同构，f的固定元素恰好全为环Rp中的元素，并且f的阶为m。定义从环GR（Rp，m）到环Rp的迹映射为：

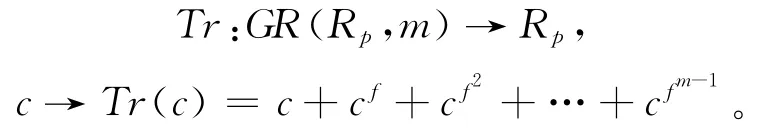
显然Tr是线性的，且为满射。

2 环Fp＋uFp上的Reed－Muller码

2.1 相关定义与命题

令m为一个大于等于2的整数，n＝pm－1。设h（x）为多项式环Rp［x］中首一的m次基本本原多项式，且h（x）｜（－1），那么在 Galois环GR（Rp，m）＝Rp［x］／（h（x））中存在h（x）的一个根ζ，并且ζ的阶为pm－1，h（x）的m个不同的根为ζ，ζp，…。对于（m＋1）×pm阶矩阵

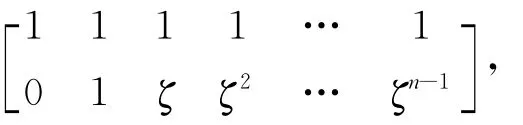
将它的列依序标号为∞，0，1，2，…，n－1，如果ζj＝c1j＋c2jζ＋…＋cmjζm－1（j＝∞，0，1，…，n－1），其中cij∈Rp（i＝1，2，…，m），这里约定ζ∞＝0，那么用（c1j，c2j，…，cmj）′替代ζj，将它的行依序标号为0，1，2，…，m。记该矩阵的第i个行向量为xi，那么xi（i＝0，1，2，…，m）为环Rp上的pm－元组，其中x0为全1的pm－元组。简便起见，定义2个向量之间的分量积为：（a∞，a0，a1，…，an－1）（b∞，b0，b1，…，bn－1）＝ （a∞b∞，a0b0，a1b1，…，an－1bn－1）。

定义1 设整数m≥2，n＝pm－1，0≤r≤m，那么在环Rp上由所有形如…（1≤i1＜i2＜…＜is≤m，0≤s≤r）的pm－元组生成的Rp－线性码，称为环Rp上的r阶 Reed－Muller码，记为URM（p，r，m）。这里约定：当s＝0时，有

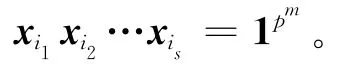
根据定义1，立即可以得到命题1～命题4。

命题1 对于任意整数0≤r≤m，URM（p，r，m）的类型为，其中

命题2 环Rp上的1阶Reed－Muller码为环Rp上的 Kerdock码，即 URM（p，1，m）＝Kp，m。

证明 当r＝1时，由定义1及文献［10］中定义1可知，URM（p，1，m）的生成矩阵即为Kp，m的生成矩阵，得证。

当p＝2时，环R2上的r阶Reed－Muller码URM（2，r，m）有一些很好的性质。

命题3 环R2上的2m个2m－元组…（1≤i1＜i2＜…＜is≤m，0≤s≤m），构成了自由R2－模的一组基。

证明 证明与文献［8］中引理10.3类似。

记 URM（p，r，m）的剩余码为：

那么有命题4。

命题4 URM（2，r，m）的剩余码等价于二元r阶 Reed－Muller码R（r，m），即＝R（r，m）。

证明 由定义1可知，当p＝2时，对于任意的c＝a＋ub∈URM（2，r，m），都存在∈R2（1≤i1＜i2＜…＜is≤m，0≤s≤r），使得：

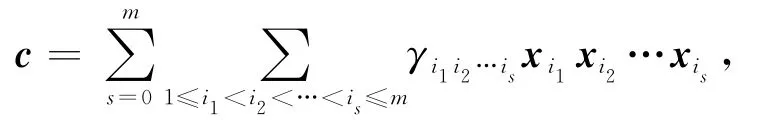
那么，c的模u约化为：

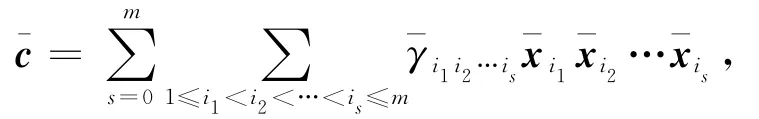
这里的∈F2。显然，a＝∈，由c的任意性可知，是由所有形如…（1≤i1＜i2＜…＜is≤m，0≤s≤r）的2m－元组生成的。不难证明，如果写成矩阵形式，那么与二元r阶Reed－Muller码R（r，m）的生成矩阵是等价的，所以＝R（r，m）。

证毕。

2.2 定理1及其证明

文献［10］的重要结果之一是给出了环Rp上Kerdock码Kp，m和 Preparata码Pp，m的 迹 表 示，自然地，本文也将给出环Rp上的r阶Reed－Muller码 URM（p，r，m）的迹表示。

在这里，引入p－重量的概念。令正整数j的p进制展开为j＝，其中λi∈Fp且λt≠0。称λ0，λ1，λ2，…，λt之中非零项的个数为j的p－重量，记为ωp（j），即

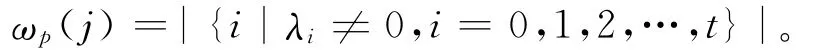
另外，定义0的p－重量ωp（0）＝0。特别地，如果正整数j的p进制展开式的系数满足λ0，λ1，λ2，…，λt－1＝0或1，且λt＝1，那么就将j记为j（2），称它的p－重量为二元p－重量，记为（j），显然（j）＝。同样地，定义0的二元p－重量（0）＝0。

设正整数m为某一固定的值，令整数r和s满足0≤r，s≤pm－2。如果存在非负整数i，使得pir≡s（modpm－1），则r与s等价。显然，这定义了整数集｛0，1，2，…，pm－2｝上的一个等价关系，称这些等价类为模pm－1的分圆陪集。容易看出，如果r和s属于同一个分圆陪集，那么就有ωp（r）＝ωp（s）。特别地，如果r可记为r（2），且和s属于同一个分圆陪集，那么s也可记为s（2），且有（r）＝（s）。称分圆陪集中取值最小的一个数为该分圆陪集的代表元。

令Γ＝｛0，1，2，…，pm－2｝，Γ（2）表示Γ中可记为j（2）的元素的集合，则有定理1。

定理1 设整数m≥2，n＝pm－1，那么URM（p，0，m）是长为pm的Rp－重复码｛｜a∈Rp｝，且当1≤r≤m时，URM（p，r，m）是由URM（p，0，m）以及所有形如

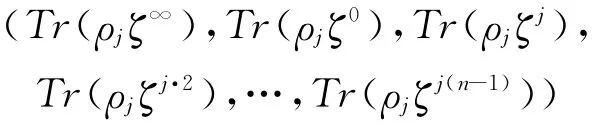
的pm－元组生成的，其中j∈Γ（2）取遍模pm－1的分圆陪集中满足（j）≤r的陪集的代表元集，而ρj取遍Galois环GR（Rp，m）。

证明 由定义1知，

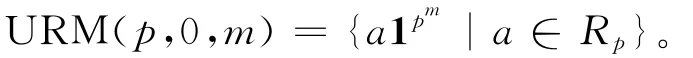
现令1≤r≤m，将题设中由URM（p，0，m）以及所有形如

的pm－元组生成的Rp－线性码，记为Cp，r。

当r＝1时，由命题2，URM（p，1，m）＝Kp，m，再由文献［10］中的定理1可知：

因此 URM（p，1，m）＝Cp，1。由定义1，URM（p，1，m）是由，x1，x2，…，xm生成的，对于每一个xi（i＝1，2，…，m），都存在唯一的σi∈GR（Rp，m），使得：

下证当r＝2时的情形，需证 URM（p，2，m）＝Cp，2。

由定义1可得：

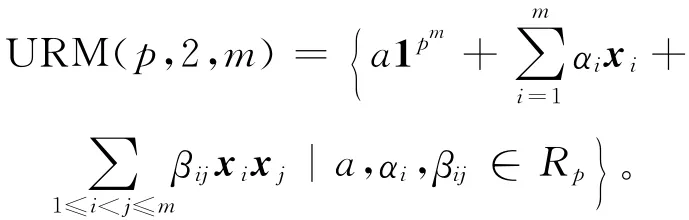
当r＝1时，有 URM（p，1，m）＝Cp，1⊆Cp，2，因此＋∈Cp，2。

易知：

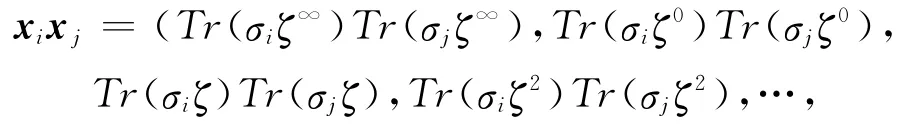
对于k∈｛∞，0，1，2，…，n－1｝，由迹映射的定义可得：

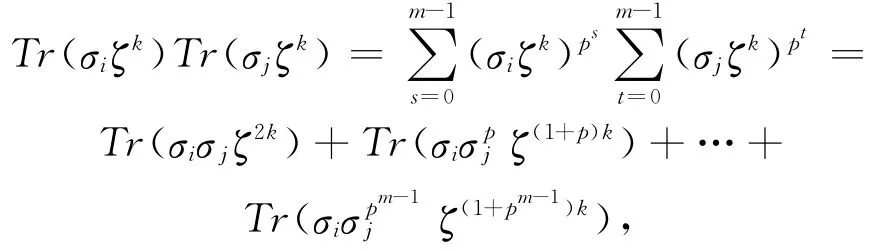
则可将xixj写成如下形式：

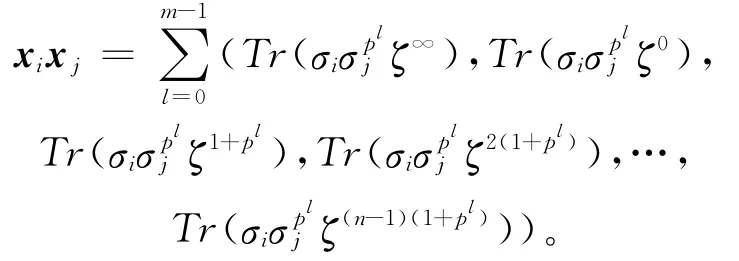
显然，当l＝0时，（2）＝1，则

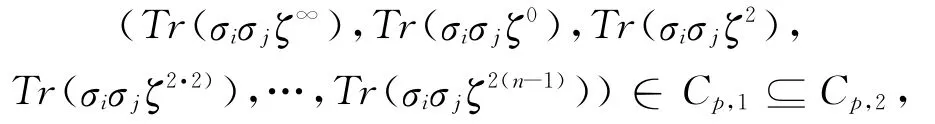
而当1≤l≤m－1时（1＋pl）＝2，则

从而xixj∈Cp，2（1≤i＜j≤m），因此 URM（p，2，m）⊆Cp，2。

另一方面，将删去Cp，2中码字第∞位置分量所得的删减码记为。那么，显然是由以及所有形如

（Tr（ρjζ0），Tr（ρjζj），Tr（ρjζj·2），…，Tr（ρjζj（n－1）））的（pm－1）－元组生成的Rp－线性码，其中j∈Γ（2）取遍模pm－1的分圆陪集中满足（j）≤2的陪集的代表元集，而ρj取遍Galois环GR（Rp，m）。类似于文献［10］中的定理1，容易验证，中所有元素对应的多项式都能被多项式（x）零化，其中，而（x）是多项式h2（x）的的互反多项式，则有：

令g2（x）为多项式

的互反多项式，即

记环Rp上由g2（x）生成的循环码为C。那么，（x）即为C的校验多项式，故有Cp，2⊆C，从而URM（p，2，m）⊆Cp，2⊆C。易证：

又根据命题1可知，当r＝2时，URM（p，2，m）的类型为 （，所 以 有｜URM （p，2，m）｜＝（＝ （p2＝｜C｜。 综 上 可 得，URM（p，2，m）＝Cp，2＝C。

对于r≥3时的情形，可以同上类似地证明。

证毕。

事实上，定理1是环Rp上的r阶Reed－Muller码URM（p，r，m）（0≤r≤m）的一个等价定义，给出了其中元素的迹表示。由上述定理的证明，立即可以得到下列推论。

推论1 记环Rp上删去URM（p，r，m）中码字第∞位置分量所得的删减码为URM（p，r，m）－，那么 URM（p，r，m）－为Rp－循环码，其生成多项式为：

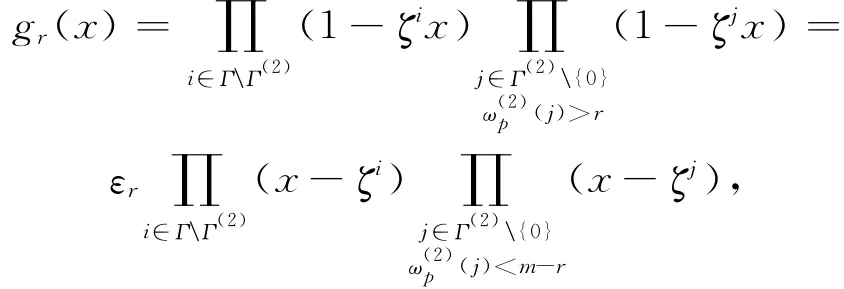
其中，εr＝±1。

推论2 设整数m≥2，那么对于任意的c＝（c∞，c0，c1，…，cn－1）∈URM（p，r，m），当p≥3时，在环Rp上，对于任意整数0≤r≤m，都有：

而当p＝2时，在环R2上，（1）式对于0≤r≤m－1成立。

证明 只需证明定理1中给出的URM（p，r，m）的所有生成元都满足（1）式即可。首先，m≥2，对于，在环Rp上有：

其次，对于 URM（p，r，m）的所有生成pm－元组，则有：

其中，（2）式的最后一步是因为ζn＝＝1，若p≥3，则对于任意0≤r≤m，j∈Γ（2），（j）≤r≤m，都有≠1；而若p＝2，则对于0≤r≤m－1，（j）≤r≤m－1，有≠1。证毕。

注意，对于推论2，当p＝2，r＝m时，如果（j）＝m，那么j＝1·20＋1·21＋…＋1·2m－1＝2m－1，此时分式的分母为1－＝1－＝1－1＝0。

2.3 定理2及其证明

定理2 设整数m≥2，n＝pm－1，0≤r≤m－1，则有URM（p，m－r－1，m）⊆URM（p，r，m）⊥。

证明 首先，证明全1的pm－元组∈URM（p，m－r－1，m）属于 URM（p，r，m）⊥。显然，·＝0。此外，还需证明与定理1中给出的 URM（p，r，m）的所有生成pm－元组都正交。由推论2可知＝0，其中j∈Γ（2），（j）≤r。因此，1pm∈URM（p，r，m）⊥。

下面证明任意的c＝（c∞，c0，c1，…，cn－1）∈URM（p，m－r－1，m）都属于 URM（p，r，m）⊥。由前面的约定ζ∞＝0，则有Tr（ρjζ∞）＝Tr（0）＝0，从而易证：

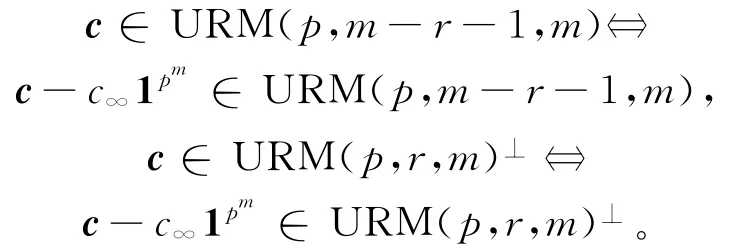
因此，只需证明 URM（p，m－r－1，m）中任意满足c∞＝0的c都属于 URM（p，r，m）⊥即可。令c＝（0c＇），其中c＇＝（c0，c1，…，cn－1），显然c＇∈URM （p，m－r－1，m）－。 由 推 论 1，URM（p，m－r－1，m）－为Rp－循环码，其生成多项式为：

其中εm－r－1＝±1。所以，gm－r－1（x）｜c（x），其中c（x）＝c0＋c1x＋…＋cn－1xn－1。

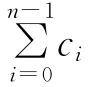
则c（x）fm－r－1（x）＝0。因此，c（x）属于以多项式（x）为生成多项式的Rp－循环码的对偶码，且有：

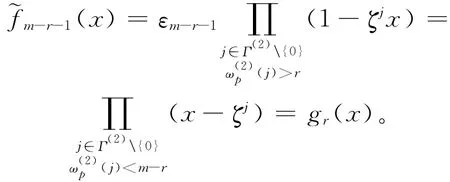
根据推论1，以gr（x）为生成多项式的Rp－循环码是 URM（p，r，m）－，因而c（x）∈（URM（p，r，m）－）⊥。由于c∞＝0，因此c∈URM（p，r，m）⊥。故有：

证毕。

特别地，当p＝2时，有以下结论。

推论3 设整数m≥2，n＝2m－1，0≤r≤m－1，则有 URM（2，m－r－1，m）＝URM（2，r，m）⊥。

证明 由定理2可得，URM（2，m－r－1，m）⊆URM（2，r，m）⊥。

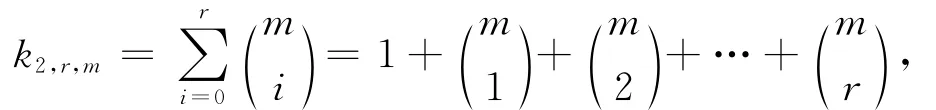
显然 URM（2，r，m）⊥与 URM（2，m－r－1，m）类型一致，所以 URM（2，m－r－1，m）＝URM（2，r，m）⊥。

推论4 URM（p，m－2，m）⊆Pp，m，特别地，有 URM（2，m－2，m）＝P2，m。

证明 由定理2、命题2及文献［10］中定理2可得：

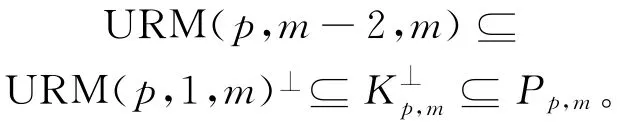
特别地，当p＝2时，由推论3有：

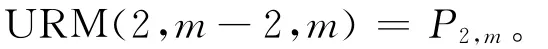
3 结束语

有限环上的Reed－Muller码不仅在理论上可以用来构造一些很好的码，如Kerdock码、Preparata码以及Goethals码等，而且在实际中也有着广泛的应用，因而具有很大的研究价值。本文将Reed－Muller码的概念引入环Fp＋uFp上，给出了更一般的Reed－Muller码 URM（p，r，m）的定义，用一个等价定义给出了其中元素的迹表示，并且研究了其他的一些相关性质。至于更一般的有限环上的Reed－Muller码，还有待于进一步加以研究。

［1］Macwilliams F J，Sloane N J A.The theory of error－correcting codes［M］.Amsterdam：North Holland Publishing Co，1977：370－479.

［2］Bonnecaze A，Udaya P.Cyclic codes and self－dual codes overF2＋uF2［J］.IEEE Trans Inform Theroy，1999，45（4）：1250－1255.

［3］Gaborit P.Mass formulas for self－dual codes overZ4andFq＋uFqrings［J］.IEEE Trans Inform Theroy，1996，42（4）：1222－1228.

［4］Qian Jianfa，Zhang Lina，Zhu Shixin.Cyclic codes overFp＋uFp＋…＋uk－1Fp［J］.IEICE Trans Fundamentals，2005，E88－A：795－797.

［5］李富林，朱士信.环Fp＋uFp＋…＋ukFp上的准循环码［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2009，32（11）：1766－1768.

［6］汤道安，朱士信，唐永生.环F2＋uF2＋…＋ukF2上的自对偶码［J］.合肥工业大学学报：自然科学版，2010，33（3）：478－480.

［7］Hammons A R，Kumar P V，Calderbank A R，et al.TheZ4－linearity of Kerdock，Preparata，Goethals，and related codes［J］.IEEE Trans Inform Theroy，1994，40（3）：301－319.

［8］Wan Zhexian.Quaternary codes［M］.Singapore：World Scientific，1997：113－176.

［9］Bhaintwal M，Wasan S K.Generalized Reed－Muller codes overZq［J］.Designs Codes Cryptogr，2010，54（2）：149－166.

［10］吴 波，朱士信，李 平.环Fp＋uFp上的Kerdock码和Preparata码［J］.电子学报，2008，36（7）：1364－1367.

Generalized Reed－Muller codes over the ringFp＋uFp

YIN Shui， ZHU Shi－xin
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

Reed－Muller codes form a very important family of algebraic codes that have very nice algebraic and combinatorial properties.In this paper，the concept of the Reed－Muller code is first introduced into the ringFp＋uFp，which is denoted by URM（p，r，m）.Its trace representation is given，and its dual code and the relationship between them are studied.Especially，some better properties are obtained whenp＝2.

Reed－Muller code；Kerdock code；Preparata code；Galois ring；trace representation

O157.4

A

1003－5060（2012）04－0571－06

10.3969／j.issn.1003－5060.2012.04.031

2011－07－25；

2011－09－16

尹 水（1987－），男，安徽宿松人，合肥工业大学硕士生；

朱士信（1962－），男，安徽枞阳人，博士，合肥工业大学教授，博士生导师.

（责任编辑 张淑艳）