蠕变载荷下有机玻璃银纹萌生及损伤研究

吴国夫， 朱西平， 高宗战， 岳珠峰

（西北工业大学力学与土木建筑学院，西安 710072）

国产MDYB-3有机玻璃是目前国内首选的座舱盖透明材料，在其使用过程中受到载荷、温度、环境等多种因素共同作用造成的蠕变损伤。银纹化现象作为有机玻璃等高聚物特有的一种现象，伴随在有机玻璃断裂失效的整个过程中，是沟通有机玻璃宏观失效和微观机理的桥梁。这样，深入了解银纹的萌发机理及银纹损伤规律就具有重要的理论意义和应用价值，也是实现有机玻璃断裂失效表征的有效途径［1～6］。

关于银纹的萌生机制，国内外学者提出了许多判据，如最大主应力判据、临界应变判据、主应力差判据、等效剪切应力判据等，这些判据主要集中在材料的局部应力和应变方面［7］。Bucknall回顾了高聚物银纹萌生判据的优缺点，基于线弹性断裂力学，提出了新的银纹萌生判据［8］。Estevez R等模拟了玻璃态高聚物银纹和剪切屈服的主导因素，对玻璃态聚合物的银纹化过程进行了数值模拟分析［9］。Saad-Gouider校准了Estevez R给出模型的参数，提出了粘塑性区域在连续变形时同时考虑屈服软化和硬化的粘弹性本构关系［10］。罗文波对有机玻璃试样进行了拉伸蠕变实验，采用光学技术定量研究了银纹损伤为主的蠕变损伤，给出了银纹萌生的时间-应力包络线，并通过理论分析，得到了银纹损伤演化方程［11，12］。Jie等提出了带状银纹模型，通过对实验数据进行拟合，得到银纹应力与裂纹扩展速率的关系［13］。贾敬华等通过实验得到了MDYB-3有机玻璃等幅疲劳扩展规律和疲劳裂纹扩展门槛值［14］。高宗战等实验观测和分析了不同应力和不同温度下PMMA的蠕变损伤过程［15］。

迄今为止，尽管已有蠕变载荷作用下对有机玻璃银纹损伤开展的研究，给出了有机玻璃银纹损伤密度随应力和时间的演化规律，但对蠕变载荷作用下有机玻璃银纹萌生时间准则的研究却鲜有报道。然而银纹萌生时间具有明显的应力相关性，并且多数情况下更关心银纹何时萌生，因此对银纹萌生时间准则的研究具有重要意义。另外银纹损伤密度作为衡量银纹萌生、扩展的重要标准，要更好地了解有机玻璃银纹损伤密度随时间和应力的演化规律，就必须建立银纹损伤密度的增长模型，现有的银纹损伤密度的增长模型很多，但是大多只能部分描述银纹萌生或银纹扩展的初始阶段。

本研究对MDYB-3航空有机玻璃开展了常温蠕变实验，研究了在蠕变载荷作用下有机玻璃银纹萌生、扩展及蠕变失效过程。基于实验数据和图像处理与分析，提出了银纹萌生的应力-时间准则;通过研究银纹损伤密度变化，建立了MDYB-3有机玻璃蠕变载荷下银纹损伤随时间和应力的演化规律。

1 实验装置和方法

1.1 实验装置

实验系统由三部分组成:（1）根据杠杆原理设计的一套简单、实用、稳定的蠕变加载系统（如图1），可进行长时间的蠕变实验。为使杠杆系统只对试样产生轴向拉伸作用，在杠杆两侧加设固定装置，以防止杠杆对试样存在弯扭作用;（2）银纹损伤图像采集系统，由Dino-lite光学显微镜、摄像头和计算机组成;（3）IPP 6.0图像分析系统，用以测量试样的银纹损伤密度。

图1 蠕变加载系统Fig.1 Loading system under creep

1.2 实验方法

实验材料选用与飞机座舱盖有机玻璃相同制造工艺、相同厚度（18mm）的MDYB-3有机玻璃板材，采用数控机床进行试样加工，以前采用此种方法加工过有机玻璃疲劳试样，加工精度可靠。试样的形状参考ASTM标准、国家实验标准及航空标准，采用“双犬骨”形试样（如图2）。对每件试样的加工质量进行检测，确保实验前试样表面均未损伤。对试样进行常温（21.5±0.5℃）下的拉伸蠕变实验，分别在三种应力水平（48.1MPa、51.8MPa、55.5MPa）下用杠杆加载系统稳定加载直至试样蠕变断裂失效。

图2 有机玻璃试样Fig.2 Specimen of PMMA

实验过程中不取下试样，使用Dino-lite高倍显微镜在试样相同位置实时观测并进行图像采集。在实验刚开始、银纹萌生后，银纹扩展得比较快，采集图像的时间间隔较短;随着实验的继续，银纹扩展的速度放缓，此时图像采集的时间间隔也可适当变长。

将采集到的数据存于电脑中，应用IPP 6.0图像分析系统进行图像分析，计算图像中银纹损伤面积与视场总面积之比，即为有机玻璃试样在该应力、时间和放大倍数下的银纹损伤密度。

2 实验结果与分析

2.1 实验结果

分别在各组有机玻璃试样上选取三个区域进行分析（如图3），将这三个区域图像银纹损伤密度的平均值作为有机玻璃试样在该时间、应力水平下的银纹损伤密度。

图3 编号752、载荷55.5MPa、加载29小时时选取的三个区域图像Fig.3 Three pictures from group752 loaded for 29 hours under the stress of 55.5 MPa

实验中选用光学显微镜放大，发现有机玻璃银纹（沿垂直于载荷方向）呈现稀疏→稠密→稀疏→稠密→稀疏的特征（如图4）。

2.2 有机玻璃在常温下银纹萌生的时间准则

图4 银纹特征 （a）编号651、载荷48.1MPa、加载252小时;（b）编号701、载荷51.8MPa、加载84小时;（c）编号751、载荷55.5MPa、加载26小时Fig.4 Character of craze （a）specimen from group651 loaded for 252 hours under the stress of 48.1 MPa;（b）specimen from group701 loaded for 84 hours under the stress of 51.8 MPa;（c）specimen from group751 loaded for 26 hours under the stress of 55.5 MPa

表1 银纹萌生时间实验记录与曲线分析结果Table 1 The time of crazing initiation from experiment recording and curve analyzing

由表1对比分析实验记录结果和曲线拟合结果可以得到对应于不用应力下的银纹萌生时间t0（σ）。

将银纹萌生时间对应力进行非线性回归分析，得到银纹萌生时间与应力关系（如图5），经拟合得到相关系数R=1的常温下银纹萌生时间准则:

图5 银纹萌生时间曲线Fig.5 The time curve of crazing initiation

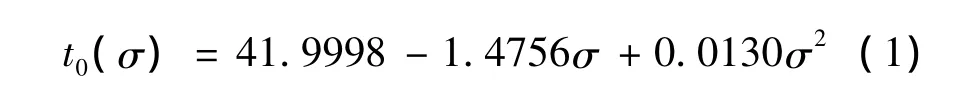
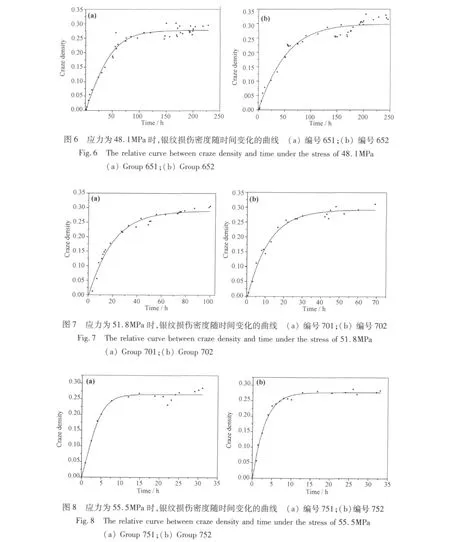
常温下对于银纹萌生存在临界应力σf，当材料所受应力超过σf时，材料在不经过任何塑性变形的情况下突然失效，此时银纹还未萌生，材料已经失效，所以对应的银纹萌生时间趋于零。

由实验拟合结果可知σf=56.7538MPa，因此式（1）适用于σ≤σf=56.7538MPa的情况。

不同应力水平下，银纹萌生时间不同。随着应力水平的提高，银纹萌生时间非线性缩短。

2.3 有机玻璃在常温下银纹损伤密度的增长模型

2.3.1 有机玻璃常温下银纹损伤密度变化规律 图6到图8分别给出了在常温下应力分别为48.1MPa、51.8MPa、55.5MPa时MDYB-3有机玻璃银纹损伤密度随时间变化的曲线。可见有机玻璃银纹损伤密度随着时间的推移逐渐增加，时间越长，有机玻璃的损伤程度越严重，银纹损伤表现出明显的时间相关性。

在银纹扩展的初始阶段，银纹损伤密度增长很快，基本呈线性增长，这一阶段为银纹快速扩展阶段，大概占有机玻璃蠕变断裂失效寿命的1/3时间，此时没有宏观裂纹存在。由此阶段银纹损伤密度随时间变化曲线的斜率发现:应力水平越高，银纹损伤密度的增长越快，表现出银纹损伤明显的应力相关性。

银纹快速扩展阶段之后的很长一段时间内，银纹损伤密度增长缓慢，尤其是在有机玻璃断裂失效前，银纹损伤密度变化不大，这一阶段为银纹缓慢扩展阶段，此时已经有明显的宏观裂纹存在，这个阶段占有机玻璃蠕变断裂失效寿命的2/3时间，是银纹快速扩展阶段持续时间的两倍。

有机玻璃在蠕变断裂失效前银纹损伤密度增长缓慢，虽然不同应力水平下有机玻璃蠕变断裂失效时间不同，但是其在断裂失效时的银纹损伤密度集中在30%左右，可以由此来表征MDYB-3有机玻璃在常温下的蠕变断裂失效。实际操作中可以通过对使用MDYB-3有机玻璃的舱盖进行银纹损伤密度测量分析，就能提前预测舱盖失效的大致时间，避免事故的发生。

2.3.2 有机玻璃常温下银纹损伤密度增长模型由于常温下，MDYB-3有机玻璃银纹损伤密度具有明显的时间与应力相关性（如图6到图8），可以假设MDYB-3有机玻璃银纹损伤密度满足:

其中D（σ，t）为银纹损伤密度，A（σ），B（σ）为与应力有关的材料参数，其值由实验数据确定，t为时间;公式适应于t＞t0（σ），t0（σ）是银纹萌生的时间，由式（1）确定，也与应力有关。

依式（1）对各组实验数据进行双曲线函数非线性拟合，分别得到一组系数A（σ）和B（σ）与应力的关系（如图9和图10）。

图9 A（σ）-σ变化曲线Fig.9 The relative curve between A（σ）and σ

经拟合，相关系数R=1，两者相关性最高，所得二次多项式分别为:

图10 B（σ）-σ变化曲线Fig.10 The relative curve between B（σ）and σ

最后将式（1）、（3）、（4）代入式（2），得到 MDYB-3有机玻璃银纹损伤密度随时间和应力的增长模型为:

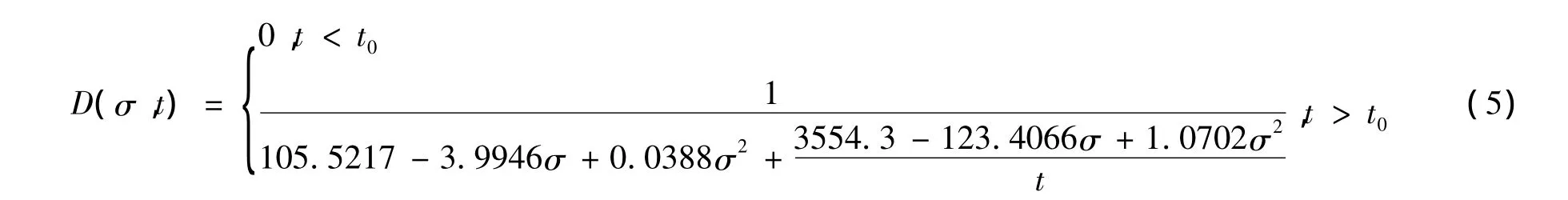
其中t0（σ）=41.9998-1.4756σ+0.0130σ2，得到了有机玻璃常温蠕变条件下银纹损伤密度随时间和应力的演化规律。

为验证式（5）的适用性，特在常温下增加两组验证性实验，所施加载荷为50.0MPa和53.6MPa，得到两组实验数据，分别与拟合得到的银纹损伤密度增长模型结果进行对比（如表2）。

表2 应力分别为50.0MPa和53.6MPa时，银纹损伤密度随时间的变化Table 2 The relationship between craze density and time under the stress of 50.0MPa and 53.6MPa

结果表明模型预测的结果与验证实验的结果非常接近，由此可以证明所提出的关于MDYB-3有机玻璃常温蠕变条件下银纹损伤密度随时间和应力的增长模型具有较广泛的适用性。

3 结论

（1）通过对MDYB-3有机玻璃开展的常温蠕变实验，在研究其银纹萌生、扩展及断裂失效过程中发现，有机玻璃银纹（沿垂直于载荷方向）的排列特征为:稀疏→稠密→稀疏→稠密→稀疏。

（2）基于实验数据，以银纹损伤密度为变量，提出了有机玻璃不同应力水平下银纹萌生的时间准则;发现常温下随着应力的提高，有机玻璃银纹萌生时间非线性缩短;而且银纹萌生存在临界应力σf，当材料所受应力超过σf时，材料在不经过任何塑性变形的情况下突然失效，此时银纹还未萌生，材料已经失效，所以对应的银纹萌生时间趋于零。

（3）通过研究银纹损伤密度变化，建立了有机玻璃银纹损伤密度的增长模型，验证发现用双曲线函数可以对银纹损伤密度变化进行很好的描述，由此得到了有机玻璃常温蠕变条件下银纹损伤密度随时间和应力的演化规律。

［1］罗文波，杨挺青，张平.高聚物细观损伤演化的研究进展［J］.力学进展，2001，31（2）:264-275.

（LUO W B，YANG T Q，ZHANG P.An extensive review on meso-damage evolution in polymers ［J］.Advances in Mechanics，2001，31（2）:264-275.）

［2］范金娟，张卫方，陈新文.定向有机玻璃的拉伸断裂行为研究［J］.航空材料学报，2006，26（5）:106-108.

（FAN J J，ZHANG W F，CHEN X W.Investigation of tensile facture behavior of directional PMMA［J］.Journal of Aeronautical Materials，2006，26（5）:106-108.）

［3］颜志军，罗文波，张平.高聚物银纹损伤与断裂的研究现状［J］.高分子材料科学与工程，2002，18（4）:41-44.

（YAN Z Z，LUO W B，ZHANG P.Current situation on the studies of craze fracture in polymers［J］.Polymer Materials Science and Engineering，2002，18（4）:41-44.）

［4］熊芬，管蓉，鲁德平，等.聚合物银纹研究进展［J］.高分子通报，2006，1:44-52.

（XIONG F，GUAN R，LU D P，et al.Polymer craze and its progress［J］.1 ，2006，1:44-52.）

［5］郭伟国，史飞飞.不同载荷方式下MDYB-3有机玻璃变形与破坏行为［J］.航空学报，2008，29（6）:1517-1525.

（GUO W G，SHI F F.Deformation and failure behavior of MDYB-3 oriented PMMA glass under different loading conditions［J］.ACTA AeroNautica ET Astronautica Sinica，2008，29（6）:1517-1525.）

［6］姚卫星.飞机结构疲劳寿命分析的一些特殊问题［J］.南京航空航天大学学报，2008，40（4）:433-441.

（YAO W X.Some special subject of fatigue Life prediction on aircraft structures［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2008，40（4）:433-441.）

［7］ MARISSEN R.Craze growth mechanics ［J］.Polymers，2000，41:1119-1129.

［8］BUCKNALL C B.New criterion for craze initiation［J］.Polymer，2007，48:1030-1041.

［9］ESTEVEZ R，Tijssens MGA，Van der Gisessen E.Modeling of the competition between shear yielding and crazing in glassy polymers［J］.J Mech Phys Solids，2000，48（2）:585-617.

［10］SAAD-GOUIDER N，ESTEVEZ R，C OLAGNON，et al.Calibration of a viscoplastic cohesive zone for crazing in PMMA［J］.Engineering Fracture Mechanic，2006，73:2503-2522.

［11］罗文波，刘文娴，杨挺青，等.一种高聚物银纹损伤演化的实验研究［J］.固体力学学报，2004，25（2）:171-175.

（LUO W B，LIU W X，YANG T Q，et al.Experimental study on crazing damage in polymers［J］.ACTA Mechanica Solida Sinica，2004，25（2）:171-175.）

［12］LUO Wenbo，LIU Wenxian.Incubation time to crazing in stressed poly［J］.Polymer Testing，2007，26:413-418.

［13］M.Jie，C.Y.Tang.Limitation on crack speed for a stripcraze model applied to PMMA ［J］.Theoretical and Applied Fracture Mechanics，2000，34:11-16.

［14］贾敬华，李亚智，肖健.YB-MD-3有机玻璃的疲劳裂纹扩展特性研究［J］.航空材料学报，2006，26（5）:109-112.

（JIA J H，LI Y Z，XIAO J.Study of fatigue crack propagation behavior of YB-MD-3 PMMA plates［J］，Journal of Aeronautical Materials，2006，26（5）:109-112.）

［15］GAO Zongzhan，GOU Xingwang，YUE Zhufeng.The Creep Behavior Analysis of PMMA with different stress and under different Temperature［J］.FM2009:261-264.