伽尔顿板实验小球分布的研究

晋宏营 刘美云

（榆林学院能源工程学院，陕西 榆林 719000）

1 引言

伽尔顿板实验可以形象地说明大数目随机事件中的统计规律，以及统计规律中伴随的涨落现象.伽尔顿板装置是在一块竖直木板的上部规则地钉上许多钉子，木板的下部用竖直隔板隔成许多等宽的狭槽，从板顶漏斗形的入口处可以投入小球，板前覆盖玻璃，以使小球留在狭槽内［1］.实验表明：当从入口处投入一个小球时，小球最后落入哪个狭槽是偶然的；当投入大量小球时，可看到最后落入各狭槽的小球数目不相同，在中央的槽内小球数目最多，离中央越远的槽内小球越少；当小球数目较多时，重复该实验，每次得到的小球分布彼此近似地重合［1，2］.伽尔顿板实验中大量小球的分布服从一定的统计规律，近似于正态分布，但由于伽尔顿板左右侧面的阻挡限制，该分布的范围与正态分布有差别，不是从-∞到＋∞.伽尔顿板实验中小球分布的函数解析式是什么，教材和其他文献中没有给出［1～5］.我们使用最大熵原理研究了伽尔顿板实验中小球的分布，得到了小球分布的概率密度函数解析表达式；我们还在计算机上对该实验进行了蒙特卡罗模拟，并把模拟得到的小球分布与导出的小球理论分布进行了比较.

2 伽尔顿板实验中小球理论分布的推导

最大熵原理是统计物理中的一个基本原理，它指出：一个宏观系统的信息熵（广义熵）在一组约束条件下趋于约束极大值.按照此原理，对于一个宏观系统，如果我们选择合适的约束条件，利用拉格朗日乘子法等方法计算其信息熵的约束极大值，原则上可以求出该系统的分布［6］.作为自然界的一个基本规律，最大熵原理已在很多领域得到广泛应用［6～8］，下面我们使用最大熵原理对伽尔顿板实验中小球分布的具体表达式进行推导.

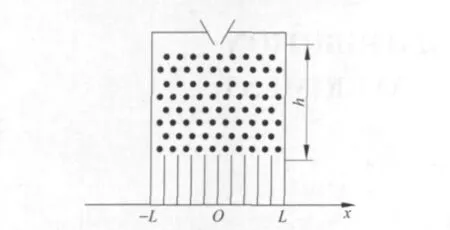
图1 伽尔顿板实验装置

伽尔顿板实验装置如图1所示，图中黑点代表钉子，下面是狭槽.设入口处相对于狭槽的高度为h，以板底中心为坐标原点，沿板底为x轴建立坐标系，见图1，原点到板底两端的距离均为L.设小球落在坐标x处的概率密度为f（x），即落在区间x—x＋dx之间的概率为f（x）dx，由概率归一化条件，可得

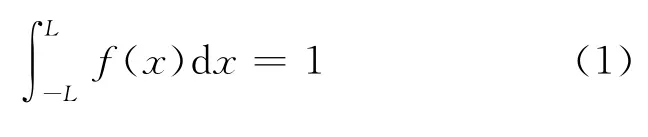
根据最大熵原理，信息熵S定义为

从入口处投入小球，则小球在下落过程中先后与许多钉子碰撞，最后落入某一狭槽.设各个小球落在板底的位置到入口处的距离平方的平均值为C，则有

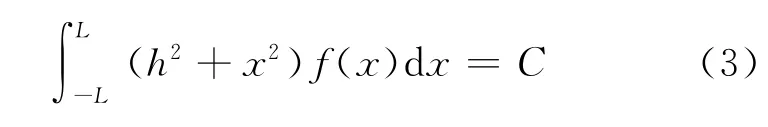
按照最大熵原理，小球在板底的分布应使得信息熵S在约束条件式（1）和式（3）下取得极大值，这类约束极值问题可使用拉格朗日乘子法解决.根据拉格朗日乘子法，引入函数：

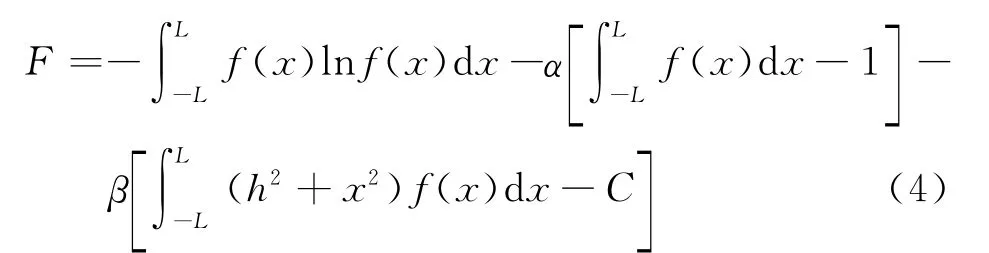
式中，α是由约束条件式（1）引入的拉格朗日乘子；β是由约束条件式（3）引入的拉格朗日乘子.

由δF［f（x）］＝0，可计算得信息熵S在约束条件（1）和式（3）下取极大值的概率密度函数f（x）为

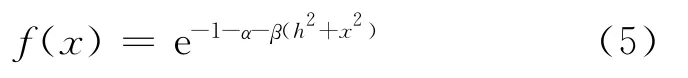
把式（5）代入式（1），得

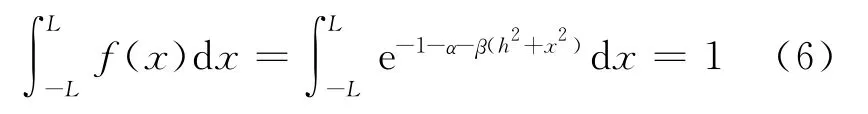
由式（6）得

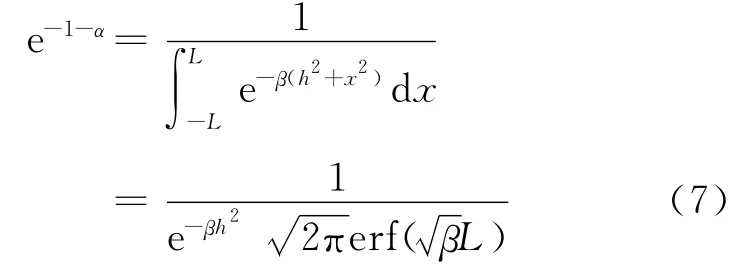
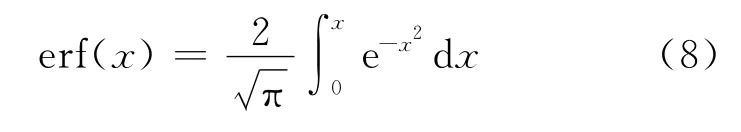
与不同x值对应的误差函数erf（x）的值可从一般积分表所附的误差函数表中直接查出［1］.

把式（7）代回式（5），即可得伽尔顿板实验中，小球分布的概率密度函数为

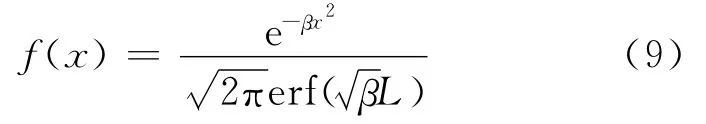
这样我们便使用最大熵原理推导出了伽尔顿板实验中小球理论分布的具体函数表达式.

3 计算机模拟伽尔顿板实验

计算机模拟实验是科学研究的重要手段，它可以克服真实实验中遇到的许多困难，弥补实验仪器不足的缺陷［9］.使用计算机模拟伽尔顿板实验可以方便地改变实验参数，便于反复进行多次实验，并快速得到实验结果.

我们使用Matlab语言编写了计算机模拟程序，对伽尔顿板实验进行了蒙特卡罗模拟，模拟的伽尔顿板实验装置形状如图1所示，钉子的总行数和每行的钉子个数均可调整.设共有m行钉子，奇数行的钉子数相同为2n-1个，偶数行的钉子数相同为2n个.从上向下统计行数，最上边的钉子为第一行，且第一行中间的那个钉子正对入口处，往下每行钉子交错排开.以第一行中间的钉子为坐标原点，沿着第一行钉子为x轴，向右为x轴正方向，竖直向下为y轴的正方向，建立坐标系.规定同一行中相邻两个钉子的距离为1，相邻的两行距离也是1，奇数行两端的钉子与板边的距离为1，偶数行两端的钉子与板边的距离为0.5；规定第一行中间钉子的坐标为（0，1），从入口处落下的小球第一次都和坐标为（0，1）的钉子相碰，即小球落到第一行时的坐标都为（0，1），在随后的下落过程中每个小球依次与下面的每行钉子中的一个钉子相碰，具体和哪个钉子相碰，由randn函数生成的一个正态分布随机数决定.模拟中小球总数取为N，定义一个N行×2列的矩阵，用来存放这N个小球的位置；矩阵中的每一行代表一个小球，矩阵的第一列用来存放小球位置的x坐标，第二列用来存放小球位置的y坐标.

现以小球从第一行下落到第二行为例说明一下模拟过程.当生成的随机数0≤randn＜n时，小球下落到第二行时位于它在第一行位置的右边，具体下落到哪个位置是这样规定的：当0≤randn＜1时，小球的横坐标加0.5，纵坐标加1；当1≤randn＜2时，小球的横坐标加1.5，纵坐标加1；……；当n-1≤randn＜n时，小球的横坐标加n-0.5，纵坐标加1.当生成的随机数-n≤randn＜0时，小球下落到第二行时位于它在第一行位置的左边，具体规定如下：当-1≤randn＜0时，小球的横坐标加-0.5，纵坐标加1；当-2≤randn＜-1时，小球的横坐标加-1.5，纵坐标加1；……；当-n≤randn＜-n＋1时，小球的横坐标加-n＋0.5，纵坐标加1.当生成的随机数n≤randn≤3n时，小球下落到第二行的位置规定为：当0≤randn-n＜1时，小球的横坐标为n-0.5，纵坐标加1；当1≤randn-n＜2时，小球的横坐标为n-1.5，纵坐标加1；……；当2n-1≤randn-n≤2n时，小球的横坐标为-n＋0.5，纵坐标加1.当生成的随机数-3n≤randn＜-n时，小球下落到第二行的位置规定为：当-1≤randn＋n＜0时，小球的横坐标为-n＋0.5，纵坐标加1；当-2≤randn＋n＜-1时，小球的横坐标为-n＋1.5，纵坐标加1；……；当-2n≤randn＋n＜-2n＋1时，小球的横坐标为n-0.5，纵坐标加1.当生成的随机数randn＞3n或randn＜-3n时，抛弃该随机数，令计算机再重新生成一个.小球从第二行下落到第三行等继续下落的过程依次类推.

在下面的模拟中，我们采用了如下设置：共有24行钉子（m＝24），奇数行的钉子数为21个（n＝11），偶数行的钉子数为22个.我们取了1 000 000个小球（N＝1 000 000），对它们在伽尔顿板中的下落过程进行了模拟，得到了小球频数按照落点位置分布的统计直方图，见图2.从图中可看出，在正对小球入口处（中央位置）的小球数目最多，离中央位置越远处的小球数目越少，分布形状近似于正态分布，但与正态分布有差别之处，正态分布的范围是从-∞到＋∞，而伽尔顿板实验中小球的分布由于受到板左右侧面的阻挡限制，分布范围是从板的左边缘到右边缘.

图2 小球落点频数统计直方图

4 理论推导结果与计算机模拟结果的比较

为了便于比较，我们把上述模拟得到的小球频数除以小球总数，转换为频率，从而得到了小球频率按照小球落点位置分布的数据，利用这些数据作出了小球频率按照小球落点位置分布的条形图，见图3.

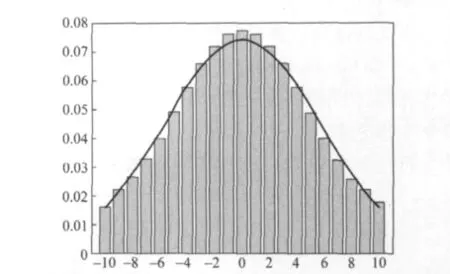
图3 小球概率分布理论曲线与计算机模拟的小球频率条形图的比较

把频率取自然对数，可得到小球频率的自然对数与小球落点位置间关系的数据.然后使用最小二乘法，对小球频率的自然对数与小球落点位置间关系的数据进行二次曲线拟合，拟合得到的二次曲线方程为

把我们导出的小球理论分布的概率密度函数式（9）两边取自然对数，得

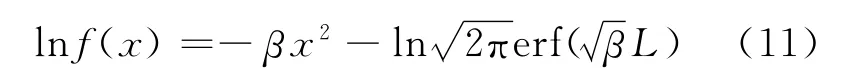
式（10）与式（11）比较，得到

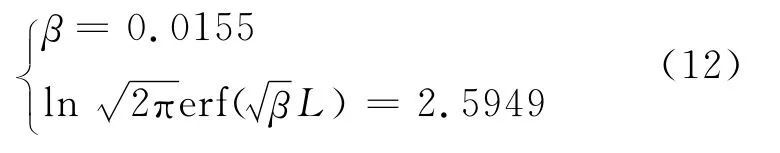
由上式可计算得

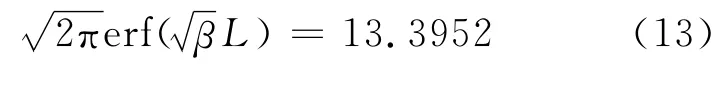
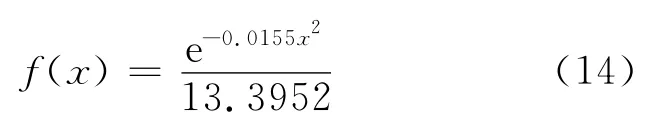
函数（14）为我们导出的小球理论分布概率密度函数的解析表达式，将此函数的关系曲线与小球频率按照小球落点位置分布的条形图作在同一张图上，见图3.由图3可见，理论导出的小球分布关系曲线（细线）与模拟得到的小球分布频率的条形图符合得较好.这说明我们使用最大熵原理导出的伽尔顿板实验中小球理论分布函数解析式较好地符合了实际情况.

5 结论

本文使用最大熵原理研究了伽尔顿板实验小球的分布，推导出了小球落点分布的概率密度函数解析表达式，见式（9）.接着使用蒙特卡罗方法对伽尔顿板实验进行了计算机模拟.通过把导出的小球理论分布概率密度函数解析式作成曲线，并把此函数曲线与小球频率按落点位置分布的条形图作在一起进行比较，发现二者符合得较好，这说明导出的小球分布函数解析式较为成功.

［1］李椿.热学 第二版［M］.北京：高等教育出版社，2008

［2］郝志峰，谢国瑞，汪国强.概率论与数理统计 第二版［M］.北京：高等教育出版社，2009

［3］彭芳麟.伽尔顿板实验的计算机模拟［J］.大学物理，2005，24（1）：45～49

［4］廖旭，任学藻.用二项式分布研究伽尔顿板实验的分布曲线［J］.实验科学与技术，2006，（1）：79～81

［5］聂燕.高尔顿钉板试验的算法实现及分析［J］.中国民航飞行学院学报，2008，19（3）：62～64

［6］Banavar J R，Maritan A，Volkov I.Applications of the principle of maximum entropy：from physics to ecology［J］.JournalofPhysics：Condensed Matter，2010，22：063101

［7］Plastino A，Curado E M F.Equivalence between maximum entropy principle and enforcing dU＝TdS［J］.PhysicalReviewE，2005，72：047103

［8］Jin H Y，Luo L F，Zhang L R.Using estimative reaction free energy to predict splice sites and their flanking competitors［J］.Gene，2008，424（1-2）：115～120

［9］彭芳麟.计算物理基础［M］.北京：高等教育出版社，2010