用《几何画板》研究电子在正交电场和磁场中的运动＊

余春日 余婧冰 张继椿

（1安庆师范学院物理与电气工程学院，安徽 安庆 246133）

（2中山大学翻译学院，广东 珠海 519082）

（3宿松县程集中学，安徽 宿松 246521）

1 引言

《几何画板》软件被誉为“21世纪的动态几何”，具有功能强大、形象直观、无须编程、简单易学等特点，已成为教学课件的优秀开发工具.它利用点、线、圆、计算器等很少几个基本工具即可实现任何图形的绘制和精确的计算，可以很好地辅助物理教学，在探究许多复杂物理问题如物理量的动态变化过程、光学中的物像关系、波的传播图像问题等方面有广泛的应用［1，2］.

带电粒子在正交电场和磁场中的运动是一个物理内容十分丰富的问题，文献［3，4］从物理的角度作了精辟的分析，特别是从运动和力的合成与分解的角度解决了带电粒子的轨迹问题，但是已有文献编制的具有动画效果的课件对C语言有较高的要求，显示带电粒子运动过程的直观性不够.本文以大学物理教材中的一道习题［5］为例，借助《几何画板》软件，直观形象地分析了电子在正交均匀电场和均匀磁场中的运动性质，描绘了电子在不同初始条件下形成的运动轨迹.

2 电子的运动方程

如图1所示，在空间有互相垂直的均匀电场场强为E和均匀磁场磁感应强度为B，B沿x方向，E沿z方向，一电子开始时从原点出发，以速度v0沿y方向前进.问电子运动的轨迹如何？

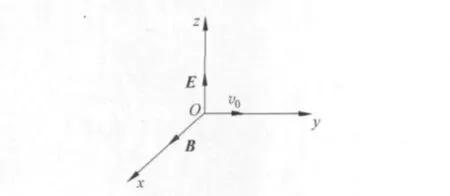
图1

解 电场和磁场分别为：

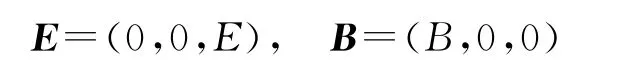
初始条件为：t＝0时，x0＝0，y0＝0，z0＝0；

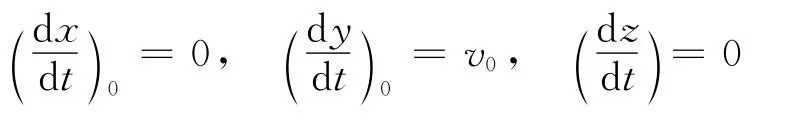
电子的运动方程为

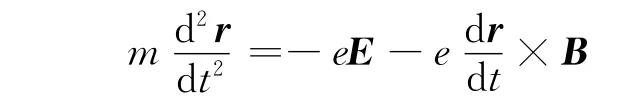
利用分量式和初始条件得［5］

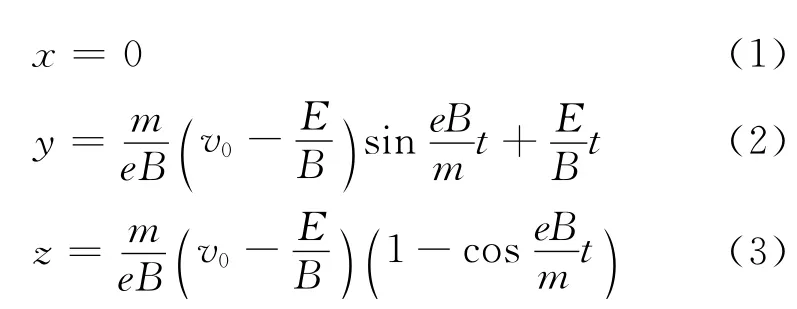
式（1）～式（3）表明，电子在yOz平面内作曲线运动，其轨迹的形状与v0、E和B有关.

3 讨论

3.1 电子的运动轨迹

为讨论方便，令

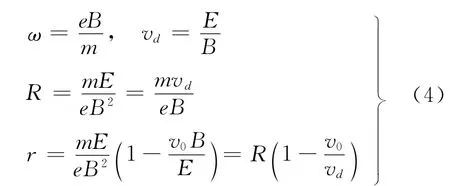
则式（2）、式（3）可改写为

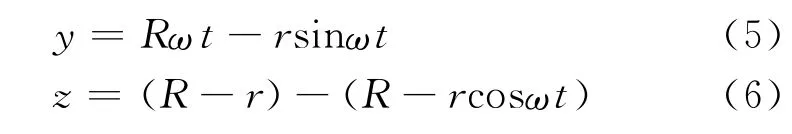
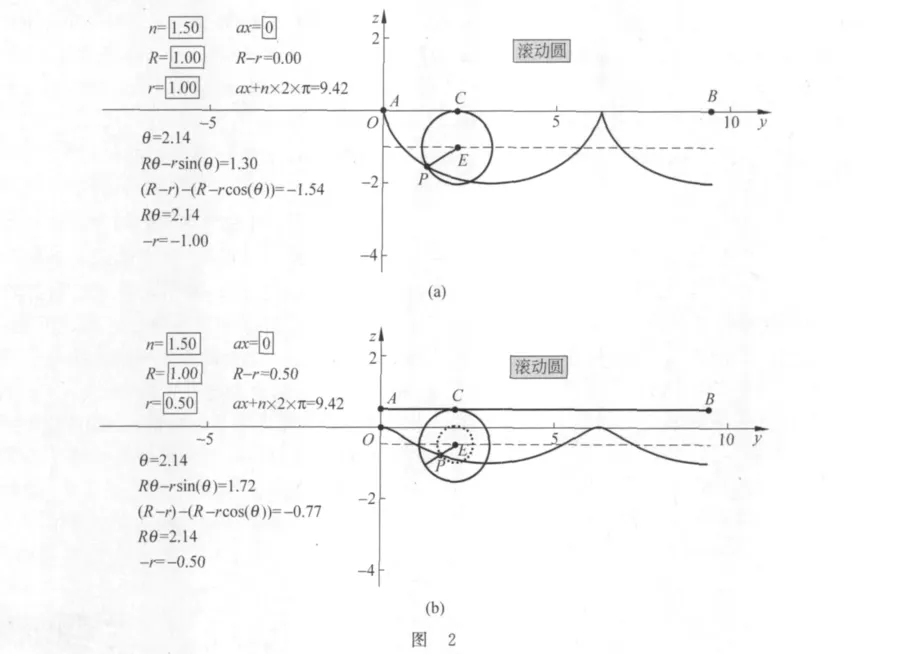
由式（5）、式（6）可知，电子运动的轨迹是半径为R的圆轮以角速度ω在定直线y＝R-r上作纯滚动时，轮上与圆心距离为r的固定点P描绘的摆线.

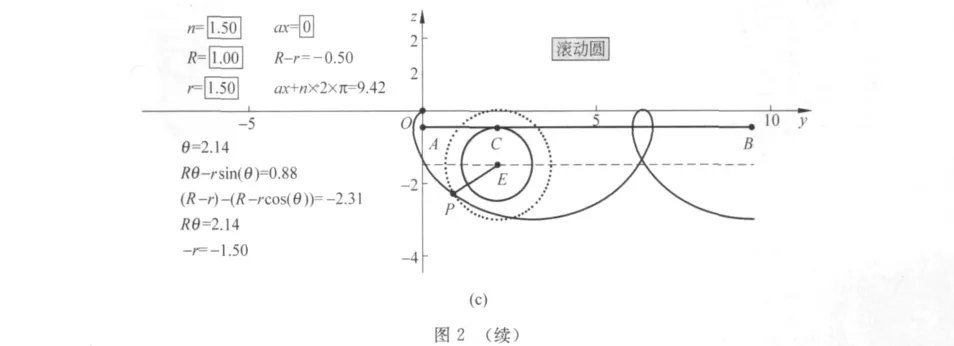
图2是以《几何画板》5.00制作的动画描绘的3种不同r情况下的摆线.若r＝R，P点位于滚动圆上，轨迹为等幅下摆线，如图2（a）所示（r＝R＝1）；若r＜R，P点位于滚动圆内，轨迹为短幅下摆线.如图2（b）所示 （r＝0.5＜R＝1）；若r＞R，P点位于滚动圆外，轨迹为长幅下摆线，如图2（c）所示 （r＝1.5＞R＝1）.图中显示的周期数（即圆轮滚动的圈数）是n＝1.5，只要电磁场的空间范围足够大，电子运动的轨迹将是一个接着一个的拱形弧线.

3.2 电子的运动性质

将式（5）、（6）两边分别对t求一阶导数，得电子运动的分速度

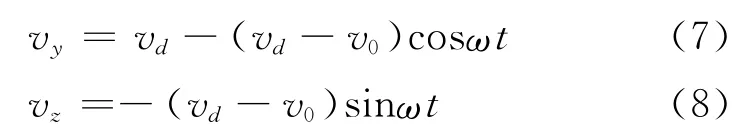
由式（5）～式（8）可知，电子的初速度v0可分解为沿y轴方向的速度vd和v′＝v0-vd（注意到r＞0时，v0＜vd，v′＜0），因此，电子的运动可看成是随滚轮圆心作速度为vd的匀速直线运动与绕圆心O′作半径为r、速率为vd-v0（角速度为ω）的逆时针匀速圆周运动的叠加，如图3所示.

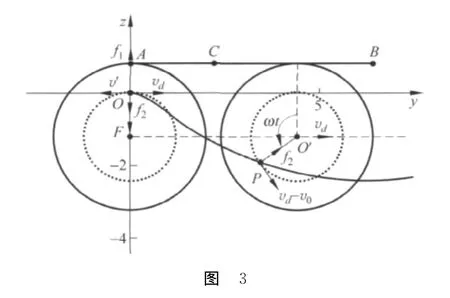
从动力学的观点看，电子沿y轴正方向作速率vd＝E／B的匀速直线运动，是电子受到向下的电场力F＝-eE和向上的洛伦兹力f1＝-evd×B平衡的结果，而电子绕圆心作逆时针匀速圆周运动是电子受到指向圆心的洛伦兹力f2＝-ev′×B作用的结果.

电子在轨迹最低点有最大速率

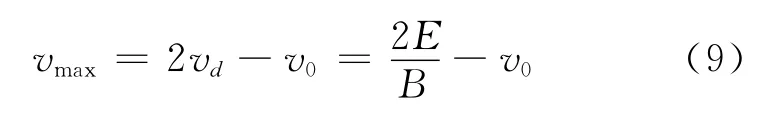
对应的位置坐标

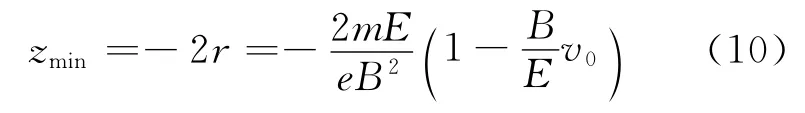
3.3 v0对电子运动摆线形状的影响

（1）当v0＝vd时，电子以速度vd沿y轴方向作匀速直线运动.

（2）当v0＝0时，r＝R，轨迹为等幅下摆线，如图2（a）所示.轨迹在最低点“平滑”，在最高点则变为“尖峰”.

（3）当0＜v0＜vd时，0＜r＜R，轨迹为短幅下摆线，如图2（b）所示.轨迹在最高点和最低点均“平滑”.

（4）当v0＜0时，r＞R，轨迹为长幅下摆线，如图2（c）所示.轨迹在最高点出现“回峰”现象.

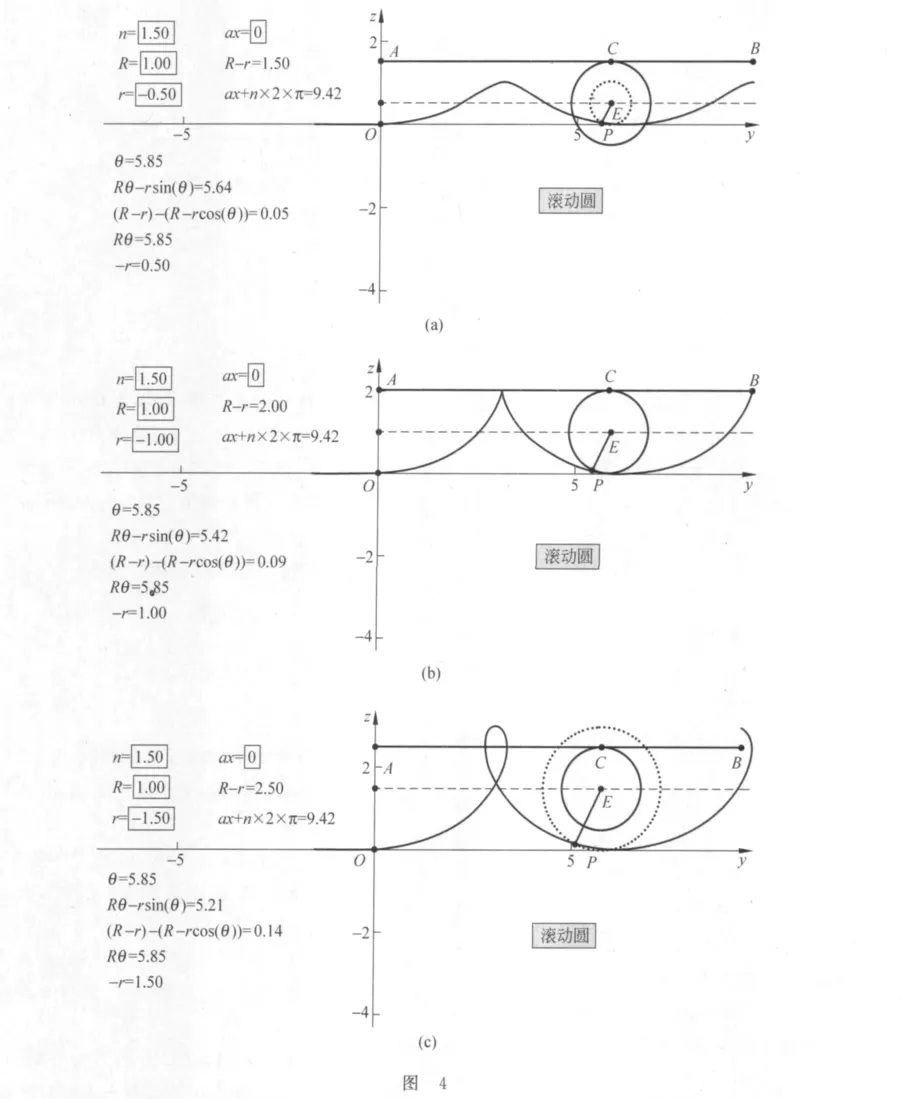
（5）当vd＜v0＜2vd时，-R＜r＜0，电子的运动轨迹是短幅上摆线，如图4（a）所示.轨迹在最高点和最低点均“平滑”.

（6）当v0＝2vd时，r＝-R，电子的运动轨迹是等幅上摆线，如图4（b）所示.轨迹在最低点“平滑”，而在最高点变为“尖峰”.

（7）当v0＞2vd时，r＜-R，电子的运动轨迹是长幅摆线，如图4（c）所示.轨迹在最高点将出现“回峰”现象.

4 结论

运用《几何画板》制作了电子在正交均匀电场和磁场中运动的动画，直观地展示了电子的摆线运动过程；分析了电子的运动性质和初速度对电子运动摆线形状的影响.可得出如下结论：

（1）电子的运动可看成是随滚轮圆心的匀速直线运动与绕圆心作逆时针匀速圆周运动的叠加.

（3）电子的运动摆线在最低点和最高点的形状，取决于在最值点的合速度.若在最值点的合速度水平向右，则摆线在此处“平滑”；若在最值点的合速度为零，则摆线在此处为“尖峰”；若在最值点的合速度水平向左，则摆线在此处出现“回峰”.

本文的研究结果很容易推广到带电粒子在重力场、电场和磁场形成的复合场中.教学中可鼓励学生用《几何画板》把一些物理问题做成动画，引导学生探索解决，这对于培养学生的学习兴趣，感悟科学研究方法，提高思维品质具有重要意义.

［1］刘成华.运用几何画板探究动态物理问题的策略研究［J］.物理通报，2007，（10）：43～45

［2］朱亚.利用“几何画板”解决物理疑难问题［J］.物理教师，2007，28（4）：40～41

［3］蒋晨曦，过祥龙，刘军.带电粒子在正交电磁场中运动分析及运动轨迹的计算机描绘［J］.物理与工程，2001，11（4）：39～44

［4］张九铸.带电粒子在正交电场和磁场中轨迹的形成及曲率半径［J］.大学物理，2011，30（5）：35～38

［5］赵凯华，罗蔚茵，陈熙谋.新概念物理题解（上册）［M ］.北京：高等教育出版社，2009