量纲分析及其应用

严导淦

（同济大学物理教研室，上海 200092）

在当前理工科专业的物理课程和教材中，对“量纲”内容的介绍一般都比较少.有的即使教材中有所介绍，课程教学中也很少讲授.实际上，对理工科学生来说，量纲分析及其方法，在有关专业的今后工作中是很有用的.它不仅可以找出某些物理量与另外一些物理量之间的关系；用于物理量的单位换算；检验公式的正确与否；还可以借以探究某些物理规律，有助于建立起函数关系的基本形式.

由于物理现象一般较复杂，涉及的因素很多，有时无法列出描述物理现象的微分方程；或者求解这些方程在数学上有困难，因而不得不乞助于其他分析途径或实验来解决.量纲分析在科技实践中是进行分析和实验的一种有效的手段.通过量纲分析，一般来说，可以合理而有目的地简化实验，并有助于整理实验成果.

当然，要正确应用这一方法，还必须根据已有的科技知识和理论，对物理现象具有一定的分析能力.

本文就量纲分析问题作一简介，旨在引起同行们的重视和共析.

1 量纲

度量物理量的单位的类别叫做量纲.例如小时、分、秒是不同的时间测量单位，它们都属于同一时间种类，可以统一用T表示，则［T］①按照GB 3103—93文件规定，某个物理量X的量纲用dimX表示，考虑到国际物理学界的使用习惯和便于查阅历史文献，本文沿用［X］表示。就是上述时间单位的“量纲”.

在国际单位制（SI）中，取长度、质量、时间、热力学温度、电流、物质的量、发光强度这些物理量作为“基本量”，来表述物理现象及其运动规律.它们的量纲分别用［L］、［M］、［T］、［Θ］、［I］、［N］、［J］表示，叫做基本量纲.而其他一些物理量的量纲是根据有关的物理定义或定律，借上述这些基本量纲导出的，这些量纲就是相应于“导出量”的“导出量纲”.

基本量纲与其他基本量纲之间是相互独立的，即一个基本量纲不能从其他基本量纲导出.例如我们不能从［L］、［I］中得出［M］，也不能从［T］、［M］中得出［L］；但［L］、［M］和密度的量纲［ρ］三者则非相互独立的，因为［ρ］＝［L-3M］.

其次，基本量纲并没有规定必须取几个.例如在工程力学问题中，任一力学量的量纲一般取［L］、［T］、［M］为基本量纲；但也可以选用四个互不相关的基本量纲［L］、［T］、［M］及力的量纲［F］，即将［F］作为独立的基本量纲.这时需将牛顿定律写成F＝kma，而系数k的量纲则为［k］＝［FT2M-1L-1］.

一般来说，引入一个额外的物理系数，就可以增加一个相互独立的基本量纲.过去工程上常采用［L］、［T］、［F］作为基本量纲，而今在力学中，已统一用［L］、［T］、［M］作为基本量纲.

导出量的量纲或物理方程中有量纲的常量均可用基本量纲的指数乘积形式表示，例如，借1摩尔的理想气体状态方程pV＝RT，可得R的量纲为［M1L2T-2Θ-1］.在力学中，任一物理量X的量纲均可用三个基本量纲［L］、［T］、［M］的指数乘积形式表示：

上式就是力学中的量纲公式，量X的性质可由量纲指数α、β、γ来反映.如α、β、γ中任一个不等于零，则说X是一个有量纲的量.在力学中，有量纲的量大致可分为三类：

（一）α≠0、β＝0、γ＝0为一几何量；

（二）α≠0、β≠0、γ＝0为一运动学的量；

（三）α≠0、β≠0、γ≠0为一动力学的量.

例如面积A的量纲为长度量纲的平方，即［A］＝［L2］，或写成量纲公式［A］＝［L2T0M0］.加速度的量纲公式为［a］＝［LT-2M0］，由于F＝ma，可知力F的量纲公式为［F］＝［M LT-2］.

2 无量纲的数——纯数

有的物理量，其量纲为零.例如式（1）中各指数α＝β＝γ＝0，或

则X称为无量纲数或纯数，即只表示某个数.

无量纲数可以是两个相同量的比值（例如，体积V的相对压缩量，即为一个无量纲数）.也可以由几个量纲通过乘、除而组成，而组合结果的各个基本量纲的指数为零，满足式（2）.

例如，流体力学中区别层流和湍流的一个判据，即雷诺数（Reynold’s number，其中流体速度v的量纲为［LT-1］，管子直径d的量纲为［L］，流体的运动粘度系数γ的量纲为［L2T-1］，则雷诺数的量纲为

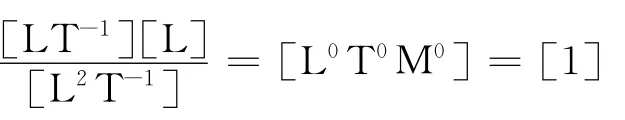
即为无量纲数.

无量纲数有下述重要性质：

（1）无量纲数既无量纲又无单位，其数值大小与所选用的单位制无关，因而它可作为一个客观的判据值.例如表征流体的某一流动状态的雷诺数为Re＝2000，则不论采用SI制或英制单位，其值均保持不变.所以，雷诺数可作为一个客观判据.

（2）一切有量纲的物理量都将因选取不同单位制而有不同数值.若用有量纲的物理量来表示一个物理规律的自变量，则此物理规律所表达的因变量也将随所选用的单位而有不同的值.而单位是人为选用的，可是物理规律不应随主观意志而改变.只有无量纲量不随所选用的单位的不同而改变其值，所以要正确反映物理规律，最好将其物理量组合成用无量纲数表示的形式.或者说，一个完整、正确的物理方程应是用无量纲项组成的方程.由此可见无量纲数的重要性.量纲分析的目的之一就是要找出正确地组合无量纲数的方法.

（3）在对数、指数、三角函数等任何超越函数运算中，都必须是对无量纲数来进行的.例如，理想气体等温压缩过程中的功为

体积的压缩比即为一无量纲数，故可取对数；而对有量纲的某些物理量取对数是无意义的.又如平面简谐行波的表达式为

又如对物理现象中的自然衰减或增长过程，乃指过程中某一个量在确定的空间或时间间隔中的变化为其自身的一个恒定的分数，即可表示为微分形式

其中，N为变化着的量，α是常数，正负号分别表示增长或衰减.因此，变化率正比于测量这个变化率时N的值.积分上式得N＝N0e±αx或N＝N0e±αt，其中N0是N在x＝0或t＝0时的值，e是自然对数的底.这里不管对数的底e的指数是什么，它总是底数为e的自乘次数，所以这个指数函数e±αx或e±αt是无量纲数，即α的量纲和x-1或t-1的量纲一样.

3 量纲分析的基本原理

凡是正确反映客观规律的物理方程，其各项的量纲均须一致，这是量纲分析的一条基本原理，称为量纲和谐原理.因为只有量纲相同的物理量才能加减；否则，把不同量纲的物理量相加减，例如把力和电流相加显然无意义.所以，一个方程中各项的量纲必须相同和一致.但不同量纲的物理量可以相乘、除，可得出导出量纲表示的另一个物理量，如质量乘速度可得动量.

量纲和谐原理在科研中有广泛应用，例如：

（1）一个物理方程在量纲上是和谐的，则方程的基本形式不因换用量度单位而改变.借量纲和谐原理，可用来检验所建立的方程或检验公式是否完整.例如三维的波动方程为

式中，S为位移，u为波速.上式各量的量纲均为［T-1］，因而此式的量纲是和谐的.不论用什么单位制，该方程的形式均不变；如果用方程中任一项去除式中各项，则可得到无量纲组成的方程式.

如果一方程不论是代数方程或微分方程在量纲上不和谐，则就得检查一下方程是否完整，所用单位是否一致，在数学推导中是否有误.

正确的物理方程固然要求量纲和谐，但在工程技术中，例如研究江河中泥沙运动的规律时，也有一些方程的量纲是不和谐的.这一般是指单纯借实验观测资料所建立的经验公式，它们在应用上是有局限性的.不过，随着科学技术的不断发展，可以期待，它们终究要被符合量纲和谐原理、且正确反映客观规律的公式所取代.

（2）借量纲和谐原理建立物理方程，乃是量纲分析的方法之一，称为瑞利（Lord Rayleigh）法则，它适用于较简单的问题.

例1 在真空中质量分别为M1、M2的两个物体间的万有引力为为引力常量，r为两个物体间的距离.设M1≫M2，则M2在引力作用下将近似地以M1为中心沿圆轨道运动.

解 今用瑞利法则求物体M2沿轨道运行的周期τ.经分析，影响M2运动速度的物理量可能有M1、M2、r和G.但M2的影响可忽略，因为M2增大一倍，引力也增大一倍，这使物体M2之法向加速度（v2／r）维持不变；G虽为常量，但不能从影响因素中去掉.因为M1和r中都不含时间的量纲，所以周期τ不可能只是M1和r的函数.这表明，影响因素不一定都是变量.于是有如下的函数关系：

一般可将上述函数关系用指数的乘积形式来表示：

式中k为某一无量纲常数系数.从万有引力公式，得［G］＝［M-1L3T-2］，则上式的量纲关系式为［T］＝［M］α［L］β［M-1L3T-2］γ，按量纲和谐原理，得

联解上列三式，得

最后结果为

例2 根据实验结果所得的数据分析，单摆的周期T可能与摆球的质量m、摆长l、摆角θ有关；并考虑到单摆处于恒定的重力场中，还与重力加速度g有关.于是，有如下的待定函数式

根据量纲和谐原理，由于上述这些量的量纲不同，它们不能相加减.因而，一般可假定上述函数关系具有这几个量的幂次的乘积形式，写作

式中，α、β、γ、δ为待定指数.把上式中的各量的量纲用力学中的基本量纲L、M、T表示，并且θ是量纲为1的数，则上式的量纲关系式为

上式左边的周期T，其量纲是时间T，即［T］＝T.于是，按量纲和谐原理，为了使上式两边的量纲相同，其中同一基本量纲的指数应相等，从而有

联立求解，得

把它们代入式（b），可得单摆的周期为

其中，量纲为1的系数θδ是摆角θ的函数，令Φ（θ）＝θδ，而Φ（θ）是无法用上述量纲分析方法给出的，可借实验或其他途径确定.

例3 求水波的波速公式.

解 根据水工实验室测定的实验数据分析可知，浅水波的波速v浅与水深h和重力加速度g有关；而深水波的波速v深与波长λ和重力加速度g有关.

对浅水波而言，令

式中，a为一无量纲常数系数；α、β为待定指数.上式的量纲关系为

按量纲和谐原理，上式中的量纲指数应满足

联解上式，得将α、β值代入式（a），得

从理论上推算，可得系数a＝1，于是浅水波波速公式为

对深水波而言，同理可借量纲和谐原理，读者可自行推得

值得指出，在观察或分析一个物理现象时，应尽可能地列举出与该现象有关的主要变量（例如，例2中的式（a））；否则将直接影响分析结果的真实性.这是首要的、也是较困难的一步，往往取决于人们的实验或理论水平，以及对所研究现象的分析能力.

4 量纲分析法的普遍理论——π定理

π定理是量纲分析的主要内容.这定理可叙述如下：

任何一个物理过程，如果包含有n个物理量，涉及m个在量纲上相互独立的基本量纲，则这个物理过程可由n个物理量组成的（n-m）个无量纲数所表达的关系式来描绘.因这些无量纲数用π来表示，故称此定理为π定理（证明从略）.

设影响物理过程的n个物理量为X1、X2、…Xn，则此物理过程可用一完整的函数关系式表述：

设这些物理量包含有m个在量纲上相互独立的基本量纲，按π定理，这个物理过程可以用（n-m）个无量纲的组合量π表达的关系式来描述，即

应用π定理的步骤如下：

（1）观察和分析所研究的物理现象，确定影响这一现象的各个物理量，即写成式（3）.此处所说的有影响的物理量，是指对所研究的现象起作用的所有各种独立因素.例如，研究声波的传播，主要包括介质的物理性质、边界的几何特性、波动的运动特征等.影响因素（可为变量，也可为常量）列举得是否全面和正确，将直接影响分析的结果.这是首要的，也是较困难的一步，只能凭借人们对所研究现象的深刻认识和全面理解来确定.

（2）从n个物理量中选取m个基本物理量，作为m个基本量纲的代表.m一般取3.因此要求这三个基本物理量两个是独立的，即这三个物理量不能组合成一个无量纲数.设表示基本物理量X1、X2、X3的量纲式为

则X1、X2、X3不能形成无量纲数的条件为

（3）从三个基本物理量以外的物理量中，每次轮取一个，与这三个基本物理量相除（也可相乘），组合成一个无量纲的π项，这样一共可写出（n-3）个π项：

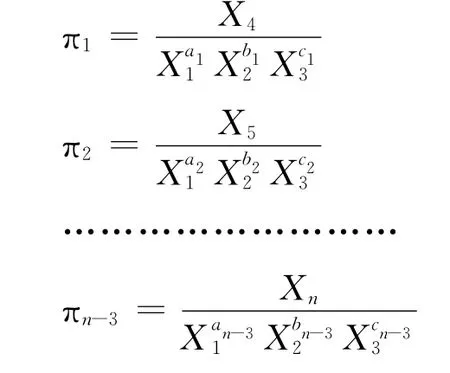
式中，ai、bi、ci为各π项的特定指数.

（4）每个 π 项即是无量纲数，即 ［π］＝［L0T0M0］.因此，可根据量纲和谐原理求出各π项的指数ai、bi、ci.

（5）写出描述现象的关系式

这样，就把一个具有n个物理量的关系式简化为（n-3）个无量纲数的表达式.如前所述，无量纲数才具有描述自然规律的绝对意义.所以式（5）才是反映客观规律的正确形式.而且也是进一步分析研究的基础.

例4 如例4图所示，一直径为d、密度为ρ的圆球，在充满密度ρ1、粘度μ1的无限介质中沉降.影响其沉降速度v的因素有d、ρ、ρ1、μ1（其量纲为［ML-1T-1］）及重力加速度g.今用π定理确定沉降速度的关系式.

例4图

解 按题设的影响沉降速度v的因素，列出n＝6个物理量的关系式为

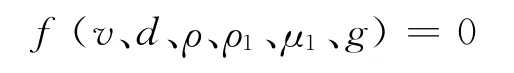
在上述6个物理量中选取3个基本物理量：圆球直径d（代表现象的几何尺度）；沉降速度v（代表现象中的运动学特征）；圆球密度ρ（代表圆球物性）.这三者包括了L、T、M三个基本量纲，有如下的量纲式

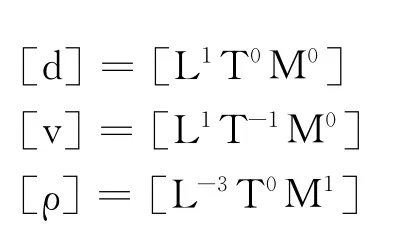
各指数项的行列式

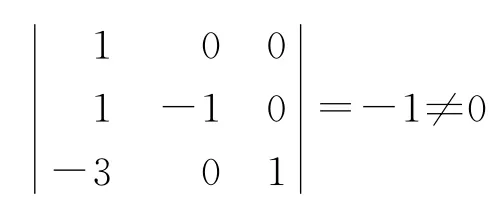
即这三个基本物理量的量纲是独立的.

于是，可写出n-3＝6-3＝3个无量纲π数：

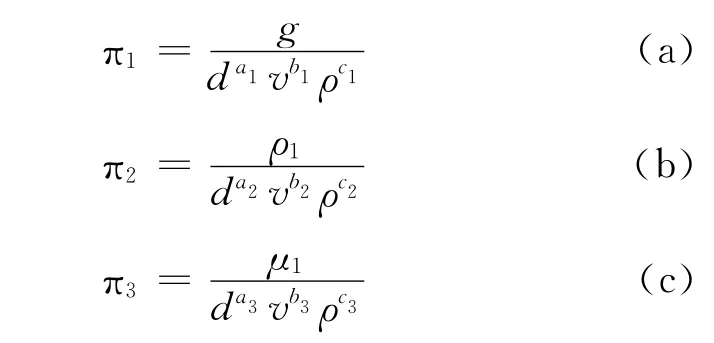
按量纲和谐原理，各π数的指数可确定如下：以式（a）的量纲式为例，有

得

对上述三式联解求得，a1＝-1、b1＝2、c1＝0，于是，有

同理可求得

将各π项代入公式（5），得无量纲方程为

或将上式的隐函数式改写成下列的显函数式

最后得沉降速度v的关系式为

通过量纲分析的π定理，得出圆球沉速公式的基本形式，即断定了成正比，并从无量纲函数f1知道了影响沉速的两方面因素（反映介质对圆球的浮力）和（反映介质因其粘性引起的阻力），从而找到了进一步研究问题的途径.

综上所述，借量纲分析方法，不仅可以在已知物理过程有关的物理量情况下，借量纲和谐原理或π定理获得各物理量之间的基本关系式，并找出深入研究该问题的途径，而且可以使一些经验公式具有理论上（量纲和谐性）正确的形式.因此，量纲分析法在科技领域（物理学、流体力学和工程学等）内常常作为一个有效的研究手段，而被广泛地应用着.

鸣谢：

本文叼蒙王祖源教授和陆汝杰高级工程师审定和匡正，谨表谢枕.

［1］E.dost.Q.Isaacsen.Dimensional Methods in Engineering and Physics，1975年

［2］清华大学水力教研组编.水力学［M］.人民教育出版社，1981

［3］严导淦，王晓鸥，万伟编.大学物理学［M］.机械工业出版社，2012

［4］钱宁，万兆惠著.泥沙运动学［M］.科学出版社，1983