MIMO雷达正交相位编码信号设计及分析

张远安 张春荣 强 勇

(西安电子工程研究所 西安 710100)

1 引言

MIMO雷达是近些年雷达研究中新提出的一种新体制雷达，它能够有效地改善现代雷达的性能，在雷达抗干扰、低截获等方面具有良好的性能而被广泛研究［1］。MIMO雷达为了避免多发的信号通道之间相互干扰，要求发射信号是相互正交的，这也就意味着发射信号之间应具有较小的互相关值。同时，MIMO雷达为了获取更高的距离分辨率，要求发射信号自相关函数应具有较低的旁瓣。

采用相位编码信号设计MIMO雷达信号，在文献［2～5］中都有研究，其原理是一样的，只是在构造代价函数和优化方法上略有不同。本文首先对相位编码信号设计MIMO雷达信号波形原理进行说明，然后产生一组相位编码信号，并用遗传算法［8］进行优化，获取所需的相位编码信号组，最后分析该组信号的自相关函数和互相关函数性能，验证其正交性，最后分析信号码长、信号个数、信号的相位数对MIMO雷达相位编码信号设计的影响。

2 正交相位编码信号设计的原理

由于MIMO雷达发射信号之间是正交的，所以采用相位编码信号设计MIMO雷达信号波形，最重要的是各发射信号之间满足正交性。假设MIMO雷达系统包含L个发射天线，每个发射天线都从正交码集{sl(t)，l=1，2，…，L}中选择一组作为它的发射信号，每个信号的码长为N，相位编码为M相编码。为了满足各发射信号之间正交的条件，要求每个发射信号的互相关函数为0，而自相关函数接近于一个冲击函数，设计该组相位编码信号，正是基于此思想。设第l个信号为:

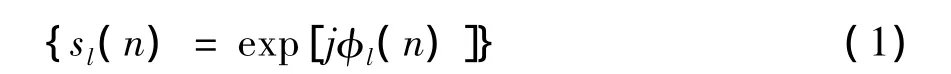
式中:n=1，2，…，N;l=1，2，…，L。

编码相位取为:

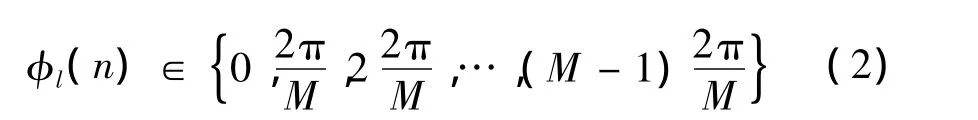
所以，整个码组信号矩阵可以表示为:

根据发射信号正交的思想，并联合码组信号矩阵S，可得正交相位编码信号的自相关函数和互相关函数应该同时满足以下条件:

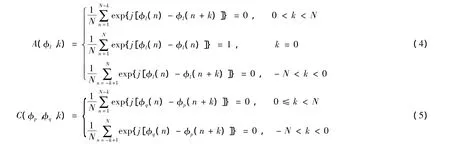
式中:l=1，2，…，L;p ≠ q;p，q=1，2，…，L。

综合考虑上述要求，正交码组的设计就转化为求在上述两个约束条件下构造矩阵S(L，N，M)的问题。一种有效的方法就是通过最小化目标函数来寻找最优相位序列。设计正交相位编码时，目标函数可以设为:

又因为:

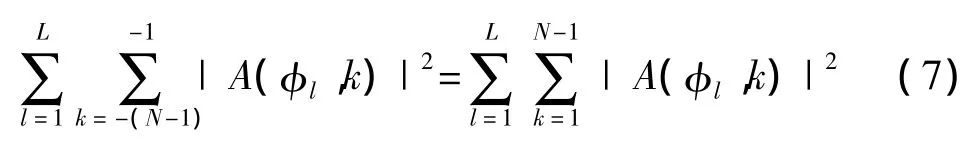
所以，可以把目标函数修改为:

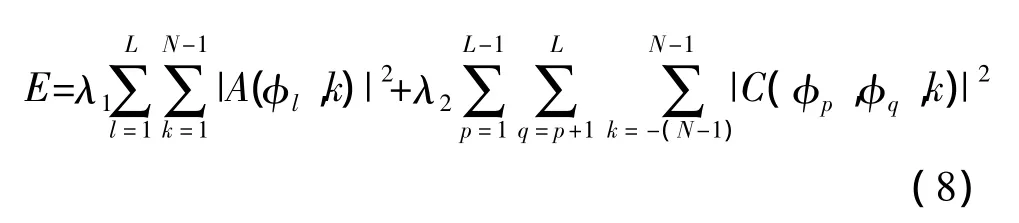
其中λ1=λ'1+λ″1。从式(8)中可以看出目标函数为自相关旁瓣能量与互相关能量之和。λ=［λ1λ2］为目标函数的加权系数。对于给定的L、N、M，最小化式(8)将产生一组满足条件(4)和(5)的正交相位序列。可以采用遗传算法来优化目标函数从而获取所需的正交相位码。

3 遗传算法优化相位编码信号步骤

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。遗传算法适用于解决复杂的非线性多目标优化问题且其具有自适应的特点，可使优化结果得到全局最优值，避免陷入局部值，所以本文采用遗传算法对信号进行优化设计，其运算流程图如下图1所示。

图1 遗传算法优化设计运算流程

根据图1，其具体过程如下:随机产生K组(K为遗传过程中初始个体数)相位编码信号(每组信号中含有L个信号，每个信号的码长为N，信号为M相编码)，并对相位码信号进行编码，产生的K组信号码作为初始值，称作种群1。然后计算该K组中每个码组信号的适应函数值，看是否满足循环结束的条件，满足则停止，不满足则再用遗传算法对K组码组信号进行优化，优化后得到的K组信号码组称为种群2，把种群2赋予种群1，再次重复刚才的步骤，直到循环结束，获得K组优化的信号码，对其进行解码，并从其中选择使目标函数式(8)最小的信号码组作为所需的信号码组。

4 相位编码信号设计结果及分析

4.1 信号的正交性分析

假设发射天线个数为4，发射信号为四相编码信号，信号长度为 128，即 L=4，N=128，M=4。采用遗传算法优化，遗传1000代，所需的最优解变化和种群均值的变化情况如图2所示。

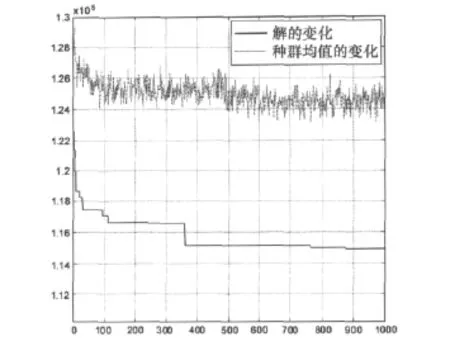
图2 种群遗传优化解的变化

从图2中可以看出，经过1000次遗传优化，所需的最优解，即代价函数最小值一直在减小，最后趋于稳定，优化得到的信号如表1所示，其中编码0、1、2、3 分别对应着相位为

表1 优化得到的四相编码序列

优化得到的四相码信号的非周期自相关和互相关函数特性如图3和图4所示。

优化得到的正交四相码的自相关旁瓣峰值(ASP)和互相关峰值(CP)如表2所示。

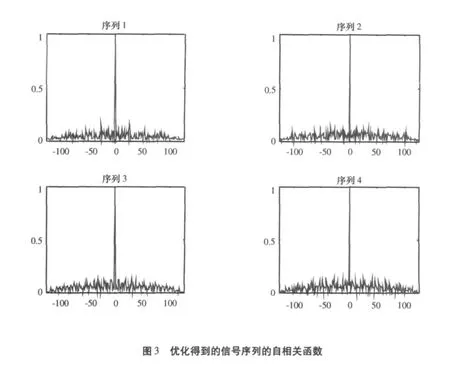
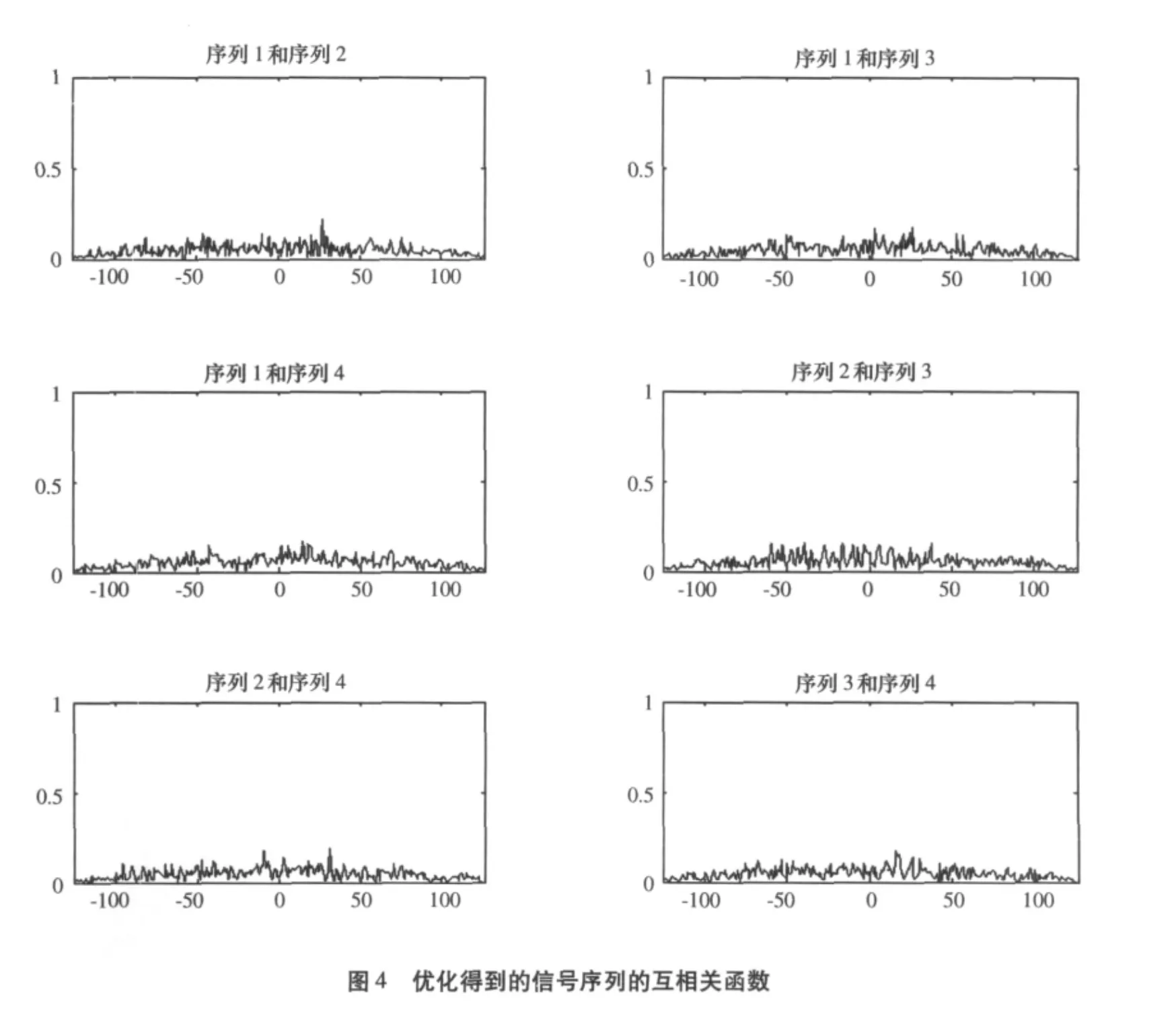
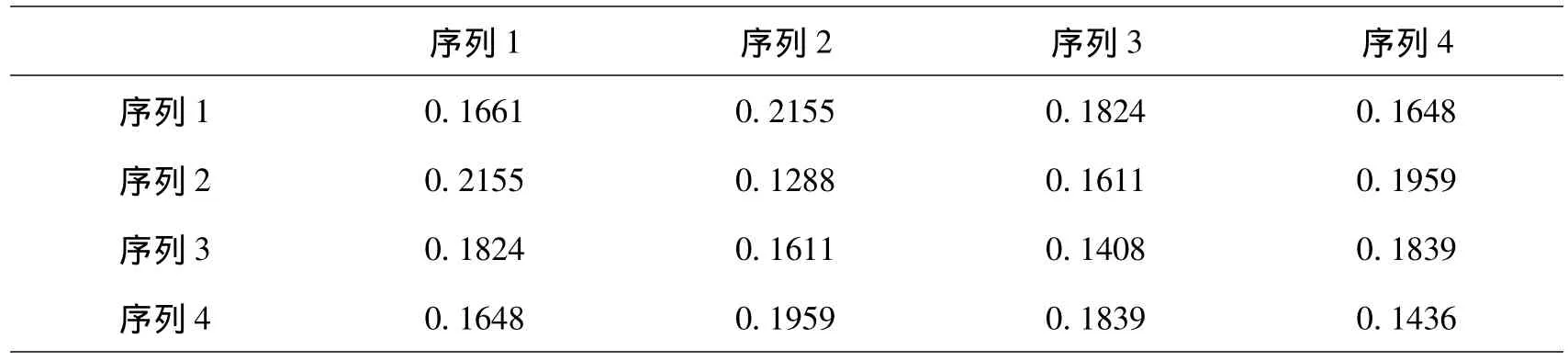
表2 正交四相码的ASP和CP(L=4，N=128，M=4)

平均自相关旁瓣峰值和平均互相关峰值分别为0.1448和0.1839。可以看出，信号序列的自相关函数旁瓣值和互相关函数值都较小，但都不为0，这是因为完全正交的相位编码信号序列是不存在的，信号设计的目的就是要使信号序列的自相关函数旁瓣值和互相关函数值之和最小。

4.2 码长对信号性能的影响

对于传统的脉冲压缩信号，如M序列或者Frank多相码，其自相关旁瓣峰值随码长N的增加，以1/的速度降低。同样，对于多相序列，更大的码长将使代价函数有更大的自由度，因而能得到更好的优化结果。图5所示为平均ASP和平均CP随码长N(16≤N≤1024)的变化曲线，其中信号序列个数L和相位数M固定为4。从图中可以看出，ASP和CP按照曲线o(1/)，随着码长N的增加，以1/的速度降低。所以码长好的信号序列，其性能更好，但是考虑到信号序列设计的难度，码长的选择要适当。

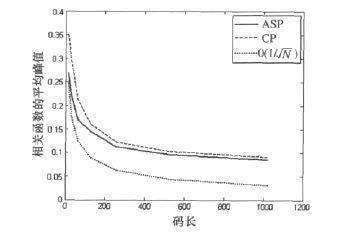
图5 平均ASP和平均CP随码长变化曲线(L=4，M=4)

4.3 信号个数对信号性能的影响

对于MIMO雷达，每个通道发射一个信号，信号的个数即为发射通道的个数。图6所示为平均ASP和平均CP随信号个数L的变化曲线，当固定M和N时，可以看出随着信号个数L的增大，平均ASP和平均CP将增大，不过增大很小，这表明可以通过优化设计得到比较多的正交信号。正是基于这一点，也给MIMO雷达设计正交相位编码信号提供可能。

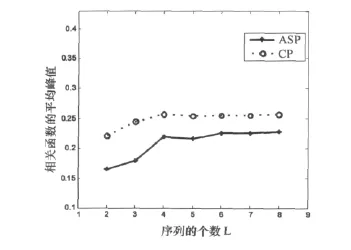
图6 平均ASP和平均CP随信号个数变化曲线(M=4，N=40)

4.4 相位个数对信号性能的影响

增加可用相位数M，在优化中将会有更大的自由度，可以促进设计结果。图7所示为平均ASP和平均CP随M的变化情况，可以看出M从2到8变化时，ASP和CP值轻微降低。考虑到多相码设计的困难，所以四相码是个不错的选择。

图7 平均ASP和平均CP随相位个数M的变化曲线(L=4，N=40)

5 结束语

本文在了解MIMO雷达发射正交信号的基础上，采用相位编码信号设计MIMO雷达的正交波形，通过分析其原理，构造目标函数，设计产生一组相位编码信号，再采用遗传算法对其进行优化，然后通过分析其自相关和互相关特性，并验证了这样设计的信号具有很好的正交性能。在设计产生正交相位编码信号的基础上，分析了信号码长、信号个数、信号的相位数对雷达性能的影响，这些在用相位编码信号设计MIMO雷达发射信号中都是必须考虑的问题，通过分析这些因素，为MIMO雷达在发射信号设计方面提供了一定的理论支持。

［1］强勇，张冠杰，李斌.MIMO雷达进展及其应用研究［J］.火控雷达技术，2010，39(1):1-10.

［2］Hai Deng，Polyphase Code Design for Orthogonal Netted Radar Systems［J］.IEEE Transaction on signal Processing，2004，52(11):3126-3135.

［3］张宇，王建新，孙锦涛，MIMO雷达的相位编码信号设计［J］.兵工学报，2010，31(1):109-112.

［4］吕红芬，宋万杰，张子敬等，基于遗传算法和贪心算法正交多相码设计［C］.第十一届全国雷达学术年会论文集，2010.11:377-381.

［5］李明，郝明，基于混合遗传算法的正交相位编码波形设计［J］.电子工程师，2007，33(10).

［6］陈金立.相位编码MIMO雷达信号处理技术研究［D］.南京理工大学博士论文，2010.

［7］刘波.MIMO雷达正交波形设计及信号处理研究［D］.电子科技大学博士论文，2008.

［8］雷英杰，张善文，李续武等.MATLAB遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2004.