具有初始随机材料缺陷的非晶合金剪切带模拟

易 敏 沈志刚

(北京航空航天大学 航空科学与工程学院，北京100191)

郭瑶峰

(北京航空航天大学 材料科学与工程学院，北京100191)

非晶合金是金属熔融物在急速冷却下形成的一类新型合金，因其原子排列长程无序、短程有序的结构特点，而呈现出与普通晶体合金迥异的性能.比如非晶合金高强度、高硬度、耐磨、高弹性比功等优异的力学性能［1－2］，使其在工程结构领域展现出广阔的潜在应用前景.但是，在塑性性能上，与其他普通工程结构材料相比，非晶合金存在致命的缺点.研究表明，非晶合金在高温下呈现粘性流动的均匀变形，而在室温下呈现非均匀变形，塑性变形高度局部化于极窄的剪切带内，导致非晶合金在断裂前呈现出非常有限的塑性变形，这极大地限制了非晶合金的应用［3－4］.剪切带作为非晶合金塑性变形的载体，决定着非晶合金的宏微观塑性行为，对剪切带的研究一直是非晶合金领域的一个热点.一些研究人员在通过增加剪切带数量和密度、施加约束阻碍剪切带扩展、促进剪切带相互影响等实验方法提高非晶合金塑性上做了大量工作［5－7］，但是仅仅依赖于反复实验来研究非晶合金剪切带，不免费时费力，经济上也不合算，而数值模拟往往能发挥补充作用.

剪切带实际上是应变软化导致局部化变形的结果，在非晶合金的真实试样中，微小剪切带初始化的位置和主剪切带形成的位置，是由试样的缺陷分布决定的，而在数值模拟中，剪切带的出现是数值扰动的结果.因此，在模拟剪切带时，如何给数值模型施加缺陷显得相当重要.以往的剪切带模拟研究一般采用统计分布的内聚力缺陷、某个位置的自由体积或弹性常数缺陷、几何缺陷等等［8－10］，但是描述非晶合金塑性变形微观机制的自由体积理论［3］表明，非晶合金剪切带是与自由体积演化过程密切相关的，因此将自由体积作为缺陷参数对剪切带的模拟更合适.另外实际铸造出来的非晶合金自由体积缺陷的分布也是随机的，所以采用随机自由体积缺陷来定义随机材料缺陷显得更接近真实情况.

本文首先对非晶合金试样做了压缩实验，然后基于自由体积作为内部参量的本构模型和平面应变模型，以初始自由体积作为初始随机材料缺陷参数赋予材料，模拟了在初始随机材料缺陷下非晶合金剪切带行为.结果表明本文模拟工作能很好地捕捉到非晶合金剪切带的主要特征，对研究非晶合金剪切带机制及通过控制剪切带来提高塑性具有一定指导意义.

1 本构关系

图 1 Φ6 ×12 mm 的 Zr55Ti5Al10Ni17.5Cu7.5Ag5非晶合金

图1 是 Zr55Ti5Al10Ni17.5Cu7.5Ag5(Φ6 ×12mm)非晶合金的压缩应力-应变曲线及扫描电镜照片，试样在压缩至应变为2.74%时即卸载，以便在整个试样上观察主剪切滑移面和萌生的剪切带 (图1b).由图1可以看出，非晶合金的整体宏观应力-应变曲线表现出理想弹塑性行为，但同时还存在变形高度局部化的剪切带，这说明仅仅采用应力和应变两个参量来描述非晶合金本构行为是不够的，还需要引入其他内部参量.另外，从连续介质力学的观点来看，剪切带实际上是应变软化导致局部化变形的结果.因此非晶合金本构关系应该具有捕捉剪切带的能力.基于描述非晶合金微观变形机制的自由体积理论，本文引入自由体积为内部参量. 自由体积理论［3］如下:

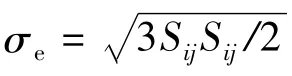
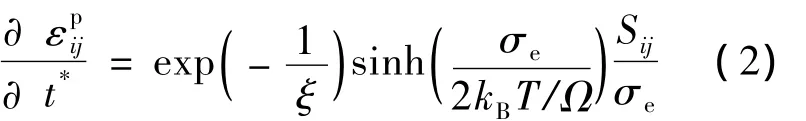
其中ξ=vf/(αv*)为引入的内部参量.自由体积变化演化方程［3］为

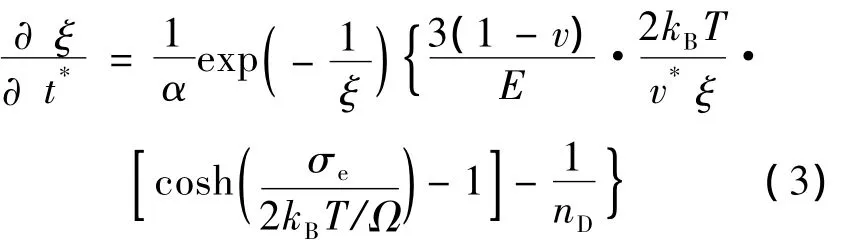
应力与应变关系为

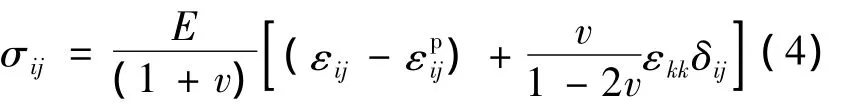
本构关系通过ABAQUS中的UMAT子程序实现.本文旨在定性模拟剪切带，不考虑具体应力大小，取不计量纲的本构参数为:E=170，v=0.36，α =0.105，nD=3，v*/Ω =1，参考应力值2kBT/Ω=1.初始自由体积 ξ(t*=0)作为初始随机材料缺陷的参数赋予材料.

2 计算模型

计算模型几何尺寸、单元划分、边界条件见图2.计算在平面应变下进行，模型划分为5000个CPE4I矩形单元，通过FORTRAN子程序在1～5000(单元的最大数)之间按均匀分布抽取随机数1000次，记下随机数ri，然后对编号为ri的单元赋予随机初始自由体积，

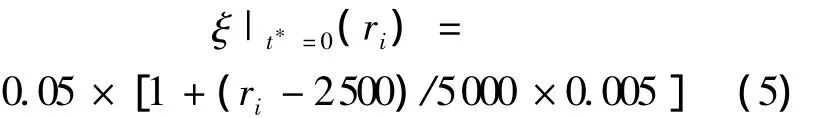
图2 非晶合金压缩计算模型示意图

这样便通过随机选取单元和初始自由体积定义了模型的初始随机材料缺陷，这也符合实验室制备出的非晶合金内自由体积难以确保均匀分布的实际情况.其他单元定义为理想均匀材料，即取ξt*=0=0.05.基于ABAQUS的非晶合金剪切带模拟的整个流程如图3所示.

图3 实现剪切带模拟的流程图

3 模拟结果及分析

3.1 模型宏观载荷-位移曲线

由于计算模型采用的加载方式是位移控制法，事先无法得知载荷信息，只有通过计算结果才能确定载荷与位移间的关系.图4给出了模型整个计算时间内的宏观载荷-位移曲线，因模型所给本构参数为无量纲量，故载荷F的单位任意.由图4可以看出，模型先是线弹性响应，经历一小段非线性阶段后达到载荷峰值，非线性段的出现可能是因为模型内部随机材料缺陷对宏观响应的影响.峰值过后，模型迅速软化，直至破坏失效，这与非晶合金具有应变软化的特征一致.另外，因为本文的研究重点是剪切带的模拟，所以图4未能捕捉到非晶合金完整的载荷-位移响应曲线，这也是图4与实验曲线图1a不完全一致的原因.值得一提的是，对于这类具有应变软化的不稳定材料，采用位移控制法加载一般是无法捕捉到完整的平衡响应历程的，一旦材料进入软化阶段，负刚度出现使得模型变得不稳定［11］，这也是本文只捕捉到剪切带而无法得到真实实验曲线的一个原因.

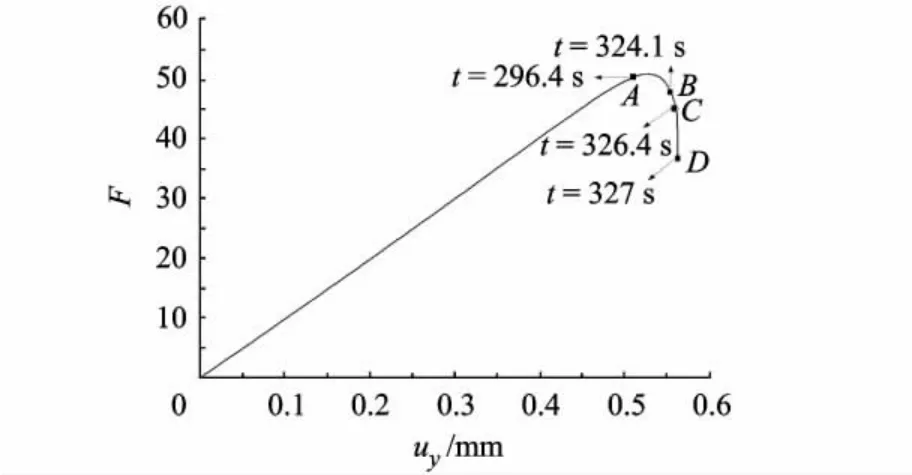
图4 载荷-位移曲线 (F单位任意)

3.2 应变局部化及剪切带形成

图5、图6分别给出了对应于图4曲线上A，B，C，D 4个状态的自由体积ξ和模型轴向应变εy的分布.可以发现，在接近峰值载荷的A点，模型只是在初始随机材料缺陷位置上出现应变局部化，而且应变幅值波动很小，十分接近均匀变形情况 (图6a);自由体积分布也类似于初始状态，自由体积波动仅仅局限在原来施加随机缺陷位置处 (图5a).应变和自由体积的这种分布特点，正好符合加载至A点时材料并未软化的事实.但当加载至超过峰值载荷的B点时，情况与A点截然不同.由图5b可看出，自由体积波动不再局限于初始缺陷位置，一些初始缺陷位置及其周围区域的自由体积呈现出均匀化分布，并且具有较多自由体积的位置有向某些带内集中的趋势，这说明自由体积在某些带内局部增加会使周围松弛而出现均匀分布现象.图6b的应变分布也呈现出类似的情况，应变局部化集中于带内而一些区域出现均匀变形，各条小带成为剪切带成核的可能位置.随着材料进一步软化，当加载至C点时，应变局部化仅出现在两条带内，并且剪切带分别在这两条带内成核、形成并扩展(图6c).同时，其他区域应变局部化消失，这进一步验证了应变局部化集中于带内可松弛周围区域的结论.在C点时，剪切带已经形成，模型就变得非常不稳定了，稍微加载至D点，两条剪切带就迅速扩展直至贯穿整个模型.

3.3 自由体积、应变局部化和剪切带间的关系

对比图5和图6可以看出，自由体积较多的位置几乎和应变局部化的位置重合，说明应变局部化发生在自由体积含量高的地方.仔细分析B，C，D的软化阶段，可以发现，自由体积在某些带内的不断增加造成了应变局部化的出现，比如图5c所标示的MN区域.为了定量分析自由体积与应变软化的关系，以图6d中箭头所示剪切带为例，图7给出了沿此剪切带 (从左上至右下的方向)的自由体积和轴向应变的变化曲线.很明显，在加载点A，自由体积和初始状态几乎一样，应变也接近均匀分布.随着加载进入软化阶段，MN区域的自由体积急剧增大，从B点到D点加载的位移只有0.051 mm，而最大自由体积由0.12增加至0.37(图7a)，最大应变由0.06增加至0.73(图7b).这充分说明了自由体积的增加会导致变形局部化的发生，与描述非晶合金微观变形机制的自由体积理论［3］的结果相符.由以上分析剪切带的形成过程可以看出，剪切带首先是在应变高度局部化的地方成核，然后随着软化过程的进行而迅速形成和扩展.也即表明，应变局部化或局部自由体积增加是剪切带成核的必要条件，而剪切带的形成和进一步扩展则是应变软化不可逆的结果，这同样与自由体积理论［3］预测一致.

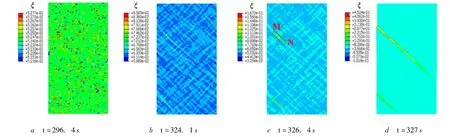
图5 非晶合金剪切带成核、形成和扩展过程中自由体积ξ的变化历程

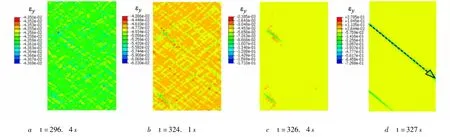
图6 非晶合金剪切带成核、形成和扩展过程中轴向应变εy的变化历程

图7 剪切带内 (沿图6d箭头方向)的变化曲线

4 结论

在本文建立的本构关系框架内，给计算模型赋予以自由体积为参量的初始随机材料缺陷，采用有限元法能模拟出剪切带的成核、形成和扩展等非晶合金剪切带的主要特征，并能捕捉到自由体积在整个加载历程中的变化过程.模拟结果所呈现出的宏观应变软化、应变局部化、自由体积分布和剪切带行为的特点，符合非晶合金自由体积理论预测结果以及实验观察.本文方法模拟非晶合金剪切带是有效可行的.

References)

［1］Greer A L.Metallic glasses ［J］.Science，1995，267(5206):1947－1953

［2］Johnson W L.Bulk glass-forming metallic alloys:science and technology［J］.MRS Bull，1999，24(10):42－56

［3］Spaepen F.A microscopic mechanism for steady state inhomogeneous flow in metallic glasses ［J］.Acta Metall，1977，25(4):407－415

［4］Steif P S，Spaepen F，Hutchinson J W.Strain localization in amorphous metals［J］.Acta Metall，1982，30(2):447 －455

［5］Hays C C，Kim C P，Johnson W L.Microstructure controlled shear band pattern formation and enhanced plasticityof bulk metallic glasses containing in situ formed ductile phase dendrite dispersions［J］.Phys Rev Lett，2000，84(13):2901 －2904

［6］Zhang Z F，Zhang H，Pan X F，et al.Effect of aspect ratio on the compressive deformation and fracture behavior of Zr-based bulk metallic glass ［J］.Philos Mag Lett，2005，85(10):513－521

［7］Liu F X，Liaw P K，Wang G Y，et al.Specimen-geometry effects on mechanical behavior of metallic glasses［J］.Intermetallics，2006，14(8/9):1014 －1018

［8］Anand L，Su C.A theory for amorphous viscoplastic materials undergoing finite deformations，with application to metallic glasses［J］.J Mech Phys Solids，2005，53(6):1362 －1396

［9］Gao Y F.An implicit finite element method for simulating inhomogeneous deformation and shear bands of amorphous alloys based on the free-volume model［J］.Modelling Simul Mater Sci Eng，2006，14(8):1329－1345

［10］Wu W F，Zhang C Y，Zhang Y W，et al.Stress gradient enhanced plasticity in a monolithic bulk metallic glass［J］.Intermetallics，2008，16(10):1190－1198

［11］Dassault Systèmes Simulia Corp.ABAQUS V6.9 User's manual［M］.RI:Dassault Systèmes Simulia Corp，2009