热毛细对流模式转换及温度振荡特征
2012-06-22朱鹏段俐康琦
朱 鹏 段 俐 康 琦
(中国科学院力学研究所国家微重力实验室,北京100190)
空间微重力环境为晶体生长提供了良好条件.人们开展了多次空间晶体生长实验,结果表明虽然微重力环境基本克服了密度分层、浮力对流等对晶体生长的不利影响,但是最终生成的晶体质量不总是尽如人意.其原因在于热毛细对流的不稳定性.在某些情况下晶体熔融体内的对流会发展为非稳态的振荡对流,随之而来的温度脉动使生成的晶体内部出现和地面情况类似的条纹缺陷[1].如何抑制振荡热毛细对流的产生,从而避免条纹缺陷,成为提高空间与地面晶体生长质量和效率亟待解决的问题,有必要对热毛细对流开展深入研究.
文献[2]利用线性稳定性分析了薄层流体热毛细对流的热毛细稳定性,得到2种热毛细对流不稳定性:定常的纵向涡胞排列和非定常的热流体波.之后,关于热毛细对流的理论分析,文献[3]增加考虑了重力的影响,文献[4]考虑了自由面的热耗散,文献[5]考察了三维的对流流动状态.除了理论研究,人们还对热毛细对流进行了不少实验研究.1998年,文献[6]实验研究了矩形液池中液层浮力-热毛细对流的热流体波以及它的各种特性.2001年,文献[7]对不同长高比矩形液池中浮力-热毛细对流的不稳定性进行了实验研究.2007年,文献[8]利用实验和数值模拟的方法研究了薄液层中的热流体波,并发现与液桥中的自由面温度行波具有相似性.
热毛细对流是空间环境中自然对流的主要形式,但是人们对其流动规律,特别是其振荡机理的认识仍然很有限.本文的研究目标是通过实验观测热毛细对流的温度振荡现象和数值模拟微重力条件下的热毛细对流,分析振荡特征和机理.研究内容包括利用热电偶温度测量系统,实时测量流体的温度演变过程.然后改变实验参数,获得各种实验条件下温度振荡的临界条件.另外,利用flow3d数值模拟软件,仿真微重力条件下的热毛细对流的流动.
1 实验模型及方法
本文作者在实验室设计了一个热毛细对流控制系统,图1是该系统的简化图.矩形液池的右壁面是贴有电热膜的6 mm厚的铜块,左壁面是粘有半导体制冷片的同样也是6 mm厚的铜块.半导体制冷片的外面贴有散热片能够加速散热.液池的前后面和底面都是6 mm厚度的K9玻璃.实验中,实验介质采用0.65号和1号硅油.直流电源和2个温控仪能够控制电热膜和半导体制冷片的工作,从而使2个铜片之间产生温差.随着两端温差的增加,液池中硅油液层内的对流就会失稳,出现振荡的现象.
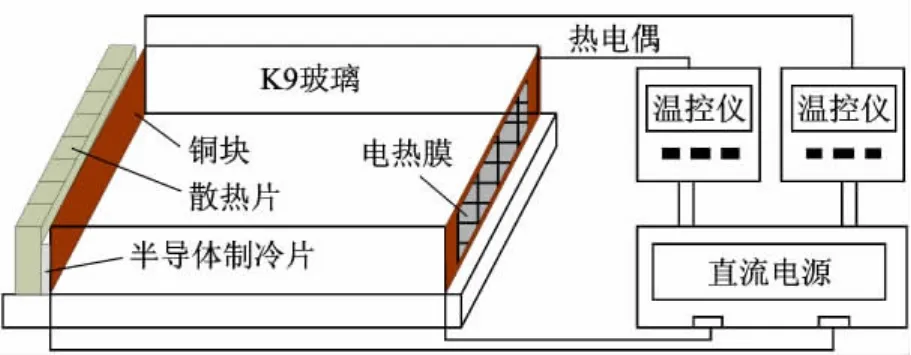
图1 热毛细对流控制系统
为了测量并记录液层中流体温度在一段时间的演变,设计了一个温度测量系统.如图2所示,这个系统主要由T型热电偶、纳伏表和数据采集电脑3部分组成.系统中的传感器是直径为60 μm的T型热电偶.实验中,热电偶先将温度信号转变为能够被纳伏表识别的电压信号,然后根据温度和电动势之间的关系演算出对应的温度值,再实时地记录在电脑中.该系统的分辨率可以达到0.001℃,工作时的采样率是5 Hz.
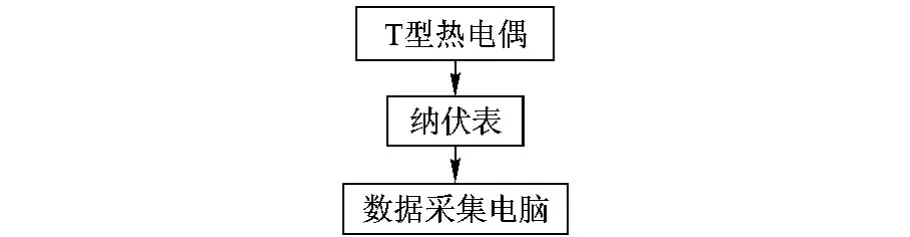
图2 温度测量系统
2 实验结果及分析
对于矩形液池中液层的热毛细对流,当两端温差比较小的时候,流动对应着层流的流动状态,对应的液层中一点的温度是一个确定的数值;随着两端温差的增加,当其超过某一临界值,流体的温度就开始发生明显的振荡;随着温差的进一步增加,温度的振荡会逐渐演变为混沌,而同时流体的流动也会演变到湍流的流动状态.本文实验将主要关注温度发生振荡的临界条件,以及起振之后温度振荡的一些特征.
温度的时间曲线反应了对流的流动模式.图3a给出了两端温差ΔT=12℃时,液层中测量点温度随时间的变化.可见,温度只是在上下±0.01℃的范围内随机地变化,这些只是由于环境扰动和测量仪器导致的噪声所引起的.所以此时应该对应着层流的流动状态,流动还没有发生振荡.在图3b中,两端温差ΔT=15℃,此时测量点的温度在一个平均值附近周期性地来回振荡,振荡的幅度达到±0.05℃.所以此时应该对应了对流第一次模式转变之后的流动状态.图3c中,当液层两端温差达到ΔT=43℃时,流体的温度振荡变得不再规则,振幅达到±1℃.此时,液层的流动已经发展到湍流的流动状态.
图3给出了临界温差前后温度的时间曲线,逐渐缩小范围就可以得到临界温差.在实验中,对0.65号和1号硅油进行了温度振荡的观察,得到了不同液层厚度条件下温度振荡的临界条件,见表1.对于6 mm高的液池,本文只是在一定的液层厚度范围内观察到温度的振荡.当厚度太小,液层内部很难建立比较好的流动;当厚度太大,自由面很接近液池顶部,液体很容易顺着直角和盖子爬出液池.
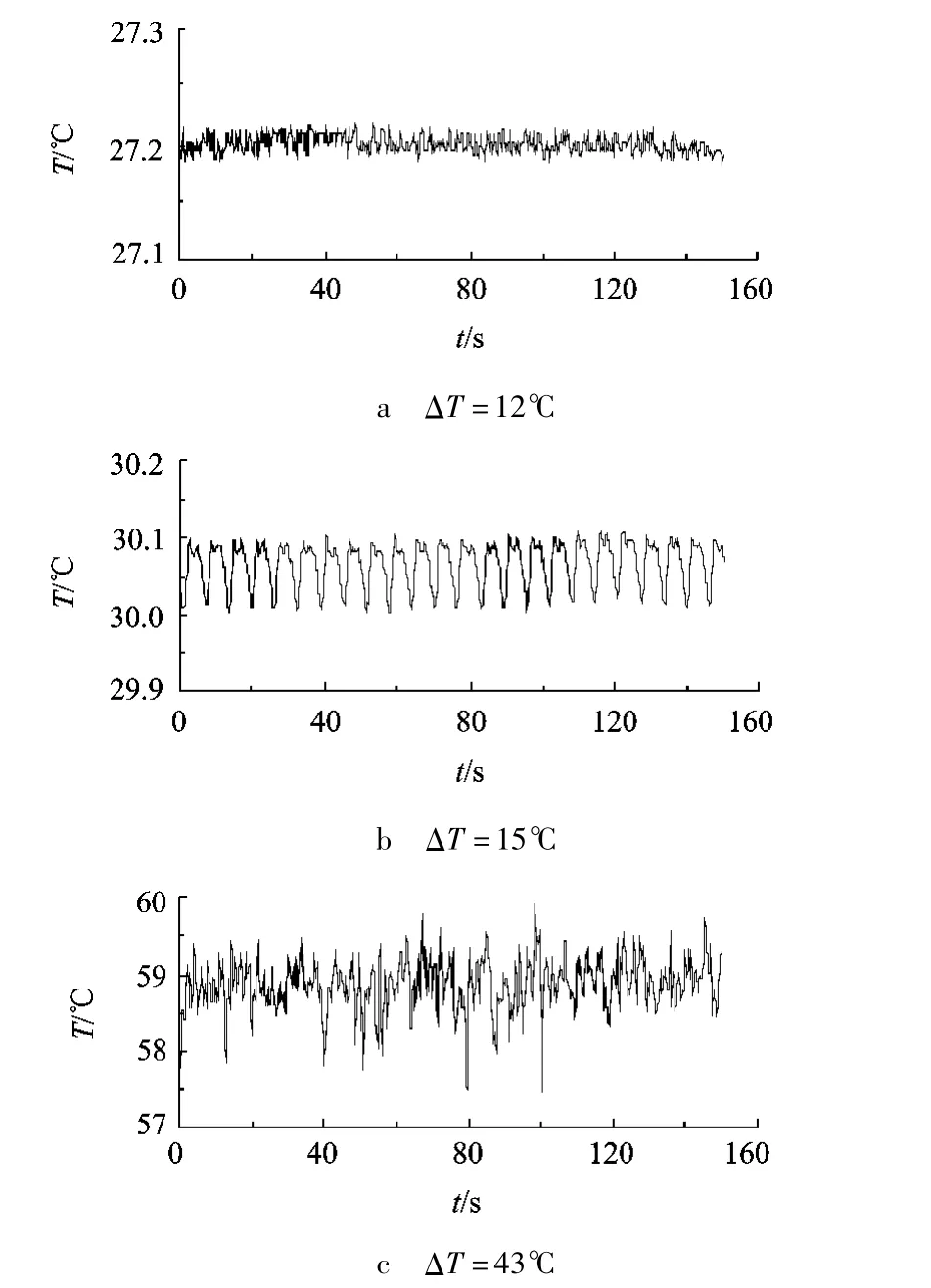
图3 温度曲线
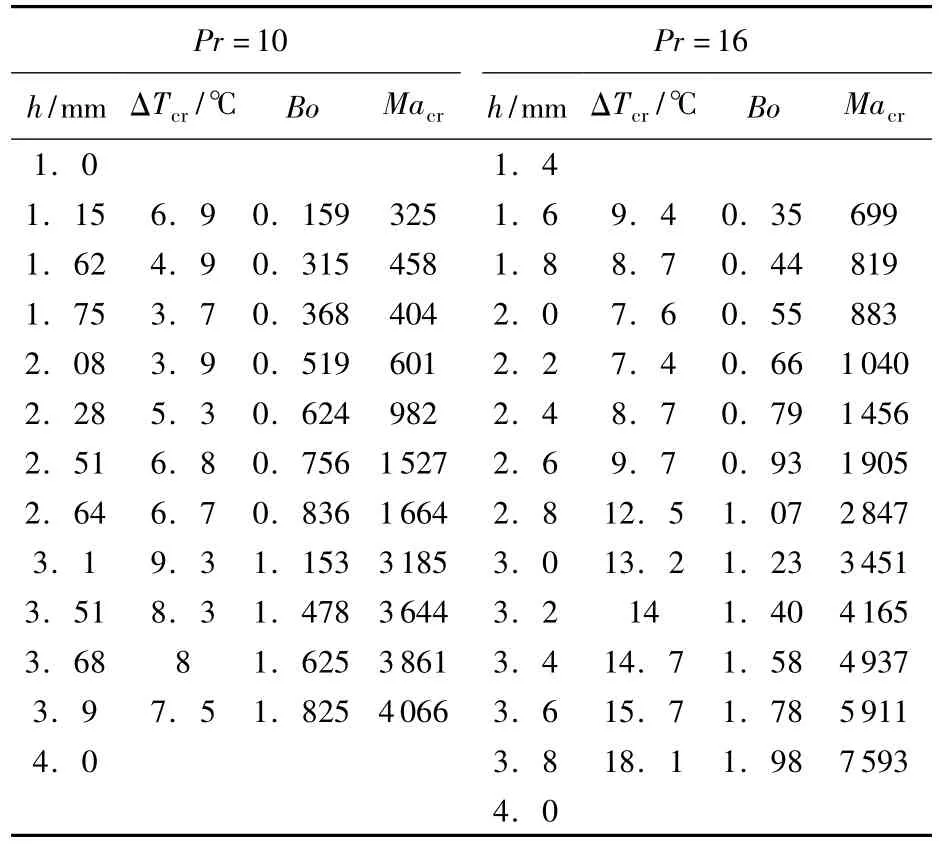
表1 0.65号和1号硅油临界条件
为了对实验结果进行讨论,把实验条件无量纲化.用式 (1)来表征温度振荡的起振,用式(2)来描述重力和热毛细力的相对强弱.
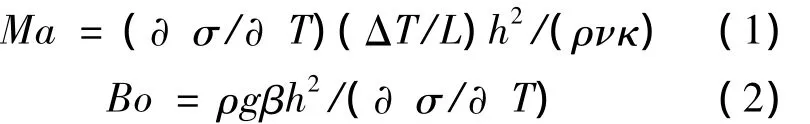
式中,σ为表面张力;T为流体温度;L为液层横向长度;ρ为实验流体密度;ν为实验流体动力粘度;κ为热扩散系数;g为重力加速度;β为热膨胀系数;Bo为Bond数.
图4给出了2种硅油Macr-Bo曲线.可见,对于同一种硅油,Macr随着Bo的增加而变大,说明重力的增强使对流的流动变得更加稳定.对比2种Pr的硅油,当Bo<1.2时,两者的变化曲线基本一致;当Bo>1.2时,对于同样的Bo,高Pr的硅油对应的Macr更大,即高Pr的硅油更加稳定.
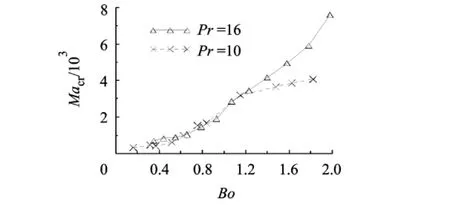
图4 0.65号和1号硅油Macr-Bo关系曲线
在一些数值模拟结果[9]中,包括本文用flow3d的仿真结果,热流体波都是先在某些局部区域起振,然后才扩展到整个流场.为了检验这种现象,实验中用2套设备同时测量并记录了液层中不同位置的温度振荡.由图5可见,随着两端的连续升温,测量点的温度也会增加,随后都会发生温度的振荡.为了更加清楚地观察它们的起振过程,用小波变换的方法从原始信号中提取出温度振荡的信号.从2个测量点的振荡信号可以看到,它们几乎是同时起振.实验中,当任意更换2个测量点的位置,也都是同样的结果.由此可以得到,在实验中,液层中的热毛细对流一旦发生温度的振荡,整个流场范围内几乎同时起振.
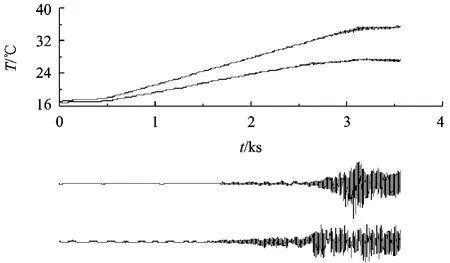
图5 不同位置温度振荡对比
3 数值模拟结果及讨论
为了探讨微重力条件下的热毛细对流,用flow3d软件数值模拟了零重力时相同尺寸液池中热毛细对流的流动状况,发现了一种自由面晃荡的现象.在一开始温差建立的阶段,在自由面,由于水平温度梯度引起的表面张力梯度会驱使自由面的流体从热端流向冷端.由于缺少了重力的下拉作用,流体会明显地在冷端堆积,从而使自由面产生明显的变形.在经历了一段时间充分发展之后,自由面就发生一种晃荡的现象.如图6所示,它给出了横向自由面变形在半个周期内的变化情况.自由面大概以中间的虚线为平衡位置来回地晃荡.本文认为这种晃荡的现象主要是由自由面的变形和液层流场的相互作用导致的.当自由面到最大变形处时,热端液层变薄,流体运动到冷端时的流速变小,流速对应的动压不足以与自由面的张力相平衡,自由面就会趋向平衡位置.随着自由面变形的减小,液层内部的流速又会恢复,直到自由面越过平衡位置到达最小变形处,恢复的流速对应的动压又会使自由面加大变形.如此反复,就会产生这种自由面晃荡的现象.
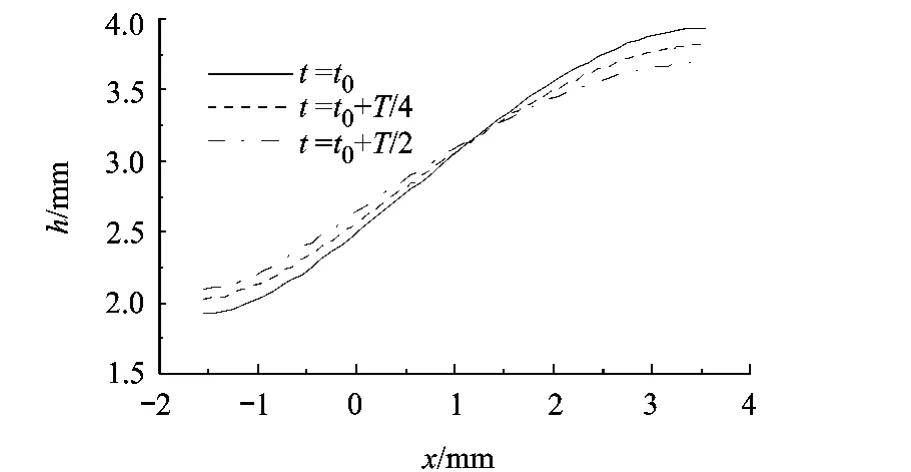
图6 自由面变形
图7是提取出微重力条件下热毛细对流演变过程中冷端接触点位置随时间的变化.可见,对于3 mm厚度的液层,自由面的最大偏移是1.2 mm,晃荡的振幅达到0.2 mm,周期约为6.5 s.图8是相同条件下液层中某一点的温度随时间的变化.同样可见,振荡的周期也约为6.5 s,振幅达到0.18℃.

图7 冷端接触点偏移
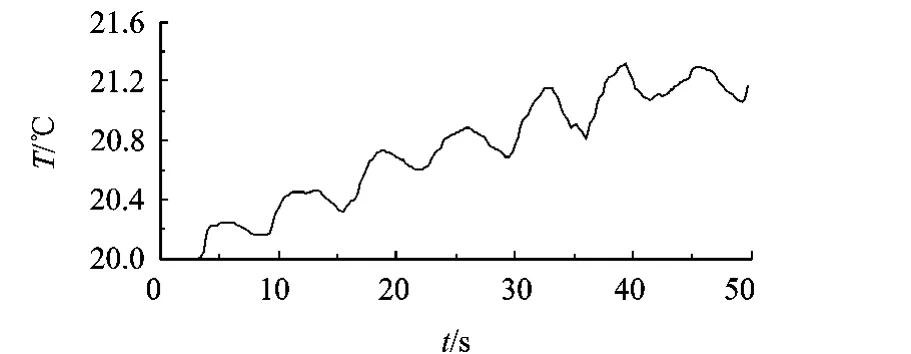
图8 微重力条件下热毛细对流温度振荡
4 结论
本文通过实验和数值模拟的方法研究了矩形液池中由于自由面水平温度梯度导致的热毛细对流.首先定量地测量了各种稳态条件下热毛细对流液层中温度的演变过程,观察到了热毛细对流的温度振荡现象,并且获得了各种实验条件下温度振荡的临界条件,讨论了它与Pr和Bo之间的关系.与很多数值模拟结果不同的是,实验中温度的振荡在整个流场中几乎同时起振.另外,数值模拟了微重力条件下的热毛细对流,发现了一种由自由面变形和液层流场相互作用导致的晃荡的现象.
References)
[1]Jakeman E,Hurle D T J.Thermal oscillations and their effect on solidification processes[J].Review of Physics in Technology,1972,3(1):3-30
[2]Smith M K,Davis S H.Instabilities of dynamic thermocapillary liquid layers part 1:convective instabilities[J].Journal of Fluid Mechanics,1983,132(7):119-144
[3]Parmentier P M,Regnier V C,Lebon G.Buoyant-thermocapillary instabilities in medium-prandtl-number fluid layers subject to a horizontal temperature-gradient[J].International Journal of Heat and Mass Transfer,1993,36(9):2417 -2427
[4]Mercier J F,Normand C.Buoyant-thermocapillary instabilities of differentially heated liquid layers [J].Physics of Fluids,1996,8(6):1433-1445
[5]Kuhlmann H C,Albensoeder S.Three-dimensional flow instabilities in a thermocapillary-driven cavity[J].Physical Review E,2008,77(3):036303
[6]Riley R J,Neitzel G P.Instability of thermocapillary-buoyancy convection in shallow layers part 1:characterization of steady and oscillatory instabilities [J].Journal of Fluid Mechanics,1998,359(3):143-164
[7]Burguete J,Mukolobwiez N,Daviaud F.Buoyant-thermocapillary instabilities in extended liquid layers subjected to a horizontal temperature gradient[J].Physics of Fluids,2001,13(10):2773-2787
[8]Kawamura H,Tagaya E,Hoshino Y.A consideration on the relation between the oscillatory thermocapillary flow in a liquid bridge and the hydrothermal wave in a thin liquid layer [J].International Journal of Heat and Mass Transfer,2007,50(7/8):1263-1268
[9]Tang Z M,Hu W R.The hydrothermal wave of large-Prandtlnumber fluid in a shallow cavity[J].Science in China Series G:Physics,Mechanics & Astronomy,2007,50(6):787-796
