角区三维分离流附着鞍点拓扑结构及其演化

张 华 胡 波

Muhammad Yamin Younis

王 宏

(北京航空航天大学 航空科学与工程学院，北京100191)

角区流动广泛存在于航空、航天以及其他诸多空气动力学和流体力学应用领域.由于角区流动包含了丰富而复杂的三维分离现象，并对飞行器和流体机械的性能产生重要影响，因此引起研究者广泛的关注［1－5］.角区典型流动是来流边界层在突起物产生的逆压梯度作用下分离而形成的空间三维马蹄涡系.在对三维分离流的分析中人们广泛应用“极限流线包络线”分离模式［6］、“摩擦力线收拢渐近线”分离线模式［7］和“开式/闭式”分离模式［8－9］来描述三维分离流动，尽管这几种分离描述之间还存在一定差别，但都反映了人们对常规三维分离现象的基本认识:三维分离是近壁流线汇合时向上抬起而形成空间分离面和三维旋涡的现象.

按照文献 ［7］的三维定常分离概念，分离线是从壁面鞍点出发的一根摩擦力线，且是邻近摩擦力线的收拢渐近线，在空间对称面流动结构则体现为分离半鞍点，该常规分离结构被称为“分离鞍点结构”.然而文献 ［10－12］等对圆柱/平板角区层流马蹄涡的数值模拟却表明，对称面近壁流线并非是从壁面向上抬起，而是经由空间的一个鞍点向壁面附着，即角区平板上游鞍点是一个附着鞍点.

文献［13］曾采用激光片光和常规流动显示方法研究附着鞍点结构，然而其实验方法尚缺乏足够的分辨率.文献 ［14］曾利用粒子图像测速 (PIV，Particle Image Velocimetry)技术从定量的角度初步证实了圆柱/平板角区对称面确实存在壁面附着鞍点结构.然而附着鞍点结构的特性及其与传统分离结构的关系尚未被深入了解.本文利用PIV进一步证实在多种角区模型三维分离流中的确存在着附着鞍点结构，并着重研究其与传统分离鞍点结构之间的关系，以及角区流动结构随雷诺数和模型头部形状演化的规律，最后讨论附着鞍点结构与文献 ［7］中Lighthill三维分离模式的关系.

1 实验设备与技术

实验循环小水槽实验段宽300 mm，高400 mm，长500 mm，实验流速0.01～0.1 m/s.实验模型包括三棱柱、4/1(长轴/短轴比，下同)椭圆柱、2/1椭圆柱、3/2椭圆柱、圆柱、1/2椭圆柱、方柱等7种，模型宽度分别为60，80和100 mm，模型高宽比大于2∶1，实验平板总长500 mm，平板前缘为5/2椭圆，将模型安放在平板上，模型距平板前缘300mm.PIV系统光源为双腔Nd:Yag激光器，激光器功率为200 mJ/脉冲，CCD相机分辨率为1 024像素×1 024像素，数据采集频率30 Hz.示踪粒子为粒径400 nm的Al2O3.纵向拍摄范围为50～100 mm.查询窗口采用32像素×16像素，计算步长32像素×16像素.PIV实验采集系统以及模型在水槽中的布置如图1所示.将模型安装在平板上之前对模型处的边界层速度型进行了PIV测试，结果表明平板边界层与Blasius层流边界层速度型符合良好，边界层厚度和速度误差均小于3%.

2 实验结果与讨论

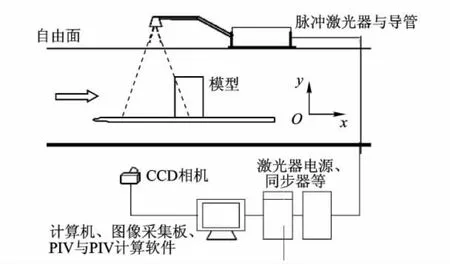
图1 PIV实验系统布置

2.1 角区附着鞍点拓扑结构

实验在7种具有不同前缘钝度的角区模型以及适当的流动条件下均获得了附着鞍点结构(对称面为附着半结点)，图2所示为3种典型角区模型对称面的流动结构.可见对称面上游奇点均为附着奇点而非分离奇点.以单主涡结构为例，从上述实验结果推断的对称面拓扑结构与传统分离拓扑结构对比见图3.

图2 角区附着鞍点结构 (对称面为附着半结点)

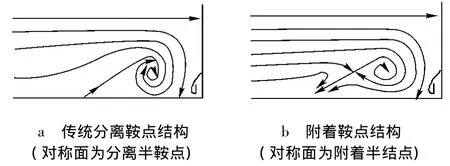
图3 角区对称面两种流动结构的对比

两种拓扑结构的最大区别体现如下:①传统分离结构中上游奇点是分离半鞍点，而新分离结构中上游奇点是附着半结点;②传统分离结构中上游旋涡的涡面来自于壁面半鞍点出发的分离流面，而新分离结构中上游旋涡涡面则来自于空间奇点 (对称面上表现为空间鞍点).尽管两种分离结构在空间上存在上述明显区别，但二者对应的壁面摩擦力线却完全类似，即壁面摩擦力线都向从鞍点出发的某摩擦力线渐近收拢，见图4a与图4b的对比，因此将图4b所示壁面附着鞍点对应的流动称为“附着鞍点结构”.可见附着鞍点结构既不同于经典的分离结构，也不同于经典的附着结构，它是旋涡并非自壁面分离而是自空间鞍点分离的流动结构.虽然文献 ［15］在早期的理论分析中曾指出分离区壁面存在着分离鞍点和附着鞍点两种可能性，却未能给出分离区附着鞍点的实际例子，也没有指出这种附着流动与壁面摩擦力线的关系.文献 ［16］曾引用文献［12］数值模拟的附着鞍点结构，并指出壁面摩擦力线的渐近发散线和渐近收拢线都有可能是附着线，并将第2种情况称为第2类附着线.应该指出上述角区附着鞍点结构是目前所知分离流存在“附着鞍点”的极其罕见的例子，在分离流中还很少碰到，在学者之中也尚未得到广泛接受和深入认识.

进一步的问题是:附着鞍点结构是否是角区唯一存在的流动结构?它与传统分离鞍点结构关系如何?为此进一步开展雷诺数和头部形状等因素对角区流动结构演化影响的PIV实验研究.

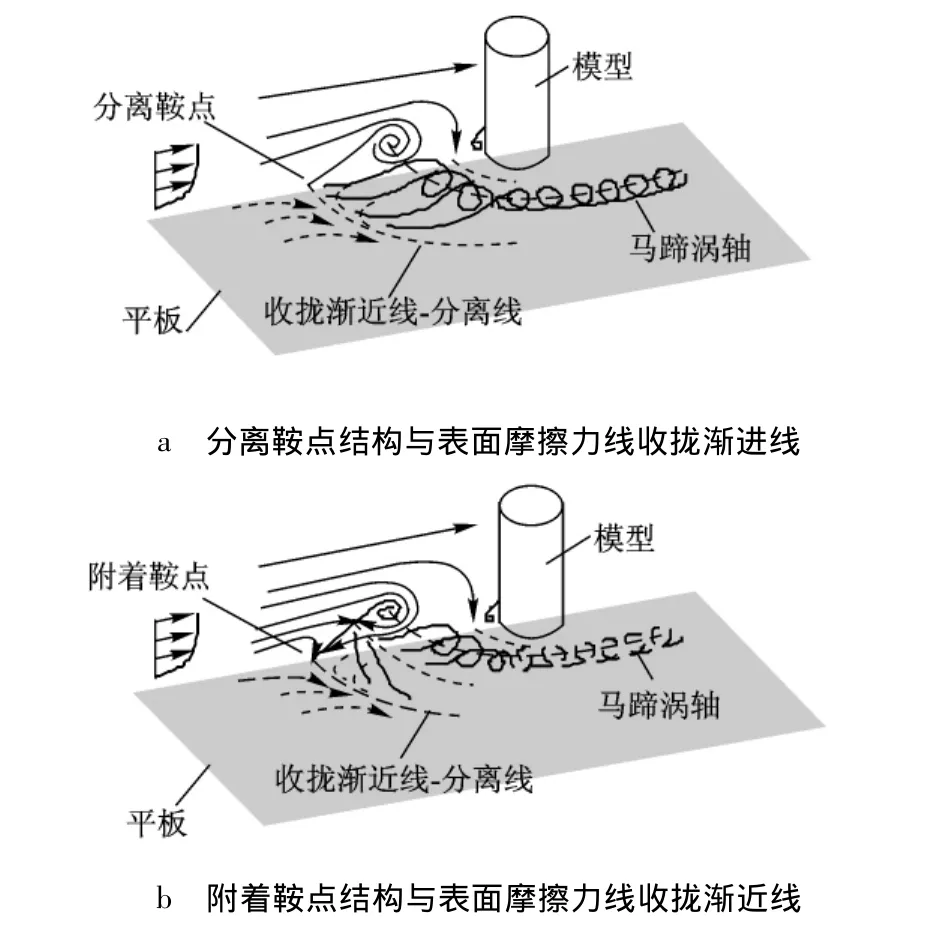
图4 角区两种分离结构与表面摩擦力线的关系

2.2 雷诺数对角区对称面奇点结构演化的影响

由于重点关注对称面上游奇点的性状随雷诺数的演化，为了增加测量分辨率采用CCD相机+微距镜头 (SIGMA-105)重点测量了角区对称面上游奇点局部的流动特性，典型的PIV测量结果如图5所示.可见随雷诺数增加，角区上游奇点附近的性态发生了变化，即从附着半结点演化成了分离半鞍点结构.对称面上附着半结点与传统的分离半鞍点的演化往往发生在较低的临界雷诺数下，例如对3/2椭圆柱/平板角区而言临界雷诺数Recr≈2 000，对方柱/平板角区而言临界雷诺数Recr≈1200，即模型钝度越大则流动结构发生演化的临界雷诺数越低.由于工程应用中的角区雷诺数往往都远大于上述临界雷诺数，因此一般将表现为传统的分离鞍点结构.

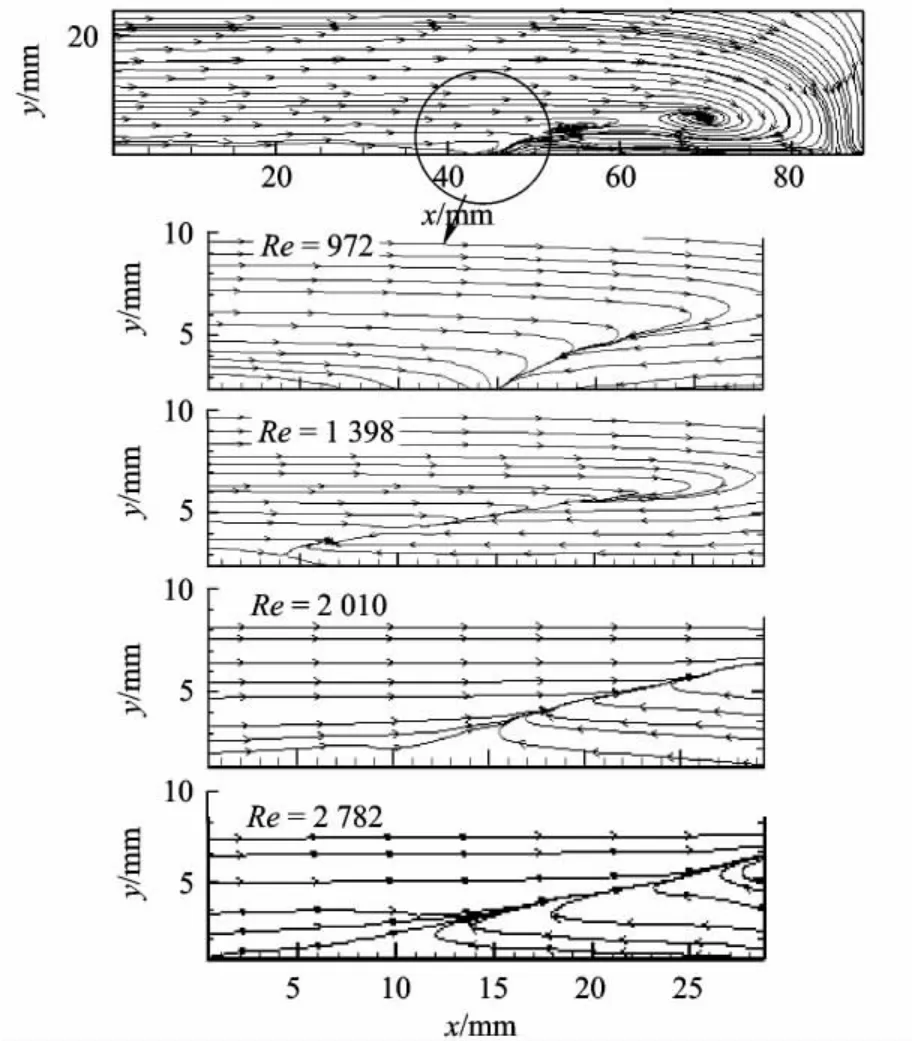
图5 3/2椭圆柱/平板角区对称面奇点结构(局部微距拍摄)随雷诺数的演化

2.3 模型形状对角区对称面奇点结构演化的影响

实验发现在较低的雷诺数下 (例如Re=1100)，所有不同钝度的模型与平板形成的角区均体现为附着半结点结构，当雷诺数增加时，对称面流动结构将会随模型钝度增加而演化，图6给出了典型雷诺数Re=1400时不同模型钝度对角区对称面奇点结构演化的影响.实验在保持水泵一定转速条件下进行，由于模型形状不同造成一定水泵转速下流动损失不同，因此对应实际雷诺数有些许不同.图6中发生流动结构转化的临界模型 (名义Re=1 400)钝度较大，介于1/2椭圆柱和方柱之间.实验发现当雷诺数增加时(Re=2800)，流动结构发生转化的临界模型钝度变小 (介于三棱柱和3/2椭圆柱之间).

上述结果整理为如图7所示的角区流动结构演化临界曲线.给定平板长度 (300 mm)，在一定模型钝度下，随雷诺数增大，角区流动将从附着鞍点结构演化为传统的分离鞍点结构;在一定雷诺数下，随着模型钝度增大则角区流动将从附着鞍点结构演化为传统的分离鞍点结构

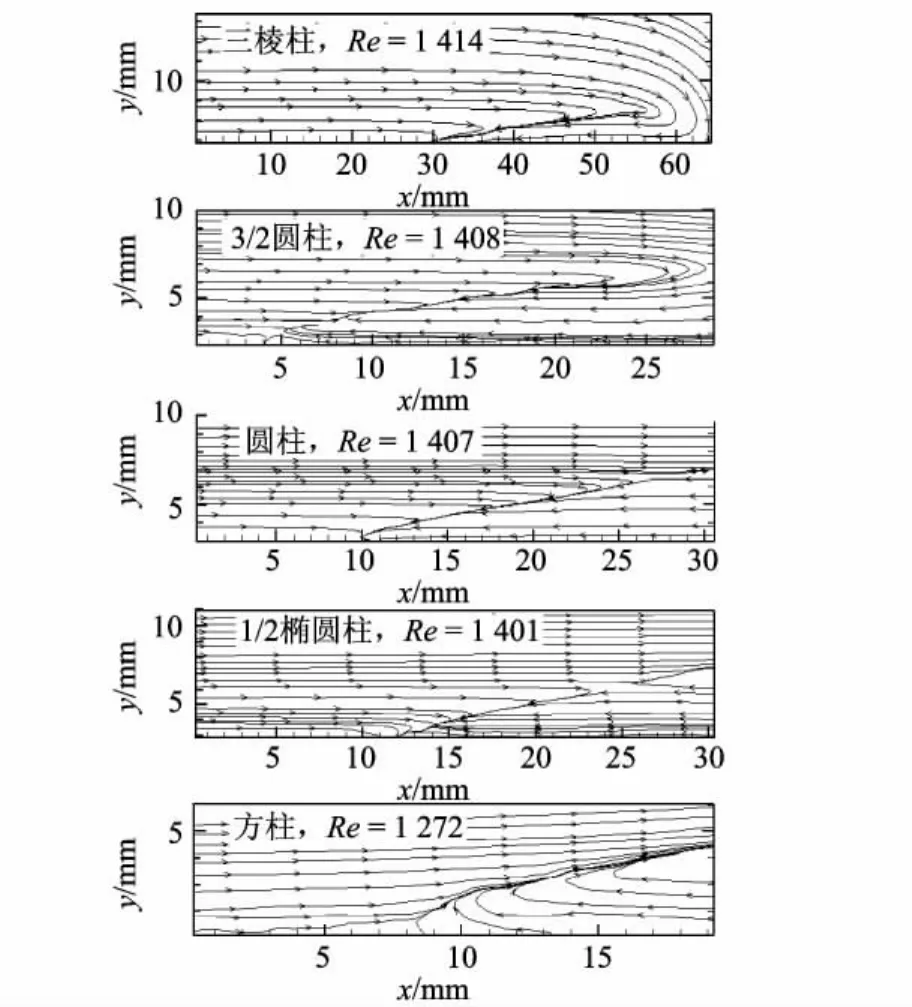
图6 模型钝度对角区对称面奇点结构(局部微距拍摄)演化的影响(名义Re=1400)

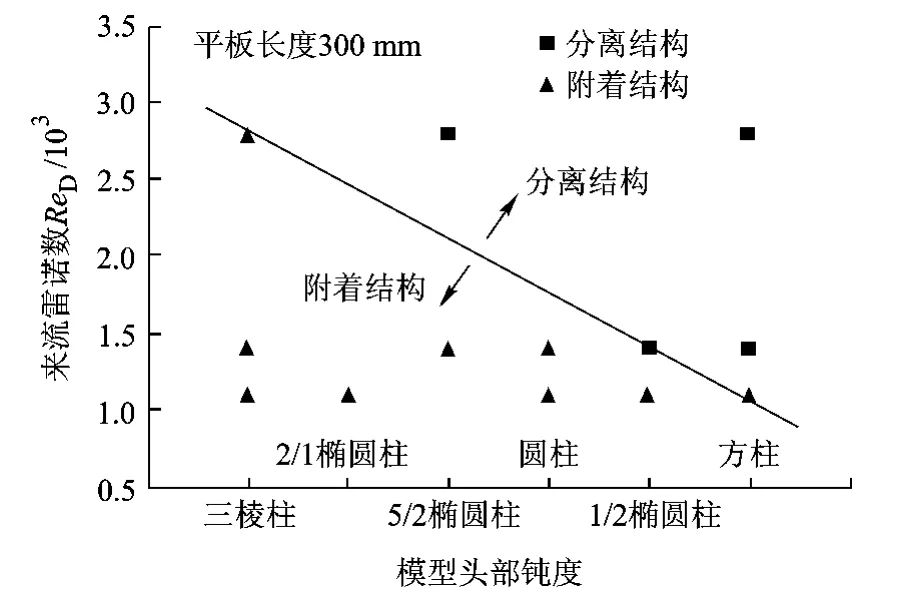
图7 角区附着鞍点结构与分离鞍点结构的演化边界

2.4 附着鞍点结构与 Lighthill［7］分离模式的关系

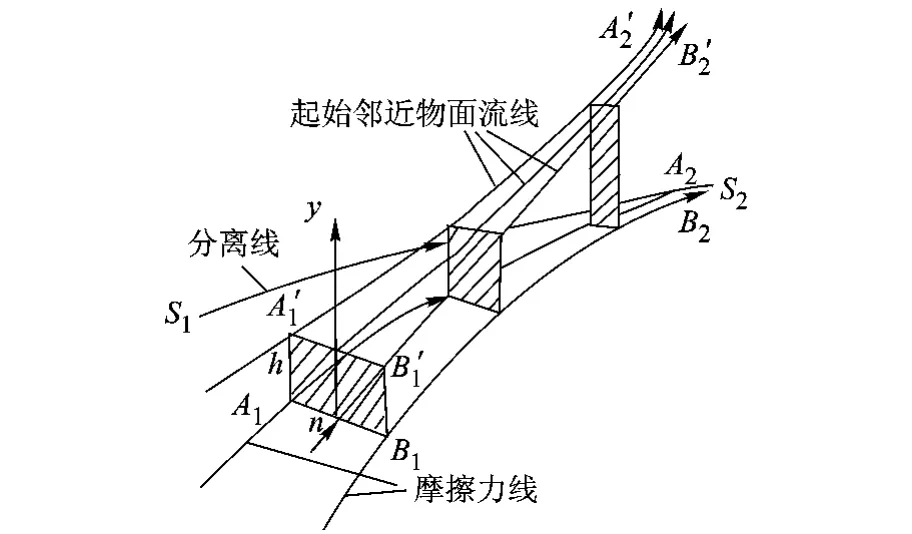
图8 Lighthill［7，17］三维定常分离流动图画

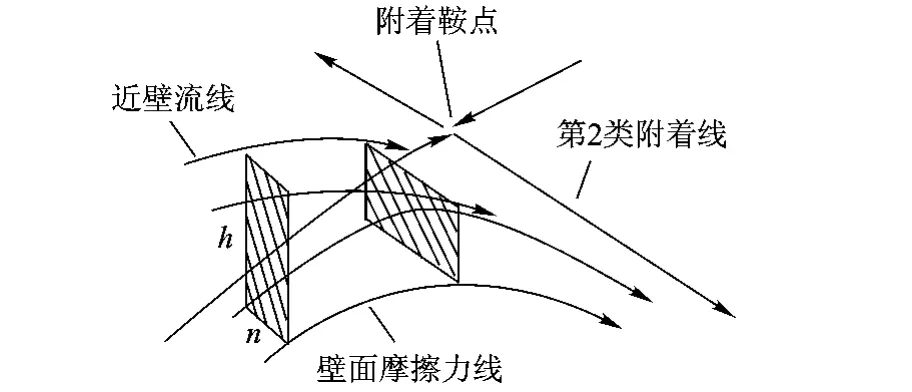
图9 近壁流线接近附着鞍点时可能的流动状态

图10 附着鞍点发出的摩擦力线附近可能的流动状态

上述第2种情况在工程中也有类似的例子，例如在水槽收缩段中，相邻流线逐步收拢，但是水面流线并未因此抬升.在本文实验中由于雷诺数和模型头部形状都将影响角区逆压梯度的大小、分布、涡结构的拉伸和局部曲率，从而影响了角区近壁流线附近相邻流管宽度n和壁面摩擦应力τw相对变化速率，从而使分离涡结构随着雷诺数和模型头部形状变化而发生演化.根据以上讨论，可知文献 ［7］中Lighthill三维分离模式既适用于传统的分离鞍点结构分析，也适用于面附着鞍点结构分析.

3 结论

(1)PIV实验证实了在一定边界层和雷诺数条件下多种形状模型与平板形成的角区均存在有别于传统分离结构的壁面附着鞍点结构:对称面近壁流线并非从壁面向上抬起而从壁面分离，而是经由一个空间鞍点向壁面附着.

(2)角区对称面的奇点结构存在着一定的演化规律，影响参数包括雷诺数和模型头部钝度等.在一定的边界层和模型条件下若雷诺数越大则流动将从附着半结点演化为传统的分离半鞍点结构.在一定的边界层和雷诺数条件下，随着模型前缘钝度逐步加大，流动将从附着半结点结构逐步过渡为传统的分离半鞍点结构.

(3)文献 ［7］中的Lighthill三维分离模式可以适当推广用于分析新的附着鞍点结构.

References)

［1］Simpson R L.Junction flows［J］.Annual Review of Fluid Mechanics，2001，33(1):415－443

［2］Khan M J，Ahmed A.Topological model of flow regimes in the plane of symmetry of a surface-mounted obstacle［J］.Physics of Fluids，2005，17(4):045101－045101-8

［3］Khan M J.Dynamics of the junction vortex［J］.AIAA Journal，1995，33(7):113 －122

［4］Seal C V，Smith C R，Rockwell D.Dynamics of the vorticity distribution in endwall junctions ［J］.AIAA Journal，1997，35(6):1041－1047

［5］Zhang Hua，Lü Zhiyong.The vortex structure in swept wing/body interactions［C］//Proceedings of the 6th Asian Symposium on Visualization.Pusan:［s.n.］，2001:434 －436

［6］Maskell E C.Flow separation in three dimension［R］.RAE Aero Rept 2565，1955

［7］Lighthill M J.laminar boundary layers［M］.Oxford University Press，1963:5－88

［8］Wang K C.Separation patterns of boundary layer over an inclined body of revolution ［ J］.AIAA Journal，1972，10(8):1044－1050

［9］Wang K C.Separation of three-dimensional flow ［J］.MML，1976，18(8):76－54

［10］Visbal M R.Structure of laminar juncture flows［J］.AIAA Journal，1991，29(8):1273 －1282

［11］Chen C L，Hung C M.Numerical study of juncture flows［J］.AIAA Journal，1992，29(18):7－30

［12］Hung C M ，Sung C H ，Chen C L.Computation of saddle point of attachment［J］.AIAA Journal，1992，30(6):6－30

［13］Coon M D，Tobak M.Experimental study of saddle point of attachment in laminar junction flow ［ J］.AIAA Journal，1995，33(12):88－92

［14］张华，吕志咏.应用PIV研究角区三维分离的附着奇点结构［J］.空气动力学学报，2007，25(增刊):37－42

Zhang Hua，Lü Zhiyong.The investigation of saddle point of 3-D separation in juncture flow by PIV ［J］.Acta Aerodynamis Sinica，2007，25(Supplement):37－42(in Chinese)

［15］Perry A E ，Fairlie B W.Critical points in flow patterns［J］.Advances in Geophysics，1974，18(B):299 －315

［16］张涵信.分离流与漩涡运动的结构与分析 ［M］.北京:国防工业出版社，2005:5－67

Zhang Hanxin.Structure analysis of separated flows and vortex motion［M］.Beijing:National Defense Industry Press，2005:5－67(in Chinese)

［17］Tobak M，Peake D J.Topology of three-dimensional and three-dimensional separated flows［R］.NASA-TM-81294，1981