双尾撑布局弹性飞机配平诱导阻力分析与优化

王立波 杨 超 吴志刚

(北京航空航天大学 航空科学与工程学院，北京100191)

双尾撑布局被广泛应用于现代无人机领域，如美国的“影子”，以色列的“苍鹭”等.这类无人机一般采用大展弦比机翼，载重量较大，用于完成长航程或长航时的战术/科研任务，阻力特性是其飞行性能的一项重要指标.而增升减阻一直以来都是飞机设计师们一项重要的研究内容.

目前在诱阻和型阻减缓方面采取的措施包括:①通过机翼展向几何/气动弯扭优化设计控制环量分布形式，进而减小刚性机翼的诱阻［1］;②通过机翼前后缘控制面的优化排布和协调偏转，进而减小机翼诱阻和型阻［2－3］;③采用翼梢小翼并优化翼面+翼尖的几何外形来减小机翼的诱阻和型阻［4］;④综合采取上述若干种措施来减小诱阻和型阻［5］.文献调研结果显示相关研究工作以机翼诱阻或型阻等单项阻力的优化为多，且在分析与优化过程中较少计及结构弹性的影响.

首先，飞机阻力是一项综合参数，只考虑某阻力成分或某部件阻力最优，有可能造成其他阻力成分增加，如单独考虑机翼诱导阻力最小时，平尾诱导阻力并不一定达到最小状态，又如舵面偏转会引起型阻变化，进而影响全机总阻力.其次，现代飞机结构柔性较为显著，气动弹性效应愈加明显，结构弹性对全机配平参数及阻力特性有着不可忽略的影响.因此有必要对弹性飞机配平状态下的多项阻力特性进行综合分析，并通过适当的方法进行优化与减阻设计.

本文主要以某双尾撑布局无人机为对象，研究结构弹性对配平状态各项阻力特性的影响.选定某飞行速度下定直平飞的配平状态作为优化的基准，通过机翼几何扭转角的合理配置，进行全机诱导阻力优化研究，并在其余速度点处加以校核，评估优化工作对其他阻力成分的影响.

1 理论基础

1.1 弹性飞机配平方程

本文选取地轴系OXYZ［6］和弹性飞机的平均体轴系oxyz［7］作为参考坐标系.地轴系OXYZ为惯性轴系，平均体轴系oxyz的原点o与弹性飞机的瞬时质心重合，x轴沿机身轴线向后，y轴垂直于纵向对称面向右，z轴由右手定则确定.

对弹性飞机结构作有限元离散，并设平均体轴系oxyz相对于地轴系OXYZ运动的角速度矢量为ω，速度矢量为V，结点弹性变形向量为u，那么系统的 Lagrange函数［8］为

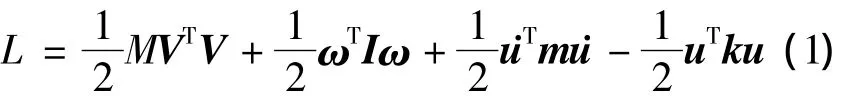
其中，M为弹性飞机的总质量;I为弹性飞机的惯量矩阵，若弹性变形较小，可认为I是常值;m，k分别为弹性体有限元结构的总体质量矩阵和总体刚度矩阵.

认为弹性飞机结构变形较小，结构变形可用前若干阶自由振动模态矩阵Φe和模态广义坐标向量qe的乘积近似表示，即

根据Hamilton原理［8］得到平均体轴系下弹性体Lagrange运动方程

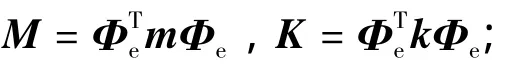
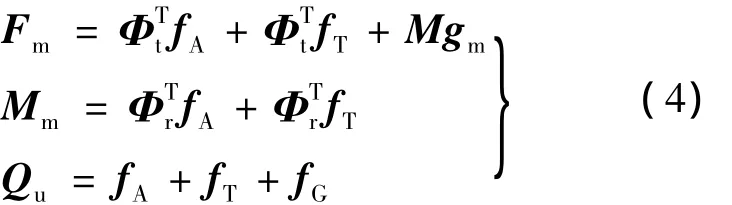
其中，gm为平均体轴系下重力加速度矢量;Φt和Φr分别为弹性飞机刚体平动与转动的模态矩阵.

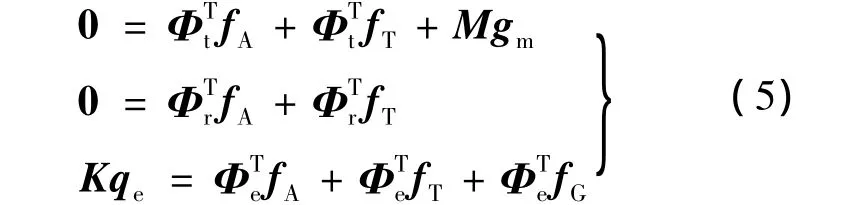
1.2 气动力求解

气动力采用定常涡格法［9］求解，气动力求解坐标系的x轴沿来流方向，y轴水平向右，z轴由右手定则确定.将机翼、尾翼等气动面离散成nv个平面涡格，涡格1/4弦线处布置马蹄涡，自由涡沿顺气流方向，涡格1/4弦线中点为力作用点，涡格3/4弦线的中点为控制点.根据Kutta－Jukovski理论［9］气动网格力作用点处的线性气动力为

其中，qD为飞行动压;AГ为描述附着涡长度与方向的系数矩阵;AAIC为法向诱导速度矩阵;Aδ0为涡格初始偏角向量;q为配平矢量，包括全机攻角、控制面偏角、几何扭角设计参数等控制量，及模态坐标等;Aq为配平矢量对应的系数矩阵.

令结构结点与气动网格结点之间的位移插值矩阵为G，则结构结点处的气动力结点载荷为

1.3 配平阻力计算

本文所定义的配平阻力包括全机零升阻力CD0、配平时舵面偏转引起的型阻CDp和配平状态的全机诱阻CDi三部分.

给定飞行速度下，全机零升阻力和舵面偏转引起的型阻可用文献［10］提供的经验公式求得

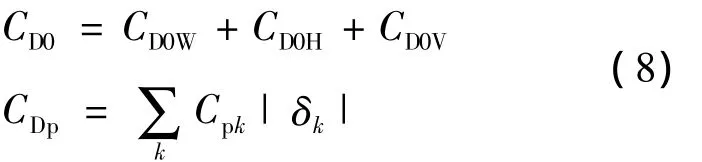
其中，CD0W为机翼零升阻力;CD0H为平尾零升阻力;CD0V为垂尾零升阻力;δk为第k个舵面的偏转角;Cpk为其比例系数.

配平状态的全机诱导阻力基于定常涡格法结合Trefftz平面理论［9］求得.所有涡格控制点在Trefftz平面上投影处的诱导速度可表示为

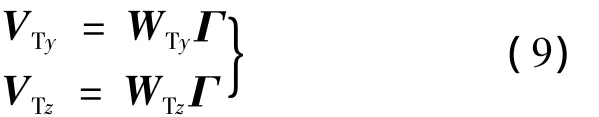
其中，VTy，VTz分别为y和z方向的诱导速度向量;WTy，WTz分别为y和z方向诱导速度影响系数矩阵;Г为涡格马蹄涡的涡强列向量.

根据Trefftz理论和Munk理论［9］得各涡格产生的诱阻列向量为

其中，VTyi，VTzi为Trefftz平面上第i个涡格控制点投影处的诱导速度;lyi，lzi为Trefftz平面上第i个涡格附着涡的长度分量;Гi为第i个涡格的涡强.

根据式 (9)可得

其中行向量⎿ WTy」i，⎿ WTz」i分别表示矩阵 WTy和WTz的第i行.弹性飞机所产生的总诱导阻力为

则全机诱导阻力系数为

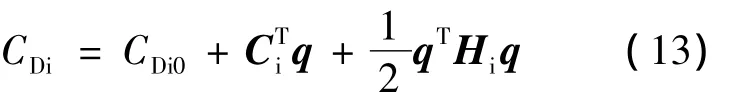
其中各系数项为 (S为机翼参考面积):

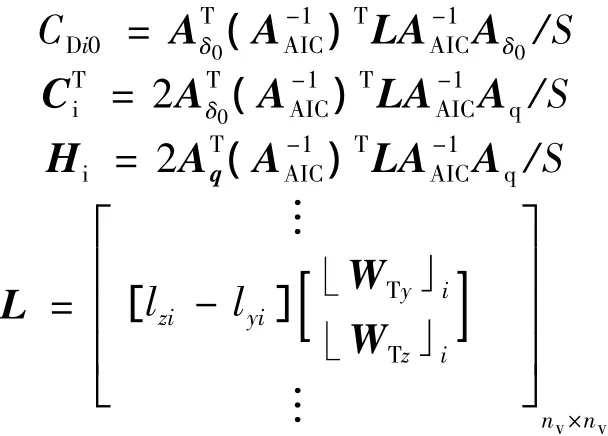
配平状态下全机阻力系数可表示为

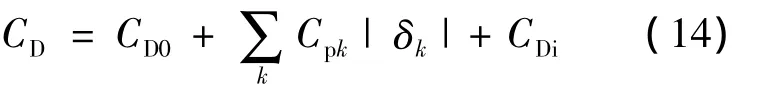
1.4 全机诱导阻力最小的优化问题描述

令弹性飞机纵向配平参数为全机攻角α，升降舵偏角δe，并将机翼几何扭转角在半展长范围内沿展向的分布情况用n段折线表示，共n+1个控制剖面，第i个控制剖面处几何扭转角为δi， 则有

日常要加强饲养管理，科学配制日粮，确保日粮中各个营养元素配比科学，逐渐改变单一饲喂饲料的饲养模式，增强牛体质，及时发现患病牛，采取措施进行对症治疗。另外，为牛群提供充足的清洁饮用水，在冬春季节应该注意增添容易消化的青绿多汁饲料，或投喂青干草，牛群禁食发霉变质的饲料。同时还要确保牛舍布局合理，强化牛舍通风换气，做好牛舍环境卫生，定期消毒，确保圈舍清洁干燥卫生。在选用上述中药进行治疗时一定要耐心，对于病情较为严重的患病牛可能治疗周期较长，多数病例在治疗时由于中药剂量较大，使用次数较多，会出现腹泻症状，这是患病牛胃部内容物排出过程，禁止使用止泻剂，待内容物排干净后，患病牛腹泻症状就会停止。

代入式 (13)即可得到具体形式的全机诱导阻力系数表达式，为二次实函数.

本文在给定飞行速度和配平攻角的情况下进行全机诱导阻力优化和全机配平阻力分析.优化的目标函数是全机诱导阻力系数，设计变量为升降舵配平偏角和机翼展向的n+1个控制剖面处的几何扭转角.约束条件为:满足全机纵向平衡方程式(5)，且机翼几何扭转角变化趋势和升降舵配平偏角均在可行范围内.优化问题表述如下:

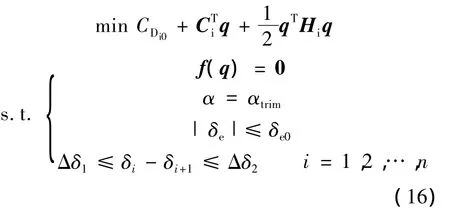
其中，f(q)=0表示弹性飞机纵向平衡方程式(5);αtrim表示优化基准状态的全机攻角;δe0表示升降舵偏转角范围;Δδ1，Δδ2表示机翼两个相邻控制剖面之间相对扭转角范围.式 (16)是二次规划问题，本文采用起作用集方法［11］进行求解.

2 算例模型

本文以某低速载重无人机为例进行具体计算与分析.该飞机为双尾撑布局，大展弦比复合材料平直机翼，机翼内段为矩形，外段为梯形，展长5.4m，展弦比 13.05，翼型为 S1223，面积2.235m2;矩形平尾展长2m，弦长0.24m，翼型为NACA0006，平尾后缘设置全展长升降舵，弦长为当地弦长的33%，全机总重18.56kg.

只考虑纵向配平情况，故建立半翼展模型，结构有限元模型如图1所示，取前25阶弹性振动模态进行配平计算.机翼和平尾的气动力网格划分见图2，忽略机身和尾撑的气动力，在阻力计算中机身、短舱、尾撑均只考虑其零升阻力.

图2 算例双尾撑飞机气动力模型 (半模)

图1 算例双尾撑飞机结构有限元模型 (半模)

3 算例计算结果与分析

3.1 尾撑刚度对全机配平阻力的影响

相关研究表明双尾撑布局飞机的尾撑纵向弯曲刚度对配平攻角、升降舵偏角、平尾升降舵操纵效率等参数均有显著影响［12］.本文选取尾撑段的整体刚度这一关键参数作为研究对象，考虑该飞机在海平面高度定直平飞时尾撑纵向弯曲刚度 (以下简称尾撑刚度)变化对全机配平攻角、全机阻力系数、诱导阻力系数、舵面配平型阻系数，以及机翼和平尾各自诱导阻力等参数的影响.以尾撑初始纵向弯曲刚度为基准，定为EI，分析尾撑刚度分别为0.25EI，0.5EI，EI，2.5EI，5EI及刚性情况时，不同飞行速度情况的计算结果如图3～图7所示.需要说明的是尾撑刚度为0.25EI和0.5EI、飞行速度较大时升降舵配平偏角过大，线性气动力方法可能不再适用，因此上述两个刚度情况的曲线未列出所有速度点，但不会影响变化趋势的分析与判别.

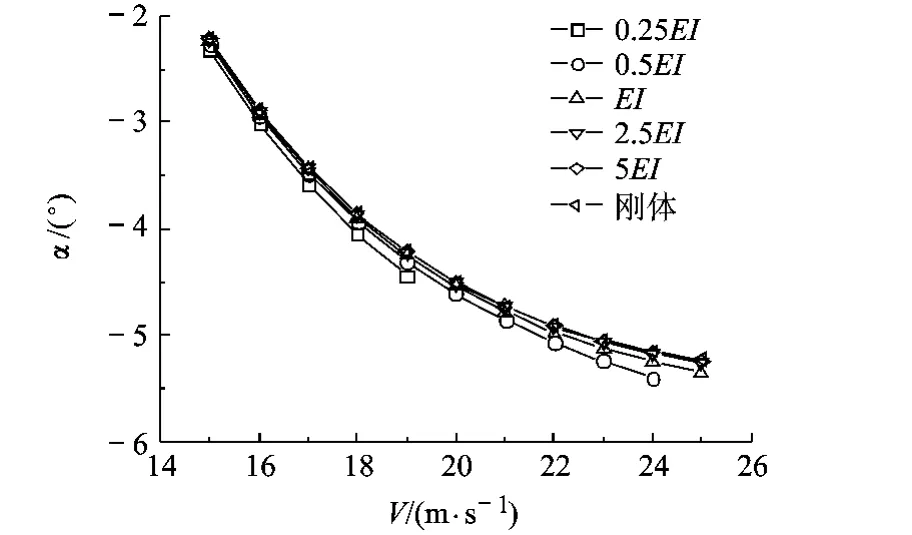
图3 全机配平攻角随飞行速度的变化

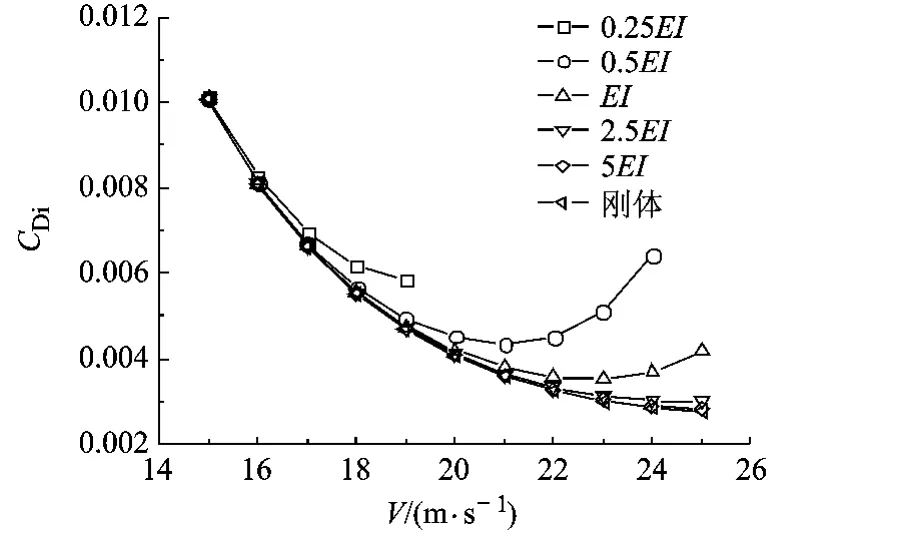
图4 全机诱导阻力系数随飞行速度的变化

图5 平尾诱导阻力占全机诱导阻力百分比随飞行速度的变化

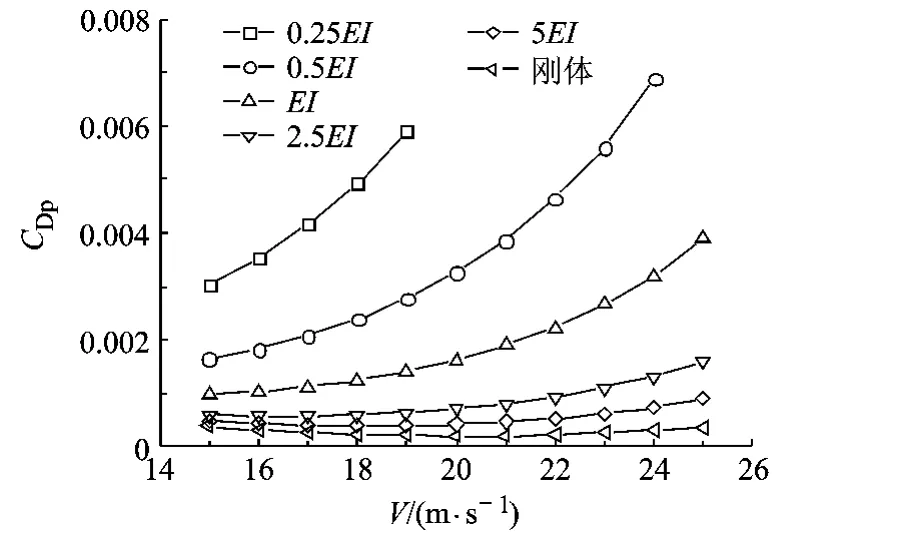
图6 升降舵配平型阻系数随飞行速度的变化

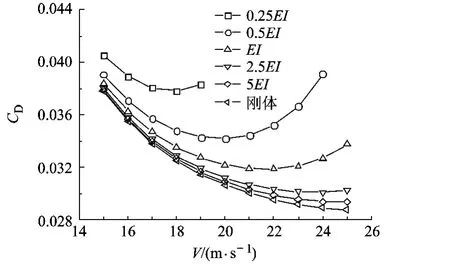
图7 全机阻力系数随飞行速度的变化

图3所示结果表明尾撑刚度变化会对全机配平攻角产生一定程度的影响，图中配平攻角为负值与S1223翼型的弯度较大、零升攻角为负有关.由图4可知，相同飞行速度下，尾撑刚度越大则全机诱导阻力越小.对于某一尾撑刚度情况，其刚度值较大 (为2.5EI，5EI和刚性情况)时，飞机的诱导阻力系数随飞行速度的增加而减小，这与刚体飞机的结论一致，即飞行速度较低时，由于升力系数较大，诱导阻力在平飞阻力中所占比重较大，随着飞行速度的增加，升力系数逐渐减小，诱导阻力也逐渐减小.但尾撑刚度较小 (为0.25EI，0.5EI和 EI)时，飞机诱导阻力系数先随飞行速度的增加而减小，当飞行速度增加到某临界值后，诱导阻力系数反而随飞行速度的增加而增加，而且尾撑刚度越小，该临界速度越低，这一趋势可结合图5的平尾诱导阻力占全机诱导阻力百分比曲线进行分析.图5显示全机诱导阻力中平尾的贡献量随飞行速度的增加而增大，且相同飞行速度下，尾撑刚度越小，平尾产生的诱导阻力越大.这是由于飞行动压增加，受尾撑结构弹性的影响升降舵操纵效率会降低，且尾撑刚度越小升降舵操纵效率降低就越快，需要增大升降舵偏角以达到俯仰平衡.与此同时飞行动压增加，机翼产生更大的低头力矩，平尾需要产生更大的负升力来配平，使得平尾的诱导阻力快速增加，进而造成尾撑刚度较小时全机诱导阻力系数随飞行速度增加先减小后增加的情况.

同样尾撑刚度较小时，升降舵操纵效率低，故配平所需偏角随飞行速度的增加而快速增加，导致配平型阻系数随之增加.而尾撑刚度较大时，升降舵操纵效率较高，配平型阻系数随飞行速度的变化不太明显，具体情况见图6.

3.2 诱导阻力优化与全机配平阻力分析

选取尾撑刚度为EI、飞行速度为20 m/s时的配平状态作优化计算的基准状态 (Base)，并将右半机翼沿展向均匀分为30段，共31个几何扭转角控制剖面进行全机诱导阻力优化.

首先，给定配平攻角αtrim=－4.54°与升降舵偏角δe≤30°，对几何扭转角约束条件 (见表1)作变参优化分析，研究约束条件对优化结果的影响.

表1 各优化状态采用的扭转角约束

不同优化状态下求解得到的配平与阻力特性计算结果如表2所示，图8与图9则给出了各优化状态下扭转角与全机展向升力分布的具体情况.当扭转角的约束限制较弱 (如Opt1)时能获得更好的阻力减缓效果，但会造成机翼局部区域几何扭转角的剧烈变化，对设计和制造不利;而扭转角限制较强 (如Opt3)时，虽便于制造，但会在一定程度上限制诱阻优化的效果.

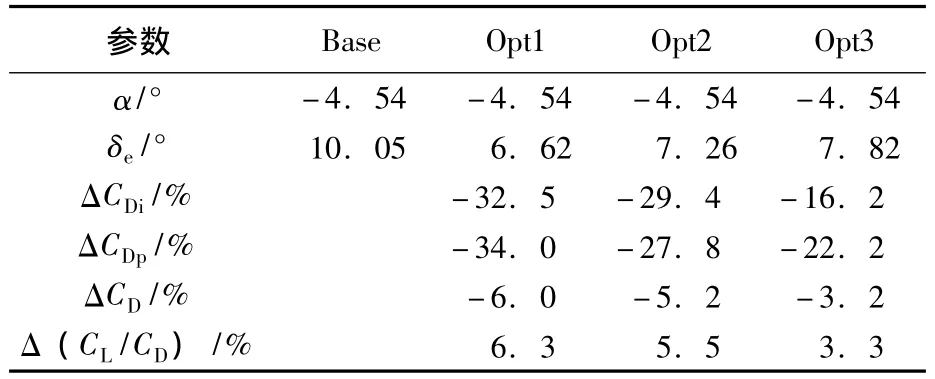
表2 各优化状态纵向配平与阻力特性计算结果

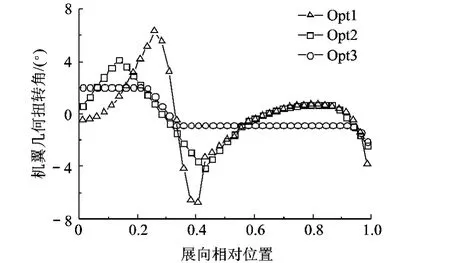
图8 优化得到的机翼扭转角沿展向分布

据表2可知，通过机翼几何扭转角的合理优化可以减小全机诱导阻力约30%.与此同时通过机翼几何扭转角的优化，减小了翼尖的迎角，很大程度上降低了机翼的低头力矩，减小了升降舵配平舵偏和配平型阻，使全机升阻比提高约5%.对比分析图9中优化前后全机展向升力分布形式与标准的椭圆分布可知，优化工作主要通过增加平尾翼展范围 (展向相对位置小于0.40)内的机翼迎角，来抵消平尾产生的负升力，并减小外翼段的攻角，使得全机展向升力分布更加接近于标准的椭圆分布，进而减小全机的诱导阻力.

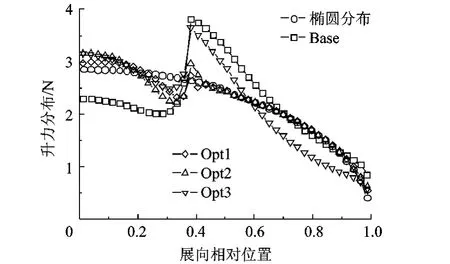
图9 优化前后全机沿展向升力分布形式

根据以上变参分析，选取机翼扭转角约束条件为－1.0°≤δi－δi+1≤1.0°，分别对飞行速度为20 m/s时刚体和弹性双尾撑飞机的全机诱导阻力进行优化，并将优化结果代入其余速度点作配平阻力特性校核分析.优化得到弹性和刚体情况机翼扭转角分布如图10所示，两种情况下机翼扭转角在数值上有一定的差别，但变化趋势基本一致.图11～图13则给出了优化前后弹性飞机和刚体飞机的诱导阻力、配平型阻以及全机阻力随速度的变化曲线.由图可知，在飞行速度15m/s～25m/s范围内，优化后弹性双尾撑飞机的诱导阻力、配平型阻及全机配平阻力较优化前均有减小.而优化后刚体双尾撑飞机的配平型阻较优化前有所增加，这是因为刚体情况下，升降舵的操纵效率高，所需升降舵配平偏角较小.优化机翼的几何扭转角引起低头力矩的变化，从而改变了升降舵的配平偏角，增加了升降舵配平型阻.

4 结论

1)相同飞行速度下，双尾撑布局弹性飞机的尾撑纵向弯曲刚度越大，全机诱导阻力系数、配平舵偏型阻系数、全机阻力系数就越小，平尾产生的诱导阻力占全机诱导阻力的比例也越小，出于减阻目的考虑应尽可能提高尾撑刚度.

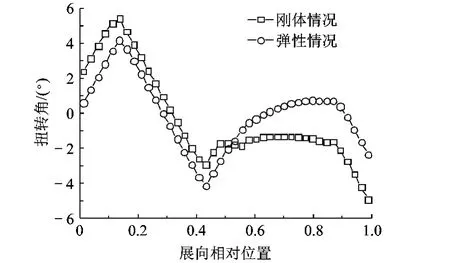
图10 刚体/弹性双尾撑飞机机翼几何扭转角优化结果

图11 刚体/弹性双尾撑飞机优化前后全机诱导阻力系数对比

图12 刚体/弹性双尾撑飞机优化前后升降舵配平舵偏型阻系数对比

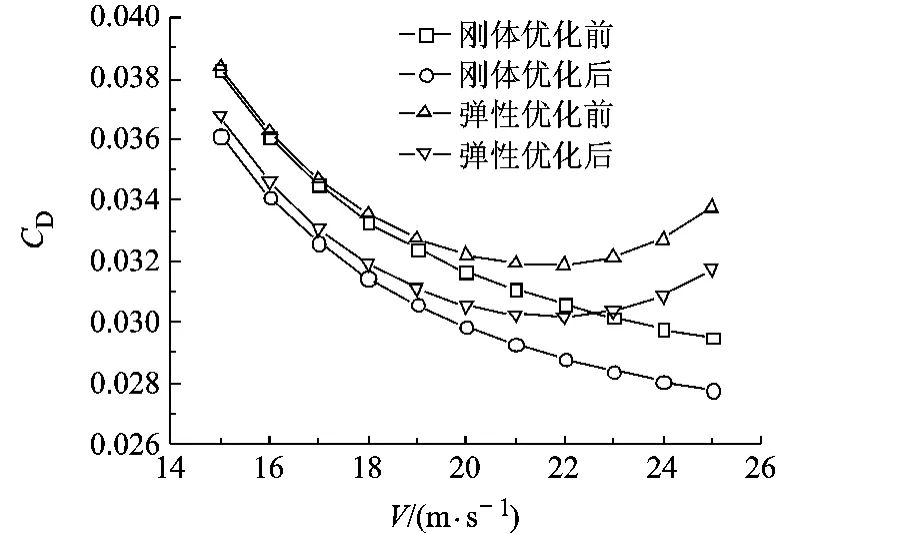
图13 刚体/弹性双尾撑飞机优化前后全机阻力系数对比

2)尾撑纵向弯曲刚度较大时，全机诱导阻力系数随飞行速度的增加而单调减小，而尾撑纵向弯曲刚度较小时，升降舵操纵效率对飞行速度增加而快速降低，会造成全机诱导阻力系数随飞行速度的增加呈现先减小后增加的情况.升降舵配平型阻随飞行速度的增加单调增大.

3)通过机翼几何扭转角的优化配置，可使全机沿展向升力分布更好地接近标准椭圆分布，进而有效减小全机诱导阻力.

由于本文方法考虑的是无粘流的情况，与粘性摩擦相关的零升阻力和配平型阻使用了经验公式进行计算，更精确的分析有待进一步研究.

References)

［1］Phillips W F.Lifting－line analysis for twisted wings and washout－optimized wings ［J］.Journal of aircraft，2004，41(1):128－136

［2］Cusher A A，Gopalarathnam A.Drag reduction methodology for adaptive tailless aircraft［R］.AIAA 2006－3320，2006

［3］陈磊，吴志刚，杨超，等.减小弹性机翼诱导阻力的多控制面优化研究 ［J］.工程力学，2009，26(10):191－196

Chen Lei，Wu Zhigang，Yang Chao，et al.Induced drag reduction optimization study using multi－control surfaces for elastic wing［J］.Engineering Mechanics，2009，26(10):191 －196(in Chinese)

［4］Pfeiffer N J.Numerical winglet optimization［R］.AIAA 2004－0213，2004

［5］Kusmina S，Ishmuratov F，Kuzmin V.Minimization of induced drag of elastic airplane ［R］.AIAA 2004－4611，2004

［6］Roskam J.Airplane flight dynamics and automatic flight controls［M］.Lawrence:DAR Corporation，2001:3－4

［7］Waszak M R，Schmidt D K.On the flight dynamics of aeroelastic vehicles ［R］.AIAA 1986－2077，1986

［8］Meirovitch L.Fundamentals of vibrations［M］.New York:McGraw－Hill，2001:268 －275

［9］Joseph Katz，Allen Plotkin.Low－speed aerodynamics［M］.2nd ed.Cambridge:Cambridge University Press，2001:201－204

［10］《飞机设计手册》总编委会.飞机设计手册第6册:气动设计［M］.北京:航空工业出版社，2005:252－325

Editorial board of aircraft design handbook.Aircraft design handbook vol 6:aerodynamic design ［M］.Beijing:Aviation Industry Press，2005:252－325(in Chinese)

［11］陈宝林.最优化理论与算法［M］.2版.北京:清华大学出版社，2005:417－422

Chen Baolin.Theory and arithmetic of optimization［M］.2nd ed.Beijing:Tsinghua University Press:417－422(in Chinese)

［12］肖志鹏，万志强，梁猛，等.双尾撑布局飞机飞行载荷分析［J］.北京航空航天大学学报，2008，34(4):456－459

Xiao Zhipeng，Wan Zhiqiang，Liang Meng， et al.Flight loads analysis of a twin－tailboom aircraft［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(4):456－459(in Chinese)