模糊相似关系下变精度模糊粗糙集

邓廷权，杨成东，张月童

(1.哈尔滨工程大学理学院，黑龙江 哈尔滨 150001;2.哈尔滨工程大学计算机科学与技术学院，黑龙江 哈尔滨 150001;3.临沂大学 信息学院，山东 临沂 276000)

Z.Pawlak［1］于 1982 年提出的粗糙集是一种有效的软计算工具，已经广泛应用于决策分析、数据挖掘、机器学习和人工智能等各个领域.随着理论研究的深入和应用的需求，经典粗糙集有了进一步的拓展，其中变精度粗糙集和模糊粗糙集是2种典型的代表.

从实际应用的角度而言，由于数据获取或数据处理方面的原因，信息系统或数据库中不可避免地含有噪音，而经典粗糙集对噪音数据比较敏感.鉴于此，1993年 W.Ziarko［2］引入了集合的相对错误包含度的概念，并提出了变精度粗糙集模型，该模型有效地解决了人为错误或噪音导致的错误分类问题，具有较好的抗噪和容错能力.

经典粗糙集处理的是清晰(分明)的、离散的符号值数据，但在实际中经常遇到连续的、具有模糊性的数据.对于这类问题，经典做法是将连续的属性值离散化后运用经典粗糙集处理，这种方法造成了一定的信息损失.模糊粗糙集［3-5］将粗糙集和模糊集理论结合起来，利用数据相似性程度作为数据间的相似关系，从而避免了连续属性值离散化带来的信息损失.

变精度模糊粗糙集［6-9］是变精度粗糙集与模糊粗糙集的融合.它不仅具有变精度粗糙集的特点，具有一定的抗噪和容错能力，也具有模糊粗糙集的特点，能够处理具有模糊性的知识.

然而，变精度模糊粗糙集是基于模糊等价关系建立的.在实际应用中，很难直接构造模糊等价关系，往往先构造模糊相似关系，再通过求模糊相似关系的传递闭包将其模糊等价关系.文献［10］指出，这种方法会丢失较多有价值的信息.因此，研究模糊相似关系下的变精度模糊粗糙集模型具有重要的意义.

1 基础知识

首先回顾经典粗糙集模型.

定义1［1］设U是有限论域，R是U上的一个等价关系，X⊆U，X的R下近似和R上近似分别定义为.集合称为X的R边界域;称为X的R正域;称为X的R负域.显然，

在经典粗糙集模型基础上，W.Ziarko提出变精度粗糙集模型，增强了模型的抗噪和容错能力.

定义2［2］设U是有限论域，R是U上的一个等价关系，0≤β ＜0.5，X⊆U，定义X的 β 下近似和β上近似分别为

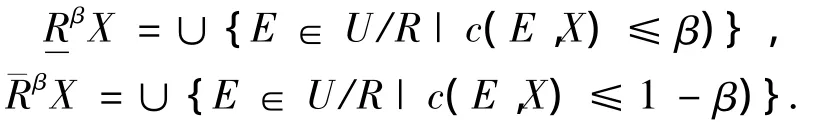
式中:c(X，Y)为集合X和Y的相对错误包含度，定义如式(1)

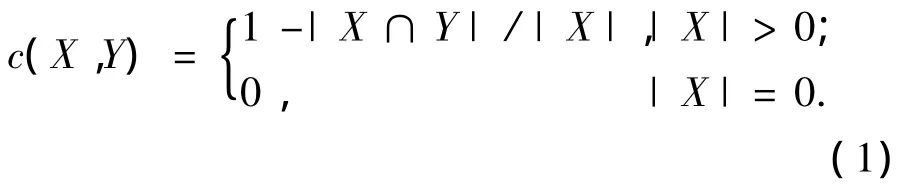
式中:|X|为集合X的基数.

2 模糊集的相对错误包含度

论域U的全体模糊子集组成的集合称为U的模糊幂集，记作F(U).给定论域U和V，则U×V的模糊子集R∈F(U×V)是一个模糊关系.一个模糊关系R称为模糊相似关系，若R满足:

1)自反性:R(x，x)=1，∀x∈U;

2)对称性:R(x，y)=R(y，x)，∀x，y∈U.

模糊相似关系R通常不满足传递性，即R不满足R◦R⊆R.若满足传递性，则称R为模糊等价关系.

模糊逻辑算子是模糊集理论和模糊逻辑中的重要概念，在模糊信息分析和处理中具有重要应用.T-范数和模糊蕴含是2种重要的模糊逻辑算子.

若*满足1)交换律;2)结合律;3)关于2个变量都是递增的;4)边界条件:0*b=0;1*b=b对任意b∈［0，1］成立，称［0，1］上的二元运算* 为T-范数.若→满足1)边界条件:1→0=0，0→0=0→1=1→1=1;2)关于第1个变量单调递减，关于第2个变量单调递增，称［0，1］上的二元运算→为模糊蕴含算子.

有很多T-范数和模糊蕴含算子［11］.比如

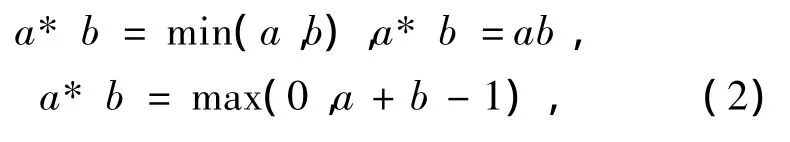
都是典型且常用的T-范数.模糊蕴含算子常通过T-范数以如下方式构造:

1)负蕴含:a→b=1－T(a，1－b).

2)剩余蕴含:a→b=sup{λ∈［0，1］|a* λ≤b}，其中sup为集合的上确界.

本文只考虑T-范数的模糊剩余蕴含算子.式(2)对应的模糊剩余蕴含算子分别为:

为了处理模糊信息，本文首先定义了基于模糊逻辑算子的模糊相对错误包含度的概念.

定义3 设F1和F2是有限论域U上的模糊子集，即F1，F2∈F(U).模糊集F1和F2的相对错误包含度e(F1，F2)定义为

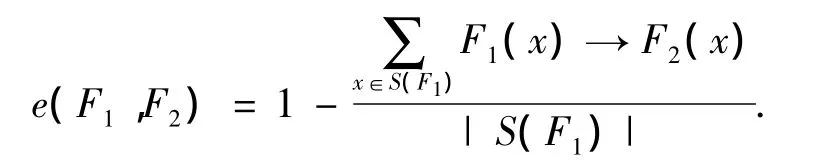
式中:S(Fi)为支集，即S(Fi)={x∈U|Fi(x)＞0}.

定义3中的模糊相对错误包含度是定义2中分明集合的相对错误包含度在模糊集中的推广.

命题 1 对∀F，F1，F2∈F(U)，若F1⊆F2，则e(F，F1)≥e(F，F2).

证明 当F=∅时，e(F，F1)=e(F，F2)=0.当F≠∅时，因为F1⊆F2，则对于任意的x∈U，有F1(x)≤F2(x).由→算子定义可知，它是关于第2变量递增的.所以，

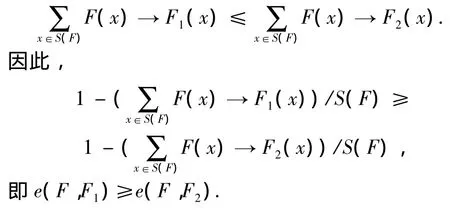
3 模糊相似关系下变精度模糊粗糙集

定义4 设U是有限论域，F(U)是U的模糊幂集，R是U×U上的模糊相似关系.∀F∈F(U)，F关于R的β下模糊近似RβF与β上模糊近似F分别定义为:

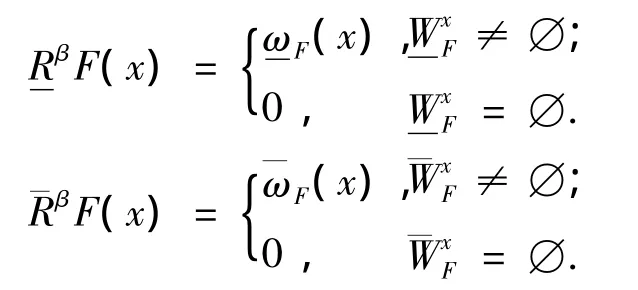
式中:β是精度控制参数，0≤β≤0.5;

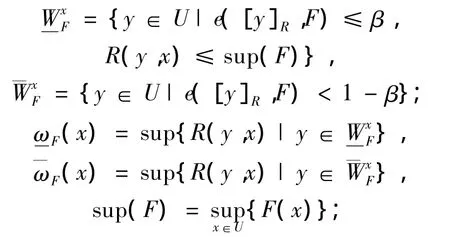
当R为U上的经典等价关系，F为U的分明子集且0≤β＜0.5时，定义4退化为定义2;当R为经典等价关系，F为U的分明子集且β=0时，定义4退化为定义1.因此，有下面2个命题.

命题2 当R为U上的经典等价关系，F为U的分明子集，0≤β＜0.5时，该模型退化为Ziarko变精度粗糙集模型.

证明 仅证β下模糊近似可以退化到Ziarko下近似，β上模糊近似可以退化到Ziarko上近似的证明类似.用RZF表示集合F在Ziarko模型下的β下近似

βRZβF=∪{E∈U/R|c(E，F)≤β}，经典等价关系R和分明子集F分别为特殊的模糊关系和模糊集.下面证明RβF(x)=1，当且仅当x∈RZβF.

对于∀x∈RZβF，则∃E∈U/R，使得x∈E且c(E，F)≤β.若E⊆F，那么e(E，F)=0;若c(E，F)≤β，根据定义 1 可知，e(E，F)≤β，即x∈WxF.根据ωF(x)的定义可知，RβF(x)=1.

反之，若RβF(x)=1，则 ∃y∈U，使得e(［y］R，F)≤β，且R(y，x)=1.

由于R是经典的等价关系，所以［y］R就是y的等价类且x∈［y］R.

根据经典集合的相对错误包含度与模糊相对错误包含度的定义可知，

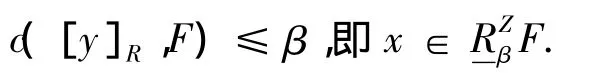
证毕.

命题3 当R为经典等价关，F为U的分明子集，β=0时，该模型退化为Pawlak粗糙集.

证明同理于命题2.

4 变精度模糊粗糙集的性质

下面研究新建立的变精度模糊粗糙集的性质.

性质1 当0≤β＜0.5时，β模糊近似有以下性质:

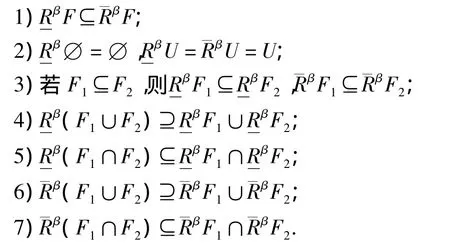
证明 1)∀x∈U，若WxF=∅，那么RβF(x)=0，显然RF(x)≤F(x).若Wx≠∅，则∀y∈Wx，βFF都满足e(［y］R，F)≤β.由于 0≤β ＜0.5，所以e(［y］R，F)≤1－β，即y∈.根据RβF与F的定义可知，RβF(x)≤F(x).

由x的任意性得RβF⊆F.

2)∀x∈U，若Wx=∅，因为sup(∅)=0，所以∅对于∀y∈WxF，都有R(y，x)≤sup(∅)=0，根据ωF(x)的定义，可知R∅(x)=0;若Wx=∅，根据RFβ∅β(x)的定义可知，Rβ∅(x)=0.由x的任意性得Rβ∅ =∅.

由性质1得，RβU⊆U，因此仅需证RβU=U.∀x∈U，都有U(x)=1，所以∀y∈U，都有e(［y］R，U)=0≤β.而R(y，x)≤sup(U)=1，所以WxU=U.由于R是模糊相似关系，所以R(x，x)=1.根据ωF(x)的定义可得，RβU(x)=1.由x的任意性得RβU=U.

3)∀x∈U，若，根据RβF(x)的定义可知，RβF1(x)=0，显然RβF1(x)≤F2(x).

根据RβF(x)的定义可知，RβF1(x)≤RβF2(x)，即

4)由F1∪F2⊇F1，F1∪F2⊇F2和性质 3 可得Rβ(F1∪F2)⊇RβF1，Rβ(F1∪F2)⊇RβF2.所 以，Rβ(F1∪F2)⊇RβF1∪RβF2.

5)由F1∩F2⊆F1，F1∩F2⊆F2和性质 3 可得Rβ(F1∩F2)⊆RβF1，Rβ(F1∩F2)⊆RβF2.因此，Rβ(F1∩F2)⊆RβF1∩RβF2.

6)证明过程同性质4)的证明过程.

7)证明过程同性质5)的证明过程.

2)β上模糊近似和β下模糊近似与 经典变精度相同，也不满足扩张性和反扩张性.

显然RβF⊄F⊄F.因此，β上模糊近似和β下模糊近似也不满足扩张性和反扩张性.

3)β上模糊近似和β下模糊近似与经典变精度相同，也不满足幂等性.

仍取2)中的例子，按照定义可以计算得Rβ(RβF)={0.6，0.92，0.73，0.92，0.85}.

显然Rβ(RβF)≠RβF，所以 β 下模糊近似不满足幂等性.同样，β上模糊近似也不满足幂等性.

例如，取a→b=min(1，1－a+b)，则 β=0.45时，∅={1，0.1，0.2}.因此∅≠∅.这是条件过宽所致，特别地，对模糊蕴含算子加个限制，则空集的上近似为空集.

性质2 若模糊蕴含算子满足s→0=0(s＞0)，则∅=∅.

证明 根据模糊相对错误包含度的定义可知，若s→0=0(s＞0)，则e(F1，F2)=1.因为［x］R≠∅，所以∀x∈U，都有e(［x］R，∅)=1.由于0≤β ＜0.5，所以没有y∈U满足e(［y］R，∅)＜1 － β，即Wx∅=∅.根据F(x)的定义可知，∅(x)=0.综上所述，∀x∈U，都有∅(x)=0，即∅=∅.

性质3 若0≤β1＜β2＜0.5，则

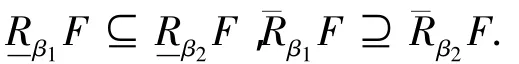
证明记为在 β1精度下的WxF记为在β 精度下的Wx.2F

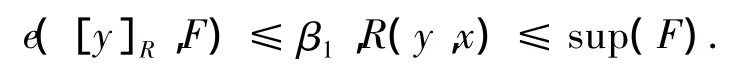
由于0≤β1＜ β2＜0.5，所以e(［y］R，F)≤β2，因此由RβF(x)的定义得Rβ1F(x)≤Rβ2F(x)，e(［y］R，F)≤1－β，即y∈.根据定义4可得RβF(x)≤F(x).

同理可证

R¯β1F⊆F.

5 结论

本文研究了基于模糊相似关系的变精度模糊粗糙集模型.用模糊相似关系来刻画未知的集合.新的变精度模糊粗糙集模型有如下优势:

1)该模型是对变精度粗糙集的一般化和模糊化;

2)该模型既能够处理连续值模糊信息，又具有一定程度的抗噪和容错能力;

3)该模型是基于模糊相似关系建立的，不需要对论域进行任何形式的划分，而是用模糊相似矩阵表示模糊信息，具有更大的灵活性和实用性.

［1］PAWLAK Z.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11:341-356.

［2］ZIARKO W.Variable precision rough set model［J］.Journal of Computer and System Science，1993，46(1):39-59.

［3］DUBOIS D，PRADE H.Rough fuzzy sets and fuzzy rough sets［J］.International Journal of General Systems，1999，17:191-209.

［4］郭海刚，高井贵，张振良.模糊相似关系下的模糊粗糙集［J］.辽宁师范大学学报:自然科学版，2006，29(3):289-291.GUO Haigang，GAO Jinggui，ZHANG Zhenliang.Fuzzy rough sets based on fuzzy similar relation［J］.Journal of Liaoning Normal University:Natural Science Edition，2006，29(3):289-291.

［5］米据生，吴伟志，张文修.粗糙集的构造与公理化方法［J］.模式识别与人工智能，2002，15(3):280-286.MI Jusheng，WU Weizhi，ZHANG Wenxiu.Constructive and axiomatic approaches of the theory of rough sets［J］.Pattern Recognition and Artificial Intelligence，2002，15(3):280-286.

［6］李凡，刘启和，杨国玮.变精度模糊粗糙集的一种定义［J］.控制与决策，2008，23(11):1206-1210.LI Fan，LIU Qihe，YANG Guowei.Definition of variable precision fuzzy rough sets［J］.Contro1 and Decision，2008，23(11):1206-1210.

［7］张东星，苗夺谦，李道国，等.基于数据库系统的可变精度粗糙集模型［J］.计算机科学，2005，32(12):172-174.ZHANG Dongxing，MIAO Duoqian，LI Daoguo，et al.A variable precision rough set model based on database system［J］.Computer Science，2005，32(12):172-174.

［8］黄春娥，张振良.基于截集的变精度模糊粗糙集模型［J］.模糊系统与数学，2004，18(9):200-203.HUANG Chune，ZHANG Zhenliang. Variable precision fuzzy rough set model based on cut set［J］.Fuzzy Systems and Mathematics，2004，18(9):200-203.

［9］冯林，王国胤.用于数据分析的变精度模糊粗糙模型［J］.西南交通大学学报，2008，43(5):582-589.FENG Lin，WANG Guoyin.Variable precision fuzzy rough model for data analysis［J］.Journal of Southwest Jiaotong University，2008，43(5):582-589.

［10］王熙照，赵素云.基于相似关系的模糊粗糙集模型［J］.计算机科学，2004，31(10A):31-35.WANG Xizhao，ZHAO Suyun.Modelling fuzzy rough sets based on similarity relation［J］.Computer Science，2004，31(10A):31-35.

［11］尤飞，冯艳宾，李洪兴.模糊蕴涵算子及其构造(I)［J］.北京师范大学学报:自然科学版，2003，39(5):606-611.YOU Fei，FENG Yanbin，LI Hongxing.Fuzzy implication operators and their construction(I)［J］.Journal of Beijing Normal University:Natural Science，2003，39(5):606-611.