城市交通最优路径算法

陈亮，何为，韩力群

(北京工商大学计算机与信息工程学院，北京 100048)

路径优化是路径规划的核心问题，目前应用最广泛的是1959年Dijkstra［1］提出并以其名字命名的Dijkstra算法，可以解决带有非负代价函数值的路网中的单源最短路径，但是Dijkstra算法的复杂度为O(n2)［2］，由于路径规划要求实时性，因此人们在Dijkstra算法基础上进行各种改进，如进行启发式搜索的A*算法［3］、在记忆路径基础上的启发式搜索算法D*算法［4］等，但是这些算法通常只给出一条最优路径.

本文在路径规划的过程中，利用图的深度优先遍历［5］算法，寻找源点与终点的所有可达路径，并通过限制搜索的路网节点规模和限制搜索方向的规则，进行算法的优化，最后计算得到所有可达路径的代价函数值，并按照从小到大的顺序进行排序.

在将本文的算法应用至实际交通网络中时，为了避免大规模稀疏网络造成计算时间延长，在应用优化的可达路径算法时，将道路网络分成2个级别，得到了较好的效果.利用VC++6.0对算法进行仿真，将未经优化的算法与优化算法的结果进行比较，并用实例验证，表明本文的算法能够很好地实现实时性与最优有效性.

1 可达路径优化算法

1.1 各种存储方式的比较

路径优化问题首先要将实际道路的拓扑结构，通过一定的计算机存储结构进行映射.主要的存储结构形式有邻接矩阵、邻接链表、十字链表、邻接多重链表［6-7］.

邻接矩阵的优势在于容易判断2点间的关系，但缺点是存储稀疏图所占用的空间过大，并且算法时间复杂度较高，为O(n2+m*n)，这对于实际应用中具有成千上万个节点的交通路网图并不合适.十字链表和邻接多重链表要求的存储空间都非常小，但是本身结构较为复杂，在实际中应用也比较有限.

邻接链表的实现方法是链表，缺点在于不易判断2点间的关系，但是对于关联点的查询较为有效，优点是节省存储空间，算法时间复杂度为O(m+n).因此适用于实际交通网络这类大型稀疏图，本文采用的存储方式就是邻接链表［8］.

1.2 路径代价函数值的计算

源点和终点间的所有可达路径中，路径总代价函数值最小者即为最优路径.可达路径的总代价函数值是全部构成路段的代价函数值的总和，此外，由于交叉路口对转向的种种限制，延误时间可达到总时间的17% ～35%［9］，因此在计算每条可达路径的代价函数值时，还必须考虑交叉口转向因素的影响.

在作者前期的工作中［10］，已利用RBF神经网络方法建立了路段的代价函数模型，将5种道路属性作为影响因素设为RBF网络的输入，网络输出为路段代价函数值，这5种道路属性包括:道路交通实时路况、车道数、自助红绿灯数、路段长度及车辆转向方向对行车代价函数值的影响，从而为计算整条路径的总代价函数值打下了基础.

但是，计算整条路径代价函数值的难度在于每一条路段的代价函数值是在已知转向的情况下得到的结果.因此，本文通过建立前向关联边，并采用查表的方法解决每一条路径总的代价函数值的计算［11］，即将3个点之间的关系两两合并，得出二维数组的行数和列数，然后将每一段加起来，即可得到每一条路径的代价函数值.特别地，在终点和它上一个节点的代价函数值的计算中，设置了一个数组存放最后一段路段的代价，因为通常到达了终点不存在选择方向的问题，从而将这个数组中的值设置为直行的代价函数值.以图1为例，进行简单说明.

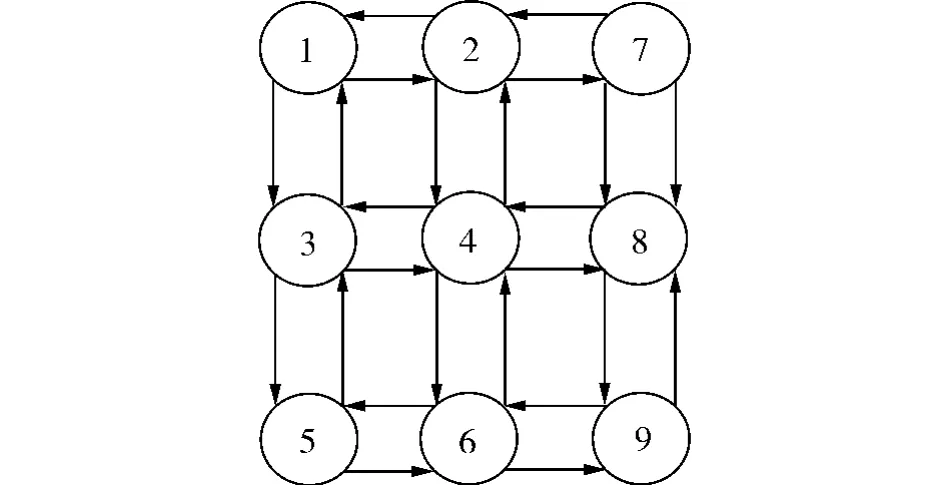
图1 有向图Fig.1 Directed graph

选取图中的1、2、3、4、5 点作说明，如图 2 所示.例如:节点1指向节点2、3，那么节点1的指针指向节点序列中的2、3，依此类推，将转向条件计入在下一个节点中，就是图2中代价函数值所代表的.

图2 前向关联边结构及其对应代价函数值Fig.2 Associated side of the structure and its cost function value

根据指针对应的节点序列找到二维数组的行，再通过下一结点的偏移量找到对应的二维数组的列，即可求出每一段路径的代价函数值，最后将路径中每一路段的代价函数值加起来，就得到了整条路径的代价函数值，然后根据代价函数值从小到大对可达路径进行排序并显示出来，供使用者参考选择［12］.

1.3 城市交通可达路径算法的优化

本文采用深度优先遍历算法求得交通图中任意2点之间的所有可达路径，具体通过深度优先遍历算法中的迭代算法来实现.迭代算法利用一个堆栈S来记录访问过程，当初始点(源点)压入栈后，并建立一个visit［］数组来标记节点是否被访问过，然后进行迭代，步骤如下:

1)检测堆栈是否为空，若堆栈为空，则迭代结束;否则，进行下一步;

2)访问源点的邻接表中的点，找出visit［v］为0的点v，将其标记为源点的下一节点，并置visit［v］的值为1，判断v是否为终点，如是，则弹出终点，并记录路径数组route［］，否则进行下一步;

3)求v的邻接点表，将v未被访问过的邻接顶点压入栈，同样进行判断v是否为终点，如是终点则弹出，记录路径，否则进行下一步;

重复进行1)～3).

设计程序流程如图3所示.在此过程中，每一个节点都已经记录了上一个节点，即route［v］，算法结束后，逆序打印每一条路径，即可得到图中任意2点间的所有可达路径.

上述算法并不复杂，对于有向图中寻找任意2点间所有可达路径十分有效.但是该算法存在2个问题:1)搜索很多冗余可达路径，不符合常理的“绕路”路径;2)算法的效率有待提高.针对这2个问题，本小节将研究优化算法的有效规则.

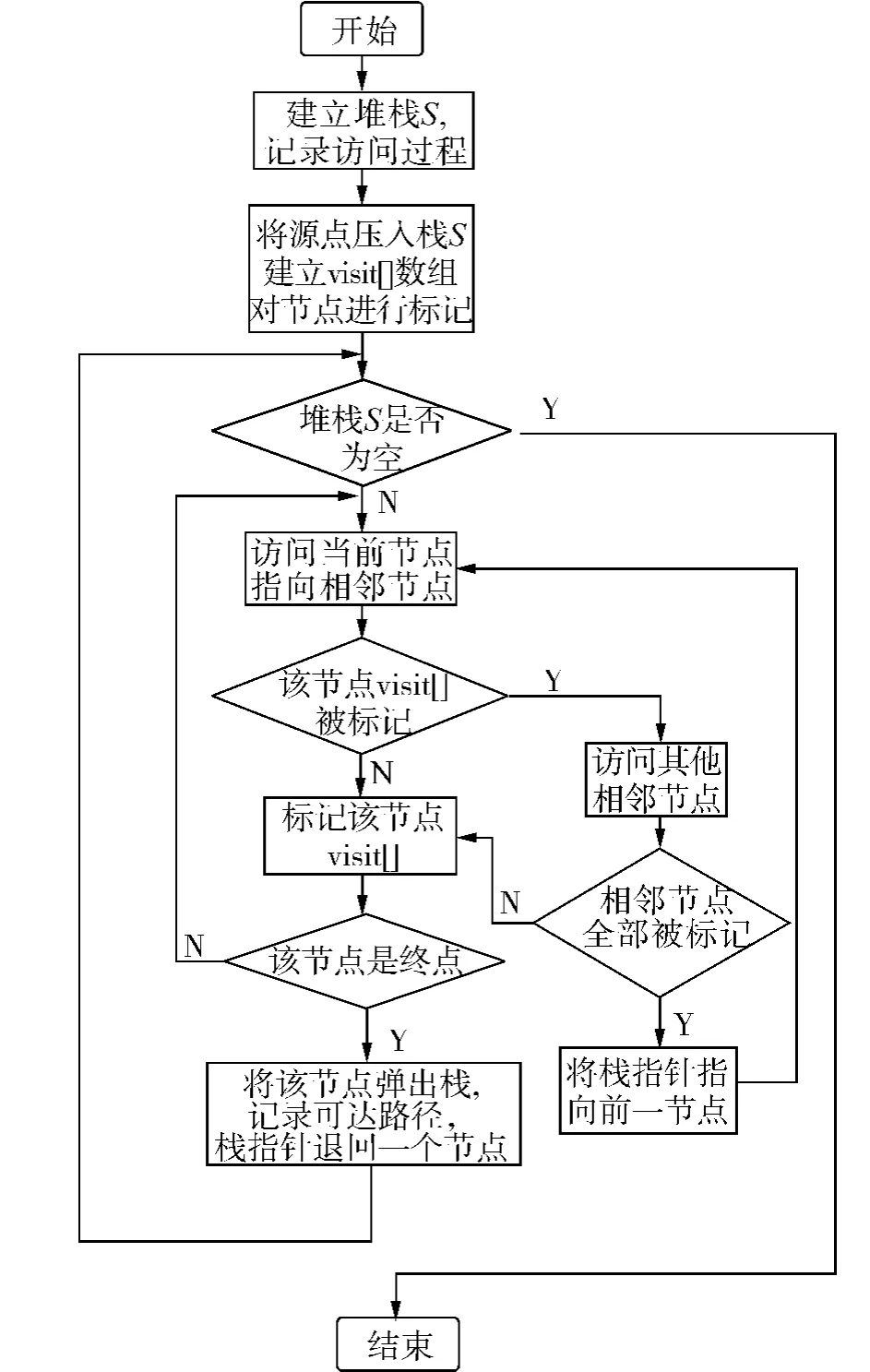
图3 可达路径搜索算法流程Fig.3 The flowchart of reachable route searching algorithm

1.3.1 城市交通有向图映射至邻接链表

在作者之前的工作中［10］，已经解决了如何将城市交通路网图抽象为城市交通有向图，但是无法以数据元素在存储区中的物理位置来表示元素之间的关系.可达路径算法优化问题，首先要将实际道路的拓扑结构通过一定的计算机存储结构进行映射，其具体步骤如下:

1)设定节点信息.

首先定义节点信息，包括节点号、方位、指向下一节点、在地图中的横纵坐标.

2)定义栈并将节点压入栈.

将设定好的节点，按照城市交通有向图连接关系，压入栈中.

3)建立前向关联边结构.

根据城市交通有向图，按照1.2节所示，建立前向关联边结构.

经过这3个步骤，一张城市交通网络有向图已经映射至计算机的存储结构中.

1.3.2 城市可达路径算法优化

在深度优先遍历搜索可达路径算法的基础上，结合城市道路交通有向图，制定3条优化规则，分别是限制搜索区域、限制可达路径的搜索方向、地图分级搜索，下面来分别解释这3条优化规则.

1)限制搜索区域.

对于实际节点数量非常庞大的实际交通图，如果遍历所有图中的节点，则将会导致计算量与计算时间成倍增加，因此，将交通图的搜索区域限制在一定范围内，可以达到交通诱导系统的实时性要求［13］.

利用已有的节点坐标信息，将搜索的区域设定为以源点和终点连线为对角线的矩形范围内，但是考虑到有时需要从源点先绕行至矩形范围以外的节点路径;因此，将矩形范围扩大一个节点范围，如图4所示.图中的虚线范围是以源点和终点为对角线的矩形，实际限制范围为虚线矩形向外扩一个节点的距离，即图中粗实线矩形范围.

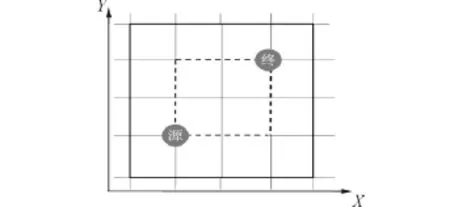
图4 限制搜索区域Fig.4 Limit searching area

2)限制节点的搜索方向.

源点与终点之间的距离会呈现东西方向相距较远，或者南北方向相距较远，例如，驾驶者在由东向西行走东西向较长的道路时，一般情况下不会再想到往西回绕道路，因此将这种相反的方向限制住.进一步，限制节点的2个搜索方向，即以源点和终点连线为向量，限制这个向量的2个分量:第1种情况，当源点和终点的距离为南北向相距较远时，禁止方向为反向;第2种情况，限制2个方向的示意图如图5所示.

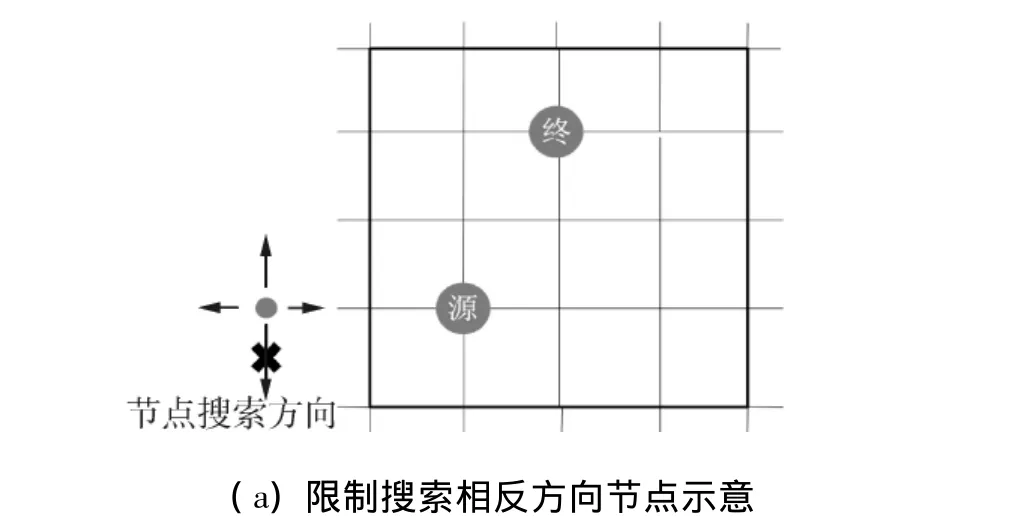
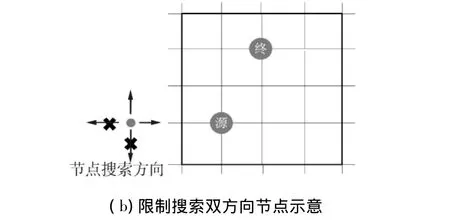
图5 限制节点搜索方向示意Fig.5 Limit node searching direction diagrams

驾驶者从起点出发时，有时会先向路况较好的相反方向行驶一段路程，这也可能是最优路径，因此不限制源点的行驶方向.

3)路网分级搜索.

路网分级方法:交通管理部门将城市道路分为4个级别，分别是国道以及城市快速路、城市主干路、次干路、支路.本文选取了一级路网和二级路网，即国道以及城市快速路、城市主干路作为主要研究对象，因为低级别道路的实时交通路况不易获得，所以暂不将低级别路网考虑进入路径规划中.

实际的交通路网是庞大的稀疏网络，如果考虑将所有的道路节点都包含进算法计算最优路径，势必会影响算法的效率;因此，采用将路网分级的方法，减少搜索节点的数量，提高算法效率，城市交通路网分级示意图如图6所示.

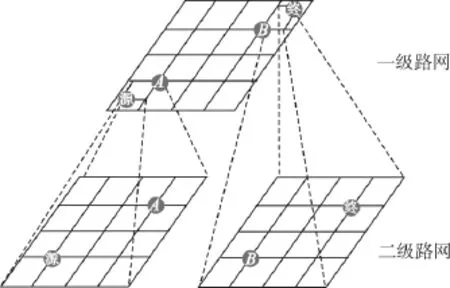
图6 路网分级搜索示意Fig.6 Road network classification search diagram

具体搜索方法如图7所示，应用本文的可达路径搜索算法，计算出源点与A点之间的最优路径，再找到一级路网中A、B2节点之间的最优路径，最后确定B点与二级路网中的终点之间的最优路径［14-15］.

确定路网范围后，最优路径规划分为2步进行:

1)确定节点.将距离源点和终点最近的2个二级路网节点看作源点与终点，同样，再分别确定一级路网中，距离二级路网源点和终点最近的节点，分别命名为A点和B点.

2)应用可达路径算法.将一级路网看作二级路网的子集，应用本文的可达路径优化算法，计算出源点与A点之间的最优路径，再找到一级路网中A、B2节点之间的最优路径，最后确定B点与二级路网中的终点之间的最优路径.

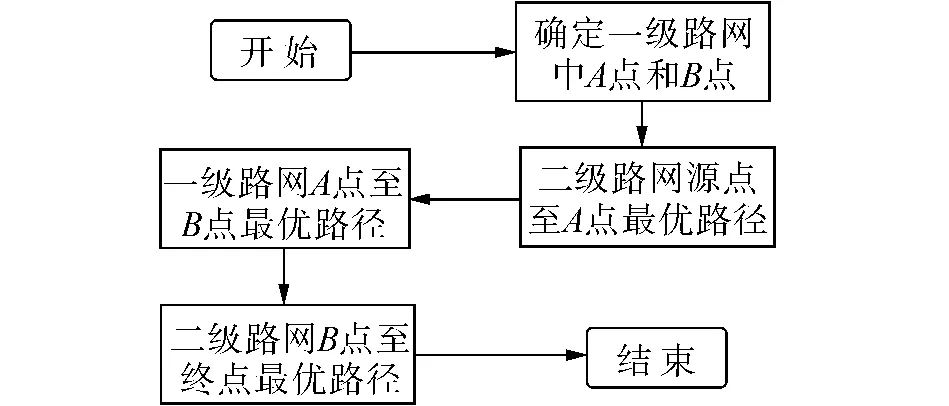
图7 路网分级搜索流程Fig.7 Road network classification flow chart

2 算法有效性验证及应用实例

2.1 算法有效性验证

为了验证算法的有效性以及高效性，本文通过建立北京市五环内的高等级道路路网图数据作实验，如图8所示.由于选取的道路等级较高，在图中共有39个高级别道路节点.编程工具采用Visual C++6.0，硬件环境为 Core2 CPU 2 GHz，内存2 GB.

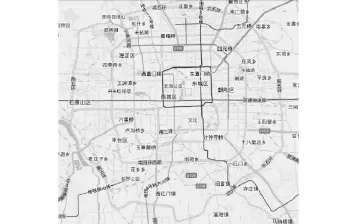
图8 北京市内五环路网Fig.8 Beijing road network within 5th ring map

由表1可知，当不加任何限制条件时，运行时间非常慢，不满足实时性，主要是由于搜索的可达路径数量非常庞大，当加入限制条件后，可达路径的数量减少许多，同时仍然能够找到最优路径，这说明不加限制条件时，深度优先算法会找出许多不符合实际情况的道路，因此加一定的限制条件是可行而且必要的.第2条规则是限制2个方向，现将限制搜索范围作为基础规则，第2条规则与只限制一个方向规则的差异如表2所示.

表1 限制规则结果对比Table 1 Limit rules results comparison

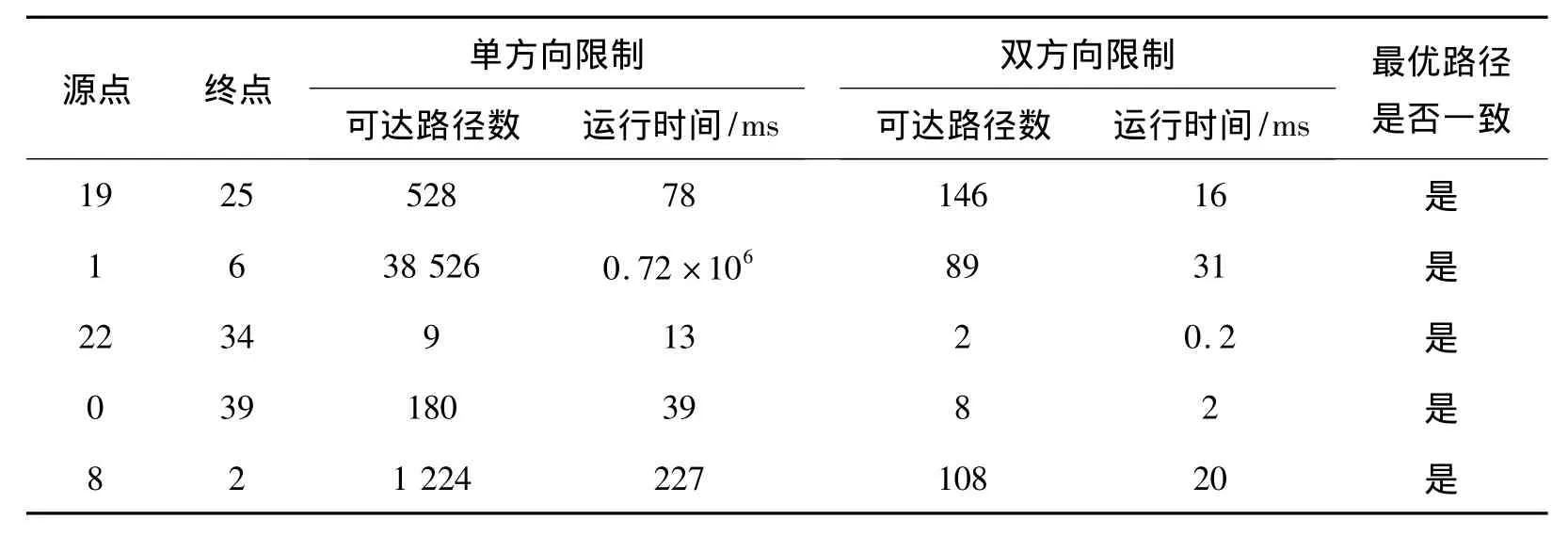
表2 单方向与双向限制结果对比Table 2 One-direction and two-direction limit searching results comparison

由表2可知，限制双方向行驶规则的运行时间较单方向限制的规则成倍地减少，虽然2种规则下给出的路径排序不完全相同;但是这2种规则下给出的最优路径是相同的，这就保证了算法的有效性，而且大大缩短了算法的运行时间，证明了双方向限制条件符合车辆诱导系统的实时性要求.

2.2 应用实例

本文的实例选取的是从北京市大兴区的康盛园至海淀区的北京工商大学阜成路校区.

1)按照最优路径规划的步骤，首先确定节点.图9(a)中，五角星为源点，一级道路上的节点为A点.

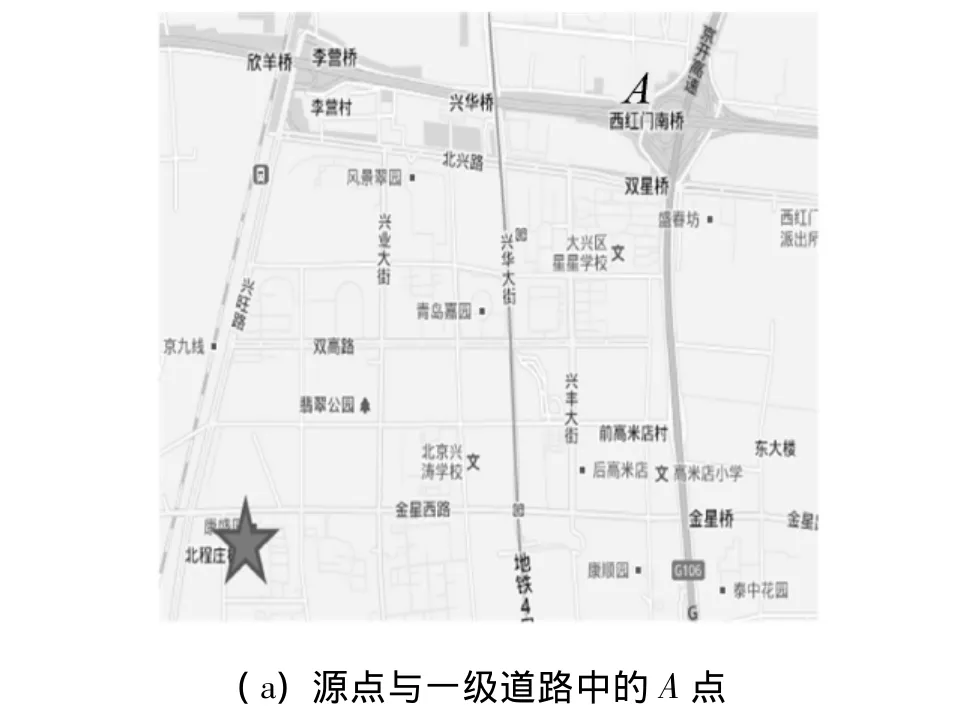
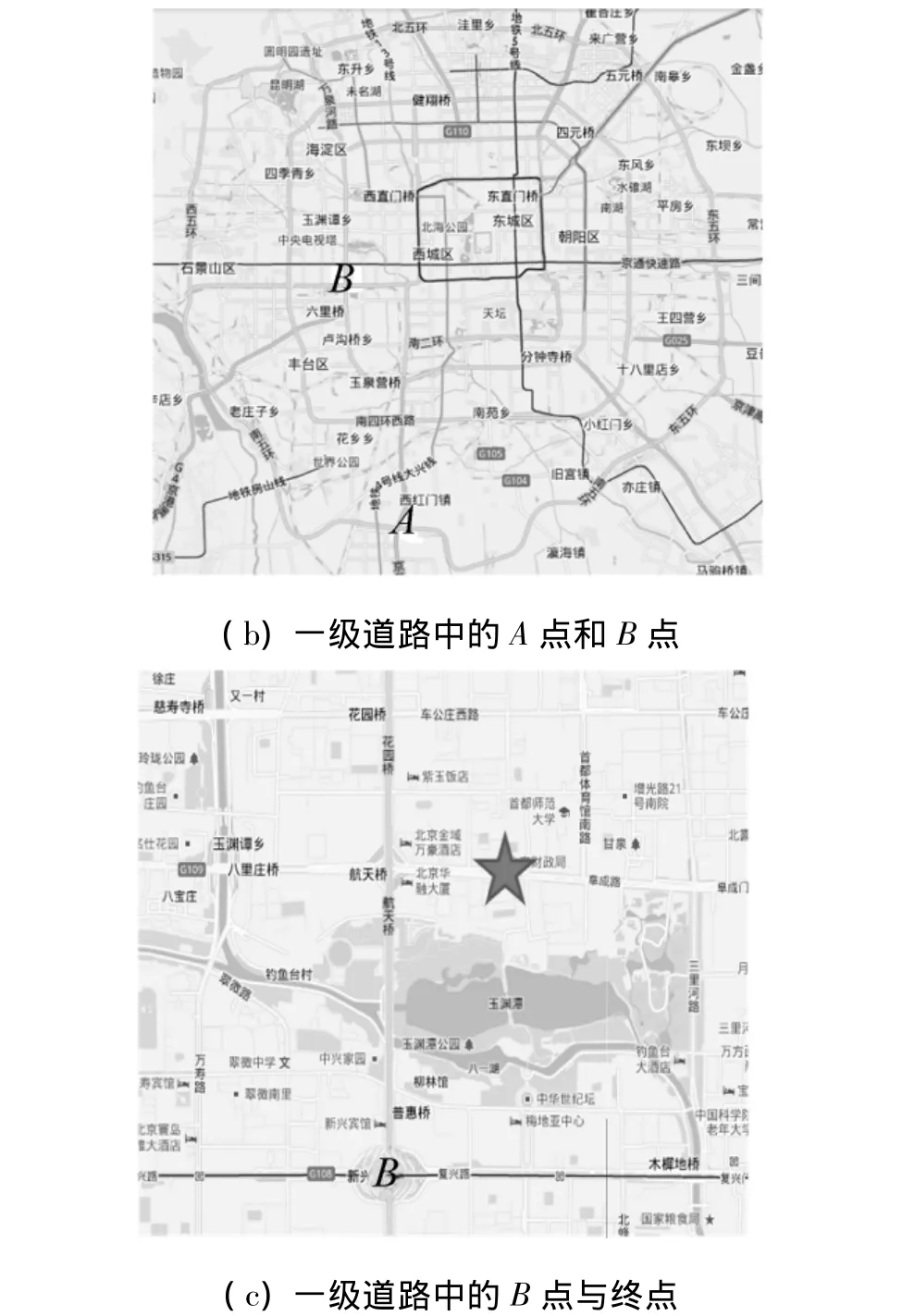
图9 地图分级搜索路径Fig.9 Map hierarchical searching diagram

2)分别找出图9(a)、(b)、(c)中的可达路径，算法的计算时间如表3所示.

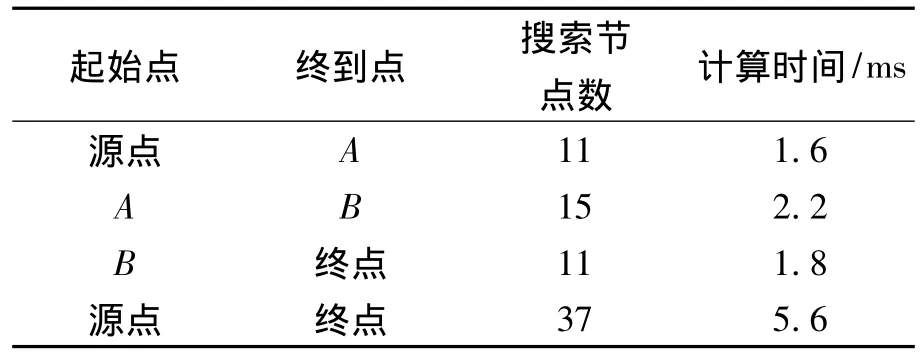
表3 可达路径计算时间Table 3 Reachable path calculating time

由表3可知，算法总共的运行时间为5.6 ms，主要是由于优化后的算法将搜索的节点数控制在较小的范围内，从而达到了提高搜索效率的目的，通过本例，进一步验证了本文所提出算法的有效性与高效性.

3 结束语

本文提出了一种在城市道路中搜索最优路径的算法，与以往算法不同的是，先考虑了高等级道路网的特点，由于高等级道路节点较少，再加上可达路径算法的优化，因此能够大大降低算法运行的复杂度与运算规模，经验证能够保证算法运行的有效性与高效性，然后将低等级道路网络与高等级道路网络联合考虑，在源点和终点分别优化搜索可达路径，保证了算法应用于整个路网的可行性.

［1］DIJKSTRA E W.A note on two problems in connection with graphs［J］.Numerische Mathematik，1959(1):269-271.

［2］ZHAO Yilin.Vehicle location and navigation system［M］.Boston:Artech House，1997:16-102.

［3］张渭军，王华.城市道路最短路径的Dijkstra算法优化［J］.长安大学学报:自然科学版，2005，25(6):62-65.ZHANG Weijun，WANG Hua.Optimation Dijkstra arithmetic for shortest path of urban traffic net［J］.Journal of Chang’an University:Natural Science Edition，2005，25(6):62-65.

［4］姜桂艳，郑祖舵.基于记忆机制的动态交通路径优化算法［J］.吉林大学学报:工程技术版，2007，37(5):1043-1048.JIANG Guiyan，ZHENG Zuduo.Dynamic traffic path optimization algorithm based on mnemonic mechanism［J］.Journal of Jilin University:Engineering and Technology Edition，2007，37(5):1043-1048.

［5］梁磊.两点间所有路径的遍历算法［J］.科技信息，2010，25(33):86-87.LIANG Lei.All paths between two points of traversal algorithm［J］.Science and Technology Information，2010，25(33):86-87.

［6］谭浩强.C++面向对象程序设计［M］.北京:清华大学出版社，2006:25-60.

［7］严蔚敏，吴伟民.数据结构［M］.北京:清华大学出版社，2003:18-190.

［8］任刚，王炜.交通建模中的最短路径算法研究综述［C］//第一届中国交通地理信息系统技术研讨会.武汉，中国，2007:165-173.REN Gang，WANG Wei.Survey on shortest path algorithms in transportation modeling［C］//The First Session of the China Communications Symposium Geographic Information System Technology.Wuhan，China，2007:165-173.

［9］CALDWELL T.On finding minimum routes in a network with turn penalties［J］.Communication of the ACM，1961，4(2):107-108.

［10］陈亮，何为，韩力群.RBF神经网络的行车路径代价函数建模［J］.智能系统学报，2011，6(5):424-431.CHEN Liang，HE Wei，HAN Liqun.Radial basis function neural network modeling of the traffic path cost function［J］.CAAI Transactions on Intelligent Systems，2011，6(5):424-431.

［11］刘张雷，史忠科.城市动态时间最短路径诱导系统实现研究［J］.控制工程，2010，17(3):351-355.LIU Zhanglei，SHI Zhongke.Implementation of urban time-dependent shortest route guidance system［J］.Control Engineering of China，2010，17(3):351-355.

［12］万玮，刘晔，李立宏，等.采用联合优化方式的最佳路径算法研究［J］.计算机工程与应用，2007，43(30):97-100.WAN Wei，LIU Ye，LI Lihong，et al.Reseach on optimal path search algorithm adopting union optimization method［J］.Computer Engineering and Applications，2007，43(30):97-100.

［13］王亚文，汪西莉，曹菡，等.一种动态限制搜索区域的最短路径规划算法［J］.计算机应用研，2007，24(7):89-91.WANG Yawen，WANG Xili，CAO Han，et al.Shortest route-planning algorithm within dynamic restricted searching area［J］.Application Research of Computer，2007，24(7):89-91.

［14］苗洋，陈奇.嵌入式环境中分层路径规划算法改进［J］.计算机工程，2010，36(14):243-245.MIAO Yang，CHEN Qi.Improvement of hierarchical path planning algorithm in embedded environment［J］.Computer Engineering，2010，36(14):243-245.

［15］苏海滨，张继涛.限制搜索区域的分层路径规划新算法［J］.河南大学学报:自然科学版，2008，38(1):81-84.SU Haibin，ZHANG Jitao.A new algorithm of hierarchical route planning with restricted search area［J］.Journal of Henan University:Natural Science，2008，38(1):81-84.