求解旅行商问题的混合粒子群优化算法

沈继红，王侃

(1.哈尔滨工程大学理学院，黑龙江 哈尔滨 150001;2.哈尔滨工程大学自动化学院，黑龙江 哈尔滨 150001)

优化问题可以自然分为2类:一类是连续变量的优化问题;另一类是离散变量的优化问题，即所谓的组合优化问题.旅行商问题(travel salesman problem，TSP)是组合优化问题中的一个著名NP难题，TSP因其典型性已经成为许多启发式搜索、优化算法的间接比较标准.同时TSP也是一个具有广泛的应用背景与重要理论价值的组合优化难题，对求解该问题高效的全局优化算法的研究，一直被科学界和工程界所高度重视.

TSP问题的求解方法归纳起来可以分为得到最优解的精确算法和找到近似解的近似算法.完全枚举法、动态规划法和全局搜索算法属于精确算法.TSP问题精确算法的运行时间是指数级复杂度，难以适应大规模的实例，随着对TSP问题的认识加深，精确算法的研究越来越少.近年来受到自然界的启发，人们提出了各种各样的计算智能方法，如人工神经网络、遗传算法、蚁群优化算法、粒子群优化算法和人工免疫系统等.智能优化算法为解决TSP问题提供了新的思路，它们被广泛地应用于各种NP难题的优化问题求解，虽然不能保证获取最优解，但在问题规模较大时也可以在可行时间内找到满意的解.

粒子群优化算法(particle swarm optimization，PSO)是一种群智能优化方法，它是由美国社会心理学家Kennedy和电气工程师R.Eberhart在1995年提出的，它利用了生物群体中信息共享的思想，其概念简单、易于实现，同时又有深刻的智能背景，既适合科学研究，又适合工程应用.因此，PSO一经提出，就引起了众多学者的关注，得到了非常广泛的应用.为解决组合优化问题，Kennedy等［1］首先提出了PSO算法的离散二进制版;Clerc［2］提出了求解TSP问题的离散粒子群优化算法，对TSP问题的求解重新定义粒子的位置、速度和相关运算，但其性能与其他算法相比仍有不小的差距;高尚等［3］在粒子群算法中加入遗传算法思想，构造了混合算法;Hendlass等［4］通过对离散PSO的每个粒子增加记忆功能，成功解决了一个小规模的TSP;王康平等［5］通过引入“交换子”和“交换序”的概念，给出了另一种解决TSP的PSO方法，为求解TSP问题提供了新的思路.但在算法的收敛速度方面以及在城市规模较大的情况下，现有文献中的粒子群算法都存在着一定的缺陷，本文试图通过与其他智能优化算法的结合来解决这一问题.光学寻优算法［6］是2007年沈继红教授提出的模拟光自然属性的智能优化算法，利用在可行域中填充正方形介质，模拟光的折射以及反射现象，通过最基本光学定律找到最优值，算法迭代机理简单、收敛速度快，具有很强的并行计算能力.2010年，李焱等［7］给出了基于正六边形网络的光学寻优算法，在高维迭代中具有良好的仿真效果，李加莲等［8］给出了光学寻优算法的基本理论证明，并与其他算法进行了比较，完善了算法的理论体系.本文通过正方形网络光学寻优算法的搜索机制形成初始粒子群，加入混沌优化的思想，并引入“交换子”概念，利用离散粒子群算法求解TSP问题，提出了一种新的解决TSP问题的光学混沌粒子群算法.

1 混合粒子群优化算法的构建

1.1 旅行商问题以及标准粒子群算法

TSP的描述十分简单，即寻找一条最短的遍历N个城市的路径，其数学描述如下:

设有N个城市的集合C={c1，c2，…，cN}，每2个城市之间的距离为d(ci，cj)∈R+，其中 ci，cj∈C(1≤i，j≤N)，求使目标函数

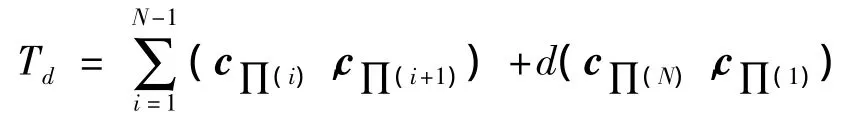
达到最小的城市序列(c∏(1)，c∏(2)，…，c∏(N))，其中，∏(1)，∏(2)，…，∏(N)是1，2，…，N的全排列.

1998年，Shi等［9］给出了标准的 PSO 算法的数学描述:设搜索空间为D维空间，粒子数为n，第i个粒子的位置用 xi=(xi1，xi2，…，xiD)表示;第i个粒子的速度变化率用vi=(vi1，vi2，…，viD)表示;第i个粒子迄今为止搜索的得最好位置为pi=(pi1，pi2，…，piD)，记为pbest，整个粒子群迄今为止搜索到的最好位置为 pg=(pg1，pg2，…，pgD)，记为 gbest，对于每一次迭代，第i个粒子在第D维运动的表达式如下:

式中:c1、c2为正常数，称为加速因子;rand()为［0，1］之间的随机数;w称为惯性因子.第d维的位置和速度的变化范围为［－xdmax，xdmax］和［－vdmax，vdmax］，如果在某一维中迭代的xid、viid超过了取值边界则按照边界取值.

1.2 光学寻优算法

光学寻优算法借鉴了费马定理，利用光在传播过程中自动寻优的机制，将光的折射与反射原理与最优化的寻优过程联系起来，给出一种新的最优化搜索算法.这种算法将坐标空间设想为填充了具有不同折射率的介质的空间，如图1所示，将搜索路径设想为光的传播路径，通过光的折射原理，使搜索方向趋向于目标函数值减小的方向，通过光的反射原理，改变搜索方向，使得搜索在折射无法进行时继续下去.

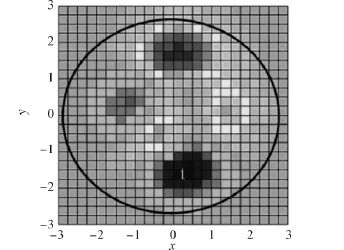
图1 在可行域中填充介质Fig.1 Filling medium in feasible region

针对以下问题进行研究:

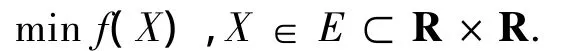
式中:f(X)是正函数，即∀(x，y)∈M，f(x，y)＞0.X是可行解，M是f(X)的可行域，R×R是二维实数空间.P(i)为第i次的搜索方向，h、τ为网格步长.对于第i次迭代，令搜索以P(i)方向在矩形分块Di中搜索到点X(i)=(xi，yi)，并在X(i)点改变搜索方向，到达X(i+1)点，方向的迭代关系满足:

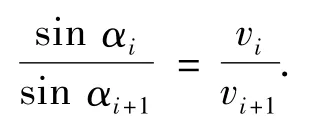
式中:αi为Di中的入射角，αi+1为Di+1中的折射角，vi为光在Di中的传播速度，可设定为Di中X(i+1)=(xi+1，yi+1)点的函数值.vi+1为光在Di+1中的传播速度，可设定为Di+1中X(i+1)=(xi+1，yi+1)点的函数值.

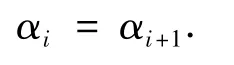
式中:αi为Di中的入射角，αi+1为Di+1中的反射角.图3～4是加入了多个临界面的水平以及竖直方向的搜索路径.光学寻优算法能快速找到最优搜索路径.

图2 基于反射和折射搜索方向的更新Fig.2 Updating searching direction based on reflection and refraction

图3 增加多个临界面光路的更新Fig.3 Updating light line after adding

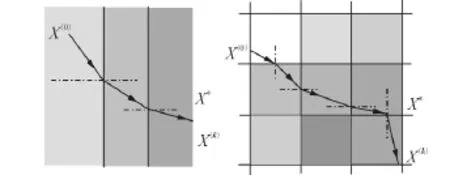
图4 增加水平竖直临界面Fig.4 Adding horizontal and many critical surfaces vertical critical surfaces

1.3 TSP问题中的光学寻优思想

光学寻优算法遵循费马原理，费马原理表明，光在介质中从一点向另一点传播时，总是沿着时间最少的路径，光的传播在不同介质中速度不同，运用光学寻优的思想可以很容易地得到粒子群的一组性能良好的初始粒子，大大减少算法的迭代次数.

定义1 当前城市密度.从当前城市到其他未被遍历过的城市的最短路径.

定义2 前沿城市密度.去除已经遍历的城市，剩余城市路径的平均值.

定义3 TSP问题中的反射.从当前城市开始，随机选择一条与未被遍历城市的路径.

定义4 TSP问题中的折射.从当前城市开始，选择与未被遍历城市之间最短的路径.

光学寻优初始化初始值的过程如下:

1)随机选择一个城市作为出发点，选择与当前城市之间的最短路径城市作为下一个遍历点.

2)计算当前城市密度与前沿城市密度.

3)如果当前城市密度小于前沿城市密度，则发生折射，选择与未被遍历城市之间最短路径城市作为下一个遍历点;如果当前城市密度大于前沿城市密度，随机选择一个未被遍历的城市作为下一个遍历城市.

4)重复3)的过程直到所有的城市都被遍历.

5)将每一个城市都作为起点，依据光学寻优的思想形成N个城市序列，作为混沌粒子群算法的初值.

2 光学混沌粒子群算法

2.1 TSP问题中的混沌粒子群算法

2.1.1 TSP问题中混沌粒子群算法的相关定义

定义5 交换子.2个城市序列［10］Xi=［xi1xi2… xim］与Xj=［xj1xj2… xjm］，如果2个序列在相同的位置，数值不相同，即 xia≠xja，称(xia，xja)为城市序列的交换子，即为Vij(xia，xja).

定义6 交换序列.由交换子组成的序列V=［V1V2… Vn］，其中n为2个城市对应序列相同，但数值不同的位置个数.

定义7 粒子的位置.粒子的位置是由城市序列X=［X1X2… Xm］表示，m为城市的个数;

粒子的速度.粒子的速度V=［V1aV2b… Vmn］，其中Vmn表示交换子，速度为交换序列.

2.1.2 交换子与交换序列的运算法则

1)位置与交换子的加法.

位置与速度的加法形成新的城市序列:设X=［X1X2… Xm］为城市序列，Vij(Xi，Xj)为交换，则

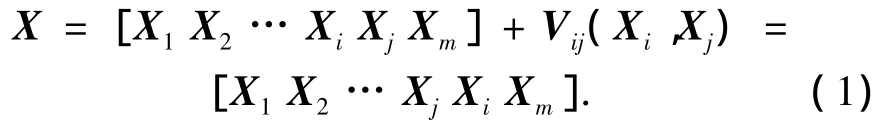
X=［X1X2… XjXiXm］为新形成的城市序列.

例1:

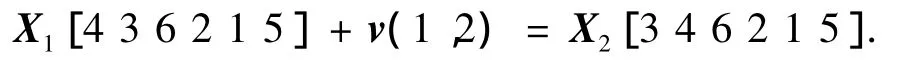
2)位置与位置的减法.

位置与位置的减法形成交换序列即生成新速度:Vij=Xi－ Xj，其中 Xi、Xj为城市序号.先找到与第1个城市序列中第1个元素相同的第2个城市序列位置，形成交换子v(1，i)，然后将此交换子作用在第1个序列上得到新的第1个序列，再找到新的第1个城市序列与第2个城市序列数值相同的第1个位置，形成交换子v(2，i)，依次进行下去，得到2个城市序列的交换序列.

例2:

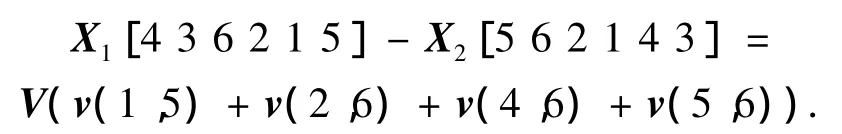
3)交换子的数乘.

速度的数乘具有概率意义，例如Via=c·Vjb，其中c∈［0，1］是一个常数，在计算Via时，对Vjb中的每一维速度Vjn生成一个(0，1)的随机数.

4)混沌思想.

通常一类非常简单却又广泛应用的混沌系统是Logistic 映，其定义如下［11］:

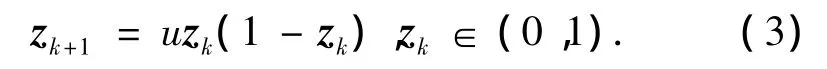
式中:zk为实值序列，u为参数，研究表明当3.571 448≤u≤4时，该混沌映射处于混沌状态，把3.571 448≤u≤4称为混沌区域.Logistic混沌映射所生成的序列具有如下混沌特性:①非周期的序列;②该混沌序列不收敛;③zk可以遍历整个(0，1)区域.

本文取u=4，设城市数量为n，按照顺序随机地生成(0，1)的n个随机数，构成向量序列Z(k)=［z1(k)z2(k)… zn(k)］，将 z1，z2，…，zn按照从小到大排列1，2，…，n的下标号构成城市序列Xi=［Xi1Xi2… Xin］，按照式(1)生成向量，然后对Z(k+1)中元素从小到大进行排列下标号1，2，…，n构成新的城市序列 X(i+1)=［X(i+1)1X(i+1)2… X(i+1)n］.混沌遍历的引入，有效地增加了城市序列的多样性.

例3:

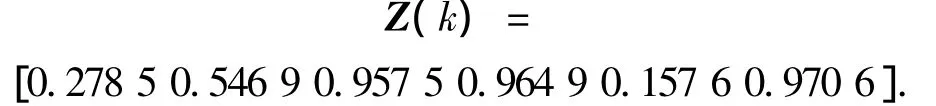
生成的城市序列为Xi=［4 1 2 3 4 6］，运用式(3)，

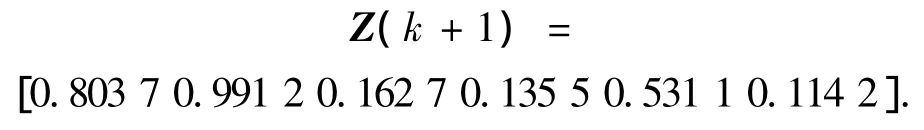
生成新的城市序列为Xi+1=［6 4 3 5 1 2］.

针对TSP问题，结合混沌思想的粒子群的更新公式变为:

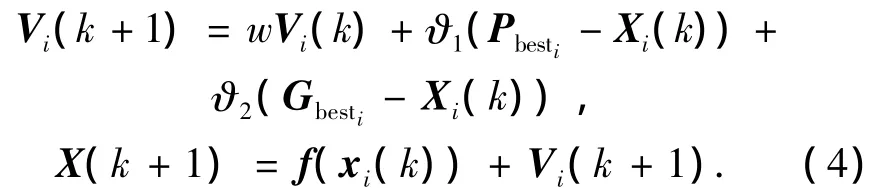
式中:ϑ1、ϑ2为(0，1)的数，f(x)为 xi(k)向量从小到大排列下标形成的向量函数，Xi(k)为当前城市序列，Xi(k+1)为新生成的城市序列，Pbesti为当前个体最好序列，Gbesti为全局最好序列.Pbesti－ Xi(k)=Vp(k)，Gbesti－Xi(k)=VG(k)表示为交换序列，ϑ1(Pbesti－Xi(k))表示当概率小于ϑ1时发生交换操作，当概率大于ϑ1不进行操作，城市序列保持不变.

2.2 光学混沌粒子群算法步骤

1)利用1.3中光学寻优的思想初始化粒子群，从每一个城市出发，得到N个初始值良好的城市序列;随机生成混沌序列Z(1)并运用函数f(x)得到城市序列Xf(1).

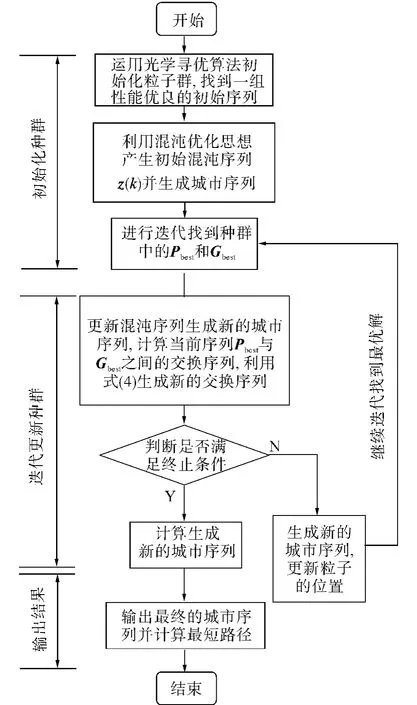
图5 混合粒子群算法的流程Fig.5 A flow sheet of mixed particle swarm algorithm

2)如果满足最优条件，最短城市距离不再变——或者达到最大迭代次数转到5)，如不满足条件对初始种群进行更新，找到个体最好位置Pbesti以及全局最好位置Gbesti.

3)根据式(4)更新城市序列;

①根据式(1)和(3)计算混沌生成序列Z(k)并运用函数f(x)得到新的城市序列Xf(k);

②运用例2的思想计算交换序列，Pbesti－ Xi(k)=Vp(k)，Gbesti－ Xi(k)=VG(k);

③根据式(2)计算 φ1(Pbesti－Xi(k))+φ2(Gbesti－Xi(k));φ1、φ2为执行操作的控制概率.

④根据以上3个结果结合式(4)得到新的城市序列Xi(k+1).

4)迭代次数增加，更新粒子的位置转到2).

5)输出最优城市序列，并输出最短距离.

2.3 混合算法时间复杂度分析

算法的时间复杂度是对算法运行时间的度量，用来表示算法的计算效率的高低.算法的时间复杂度的大小在一定程度上反映了算法性能的优劣.忽略硬件及环境因素，假设每次执行时硬件条件和环境条件是完全一致的.设城市数量为n，运行迭代次数为m，则光学混沌粒子群算法的时间复杂度量级为O(m(2n2+1)).

以下来说明该算法的时间复杂度数量级为O(m(2n2+1)).根据混合算法的特点首先应用光学寻优算法初始化城市序列，并应用混沌方法生成新的城市序列，然后应用粒子群算法的核心思想不断地更新城市序列直到满足条件.

1)以一次迭代为例，城市数量为n，随机选取城市作为城市序列初始点，并应用光学寻优算法进行初始化，需要n(n－1)次运算，所以时间复杂度为O(n2－n).

2)应用混沌思想更新城市序列，对N个序列都进行更新，时间复杂度为O(n).

3)n个序列用来计算适应度函数的时间复杂度为O(n)，在此基础上进一步确定个体极值以及群体极值，计算交换子序列从而对每一个城市序列进行更新，此步骤一共运行的时间复杂度为O(n2).

4)在一次迭代完成之后判断是否达到终止条件，操作的时间复杂度为O(1).

通过以上的分析可以得出1)～4)的时间复杂度为O(2n2+1)，假设整体算法的迭代次数为m，则混合算法的整体运行时间为O(m(2n2+1)).因此整体算法的时间复杂度与城市的序列以及算法的运行代数有关，如何在保证精确度的前提下减少迭代次数也就成了控制算法运行时间的关键因素.

2.4 光学混沌粒子群算法收敛性分析

根据混沌序列的更新以及例3可得f(xi(k))是线性映射，可以写成城市序列与交换子的线性组合的形式:f(xi(k))=X(k)+βv(k).β∈［0，1］，线性系统变成如下形式:

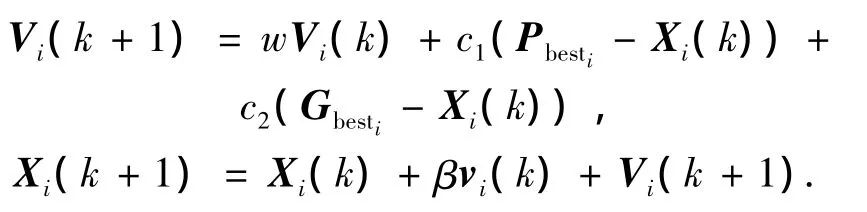
为了方便计算与分析，首先将空间简化为一维空间，将模型转化为式(5):

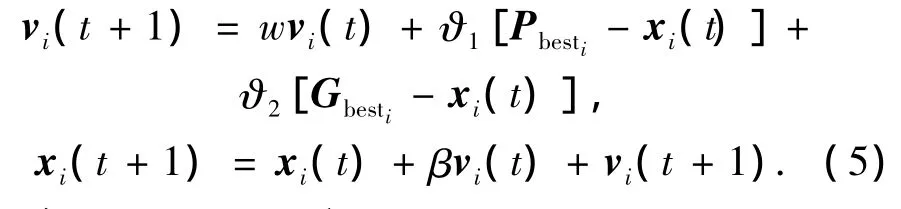
令 ϑ=ϑ1+ϑ2，记 Pbesti=pi(t)，Gbesti=pg(t)，并对模型进行简化可得表达式:

整理记为式(6):

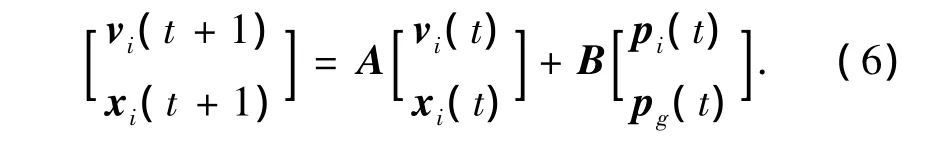
通过标准粒子群算法的数学描述可以将系统变为离散线性系统，这里假定在t次迭代之后粒子找到最优位置时，pbest、gbest将保持不变，式(6)中pi(t)、pg(t)不随着时间变化.

定理1当w＜1+β，β＜ϑ1+ϑ2＜2w+2+β时，线性定常离散系统(6)渐近稳定，并且系统收敛.

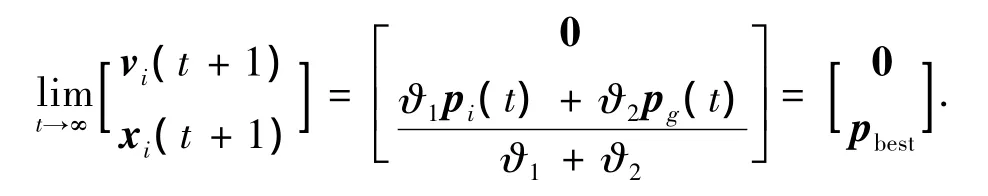
证明通过系统(6)以及模型(5)的表达式可将xi(t)消去得到如下的差分表达式:

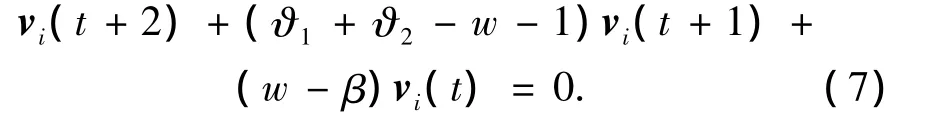
对式(7)求特征方程可得

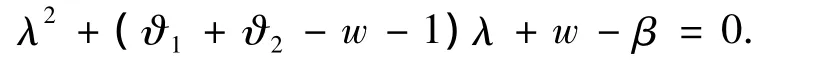
为了对式(7)进行稳定性分析，用双曲线性变换将离散系统转化为线性系统，令带入式(7)得:

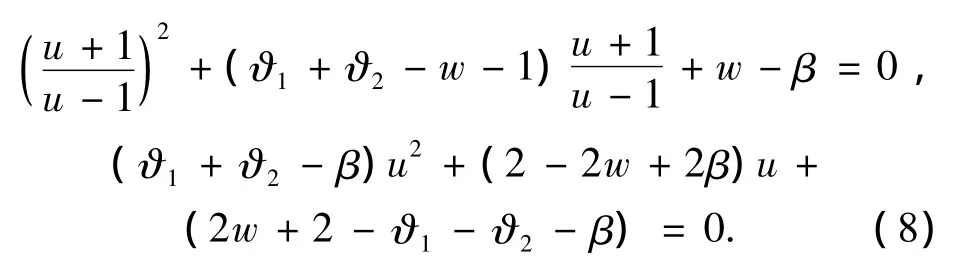
根据劳斯－赫尔维茨判据［12］，很容易得到表达式:

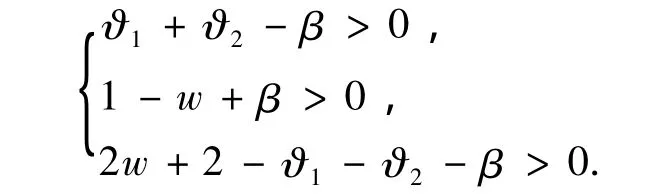
可得，当w＜1+β，β＜ϑ1+ϑ2＜2w+2+β时，线性定常离散系统(6)渐进稳定.

当系统(6)稳定，

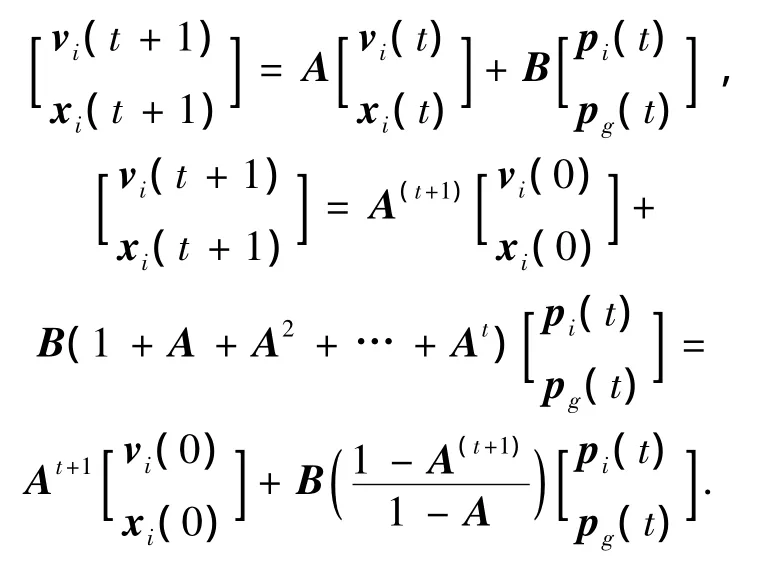
当参数满足条件(8)，|A|＜1，所以，

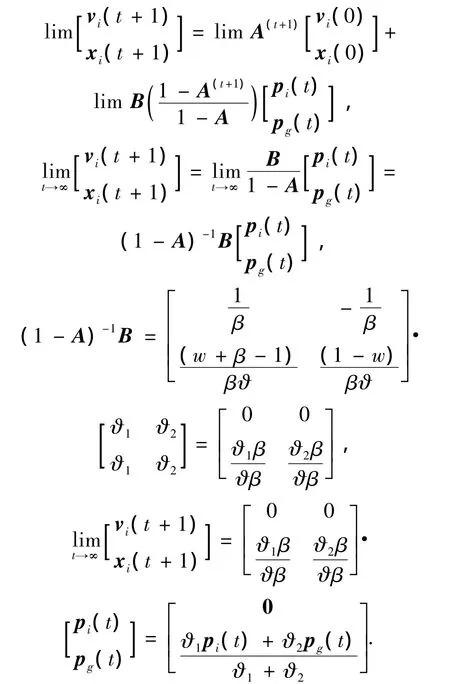
3 数值仿真

首先运用30个城市的标准TSP测试数据Oliver30对算法性能进行评估，运用蚁群算法、遗传算法、模拟退火方法、禁忌搜索方法［13］、混沌粒子群算法以及光学混沌粒子群算法，在最大迭代次数Mt=300的限定下分别对测试城市进行计算，根据定理1设定 ϑ1=0.5，ϑ2=0.5，w采用线性递减原则，t为当前的迭代次数，w=0.6 － (t/Mt)*0.5，混沌系数u=4.每种算法运行20次，对比如图6所示(X、Y的散点坐标图，取计算最好效果).各种算法计算的最好结果、最差结果以及平均迭代次数如表1所示.

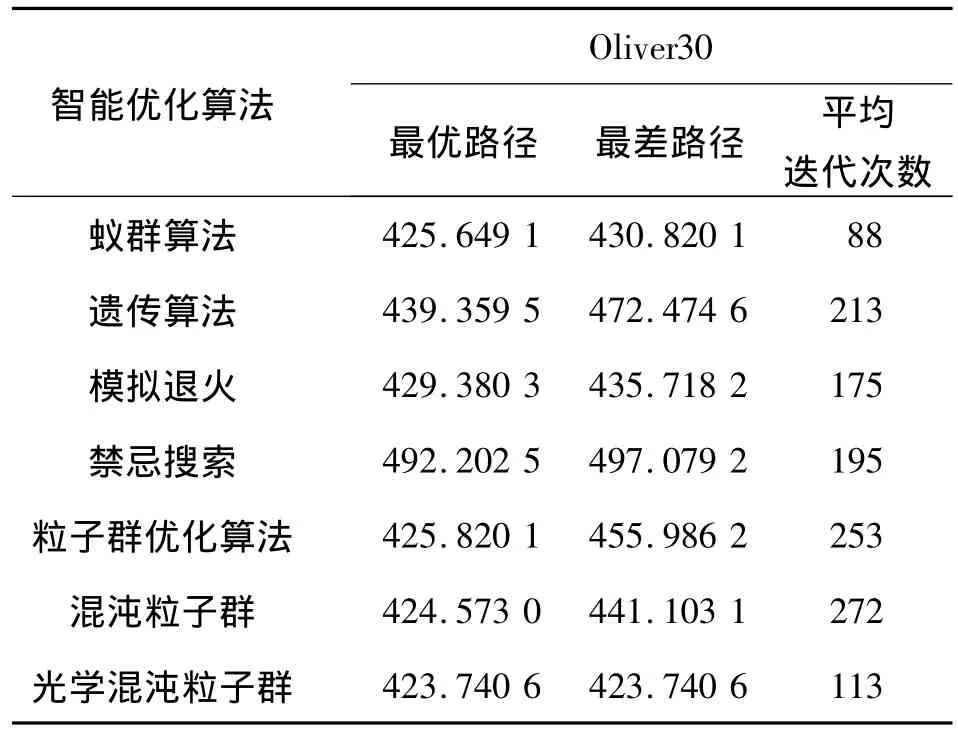
表1 对于Oliver30的算法效果对比Table 1 Algorithm contrast effects of Oliver30

从表1结果中可以看出，这4种经典智能算法精度有所差异，在有限次迭代的情况下得到的最优解效果一般，如果设置较高的迭代次数，精度能达到满意的要求，不过迭代次数较高，往往容易收敛到局部最优点.本文构建的混沌粒子群算法以及加入光学原理的混沌粒子群算法具有良好的精度，对比于基本的粒子群优化算法改进效果显著，在最大迭代次数上限为300的情况下，可以找到精确的结果，其中光学混合粒子群算法性能更为突出，每次运行都能找到最优值423.740 6.在迭代次数上，蚁群算法具有较快的收敛速度，但容易陷入局部最优点，影响算法的精度.同比与其他的5种算法，光学混沌粒子群算法在收敛速度上有很大的优势.从图7中可以看出光学混沌粒子群算法具有很强的收敛速度.

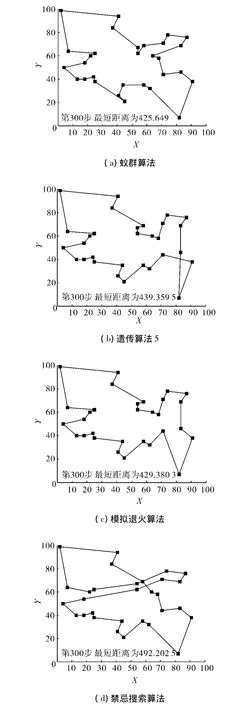
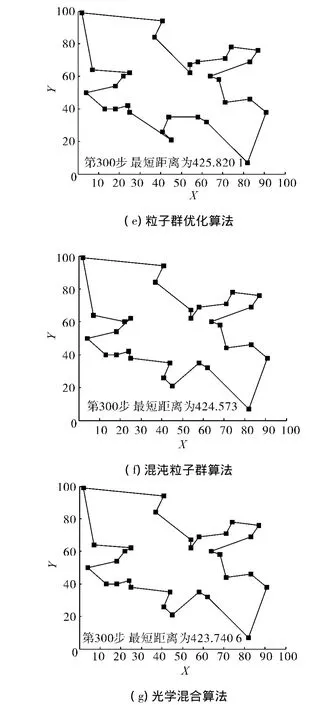
图6 7种算法Oliver30效果对比Fig.6 Seven contrast figures of Oliver30

图7 Oliver30 4种算法进化曲线Fig.7 Four evolutionary curves of Oliver30

本文提出的光学混沌粒子群算法的GUI界面如图8所示，得到的最优城市序列为(28，27，26，25，24，15，14，8，7，11，10，21，20，19，18，9，3，2，1，6，5，4，13，12，30，23，22，17，16，29)，平均迭代 113 次迭代找到最优解，混沌粒子群算法得到的最好结果为424.691 8，平均迭代次数为272，远远大于光学混沌算法，无论是迭代时间、算法精度都要劣于加入光学寻优思想的粒子群算法.光学寻优算法初始化的本质就是要减少迭代次数，提高算法精度，原因就在于用光学寻优思想形成的初始解与最优序列之间部分区域序列是相似的，甚至是完全相同的，这样在运用粒子群算法迭代时就减少了迭代次数.混沌方法具备的全局遍历性在保证算法的精度前提下，加强了算法跳出局部最优点的能力，增强了算法的适用性.

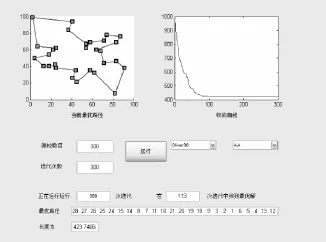
图8 光学混合算法GUI效果图Fig.8 GUI interface

表2是对测试问题eil51，参数设置与Oliver30实验相同，最大迭代次数300，每种算法计算20次所得的数据.

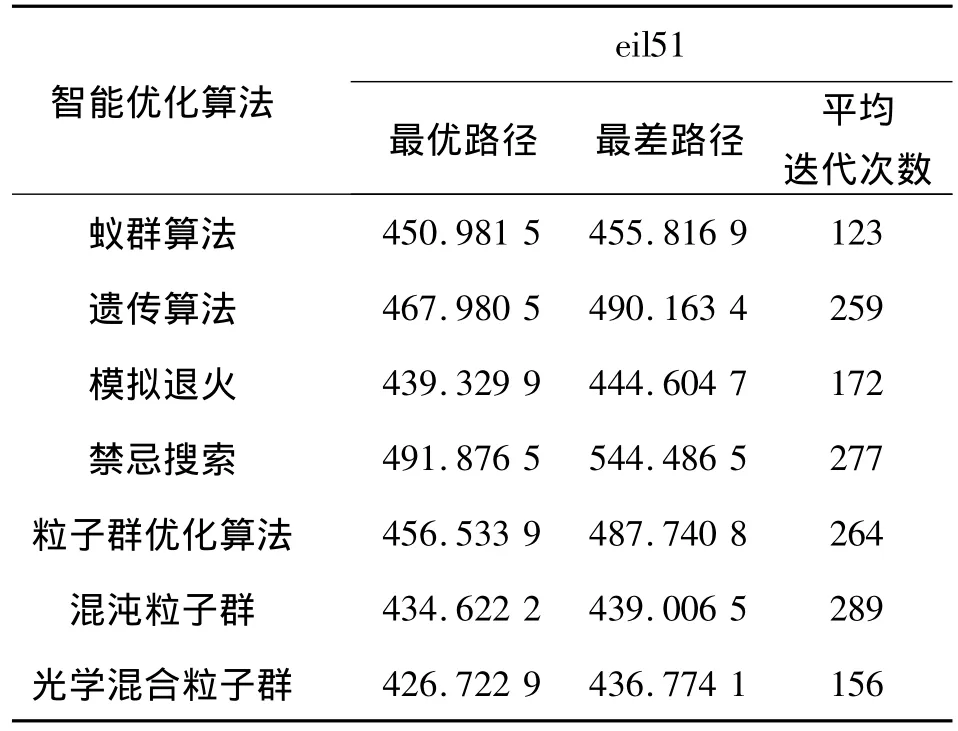
表2 对于51个城市问题eil51的算法效果对比Table 2 Algorithm contrast effects of eil51

在TSP城市规模增大的情况下，光学混沌粒子群算法的优势得到明显体现，无论是算法精度还是算法的收敛速度都要好于其他算法.从以上结果可以看出本文提出的基于光学原理的混合粒子群算法相比于其他优化算法具有良好的效果，能成功解决中大型TSP路径优化问题并保持较高的精度，加入的光学寻优思想能大大节约迭代次数，保证算法在规定的迭代次数内找到最优解.

表3是对测试问题CH130的对比数据，CH130是相对复杂的130个城市的TSP问题，最大迭代次数设定为500，每种算法运行20次，误差计算是对比于CH130给出的精确解6 110，应用最优路径计算得出，所有数据如表3所示.

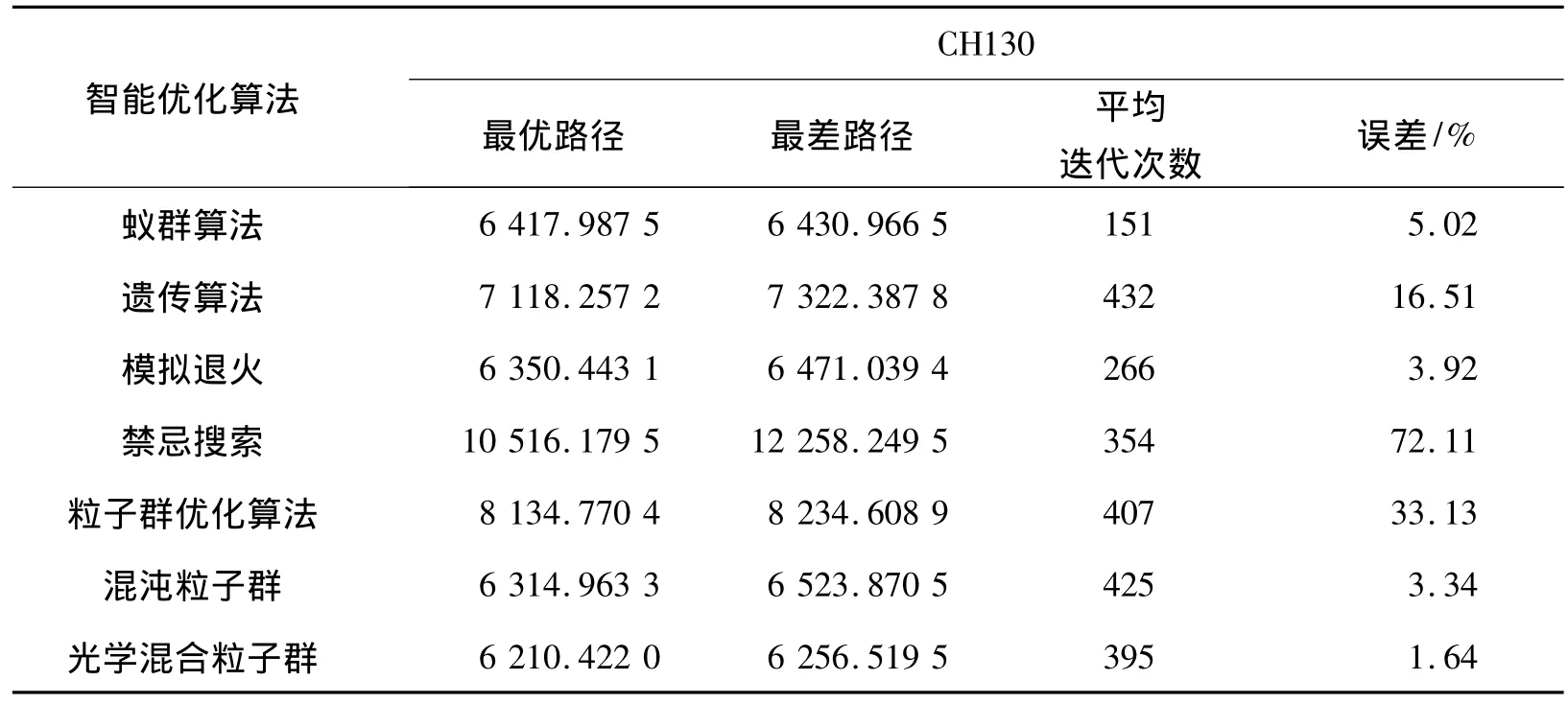
表3 对于130个城市问题CH130的算法效果对比Table 3 Algorithm contrast effects of CH130

从结果可以看出，对于较大规模的TSP问题光学混合算法效果显著，误差在所有同类算法中最低，无论是从迭代时间搜索精度，还是误差大小同比于其他算法都有很大的优势.与标准粒子群算法以及混沌粒子群算法相比，改进效果显著.图9为最优搜索形成的TSP效果图.

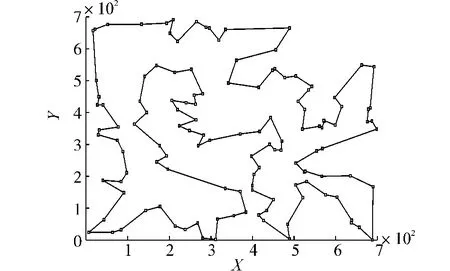
图9 应用光学混合算法求解CH130最短路径6 210.422 0Fig.9 The shortest path 6 210.422 0 of CH130 using the algorithm in this paper

4 结束语

本文提出了一种结合光学寻优算法、混沌思想的混合粒子群算法，通过光学寻优思想形成最优初值，利用加入混沌的粒子群算法成功解决了TSP问题，该算法迭代次数少、收敛速度快，对比于其他智能优化算法具有明显的优势，并用实验表明加入光学寻优思想的搜索方式大大减少了算法的迭代次数，并在一定程度上提高了算法的精度，为高效率解决大规模TSP问题提供了新的思路.

［1］KENNEDY J，EBERHART R.A discrete binary version of the particle swarm algorithm［C］//Proceedings of the World Multiconference on Systemic，Cybernetics and Informatics.Piscataway，USA:IEEE Service Center，1997:4104-4109.

［2］CLERC M.Discrete particle swarm optimization［C］//New Optimization Techniques in Engineering.Berlin:Spinger-Verlag，2004:204-219.

［3］高尚，韩斌，吴小俊，等.求解旅行商问题的混合粒子群优化算法［J］.控制与决策，2004，19(11):1286-1289.GAO Shang，HAN Bin，WU Xiaojun，et al.Solving traveling salesman problem by hybrid particle swarm optimization algorithm［J］.Control and Decision，2004，19(11):1286-1289.

［4］HENDLASS T.Preserving diversity in particle swarm optimization［J］.Lecture Notes in Artificial Intelligence，2003(2718):155-199.

［5］XIE Shenli，TANG Min，DONG Jinxiang.An improved genetic algorithm for TSP problem［J］.Computer Engineering and Application，2002，38(8):58-60.

［6］SHEN Jihong，LI Yan.Light ray optimization and its parameter analysis［C］//Proceedings of the 2009 International Joint Conference on Computational Science and Optimization.Kunming，China，2007:918-922.

［7］沈继红，李焱.基于正六边形网格的光线寻优算法［C］//中国运筹学会第十届学术交流会论文集.南京，中国，2010:89-94.SHEN Jihong，LI Yan.Light ray optimization on hexagonal grid［C］//Proceedings of the 10th ORSC.Nanjing，China，2010:89-94.

［8］SHEN Jihong，LI Jialian.The principle analysis of light ray optimization［C］//2010 Second International Conference on Computational Intelligence and Natural Computing.Wuhan，China，2010:154-157.

［9］SHI Y，EBERHART R C.A modified particle swarm optimizer［C］//Proceedings of the Congress on Evolutionary Computation.Anchorage，USA，1998:69-73.

［10］ZHANG Guoping，WANG Zhengou，YUAN Guolin.A chaotic search method for a class of combinatorial optimization problems［J］.Systems Engineering Theory ＆ Practice，2001，21(5):102-105.

［11］梁艳春，吴春国.群智能优化算法理论与应用［M］.北京:科学出版社，2009:17-21.

［12］郑大中.线性系统理论［M］.北京:清华大学出版社，2009:213-251.

［13］ANDRIES P E.计算智能导论［M］.北京:清华大学出版社，2010:111-123.