逻辑回归分析的马尔可夫毯学习算法

郭坤，王浩，姚宏亮，李俊照

(合肥工业大学计算机与信息学院，安徽 合肥 230009)

在给定贝叶斯网络(Bayesian networks)中一个变量的马尔可夫毯(Markov blanket)时，贝叶斯网络中其他变量与该变量条件独立，一个变量的马尔可夫毯能够屏蔽贝叶斯网络中其他变量对该变量的影响，可用来预测、分类和因果发现等.

确定目标变量的马尔可夫毯有2类方法:利用打分—搜索方法等建立贝叶斯网络结构，然后基于贝叶斯网络结构确定目标变量的马尔可夫毯，但该类方法得到的马尔可夫毯不准确，且学习方法效率低;另一类是利用局部学习的方法直接学习目标变量的马尔可夫毯.当前研究者主要采用基于局部学习的方法学习马尔可夫毯，相关工作如Margaritis和Thrun提出了 GS(Grow-Shrink)算法［1］，首先启发式地搜索所有与目标变量依赖的变量，然后去除冗余的变量.由于配偶节点较晚进入候选的马尔可夫毯，导致候选的马尔可夫毯中引入了较多的错误节点，降低了后面的条件独立测试的有效性和可靠性.Tsamardinos等对GS进行了改进，提出了IAMB(incremental association Markov blanket)算法［2］，每入选一个变量，就对该变量进行条件独立测试，减少了错误变量的引入;但该算法的条件独立测试是在给定整个马尔可夫毯下进行的，条件独立测试要求的数据量较大［3］.Tsamardinos等提出的 MMMB(max-min Markov blanket)算法［4］首先利用 MMPC(max-min parents and children)算法［4］寻找目标节点的父节点和子节点，然后找到它的配偶节点，但该方法会引入错误的父子节点和配偶节点［5］.与此相似的算法还有 Hiton-MB(Hiton-Markov blanket)算法［6］.Tsamardinos等在贝叶斯网络结构学习算法MMHC(maxmin Hill-climbing)［7］中调用 MMPC 算法时，利用父节点与子节点对称的性质，去除MMPC算法引入的错误父子节点.而 PCMB(parents-children Markov blanket)算法［5］利用完整的条件独立测试去除错误节点，但存在时间复杂度较大的问题.

针对上述算法存在引入错误节点和时间复杂度较大的问题，为了提高学习马尔可夫毯的精度和效率，在马尔可夫毯学习算法中引入回归分析［8］.回归分析可以在发现与目标变量相关性很强的变量的同时，去掉与目标变量相关性弱或无关的变量.回归分析广泛应用于机器学习中的特征选择，从变量集合中选取最优的特征子集［9］.根据变量数据取值是否连续，将回归分析分为线性回归分析和逻辑回归分析［10］(logistic regression analysis)2 类.逻辑回归分析可以有效处理贝叶斯网络中的离散数据.因此，如何让学习到的马尔可夫毯更加精确，学习过程效率更高，是马尔可夫毯学习算法的核心问题.提出一种基于逻辑回归分析对MMMB算法改进的RAMMMB(regression analysis-max min Markov blanket)算法.该算法对MMMB算法过程中的候选马尔可夫毯与目标变量进行逻辑回归分析，去掉相关性弱的变量，然后进行条件独立测试，去掉候选马尔可夫毯存在的兄弟节点，得到最终的马尔可夫毯.本文采用文献［11］中的G2测试来判断2个变量在给定变量集时是否条件独立，实验证明，该方法能有效地去掉MMMB算法包含的错误变量，并减少了条件独立测试的次数.

1 贝叶斯网络及相关定义

设V代表一组离散随机变量，用〈G，θ〉来表示贝叶斯网络，其中有向无环图G中的节点对应V中的变量，是指G中每个节点X在给定它的父节点Pa(X)下的条件概率分布p(X|Pa(X)).贝叶斯网络的联合概率分布可表示如下:

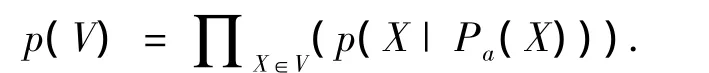
定义1 碰撞节点.如果路径P中的节点W含有2条指向它的边，那么节点W在P中是碰撞节点.在给定W时，它的2个父节点条件依赖.

定义2d分离.如果下列任意一条成立:1)路径P上存在一个包含于集合Z的非碰撞节点;2)路径P上的碰撞节点和它的子孙节点均不包含在Z中，那么称节点X到节点Y的一条路径P被节点集合Z阻塞.当且仅当从X到Y的每条路径均被Z阻塞，称节点X和Y被Z集合d分离.当有向无环图G和联合概率分布满足忠实性条件时，d分离与条件独立等价.本文中Ind(X;T|Z)表示变量T和X在给定变量集Z时条件独立;Dep(X;T|Z)表示变量T和X在给定Z时条件依赖.

定义3 马尔可夫毯.一个变量T的马尔可夫毯MB(T)是在给定该集合时，变量集V中所有其他的节点与T条件独立的最小集合.即对∀X∈V(MB(T)∪T)，Ind(X;T|MB∪T)).有向无环图G中的每个节点T，它的马尔可夫毯MB(T)包括T的父节点、子节点和配偶节点(与T共同有一个子节点).

图1中节点T的马尔可夫毯包括父节点{B，E}、子节点{C，D}和配偶节点F.

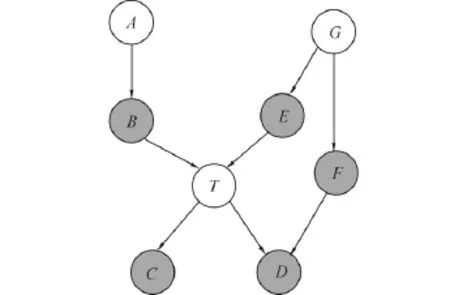
图1 T的马尔可夫毯(阴影节点)Fig.1 The Markov blanket of node T(shadow nodes)

2 MMMB算法

2.1 MMMB 算法描述

MMMB算法采用分治法发现目标变量T的马尔可夫毯MB(T)，首先调用MMPC算法找到T的父子节点集PC(T)，然后找到T的配偶节点.T的父子节点集PC(T)和配偶节点组成了T的马尔可夫毯MB(T).MMPC算法首先利用启发式搜索策略使与T相关的变量依次进入T的候选父子节点集CPC，然后移去CPC中被错误引入的变量［11］;MMMB算法对PC(T)中的每一个元素调用MMPC算法，得到T的候选马尔可夫毯CMB，经过条件独立性测试，找到T的配偶节点.然而，MMPC算法会包含未去掉的T的错误父子节点，MMMB算法也会引入T的错误的配偶节点.MMPC算法和MMMB算法描述如下.

1)MMPC算法.

2)MMMB算法描述:

2.2 MMMB算法存在的问题

MMPC算法去掉错误节点的依据为:如果X∉PC(T)，在给定Z⊆PC(T)下，X与T条件独立，通过条件独立测试可以将添加到CPC中的错误节点去掉.但存在有些错误节点不能被去掉，以图2(a)为例，节点T的父子节点集合PC(T)={A}，对T调用MMPC算法:

1)CPC添加节点.

①CPC=∅，A与T邻接，Dep(A;T|∅)的值最大，节点A首先进入到CPC;

②CPC={A}，路径T→A←B→C中的碰撞节点A包含在{A}中，该路径未被{A}阻塞，Dep(C;T|A);而Ind(B;T|∅)，节点C被添加到CPC;

③CPC={A，C}，由于 Ind(B;T|∅)，节点B不能被添加到CPC.

2)CPC={A，C}去掉错误节点.

①给定任意的集合Z，Dep(A;T|Z)，所以A不会从CPC中移除.

②由于路径T→A→C中的非碰撞节点A并不包含在∅中，该路径未被∅阻塞，Dep(C;T|∅)，且Dep(C;T|A).所以不存在CPC{C}的子集s使得Ind(C;T|s)，节点C并不能被移除，CPC={A，C}.但节点C并不在真实的PC(T)中.

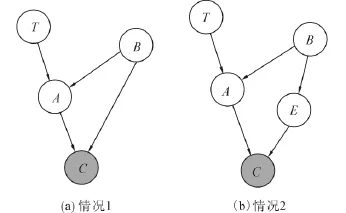
图2 MMPC算法引入错误节点CFig.2 Incorrect node C included in CPC returned MMMB算法寻找配偶节点的依据为:对X∈

同理，图2(b)中的节点C也会包含在MMPC算法输出的父子节点集合中.CMBPC(T)，Y∈PC(T)，如果存在集合Z(X，T∉Z)，且Ind(X;T|Z)，使得Dep(X;T|{Y}∪Z)，那么X为Y的配偶节点.即使MMPC算法输出的CPC为正确的PC(T)，MMMB算法返回的MB(T)也会包含错误的配偶节点.例如图3中节点T的父子节点PC(T)为{B，D}，候选马尔可夫毯 CMB={A，B，C，D}.由图 3易知Ind(A;T|{B})，路径A→C→D←T中的碰撞节点D包含在集合{D}∪{B}中，所以Dep(A;T|{D}∪{B}).A被添加到马尔可夫毯中，但是实际上A并不在节点T的马尔可夫毯MB(T)中.

图3 MMMB算法引入T的错误的配偶节点AFig.3 Incorrect spouse node A included in MMMB

MMPC算法添加的错误节点会包含在最终的马尔可夫毯MB(T)中，而且这些节点会引入T的错误的配偶节点.即使MMPC算法返回的是正确的PC(T)，MMMB本身也会引入错误的配偶节点.所以，为了提高学习马尔可夫毯算法的精度和效率，需要去掉这些错误的变量，而这些变量与目标变量的相关性不强.

3 RA-MMMB算法

3.1 根据相关性将节点分类

根据贝叶斯网络中各节点与目标节点T的相关性关系，把MMMB算法中候选马尔可夫毯CMD=PC(T)∪C∈PC(T)MMPC(C){T}中的节点分为4类:

1)T的父节点和T的子节点:这类节点与T有很强的相关性;

2)T的父节点的父节点和T的子节点的子节点:由于贝叶斯网络已存在T的父节点和T的子节点，故这类节点与T的相关性较弱;

3)T的兄弟节点(与T共同有一个父节点)和T的配偶节点:这类节点和T有共同的原因或结果，当给定T的父节点或T的子节点时，与T的相关性较强;

4)MMPC算法引入的错误节点的父子节点中上述3类以外的节点，这类节点与T的相关性最弱.

3.2 候选马尔可夫毯的逻辑回归分析

回归分析［12］可以从自变量集合中选入与因变量相关性强的自变量，并去掉那些与因变量无关的变量和与因变量相关性弱的次要变量.以目标变量T为因变量，MMMB算法中的候选马尔可夫毯CMB为自变量集合，进行回归分析，可以从CMB中去掉与目标变量相关性不强的变量.

3.2.1 候选马尔可夫毯的逻辑回归分析模型

一般贝叶斯网络中的数据为离散值，所以对目标变量和候选马尔可夫毯采用逻辑回归分析［11］.当目标变量T为0-1型(取值为2个)因变量，CMB为自变量集合时，二元逻辑回归模型为

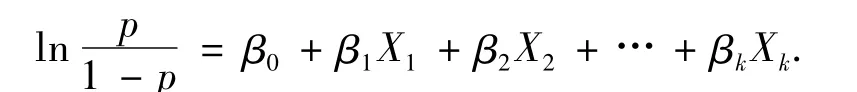
式中:p=P(T=1)，X1，X2，…，Xk∈CMB，β0，β1，…，βk为未知参数，称为回归系数.采用极大似然估计方法得到回归系数的估计值^β0，^β1，…，^βk.当因变量取值为多个(大于2个)时，采用多元逻辑回归.当目标变量T的取值有a、b、c3种，CMB为自变量集合时，多元逻辑回归的模型为:

回归分析通过假设检验判断回归系数是否为零来决定是否去掉候选马尔可夫毯中的变量.假设H0∶βi=0，i=1，2，…，k，逻辑回归中回归系数的检验统计量采用Wald统计量，即

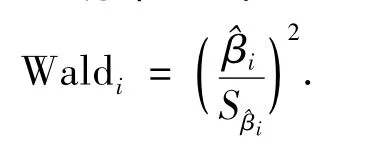
式中:S^βi为回归系数的标准误差.Wald统计量服从自由度为1的χ2分布.原假设是正确的却拒绝了该假设，犯这类错误的概率记为p.当概率值p小于给定的显著性水平α(一般取α=0.05)时，则拒绝原假设，认定该回归系数不为零;反之，认定该回归系数为零，则将该变量从方程中去掉.概率p值越小，表明对应的变量对目标变量T的影响就越显著.

3.2.2 候选马尔可夫毯的逻辑回归分析过程

采用逐步后向回归依次去掉候选马尔可夫毯CMB中与目标变量T相关性弱的变量.如果逻辑回归方程中自变量集合存在回归系数为零的概率值p大于显著性水平的变量，则将回归方程中p值最大的变量从CMB中去掉，然后建立CMB中剩余的变量与目标变量的逻辑回归方程，继续进行回归分析，再将方程中概率值p最大的变量从CMB去掉，继续回归分析直至回归方程中不再含有p值大于显著性水平的变量.

由于CMB中的第4)类节点与T的相关性最弱，所以会在逐步后向回归中最先被去掉;因为回归方程中含有T的父节点和子节点，接下来与T的相关性较弱的第2)类节点会作为回归方程中的次要变量从CMB中被去掉;第3)类节点由于T的父节点和T的子节点的存在，与T的相关性较强，所以会保留在CMB中;而第1)类节点与T的相关性最强，也包含在CMB中.

3.3 去除兄弟节点

经过逐步后向回归分析，最终的CMB中包含T的父节点和子节点、配偶节点和兄弟节点.在给定T的父节点时，T的兄弟节点与T条件独立.对于X∈CMB{PC(T)}，Y∈PC(T)，如果 Ind(X;T|Y)，则将X从CMB中去掉.而CMB{PC(T)}中不存在给定子节点时与T条件独立的变量，所以不会去掉马尔可夫毯中的变量.通过条件独立测试，去掉T的兄弟节点，得到最终的马尔可夫毯.如果PC(T)中的元素在逐步后向回归分析中被去掉，说明该元素为T的错误的父子节点，把它从候选马尔可夫毯CMB中去掉的同时，从PC(T)中也把它去掉，减少不必要的条件独立测试，并且避免在马尔可夫毯中引入其他错误的变量.

3.4RA-MMMB 算法描述

基于逻辑回归分析的马尔可夫毯学习算法RAMMMB描述如下:

RA-MMMB算法:

RA-MMMB算法运用逐步后向回归依次把MMMB算法中的候选马尔可夫毯CMB中与目标变量相关性弱的变量去掉，再经过条件独立测试，去掉兄弟节点，返回最终的马尔可夫毯.由于MMPC算法引入的错误节点是目标变量的子节点的子节点，MMMB算法引入的错误的配偶节点是目标变量的父节点的父节点，都属于上述第2)类节点，它们会在回归分析中被去掉.RA-MMMB算法的回归分析过程去掉与目标变量相关性弱的变量后，只需去掉回归分析后的CMB中的兄弟节点就能得到马尔可夫毯，与MMMB算法相比，减少了大量条件独立性测试，并且由于条件变量集很小，保证了条件独立测试的可靠性.

4 实验分析与算法比较

在Matlab 7.0和SPSS17的软件环境下，利用Insurance网(含有27个节点)和Alarm网(含有37个节点)的500、1 000、5 000组数据，对这2个网络中的每个节点分别使用MMMB算法、PCMB算法和RA-MMMB算法输出它的马尔可夫毯，并进行对比.由于实验数据为离散数据，对取值为2的目标变量，RA-MMMB算法在SPSS软件里采用二元逻辑回归，对取值为多个(大于2)的目标变量，采用多元逻辑回归.

4.1 评价标准

本文采用PCMB算法所在的文献［5］里的查准率(precision)、查全率(recall)以及它们之间的欧氏距离d来衡量马尔可夫毯学习算法的好坏.对于一个目标变量T，查准率是指算法输出的MB(T)中包含正确变量的比率;查全率是指算法输出的MB(T)中正确变量的个数占实际MB(T)变量个数的比率.

为了对上述2个标准进行综合评价，定义两者之间的欧氏距离为

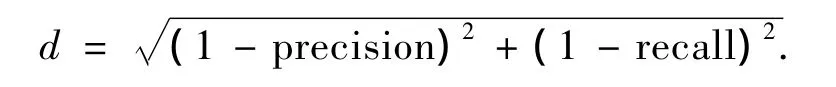
式中:d表明算法准确率，d越小，表明算法准确率越高.

4.2 分析与比较

针对Alarm网进行分析.如图4所示，图中的{X23，X22，X29，X21}和{X23，X22，X29，X1}均构成了图2(a)中的结构.节点X23的父子节点集合PC={X24，X25，X2，X22}，它的马尔可夫毯 MB={X24，X25，X2，X22，X27，X29}.当 Alarm 网中数据集大小为5 000时，利用MMPC算法得到的父子节点集合PC'={X24，X25，X2，X22，X1，X21}.比实际网络中节点X23的父子节点集合多余了X1、X21这2个节点.MMMB算法中的候选马尔可夫毯为 CMB={X24，X25，X2，X22，X1，X21，X4，X15，X19，X26，X27，X29}，最终返回的马尔可夫毯为 MB'={X24，X25，X2，X22，X27，X29，X1，X21}，比节点X23真实的马尔可夫毯多余了X1和X21这2个节点，即错误的父子节点会保留在马尔可夫毯内.

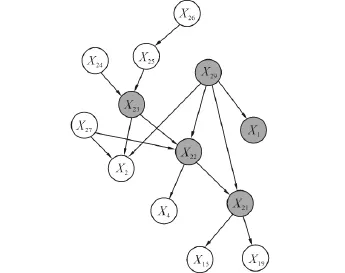
图4 Alarm网局部，阴影节点组成图2(a)的结构Fig.4 Local Alarm network，shadow nodes form the structure in Fig.2(a)

RA-MMMB算法对候选马尔可夫毯CMB与节点X23进行逐步后向回归，依次去掉了节点X15、X19、X1、X21、X4、X26，逐步后向回归去掉变量的过程如表1所示(左列的变量对应的概率值p为该变量被去掉时在回归方程中回归系数为零的概率，其余的变量对应该变量保留在最终回归方程中的p值).其中最先被去掉的2个节点X15和X19是网络中节点X21的2个子节点，而节点X21是被错误引入到节点X23的父子节点集合的节点.接着被去掉的节点X1，X21，X4是节点X23的子节点X22的子节点，节点X26是节点X23的父节点X25的父节点，剩余变量集为{X24，X25，X2，X22，X27，X29}.对回归分析后的剩余节点进行条件独立测试，发现这些均不是节点X23的兄弟节点，RA-MMMB算法返回的最终的马尔可夫毯MB″={X24，X25，X2，X22，X27，X29}，跟真实的马尔可夫毯相同，去掉了MMPC算法引入的错误的变量X1和X2.

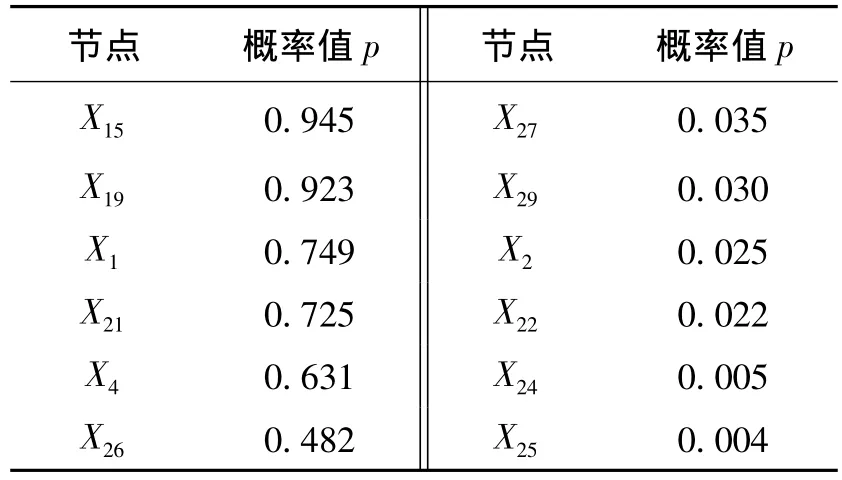
表1 节点X23和候选马尔可夫毯CMB逐步后向回归过程(显著性水平α=0.05)Table 1 The process of stepwise backward regression between node X23and CMB(significance level α=0.05)

以Alarm网中节点X19为例，如图5所示，{X29，X21，X19，X18，X28}构成了图 3 中的结构.节点X19的父子节点集 PC={X20，X21，X18}，它的马尔可夫毯MB={X20，X21，X18，X28}.当 Alarm 网中数据为5 000时，利用MMPC算法得到的父子节点集合PC'={X22，X21，X18}，与实际的父子节点集合相同.MMMB算法中的候选马尔可夫毯 CMB={X20，X21，X18，X14，X15，X22，X28，X29}，最终返回的马尔可夫毯为 MB'={X20，X21，X18，X28，X29，}，比真实的马尔可夫毯多了节点X29，即引入了节点X19的错误的配偶节点X29.

图5 Alarm网局部，阴影节点组成图3的结构Fig.5 Local Alarm network，shadow nodes form the structure in Fig.3

RA-MMMB算法对候选马尔可夫毯与节点X19进行逐步后向回归，依次去掉了节点X14、X22、X29，逐步后向回归去掉变量的过程如表2所示(左列变量含义同表1).其中节点X14为节点X19的子节点X18的子节点，节点X22和X29为节点X19的父节点X21的父节点，剩余的变量集合为{X20，X21，X18，X15，X28}.RA-MMMB算法接着通过条件独立性测试去掉了节点X15，而节点X15为网络中节点X19的兄弟节点，他们有共同的父节点X21.得到最终的 MB″={X20，X21，X18，X28}，与实际马尔可夫毯相同，去掉了MMMB算法中引入的错误的变量X29.

表2 节点X19和候选马尔可夫毯CMB逐步后向回归过程(显著性水平α=0.05)Table 2 The process of stepwise backward regression between node X19and CMB(significance level α =0.05)

对Insurance网和Alarm网里各数据集的每个节点分别使用 MMMB算法、PCMB算法和 RAMMMB算法学习它的马尔可夫毯，并计算出这3种算法对各网络的平均查准率、平均查全率和平均欧氏距离，进行比较.如图6所示.

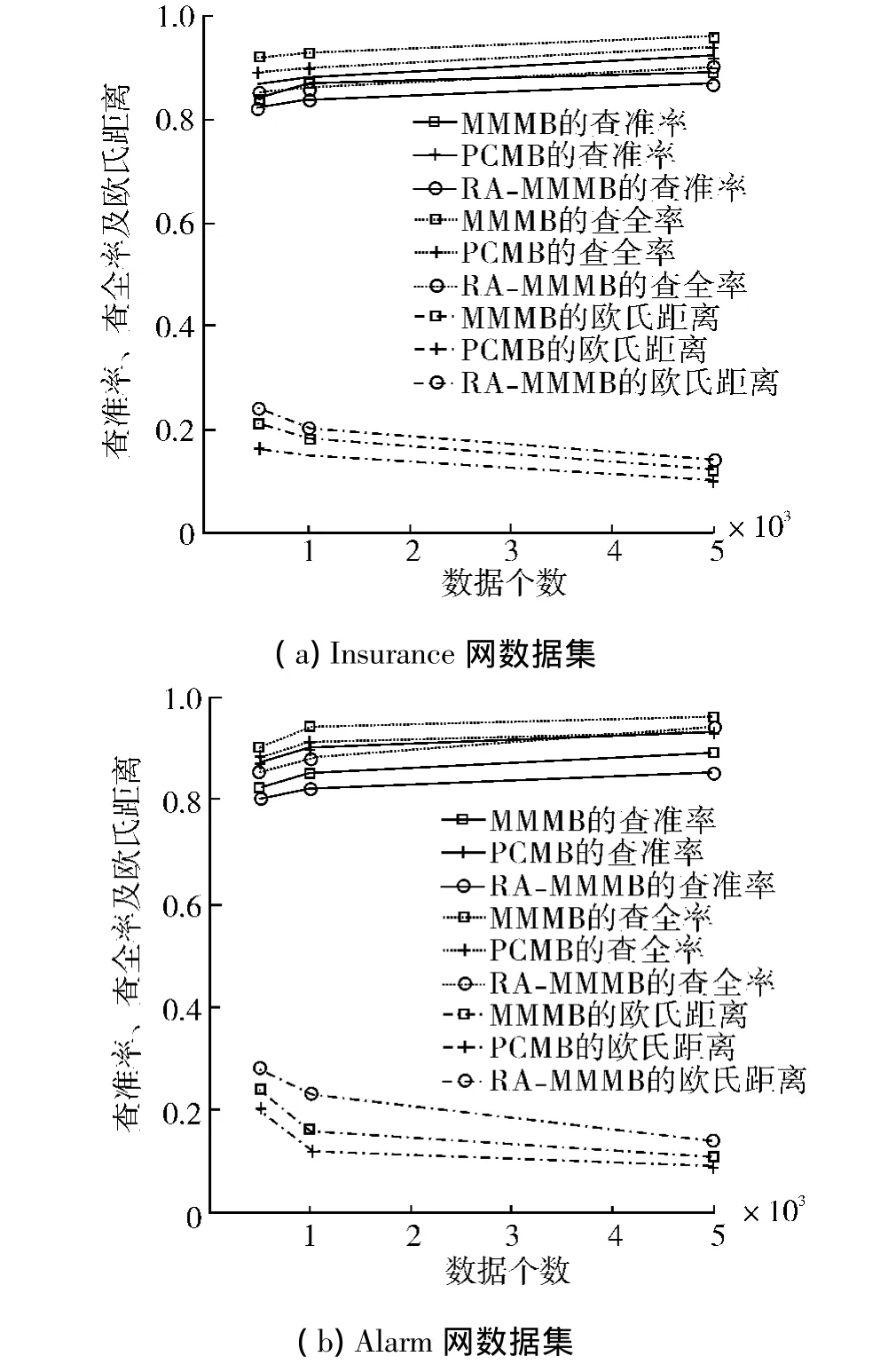
图6 Insurance和Alarm数据集各算法的查准率、查全率和欧氏距离Fig.6 Precision，recall and Euclidean distance of each algorithm in Insurance and Alarm network dataset

从图6可以看出，对不同的数据集，RA-MMMB算法输出结果的查准率、查全率均比MMMB算法的结果高，相应的欧氏距离均比MMMB算法小，表明了该算法要优于MMMB算法;而与PCMB算法相比，虽然RA-MMMB算法查全率偏低，但查准率较高，综合评价指标欧氏距离小，体现了在整体上要优于PCMB算法.同时可以看出，数据集中样本数目越多，欧氏距离就越小，算法的准确率就越高.

5 结束语

基于逻辑回归分析的马尔可夫毯学习算法，对MMMB算法里存在错误的父子节点和配偶节点的问题进行了分析，然后对MMMB算法中的候选马尔可夫毯与目标变量进行逐步后向回归，去掉了错误节点和其他与目标变量相关性弱的节点，然后进行条件独立测试去掉兄弟节点，减少了条件独立测试的次数，提高了学习马尔可夫毯的精度.针对本算法的查全率较PCMB算法低的缺点，需要进一步的工作去改进.

［1］MARGARITIS D，THRUN S.Bayesian network induction via local neighborhoods［C］//Advances in Neural Information Processing Systems.Denver，Colorado，USA，1999:505-511.

［2］TSAMARDINOS I，ALIFERIS C F，STATNIKOV A.Algorithms for large scale Markov blanket discovery［C］//Proceedings of the Sixteenth International Florida Artificial Intelligence Research Society Conference.St Augustine，Florida，USA，2003:376-380.

［3］FU Shunkai，Desmarais M C.Markov blanket based feature selection:a review of past decade［C］//Proceedings of the World Congress on Engineering London，UK，2010:22-27.

［4］TSAMARDINOS I，ALIFERIS C F，STATNIKOV A.Time and sample efficient discovery of Markov blankets and direct causal relations［C］//Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Washington，DC，USA，2003:673-678.

［5］PE~NA J M，NILSSON R，BJRKEGREN J，et al.Towards scalable and data efficient learning of Markov boundaries［J］.International Journal of Approximate Reasoning，2007，45(2):211-232.

［6］ALIFERIS C F，TSAMARDINOS I，STATNIKOV A.HITON:a novel Markov blanket algorithm for optimal variable selection［C］//Proceedings of the 2003 American Medical Informatics Association Annual Symposium.Washington，DC，USA，2003:21-25.

［7］TSAMARDINOS I，BROWN L E，ALIFERIS C F.Themax-min hill-climbing Bayesian network structure learning algorithm［J］.Machine Learning，2006，65:31-78.

［8］孟晓东，袁道华，施惠丰.基于回归模型的数据挖掘研究［J］.计算机与现代化，2010，173(1):26-28.MENG Xiaodong，YUAN Daohua，SHI Huifeng.Research on regress-base system on data mining［J］.Computer and Modernization，2010，173(1):26-28.

［9］SINGH S，KUBICA J，LARSEN S，et al.Parallel large scale feature selection for logistic regression［C］//SIAM International Conference on Data Mining(SDM).Sparks，Nevada，USA，2009:1171-1182.

［10］施朝健，张明铭.Logistic回归模型分析［J］.计算机辅助工程，2005，14(3):74-78.SHI Chaojian，ZHANG Mingming.Analysis of logistic regression models［J］.Computer Aided Engineering，2005，14(3):74-78.

［11］高晓光，赵欢欢，任佳.基于蚁群优化的贝叶斯网络学习［J］.系统工程与电子技术，2010，32(7):1509-1512.

［12］SPIRTES P，GLYMOUR C，SCHEINES R.Causation，prediction，and search［M］.2nd ed.Cambrdge，USA:The MIT Press，2000:23-28.GAO Xiaoguang，ZHAO Huanhuan，REN Jia.Bayesian network learning on algorithm based on ant colony optimization［J］.Systems Engineering and Electronics，2010，32(7):1509-1512.