TSNAM彩色图像的格雷码表示

郑运平，张佳婧

(华南理工大学计算机科学与工程学院，广东 广州 510006)

布局问题包含了种类繁多的若干类问题如三角形布局问题、矩形布局问题和装箱问题等，这些问题在许多领域里能够得到广泛的应用，有着巨大的理论价值和实际意义［1-2］.在Internet已成为最主要的信息传输途径的今天，由于图像信息所具有的大量性，其快速、实时传输的要求得不到满足，已成为制约Internet发展的一个难题.许多实际的应用由于大量的图像信息得不到快速传输而使系统的实时效果不是很理想.因此图像表示方法的研究就变得非常重要，它是目前最活跃的研究领域之一［3-5］.四元树(linear quadtree，LQT)表示是研究得最早、最多的一种图像表示方法［6］.为了进一步减少存储空间，Gargantini消除了指针方案，提出了线性四元树表示方法［7］.一般情况下，LQT表示方法可节省66%的存储空间;特殊情况下，可节省高于90%的存储空间.借助于矩形布局问题的思想，通过使用位平面分解方法，文献［8］提出了一种基于非对称逆布局的模式表示模型(non-symmetry and anti-packing pattern representation model，NAM)的彩色图像表示方法，这是彩色图像的间接矩形NAM表示方法.随后，文献［9］提出了彩色图像的直接矩形NAM表示方法.文献［8-9］中用到的子模式均为矩形，对于具有块状性的图像具有较好的表示效果.对于块状性不好或者没有明显块状性的图像，三角形子模式是一个很好的选择，鉴于此，笔者在文献［10］中曾提出了灰度图像的直接三角形NAM表示方法，而在文献［11］中提出了灰度图像的间接三角形NAM表示方法(IITNAM).最近，借助三角形和正方形布局问题的思想，通过在IITNAM表示方法中增加正方形子模式，文献［12］提出了一种称为TSNAM的图像表示方法，并且也使用了BPD方法.尽管BPD方法是一种有效降低图像复杂度的方法，但采用这种方法来分解位平面存在一个缺点，即像素点灰度值的微小变化会对位平面的复杂度产生较明显的影响.例如，当空间相邻的2个像素的灰度值分别为127=(01111111)2和128=(10000000)2时，图像的每个位平面在这个位置处都会有从0到1(或从1到0)的传输，而由法国工程师 J.M.E.Baudot于1880年发明的格雷码(Gray code)则没有这一缺点，格雷码在任意2个相邻的数之间转换时，只有一个数位发生变，它大大地减少了由一个状态到下一个状态时逻辑的混淆.

因此，为了进一步提高TSNAM的表示效率，同时也为了减小像素点灰度值的微小变化会对位平面的复杂度产生较明显的影响，本文将格雷码和BPD方法应用到彩色图像的TSNAM表示方法中，提出了一种基于格雷码的TSNAM彩色图像表示方法(GTSNAM).理论分析和实验结果表明了本文提出的GTSNAM表示方法的正确性和有效性.

1 彩色图像的GTSNAM方法

1.1 TSNAM方法的思想

在TSNAM表示方法中，预先定义的子模式集合是三角形和正方形.其中，将三角形子模式分成了4类:上三角形、下三角形、对称上三角形和对称下三角形.这样，对于任何一个三角形子模式，不需要存储3个顶点的坐标，而只要存储斜边的2个端点和一个用于标识三角形子模式类型的标识符(比如上三角形、下三角形、对称上三角形和对称下三角形分别用“0”、“1”、“2”和“3”这4个数来标识)即可.相反，以斜边的2个端点和三角形类型的标识符，也可以非常简单地解码出三角形子模式.

彩色图像的TSNAM表示方法的主要思想是:对一幅彩色图像，首先获取其3幅由r、g、b颜色分量组成的灰度图像，然后通过BPD方法对每幅灰度图像进行分解，获得相应的位平面二值图像，最后用三角形和正方形子模式对所有二值图像进行逆布局.事实上，TSNAM表示方法对IITNAM表示方法的改进主要体现在TSNAM表示方法中新增了一个正方形子模式.

1.2 彩色图像的GTSNAM算法描述

设已经布局好的彩色图像模式为C，位深为m，大小为2n×2n×3，其分解后的3幅灰度图像模式为G［1］、G［2］和G［3］，大小均为 2n×2n.为方便起见，假定“0”为“black”，即黑色，表示区域，“1”为“white”，即白色，表示背景点.本算法只需记录“black”像素点.GTSNAM表示算法中被逆布局的子模式对象是任意大小的三角形和正方形，其中三角形子模式t={triangle|triangle=(flag，point1_hyp，point2_hyp)}，flag占2 bit，flag=0时表示上三角形，flag=1时表示下三角形，flag=2时表示对称上三角形，flag=4时表示对称下三角形;point1_hyp和point2_hyp表示斜边的2个端点;且正方形子模式s={square|square=(sp，edge)}中，sp和 edge分别代表正方形左上角的坐标及边长.

以下给出了GTSNAM表示算法的具体步骤:

输入:一幅2n×2n×3的彩色图像模式C以及其位深m.

输出:Q={Qt，Qs，Ql，Qp}，Qt={Qt0，Qt1，…，Qt3m－1}，Qs={Qs0，Qs1，…，Qs3m－1}，Ql={Ql0，Ql1，…，Ql3m－1}和Qp={Qp0，Qp1，…，Qp3m－1}.其中Qti、Qsi、Qli和Qpi(0≤i≤3m－ 1)分别表示第i个格雷码位面图CPi的三角形、正方形、线段和孤立点的编码结果.

1)对于一个给定的大小为2n×2n×3的彩色图像C，分别取得由它的r、g、b颜色分量组成大小为2n×2n的灰度图像G［1］、G［2］和G［3］，并把三角形、正方形、线段和孤立点的计数变量tn、sn、ln和pn均赋值为0.

2)用灰度图像的BPD方法依次将3幅灰度图像G［1］、G［2］和G［3］各自分解为m幅二值图像BPi(0≤i≤m－1)、BPi(m≤i≤2m－1)和 BPi(2m≤i≤3m－1).

3)当k=1，2，3 时，根据式(1)，依次计算出每m幅二值位面图 BPi(0≤i≤m－1)、BPi(m≤i≤2m－1)和BPi(2m≤i≤3m－1)所分别对应的m幅格雷码位面图CPi(0≤i≤m－1)，CPi(m≤i≤2m－1)和 CPi(2m≤i≤3m－1)，并令j=0.

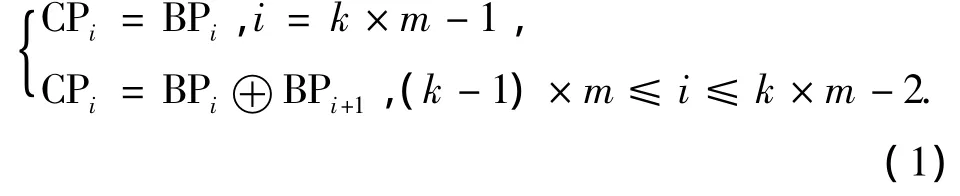
4)从CPj的第1个入口开始，首先用光栅扫描的方法确定一个未被标识的起始点(x，y)，再根据三角形子模式的匹配(逆布局)策略来尽可能地形成最大的三角形子模式.

5)如果以(x，y)为端点找到的最大三角形子模式为上三角形(或对称上三角形)，则将flag赋为0(或2)，三角形的计数变量tn的值加1，且将这个三角形子模式作标识.

6)记录斜边端点的2个坐标(x1，y1)和(x2，y2)，然后对斜边的2个端点作K码降维变换，即point1_hyp←K(x1，y1)，point2_hyp←K(x2，y2)，最后将flag、point1_hyp、point2_hyp这3个变量存储到队列Qtj中，即有Qtj{tn}←{flag，point1_hyp，point2_hyp}.

7)如果以(x，y)为端点找到的最大三角形子模式为下三角形(或对称下三角形)，则将flag赋为1(或3)，三角形的计数变量tn的值加1，且将这个三角形子模式作标识，记录斜边端点的2个坐标(x1，y1)和(x2，y2)，然后对斜边的2个端点作K码降维变换，即:point1_hyp←K(x1，y1)，point2_hyp←K(x2，y2)，最后将 flag、point1_hyp、point2_hyp 这 3 个变量存储到队列Qtj中，即有Qtj{tn}←{flag，point1_hyp，point2_hyp}.

8)如果以(x，y)为端点找到的最大上三角形(或对称上三角形)子模式的面积和最大下三角形(或对称下三角形)子模式的面积相等，且这2个三角形能构成一个正方形，则将tn的值减2，同时将sn的值加1.

9)记录此最大正方形子模式的2个参数，即起始点坐标(x，y)和边长edge;然后对起始点坐标(x，y)作K码降维变换，即 sp←K(x，y);最后将sp和edge这2个变量存储到队列Qsj中，即有Qsj{sn}←{sp，edge}，并将此正方形在CPj中作标识.

10)循环执行4)～9)，直到不能形成新的三角形和正方形子模式为止.

11)按光栅扫描的顺序，从标记过的CPj的第1个入口开始，首先确定1个未被标记的点，再根据子模式的匹配(逆布局)算法来尽可能地形成最长的线段，如果能形成线段，则将线段的计数变量ln的值加1，记录线段端点的2个坐标(x1，y1)和(x2，y2)，然后对线段的2个端点作K码降维变换，即l1←K(x1，y1)，l2←K(x2，y2).最后将l1和l2这 2 个变量存储到队列Qlj中，即有Qlj{ln}={l1，l2}，且将存储过的此线段在CPj中作标识.否则，说明只能形成孤立点，执行12).

12)直接存储孤立点的坐标(x，y)，将孤立点的计数变量pn的值加1，然后将这个点作K码降维变换，即p←K(x，y).最后将p这个变量存储到队列Qpj中，即有Qpj{pn}={p}，并将此点在CPj中作标识.

13)循环执行11)～12)，直到不能形成新的线段和孤立点为止.

14)j=j+1.若j≤3m－1，则执行4).

15)输出编码结果Q={Qt，Qs，Ql，Qp}，其中Qt= {Qt0，Qt1，…，Qt3m－1}，Qs= {Qs0，Qs1，…，Qs3m－1}，Ql={Ql0，Ql1，…，Ql3m－1}和Qp= {Qp0，Qp1，…，Qp3m－1}.

1.3 算法复杂度分析

假定彩色图像C中元素的总数为N，多子模式的类型数为n，位深为m.由于采用了BPD方法，一幅彩色图像被分解为3m幅二值图像来处理，因此，对GTSNAM算法来说，编码所需的时间正比于mnNτ，其中τ表示图像中每个像素平均分割的次数，且τ的上限为O(lbN).因此，在最坏情况，编码算法时间复杂度为O(mnN×lbN).

在空间开销方面，编码算法除3m幅二值图像矩阵外，只增加了为数非常少的中间变量，因而其空间复杂度与3m幅二值图像的大小成正比，即为O(mN).

2 GTSNAM表示的存储结构和数据量

2.1 GTSNAM表示的存储结构分析

从GTSNAM表示算法不难看出，彩色图像模式的编码结果为队列集合Q={Qt，Qs，Ql，Qp}，Qt={Qt0，Qt1，…，Qt3m－1}，Qs={Qs0，Qs1，…，Qs3m－1}，Ql={Ql0，Ql1，…，Ql3m－1}和Qp={Qp0，Qp1，…，Qp3m－1}.其中Qti、Qsi、Qli和Qpi(0≤i≤3m－ 1)分别表示第i个格雷码位面图CPi的三角形、正方形、线段和孤立点的编码结果.Qti所存储的每一条记录均为一个三角形子模式，且有3个参数，即t={triangle|triangle=(flag，point1_hyp，point2_hyp)};Qsi所存储的每一条记录均为一个正方形子模式，且有2个参数，即s={square|square=(sp，edge)}.因此，三角形和正方形子模式的存储结构分别如图1和图2所示.

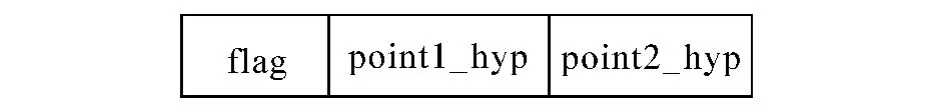
图1 三角形子模式的存储结构Fig.1 Storage structure of a triangle subpattern

图2 正方形子模式的存储结构Fig.2 Storage structure of a square subpattern

就正方形子模式而言，设给定的彩色图像模式C大小为2n×2n×3，从文献［12］的分析可知:sp即为一个坐标对(x，y)，x和y的二进制码长度都为n.具体存储记录用K码表示.K用相对值来记录，本次记录的K域用本次K码减去上一个K码的差值来记录，即 ΔK=Ki－Ki－1.在统计意义下其长度为n，在实际情况下，如果ΔK的长度确实超过了n，则可以将该块拆分为2个块，用2个记录来表示.子模式的表示只有1个值，即边长edge.按照K的定义，edge的最大长度为n.因此，存储一个正方形子模式长度为2n.

通过类似的分析，易知存储一个三角形、线段和孤立点记录长度分别为2n+2、2n和nbit.

2.2 GTSNAM表示的数据量分析

设彩色图像模式C的大小为2n×2n×3，位深为m，经彩色图像的BPD后，可以将其分解为3幅大小为2n×2n的灰度图像模式或者3m幅大小为2n×2n的二值图像模式.令第i个色彩分量的第j个格雷码位面图逆布局后的三角形、正方形、线段、孤立点的子模式数分别为Mt(i，j)、Ms(i，j)、Ml(i，j)和Mp(i，j)，其中 1≤i≤3，且 0≤j≤m－1.

就GTSNAM表示方法而言，存储一个三角形、正方形、线段和孤立点记录分别占2n+2、2n、2n和n.因此，C用GTSNAM表示方法逆布局后的3m幅格雷码位面图的总数据量TGTSNAM为

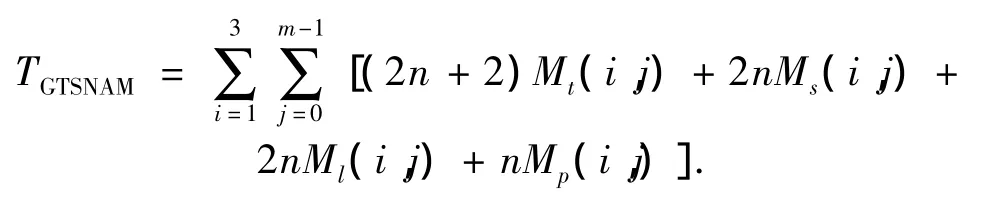
对于LQT表示方法来说，存贮一个节点占3n－1+m［10］，设NLQT(i)表示第i个色彩分量，用 LQT 表示的总节点数，则LQT的总数据量TLQT为

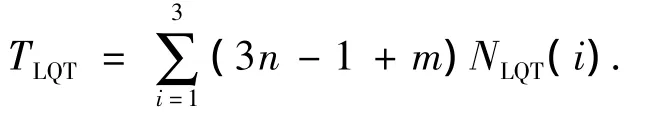
令β为LQT的总数据量与GTSNAM的总数据量的比值，则有

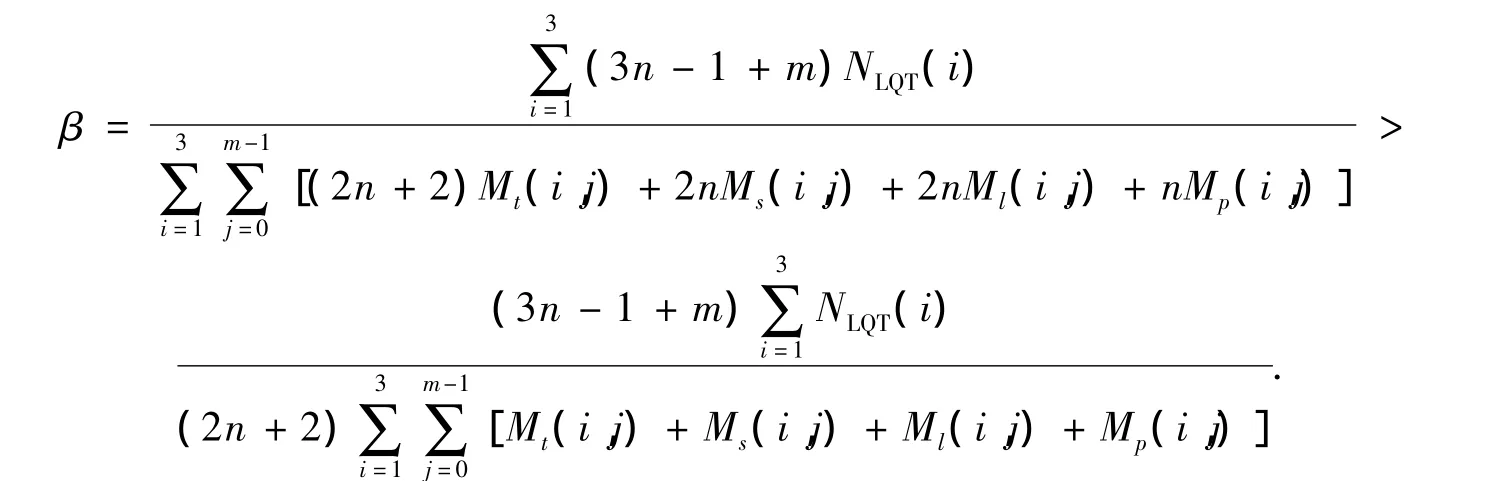
通过β这一比值，可以比较GTSNAM相对于LQT的优劣.由于LQT表示是对称分割，分割方法受到很大限制，而GTSNAM表示是非对称分割，其分割方法更为灵活，且其目的是产生尽可能少的子模式数，因此，

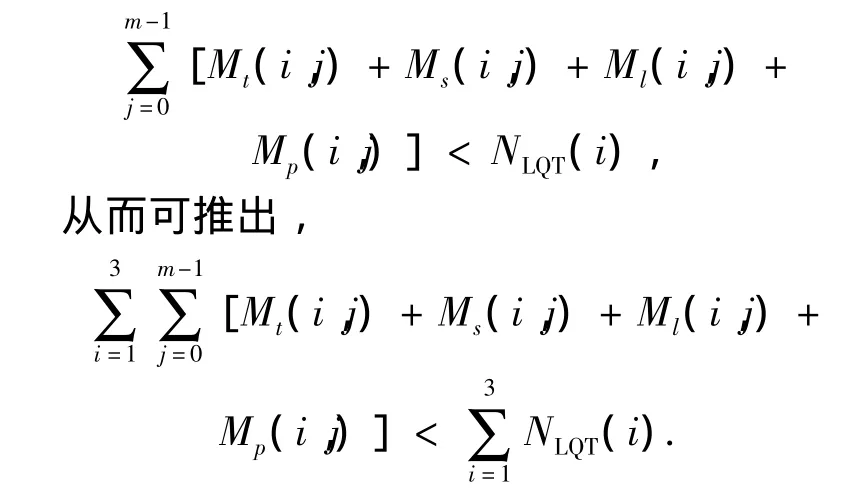
因此β＞(3n－1+m)/(2n+2)＞1.比如在实验中，当n=9，m=8 时，从理论上来说，β ＞1.7 ＞1.

综上所述，理论分析表明，对彩色图像模式而言，与经典的LQT表示方法相比，GTSNAM表示方法能够更有效地减少数据存储空间.

3 实验与分析

为了验证彩色图像的GTSNAM表示方法的理论结果，本节从实验的角度来说明其相对于无格雷码的TSNAM表示方法和经典的LQT表示方法的明显优势.实验中机器配置为:CPU为Celeron(R)2.4 GHz，内存为 Kingston DDR 2GB，OS 为 MS-Windows XP Service Pack 2.编程环境为 Matlab 7.0.图3 是实验中用来测试的4幅彩色图像，其中图3(a)、(b)是2幅机器人图像，图3(c)、(d)是2幅图像处理领域里惯用的标准图像“Flight”和“Lena”，且这些图像的分辨率参数n=9，即29×29×3的彩色图像模式，位深m=8，即28=256级.

图3 4幅彩色图像Fig.3 Four color images

通过编程，分别实现了彩色图像的GTSNAM、TSNAM、及LQT表示算法，并对这3种算法的实验结果进行了比较，相应的比较数据如表1所示，其中:N为子模式或节点个数，TSNAM为无格雷码的TSNAM表示，GTSNAM为基于格雷码的TSNAM表示，LQT为线性四元树表示，δ为TSNAM与GTSNAM的子模式数之差，α为LQT与TSNAM的总数据量之比，β为LQT与GTSNAM的总数据量之比.图4给出了LQT、TSNAM和GTSNAM表示方法的子模式数或结点数的对比.

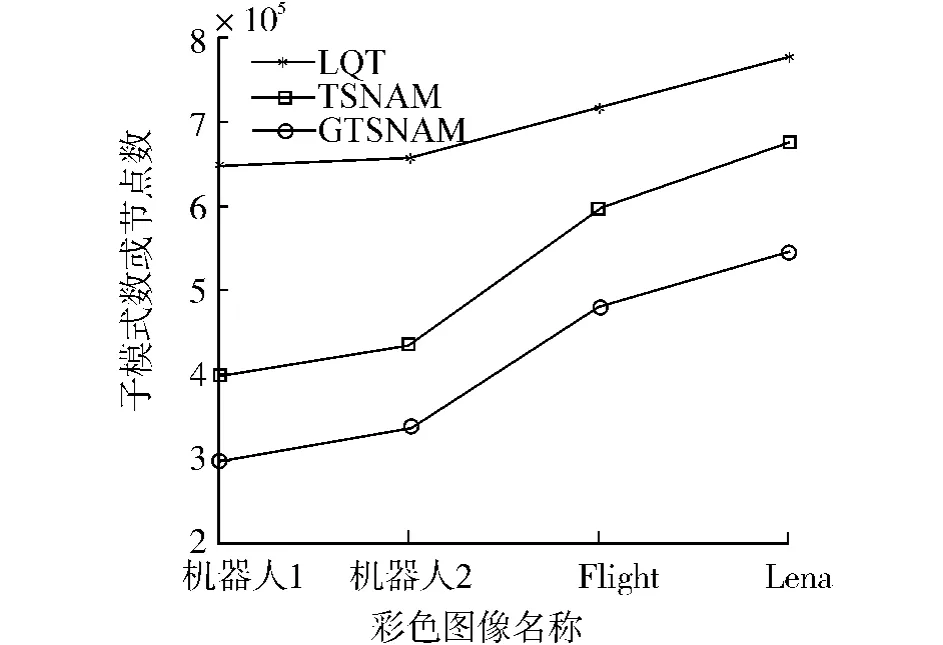
图4 LQT、TSNAM和GTSNAM的子模式数或节点数的对比Fig.4 Contrast of the subpattern or node number among the LQT，TSNAM，and GTSNAM

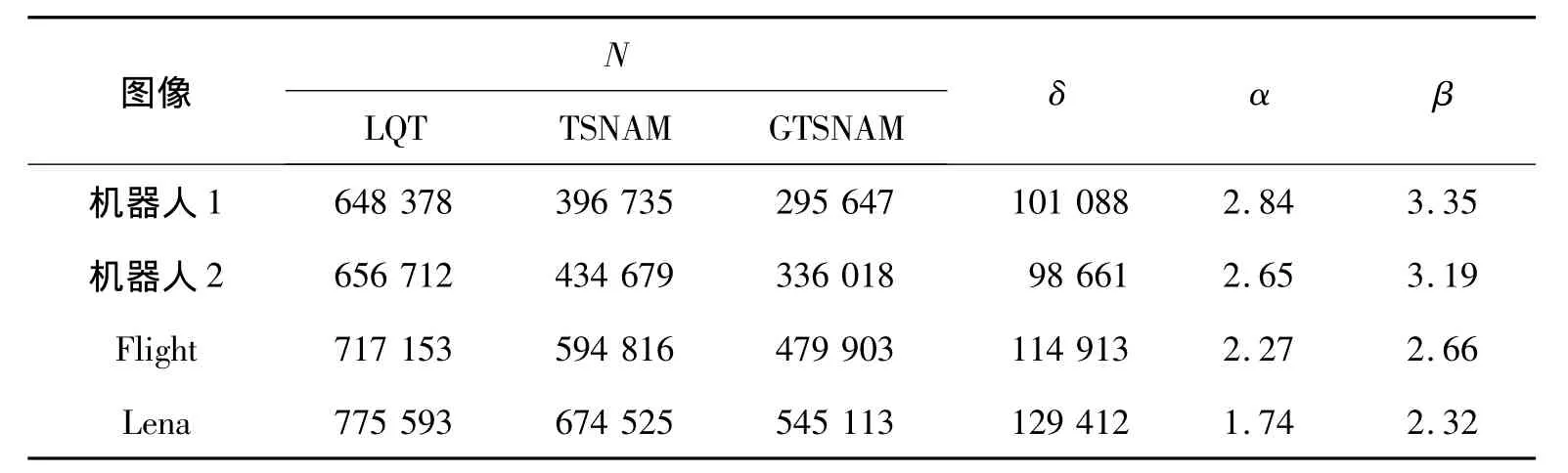
表1 LQT、TSNAM和GTSNAM的性能比较Table 1 Performance comparison among the LQT，TSNAM，and GTSNAM

从图4中实验数据N来看，TSNAM和GTSNAM在数据量方面的效果均是非常明显的，其子模式数均小于LQT方法的节点数.而且从表1中δ的值可知，GTSNAM的子模式数比TSNAM的子模式还要少98 661～129 412个，同时，从表1中N的值不难算出，在子模式数上 GTSNAM比TSNAM下降了16.71% ～25.48%，效果是非常显著的.因此，与LQT和TSNAM方法相比，GTSNAM方法能够更有效地减少子模式的数量.而且，从β值不难看出，对于给定的4幅图像而言，LQT的总数据量是GTSNAM的2.32～3.35倍，显然，这些图像均证实了理论分析的结果，即当n=9，m=8 时，β ＞1.7 ＞1.并且从表1也不难看出，β总是大于α，这表明，在数据存储表示方面，GTSNAM能够比LQT和TSNAM方法更有效地减少数据存储空间.

因此，与LQT和TSNAM表示方法相比，GTSNAM方法能够更有效地减少子模式数(节点数)和数据存储空间.

4 结束语

位平面分解方法是一种有效降低图像复杂度的方法.为了进一步提高TSNAM的表示效率，同时也为了减小像素点灰度值的微小变化会对位平面的复杂度产生较明显的影响，本文将格雷码和位平面分解方法应用到彩色图像的TSNAM表示方法中，提出了一种基于格雷码的TSNAM彩色图像表示方法(GTSNAM).给出了GTSNAM算法的形式化描述，并对其存储结构、总数据量和时空复杂性进行了详细的分析.理论分析和实验结果表明，与最新提出的TSNAM表示方法和经典的LQT表示方法相比，GTSNAM表示方法具有更少的子模式数(或节点数)，能够更有效地减少数据存储空间，因而是一种有效的彩色图像表示方法.

［1］CHEN Chuanbo，HE Dahua.Heuristic method for solving triangle packing problem［J］.Journal of Zhejiang University:Science，2005，6(6):565-570.

［2］CHEN T G，RYCKELYNCK P.Improved dense packings of congruent squares in a square［J］.Discrete Comput Geom，2005，34(1):97-109.

［3］DAI D，YANG W.Satellite image classification via two-layer sparse coding with biased image representation［J］.IEEE Geoscience and Remote Sensing Letters，2011，8(1):173-176.

［4］ZHENG Yunping，SAREM M.A fast algorithm for computing moments of gray images based on NAM and extended shading approach［J］.Frontiers of Computer Science in China，2011，5(1):57-65.

［5］YAP P，JIANG X，KOT A C.Two-dimensional polar harmonic transforms for invariant image representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(7):1259-1270.

［6］KLINGER A.Data structure and pattern recognition［C］//Proc of First International Joint Conference on Pattern Recognition.Washington DC，USA，1973:497-498.

［7］GARGANTINI I.An effective way to represent quadtrees［J］.Communications of the ACM，1982，25(12):905-910.

［8］郑运平，陈传波.一种基于非对称逆布局模型的彩色图像表示方法［J］.软件学报，2007，18(11):2932-2941.ZHENG Yunping，CHEN Chuanbo.A color image representation method based on non-symmetry and anti-packing model［J］.Journal of Software，2007，18(11):2932-2941.

［9］CHEN C B，ZHENG Y P，SAREM M.A direct non-symmetry and anti-packing model for color image［C］//Proc of the 4rd International Conference on Natural Computation and the 5th International Conference on Fuzzy Systems and Knowledge Discovery.Los Alamitos，USA，2008:347-351.

［10］ZHENG Y P，CHEN C B，SAREM M.A novel algorithm for triangle non-symmetry and anti-packing pattern representation model of gray images［C］//Proc of the 3rd International Conference on Intelligent Computing.Berlin，Germany，2007:832-841.

［11］ZHENG Y P，GUO X.An improved indirect triangle nonsymmetry and anti-packing model for gray image representation［C］//Proc of the 2011 International Conference on Multimedia and Signal Processing.Los Alamitos，USA，2011:117-121.

［12］ZHENG Y P，LI Z J，SAREM M，et al.A new IITNAM representation method of gray images［C］//Proc of the 8th International Conference on Fuzzy Systems and Knowledge Discovery.Los Alamitos，USA，2011:1897-1901.