可燃介质中飞行圆球诱导斜爆轰的流场结构＊

周 平，范宝春，归明月

（1.南京理工大学瞬态物理国家重点实验室，江苏 南京 210094；2.南京工业大学城市建设与安全工程学院，江苏 南京 210009）

当高速射弹在可燃混合气中飞行时，由于射弹形状和速度、混合气性质、壁面（边界）条件的不同，将会形成多种形态的流场。例如，弹丸速度低于气体介质的CJ爆速时，不能形成爆轰波；而高于CJ爆速时，根据气体组分、压力、温度等，则可能形成驻定反应激波、驻定激波－爆轰复合波、附体驻定斜爆轰以及脱体爆轰波等多种流态，其中激波诱导燃烧和驻定斜爆轰波对于诸如冲压加速器、斜爆轰发动机等推进系统的研究有着重要意义。

C.I.Morris等［1］根据Rankine－Hugoniot关系式和有限反应速率模型，研究了尖劈作用下 H2／Air混合气中形成的斜激波或斜爆轰波，得到来流偏转角与激波倾斜角的极曲线图，并进行了实验验证。当尖劈角大于临界值时，爆轰波将脱体。该极曲线常用来分析尖劈或钝体诱导的驻定斜爆轰的特性。

飞行圆球和锥形圆柱诱导的爆轰比尖劈诱导的爆轰流场更复杂。J.Kasahara等［2］对超高速尖锥形圆柱在H2／O2预混气中的飞行进行了实验研究，并对气体初压大于和小于临界压力时爆轰波的结构进行了理论分析。结果表明，低于临界压力时，爆轰波阵面可分为3部分：过驱弓形爆轰波、强爆轰波和激波；高于临界压力时，爆轰波阵面分为4个部分：强过驱爆轰波、弱过驱爆轰波、准CJ爆轰波和CJ爆轰波。M.J.Kaneshige等［3］研究了圆球在两组不同组分的气体中的飞行，观察到激波诱导燃烧向驻定斜爆轰的转变过程。根据实验照片和数据，分析了影响驻定爆轰形成的相关参数，提出运用激波曲率来分析球形弹丸引发驻定爆轰条件。

P.Hung［4］基于单步不可逆反应，利用改进的ILDM方法对球形和尖劈形射弹引发的驻定斜爆波进行了二维计算，并运用衰变率模型进行分析，认为反应释放能量与激波弯曲熄火之间存在某种平衡，验证了M.J.Kaneshige等［3］提出射弹稳定爆轰的临界衰变率判剧。实验和计算结果都表明，可燃气体中，飞行的圆球弹丸诱发的爆轰波沿阵面逐渐衰减，从而形成由爆轰－反应激波－激波组成的复合波系。

本文中，从数值计算角度入手，采用带化学反应的Euler方程，以一定配比的H2／O2／N2预混气为研究对象，模拟计算飞行圆球在预混气中形成的爆轰波流场，并讨论这种超高速球形射弹引发的复合波系的流场特征，分析了波阵面结构和波后介质反应区变化。

1 物理模型和计算方法

二维轴对称的带基元化学反应的Euler方程为

式中：

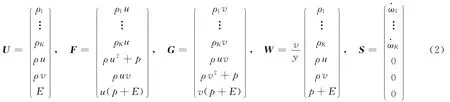
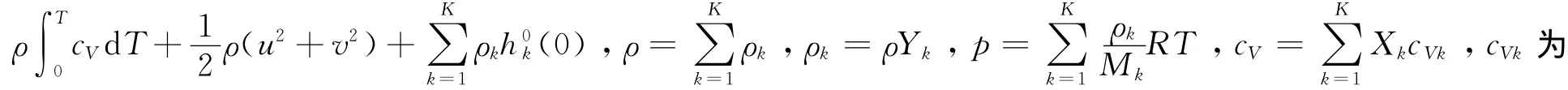
为组分k的净生成速率

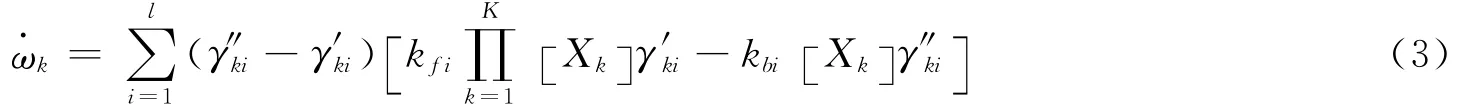
式中：γ′ki、γ″ki分别表示第i个基元反应中组分k的正、逆反应计量系数，Xk为组分k的摩尔浓度，kfi、kbi分别表示第i个基元反应的正、逆反应速率常数，他们遵循Arrhenius定律

式中：Afi表示第i个反应的指前因子，βfi表示第i个正反应的温度指数，Efi表示第i个正反应的活化能［5］。

反应流动系统中，流动特征时间和反应特征时间的差异常使方程带有刚性，为此，本文中采用分裂格式，将方程中的对流项和化学反应项分开处理。对流过程采用带Superbee限制器的、考虑横传波影响的波传播算法［6］，而化学反应过程则采用基于Gear算法的隐式方法。轴对称修正过程采用二阶Runge－Kutta法。计算时，对流项和轴对称修正项均采用量纲一量（量纲一的参考值为：压力p0＝101.325kPa，温度T0＝298.15K，长度L＝0.1m），而化学反应源项采用有量纲量［5］。

计算区域尺寸为5.0×3.0。弹丸位于轴线上，坐标为（2.0，0），直径为0.4，采用贴体网格，网格划分为250×150。下边界为轴对称边界，弹丸和上边界皆为固壁，采用滑移边界，左右两边界均为敞开的无梯度边界。

反应气体为初始压力为0.066、温度为1的φ（H2）∶φ（O2）∶φ（N2）＝2∶1∶7的预混气。采用19个基元反应和9种组分的化学反应机理。

2 结果分析

飞行圆球能否在可燃介质中形成爆轰，取决于流动特征时间与反应特征时间的差异，二者之比称为达姆科勒数Da＝tflow／tchem。对于飞行圆柱，流动特征时间tflow＝a／w（a是圆球半径，w是激波波后的气体法向速度），反应特征时间tchem＝ΔCJ／w（ΔCJ为反应区厚度），于是，Da＝a／ΔCJ。当反应特征时间大于流动特征时间时，即Da较小时，激波不能诱导燃烧；当反应特征时间减小，即Da较大时，激波可以诱导燃烧甚至形成爆轰。为了运用方便，常作如下简化：ΔCJ～，κ～1／a，其中P0为初始压力，κ为激波曲率，于是，Da＝P0／κ。即初压越高，激波弯曲程度越小，飞行圆球越易诱导燃烧。

实验时，通常是固定可燃组分、圆球尺寸、初温、飞行速度等，通过改变初压控制Da。实验表明［3］，存在一个临界初压，对应的达姆科勒数为Dcr。当Da＜Dcr时，不能诱导燃烧；Da＞Dcr时，可以诱导甚至形成稳定斜爆轰波。

讨论直径40mm的圆球，以U＝2 201.6m／s的飞行速度，在初始压力0.066、温度为1的φ（H2）∶φ（O2）∶φ（N2）＝2∶1∶7的预混气中的飞行，对应于Da略大于Dcr的情形。为考察所建立数理模型的有效性，参考 M.J.Kaneshige等［3］的高速弹丸诱导驻定爆轰的实验条件φ（H2）∶φ（O2）∶φ（N2）＝2∶1∶3.75，弹丸直径为25mm，速度为2.7km／s，p0＝42.1kPa）进行数值计算，图1（a）为文献［3］的实验结果，本文计算模型为二维模型，而实验照片为三维球体，考虑二者差异，调整计算参数获得图1（b）计算结果。从图1结果可看出，在适当条件下，圆球在可燃预混气中高速飞行，在圆球前端附近形成驻定爆轰波，下游远离圆球区域激波与燃烧波解耦，对比实验照片和计算结果，二者从波阵面和波后流场结构上都相似，表明可采用本文所建立的数理模型对圆球诱导驻定爆轰波流场进行定性分析。

图1 飞行圆球诱导流场的阴影图Fig.1Flow shadow photographs induced by a hypervelocity ball

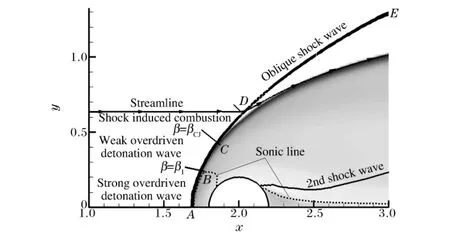
图2 驻定爆轰波结构Fig.2Standing detonation wave structure

图2为圆球附近局部区域燃烧产物的等位阴影图，图中实线为激波阵面，阴影的边缘代表燃烧阵面。根据预混可燃气初始状态及组分配比，经计算，爆轰波速DCJ＝1 703m／s，爆轰角为βCJ＝arcsin（DCJ／U）＝54°。

根据爆轰角变化、波后流体速度及介质反应状态，波阵面可分为如下4个区域。

（1）强过驱正爆轰（0≤β＜β1）

激波阵面上点A为爆轰阵面与中心轴线交点。该点附近，爆轰波阵面脱体，并与轴线垂直，沿爆轰阵面向下游移动，爆轰波阵面略有倾斜。波前来流速度大于CJ爆速，波后为亚音速。爆轰阵面的气流折转角几乎为零，但沿圆球壁面，气流方向改变很大，且由于壁面的强压缩效益而加速，向声速逼近。点B为声速点，此时，波后介质速度为当地声速，爆轰角为β1。

（2）弱过驱斜爆轰（β1≤β＜βCJ）

当β＞β1时，由于壁面压缩效应减弱，以及弹丸球形边界变化产生的膨胀稀疏波，使爆轰波减弱，爆轰阵面弯曲，倾斜角逐渐减小。波后的超音速气流在法向为亚音速，且逐渐升高。至点C波后气流法向速度为当地声速，该点称为CJ爆轰点，爆轰角为βCJ。

（3）反应激波

CJ爆轰点下游的阵面进一步弯曲，Da进一步减小，在稀疏波的作用下，激波强度降低，反应阵面与激波解耦，形成诱导燃烧的反应激波。通过阵面上点D的流线在引导激波后与反应区的边界重合。因此CD段激波诱导燃烧，但两者处于解耦状态，称为反应激波。

（4）惰性激波

过点D后，激波不足以引燃预混可燃气，因此DE段为惰性激波。

图3为圆球附近局部区域的马赫数等位阴影图，图中虚线为声迹线。在圆球的迎风面和背风面附近，各有一个声迹线围成的亚音速区，分别称为第1亚音速区和第2亚音速区。强过驱爆轰波后，气流为亚音速，在圆球前端壁面的压缩作用下，于第1亚音速区内加速，最终进入超音速区；波阵面上的其他区域，波后皆是超音速流动。超音速气流绕过圆球的子午线后，在扩散区域进一步加速。为了使球后中心轴上的气流趋于零，圆球下游出现第2道激波，从而使气流在波后减速，并在轴线上形成第2亚音速区。图4为压力等位阴影图，图中实线为流线。圆球前端第1亚音速区内的压力最高，然后，随流动区域的膨胀而逐渐降低，经第2激波压缩后，压力又升高。

图5为OH质量分数分布图。由图可见，在阵面AC区间，其波后滞止区存在大量OH自由基，说明此处的化学反应最激烈，火焰阵面与激波阵面耦合。随着激波的弯曲和衰减，OH质量分数逐渐减少，激波阵面与反应阵面也逐渐解耦，直至反应熄灭，此时激波不能诱导化学反应。

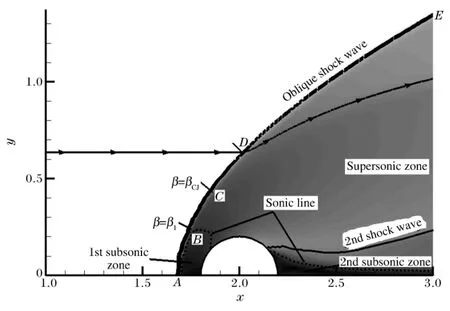
图3 Ma数分布及声速线Fig.3Distributions of Mach number and sonic line

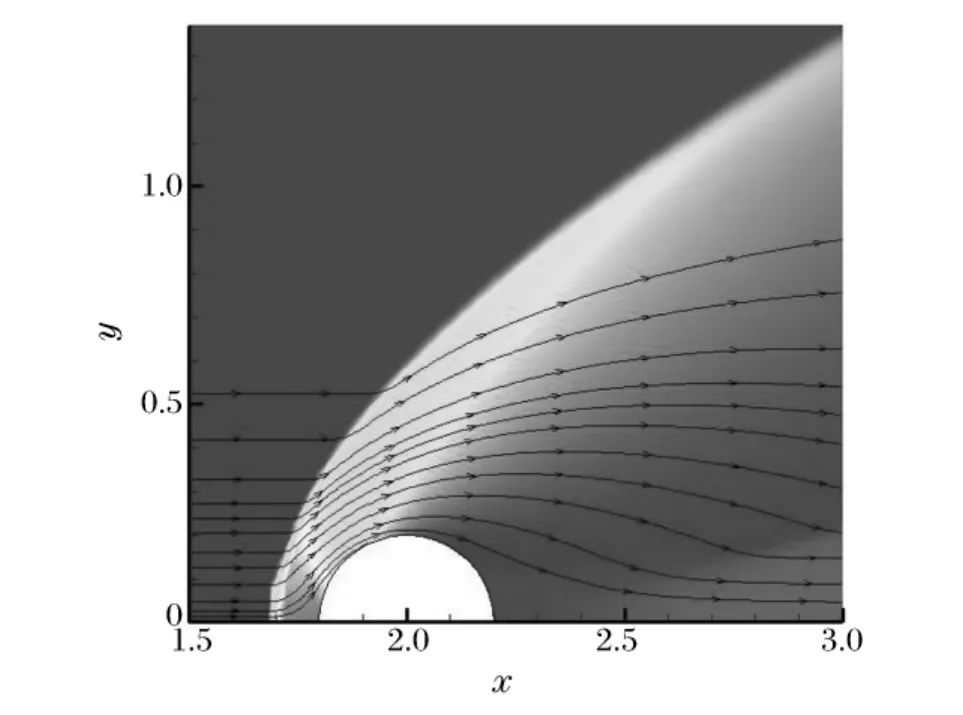
图4 压力阴影图及流线分布Fig.4Pressure shadow and streamline distribution

3 结 论

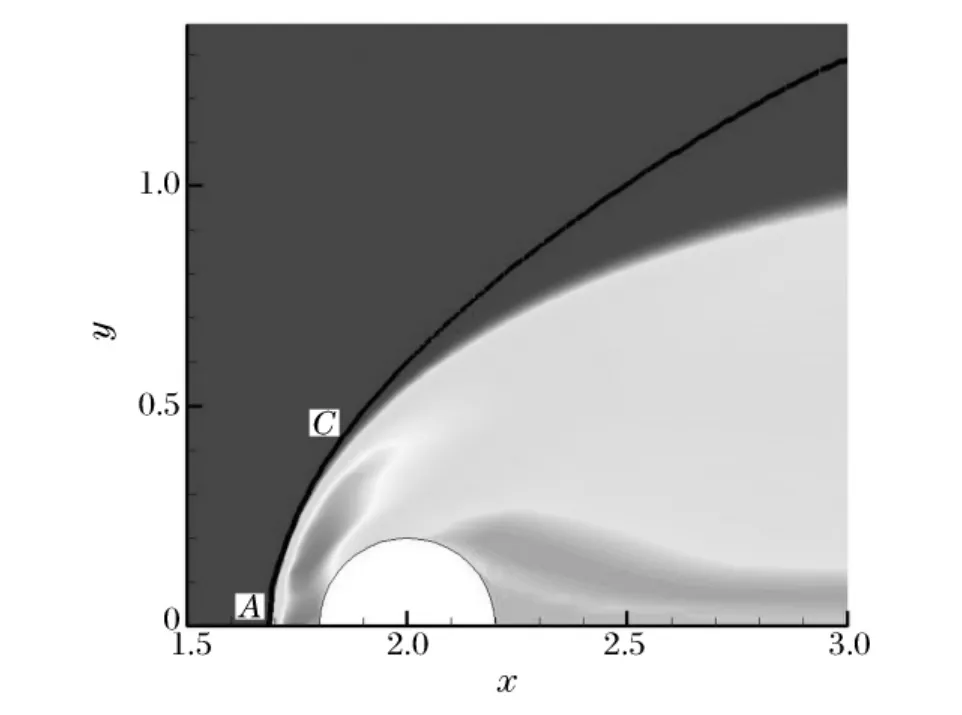
图5 OH质量分数分布Fig.5Distribution of the OH mass fraction

可燃介质中，超高音速飞行的圆球诱导的流场特性决定于达姆科勒数Da。参考实验条件，对Da略大于临界情形时圆球诱导的流场特征进行了数值研究。结果表明，在圆球诱导的驻定爆轰流场中，波阵面是一个由强过驱斜爆轰、弱过驱斜爆轰、反应激波和惰性激波组合而成的复合结构。由中心轴线至声速点波阵面为强过驱斜爆轰，波后流速为亚音速；由声速点至CJ爆轰点，圆球压缩作用减弱，波阵面为弱过驱斜爆轰波，波后流场为超音速；过CJ爆轰点激波强度减弱，燃烧波与激波开始解耦，形成分离的反应激波；沿波阵面过点D形成惰性激波阵面。流场中激烈反应区主要集中于第1亚音速区，于超音速区圆球背风面出现第2道激波，并于圆球下游轴线附近形成第2亚音速区。

［1］Morris C I，Kamel M R，Hanson R K.Shock－induced combustion in high－speed wedge flows［J］.Symposium （International）on Combustion，1998，27（2）：2157－2164.

［2］Kasahara J，Fujiwara T，Endo T，et al.Chapman－Jouguet oblique detonation structure around hypersonic projectiles［J］.AIAA Journal，2001，39（8）：1553－1561.

［3］Kaneshige M J，Shepherd J E.Oblique detonation stabilized on a hypervelocity projectile［J］.Symposium （International）on Combustion，1996，26（2）：3015－3022.

［4］Hung P.Algorithms for reaction mechanism reduction and numerical simulation of detonations initiated by projectiles［D］.Pasadena，California：California Institute of Technology，2003.

［5］归明月，范宝春，于陆军，等.聚心火焰与诱导激波相互作用及爆燃转爆轰过程［J］.推进技术，2007，28（3）：248－252.

GUI Ming－yue，FAN Bao－chun，YU Lu－jun，et al.Interaction of implosion flame and induced shock wave and DDT［J］.Journal of Propulsion Technology，2007，28（3）：248－252.

［6］Leveque R J.Wave propagation algorithms for multidimensional hyperbolic systems［J］.Journal of Computational Physics，1997，131（2）：327－353.