方形钢筋混凝土板的近场抗爆性能＊

汪 维，张 舵，卢芳云，汤福静，王松川

（国防科技大学理学院技术物理研究所，湖南 长沙 410073）

当爆炸在钢筋混凝土结构构件表面附近发生时，产生的冲击波会对结构构件造成损伤，因而准确预测潜在的爆炸对结构构件造成的损伤是进行重要建筑物和防护结构抗爆设计的基础［1］。由于爆炸载荷具有传播速度快、峰值大、作用时间短等特点，爆炸冲击载荷作用下钢筋混凝土构件和结构的动力响应很复杂。对钢筋混凝土板在爆炸载荷作用下的动力行为已开展了一系列的研究，如H.Y.Low等［2］分析了钢筋混凝土板在爆炸载荷作用下的剪切和弯曲失效；S.Chung Kim Yuen等［3］和G.S.Langdon等［4］通过实验和数值模拟研究了固支方板在爆炸载荷作用下的响应；XU Kai等［5］研究了钢筋混凝土板在爆炸载荷作用下的层裂破坏效应和抗爆性能；K.Ohkubo等［6］通过实验研究了纤维增强钢筋混凝土板的抗爆性能；阎石等［7］、张舵等［8］和汪维等［9］通过数值模拟研究了爆炸载荷作用下钢筋混凝土板的破坏模式和破坏效应。但由于问题的复杂性，对于单向方形钢筋混凝土板在近场爆炸载荷作用下的破坏模式和抗爆性能研究较少。

本文中拟首先进行单向支撑钢筋混凝土板抗爆实验，然后利用AUTODYN软件采用流固耦合算法，建立混凝土和钢筋三维分离式实体模型对实验过程进行数值模拟，且考虑应变率对钢筋和混凝土材料的动态本构特性的影响，并将模拟计算结果与实验结果进行比较，分析不同质量的装药作用下钢筋混凝土板的损伤机理和破坏特征，以期为工程应用和毁伤评估提供参考。

1 钢筋混凝土板爆炸实验

实验中用的钢筋混凝土板为自行配置浇注的方形钢筋混凝土板，边长为1 000mm，厚度为40mm，采用单层配筋，受力钢筋直径为6mm，间距为75mm；分布钢筋直径为6mm，间距为75mm。混凝土的单轴压缩强度测试值为39.6MPa，拉伸强度为8.2MPa，弹性模量为28.3MPa；钢筋的屈服应力为501MPa，弹性模量为200GPa。钢筋的布筋和支撑情况如图1所示。实验中，采用一种近似固支的方法将钢筋混凝土板固定，板端采用钢架固定，爆炸物悬挂在板的正上方400mm处，实验装置如图2所示。尽管实验的边界条件介于固定和扣牢之间，但固定的程度依赖于爆炸载荷的强度和边界所承受的损伤程度，这里钢筋混凝土板假设为固定支撑。

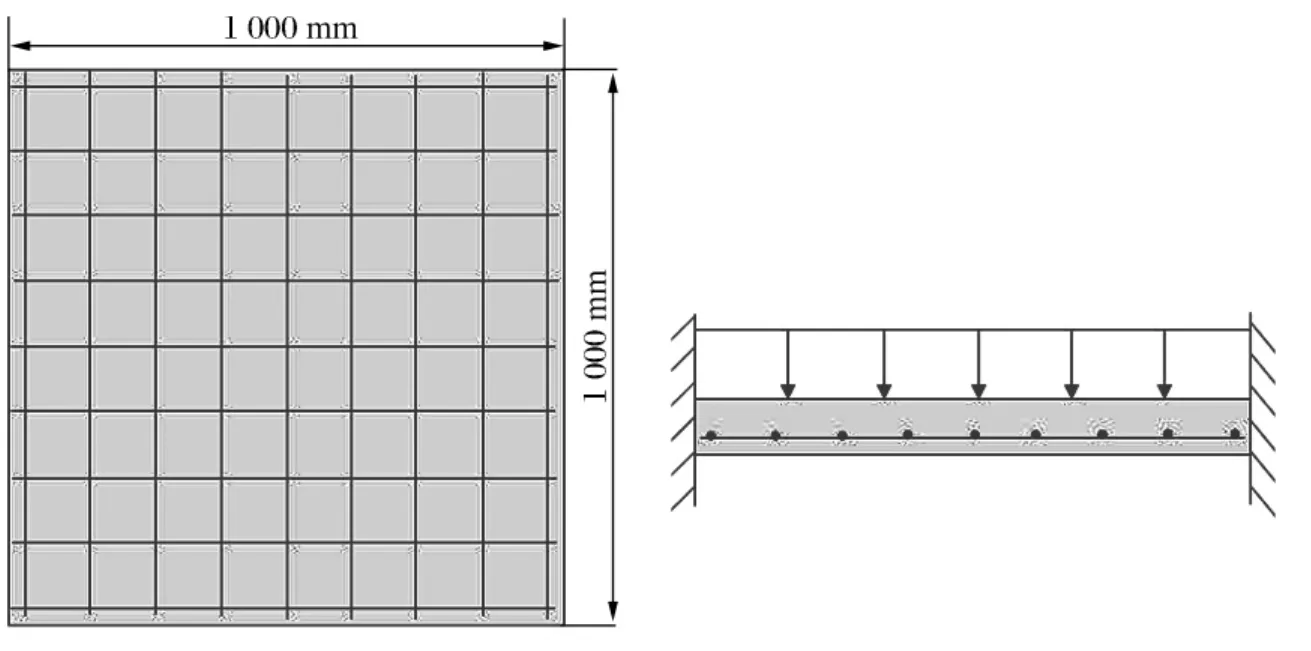
图1 钢筋混凝土板几何尺寸Fig.1Geometry of the reinforced concrete（RC）slab

图2 实验装置Fig.2Experimental device

为了获得不同的毁伤程度，采用2种不同质量的装药，实验结果和测量的参数如图3和表1所示，表中η为配筋率，m为装药质量，d为爆距，w为板中心挠度，r为层裂区半径。随着装药质量的增加，混凝土板中心挠度增加且底部层裂区域增大。在爆炸载荷作用下，压缩波在板的迎爆面产生损伤，并传播至板的背爆面形成强拉伸波，造成背爆面混凝土的剥落和层裂，实验中的破坏效果如图3所示，在板中心区域，出现多条环形裂缝和径向裂缝，具有双向弯曲的角部裂缝特征。钢筋混凝土板受拉区破坏严重，板背面中部出现多条横向受拉破坏的裂缝。随着装药质量的增加，正面和底面裂缝逐渐增加，钢筋混凝土板底部层裂区域面积逐渐增大，破坏程度增大。

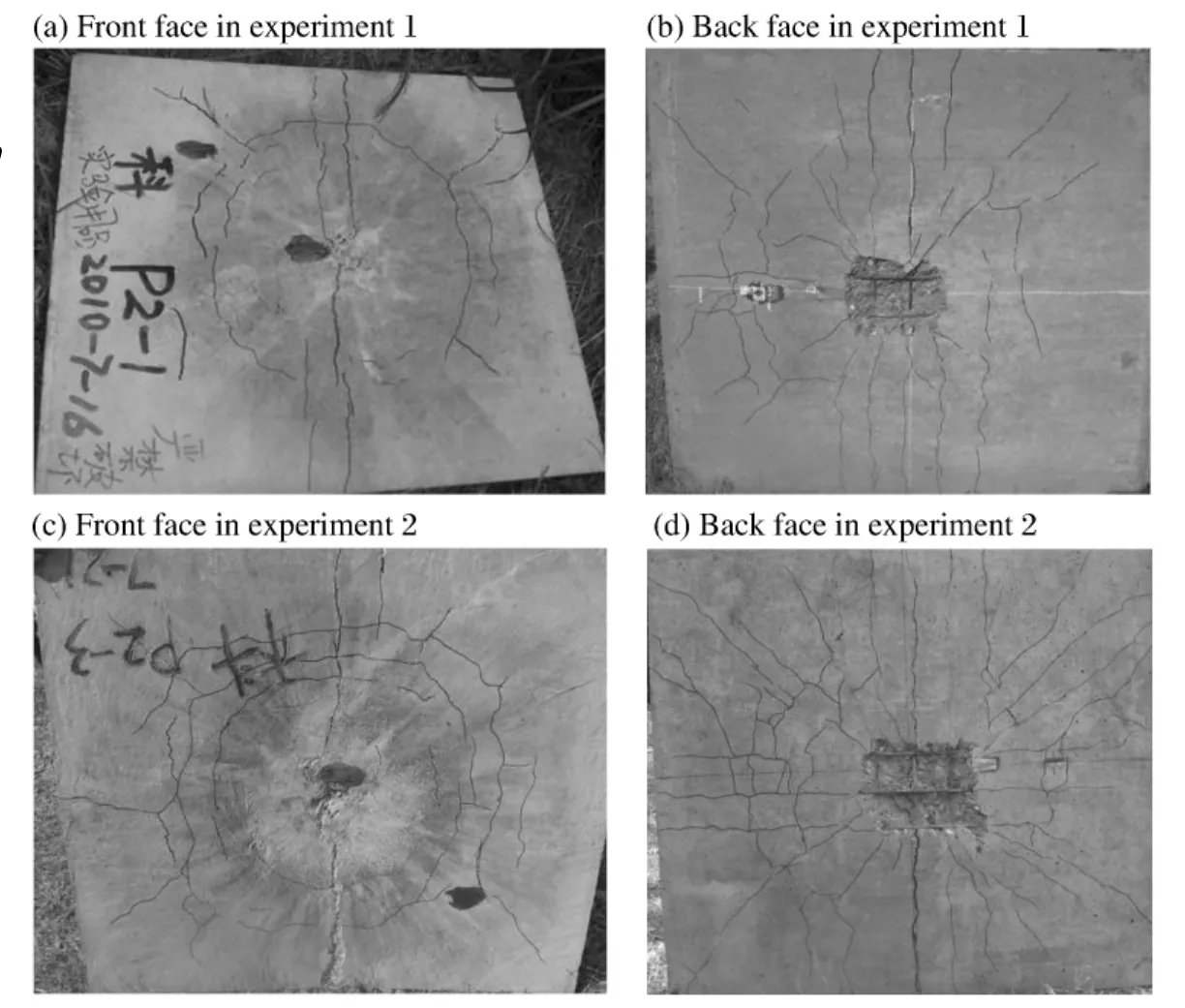
图3 实验中靶板的破坏效果Fig.3Experimental damage of the RC slabs in experiments

表1 空气中爆炸实验的测试参数Table 1Measured parameters for explosion experiments in air

2 计算模型和材料参数

2.1 计算模型和网格划分

在数值模拟中，为了减少计算量，首先使用一维网格对球面爆炸波到达目标壁面之前进行数值模拟，如图4所示。当冲击波波阵面到达距离爆心400mm处，即当冲击波接近钢筋混凝土板上表面，将冲击波映射到三维模型中计算它与钢筋混凝土板的相互作用，如图5所示。

由于结构具有对称性，对三维结构采用1／4模型进行计算；对钢筋和混凝土均采用Lagrange网格进行建模，网格大小为3mm，其中混凝土的单元数为386 825，钢筋的单元数为10 468，钢筋混凝土板的支撑条件为上下各加一层支撑盖板，计算时固定支撑盖板；对空气采用Euler－FCT算法，边界面设为物质流出；建立的钢筋和混凝土板有限元模型如图6～7所示。在爆炸载荷作用下，由于作用的时间很短，通常可以假定钢筋和混凝土之间的粘结是完好的，即建模时钢筋和混凝土接触单元共用节点，界面的分离条件为一旦混凝土或钢筋单元达到失效，则计算时将它删除，界面自动分离。同时混凝土单元的大变形会导致网格的扭曲，为解决网格的大变形问题，模型中采用侵蚀算法处理。这种算法将失效的混凝土单元自动删除，避免了网格扭曲造成的计算精度下降、计算步长变小等问题。

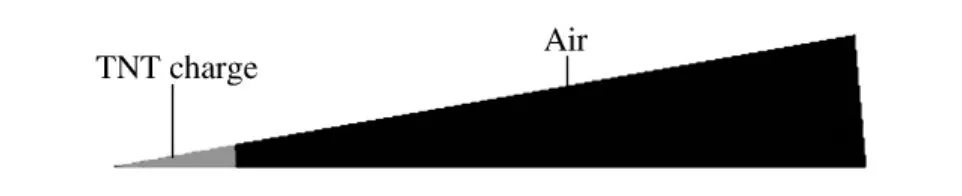
图4 TNT与空气的一维楔形模型Fig.4One－dimensional wedge model with axial symmetry for TNT charge and air

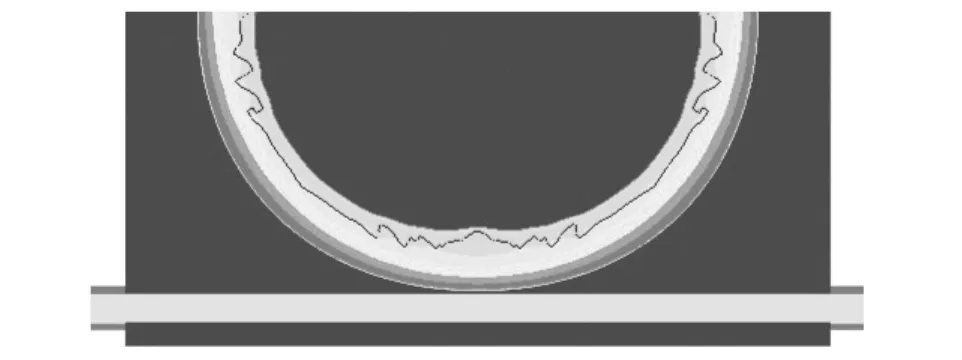
图5 冲击波传播的1／2模型Fig.5Shock wave pressure contours for half model

图6 钢筋布置Fig.6Rebar arrangement

图7 有限元数值模型的剖面图Fig.7Cross－section view of the numerical model

2.2 材料模型和状态方程

对TNT炸药的材料模型用JWL状态方程来描述

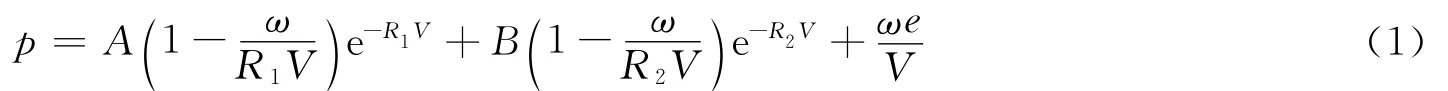
式中：p为爆轰压力，V为相对体积，e为比内能，A、B、R1、R2和ω为材料常数。TNT炸药的JWL状态方程参数［10］分别为：初始密度，1.610g／cm3；A，371.2GPa；B，32.3MPa；R1，4.15；R2，0.95；ω，0.3；初始比内能e0，7.0kJ／g；初始相对比体积V0，1.00。

对于空气，采用理想气体状态方程描述，具体材料参数［10］分别为：初始密度，1.293kg／m3；初始比内能，25μJ／m3；比热比γ，1.4。

钢筋和混凝土材料在爆炸载荷作用下，会经历高达10～1 000s－1的应变率［11］。在这种高应变率情况下，钢筋的强度能够提高50%，混凝土的抗压强度能够提高100%［11－12］，因此，本文中同时考虑了钢筋和混凝土的应变率效应。

对钢筋采用Johnson－Cook材料模型［13］，该模型适合描述材料在大应变、高应变率和高温下的力学性能。爆炸载荷作用下，热传导时间远大于爆轰持续时间，且由于变形热导致的温升不大，材料出现强化继而接近失效时，应力减小的幅度较小，所以温度软化效应不明显。该材料的本构模型可表示为

式中：εp为等效塑性应变，为等效塑性应变率为参考塑性应变率，A为材料的屈服强度，为对材料强化段的描述，C为应变率敏感因数。钢筋材料参数为：初始密度，7.83g／cm3；泊松比ν，0.28；A，300MPa；B，38.4TPa；n，0.26；C，0.014；，1s－1；失效应变，0.1。

对混凝土采用AUTODYN软件材料库中带损伤破坏的RHT混凝土材料模型，该模型包括p－α状态方程，RHT［14］强度模型和损伤模型以及侵蚀算法。RHT强度模型通过引进3个不同的强度面可以较好地表示混凝土材料所有的屈服强度、最大强度和残余强度的特性，能较合理地描述混凝土从弹性到失效的整个过程，较适合用来模拟混凝土材料在爆炸载荷作用下的动态响应。

混凝土在准静态载荷作用下的峰值拉应变为0.000 2（为峰值压应变的1／10），考虑到软化阶段，混凝土完全失效时的应变可认为是0.000 6。爆炸载荷作用下，混凝土的应变率为10～100s－1，相应的强度动力放大因子可达到5.0，甚至更大，但是断裂应变的增强比强度的放大小，因此混凝土的失效拉应变取为0.001。

失效面定义为压力p、Lode角θ和应变率的函数（见图8～9）

图8 最大强度、屈服强度和残余强度面Fig.8Maximum strength，yield strength and residual strength surfaces

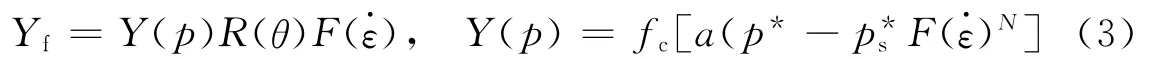
式中：fc是单轴压缩强度，a是失效面常数，N是失效面指数。p＊是用单轴压缩强度fc归一化的标准压力。是用单轴压缩强度fc归一化的标准层裂强度。定义R（θ）为应力第2不变量σeq、第3不变量det（S）和子午线比Q2的函数

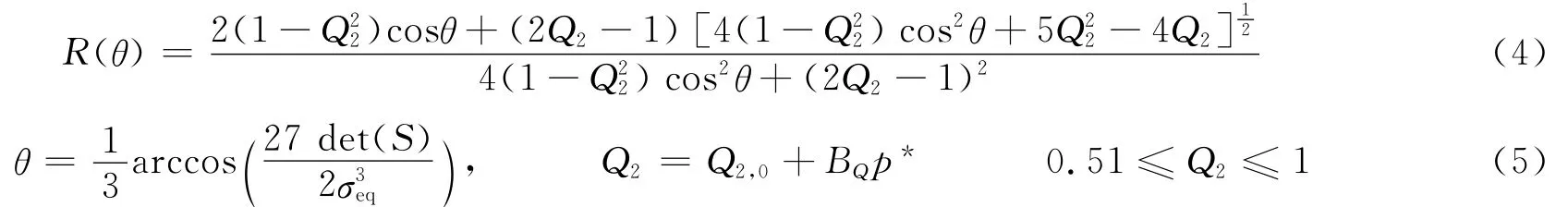
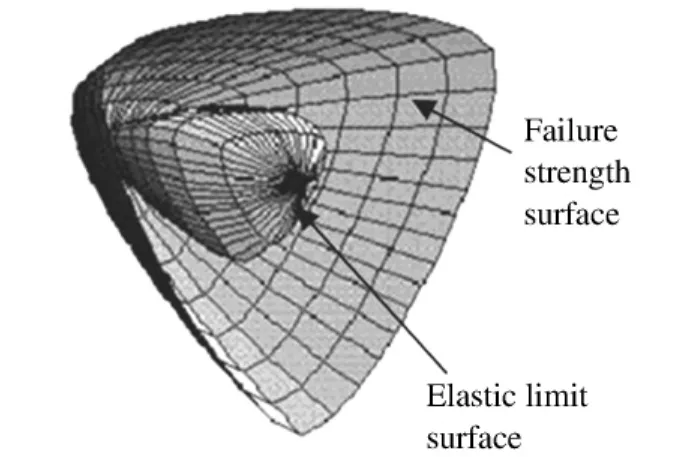
图9 三维屈服面Fig.9Three－dimensional yield surface

式中：BQ为过渡因子，Q2，0为材料的初始拉、压强度比ft／fc。弹性极限面Ye由失效面Yfai得到，定义为

式中：Fe是弹性强度与失效强度之比，Fcap（p）是弹性极限盖帽函数，用于限制静水压力p作用下的弹性偏应力。

残余强度面定义为

式中：b为残余强度面常数，M为残余失效面指数。

对混凝土软化段采用损伤软化，其中包括模量的软化和强度的弱化2部分，如图10所示，损伤度通过下式积累

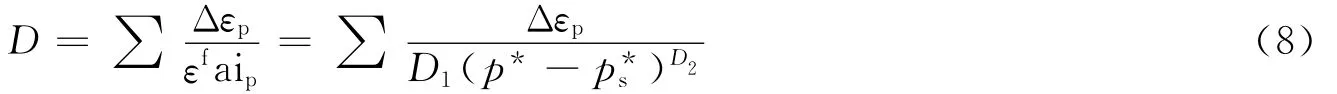
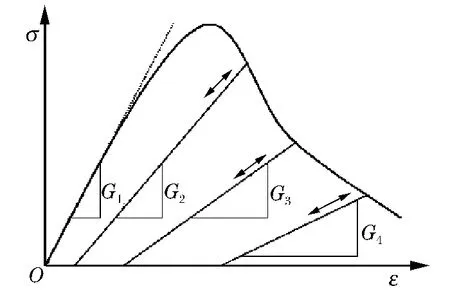
图10 损伤软化Fig.10Damage softness

式中：D1和D2为损伤常数；p＊s＝－T＊，T＊为拉伸极限压力。损伤失效强度和损伤剪切模量通过失效面和残余强度面插值得到。塑性应变的变化Δεp采用半径回归法求得。

强度的弱化和弹性模量的软化分别为

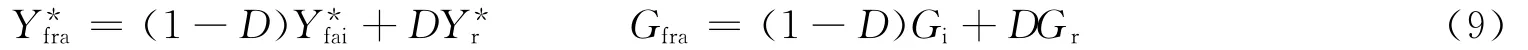
式中：Gi和Gr分别为无损剪切模量和残余剪切模量。

混凝土的 RHT材料模型参数为：初始密度，2.55g／cm3；Gi，280MPa；fc，40MPa；ft，4MPa；a，1.6；N，0.61；b，0.7；M，0.8；D1，0.04；D2，1；失效应变，0.001。其中混凝土抗压强度采用标准混凝土立方体试件进行抗压强度测试得到，其他参数均来自文献［10，15］。

3 计算结果与实验对比分析

3.1 数值模拟结果及分析

对实验1和2进行了数值模拟，数值模拟结果如图11所示。实验得到的板中心剩余挠度、层裂剥落区半径与计算结果的比较，如表2所示。从图11可以看出，计算结果与实验结果吻合较好，能够很好地展示钢筋混凝土板在爆炸载荷作用下的开裂、裂纹传播、底部层裂脱落过程。由于在爆炸实验过程中支撑混凝土板的支架可能产生一定的松动，后续对靶板的支撑可能不完全牢固，因而数值模拟得到的靶板支撑边界的破坏程度较实验中的破坏严重，因而板中心挠度较实验中的小；而由于混凝土的不均匀性，数值模拟得到的层裂和剥落区半径较实验得到的大。

图11 数值模拟得到的靶板破坏效果Fig.11Numerically simulated damage of RC slabs corresponding to experiments 1and 2

表2 数值模拟与实验结果的比较Table 2Comparison of results from simulations and tests

3.2 钢筋混凝土板动力响应与破坏模式分析

为了研究不同质量的装药对钢筋混凝土板毁伤破坏的影响，保持其他参数不变，对装药质量分别为0.20、0.31、0.46和1.00kg时钢筋混凝土板的破坏程度和破坏模式进行了分析。由于计算至钢筋混凝土板停止运动时间较长，本文中只计算t＝6ms时钢筋混凝土板的破坏程度。

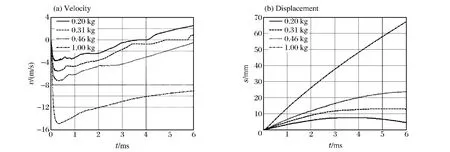
图12 不同质量的装药作用下钢筋混凝土板中心点的竖向速度和位移时程曲线Fig.12Vertical velocity－time and displacement－time curves of the middle points in the RC slabs under different blast loadings corresponding to different charge weights

由于爆炸作用下板跨中最大挠度是衡量其破坏程度的一个重要指标，板跨中最大挠度可以作为爆炸破坏程度的主要依据。对4种条件下板中心的位移时程曲线和速度时程曲线进行了对比，如图12所示。由图12可知，最大速度出现在爆炸冲击波结束（约0.25ms）时，而后钢筋混凝土板由于惯性作用将继续向下运动。另外，随着装药质量的增加，钢筋混凝土板跨中的挠度增大。当装药质量为0.20kg时，钢筋混凝土板在3.5ms时达到最大位移7mm，随后混凝土靶板开始回弹。当装药质量为0.31kg时，板的竖向位移为13mm。当装药质量为0.46kg时，板的竖向位移为24mm。1.00kg TNT装药作用下，钢筋混凝土板跨中在0.34ms达到最大速度14.93m／s，随后速度逐渐衰减，钢筋混凝土板发生了中部冲切破坏。4种质量的装药作用下钢筋混凝土板的破坏模式如图13所示，其中深色代表损伤度达到1，即材料已经失效；浅色代表损伤度为0，表示材料未损伤。

图13 不同质量的装药作用下钢筋混凝土板的损伤Fig.13Damage distribution of the RC slabs corresponding to different charge weights

图14 1kg TNT装药作用下钢筋混凝土板的损伤分布的侧视图Fig.14Side－viewed damage distribution of RC slabs in 1kg TNT charge case at different times

由图13可知，在不同的爆炸载荷作用下，压缩应力波均在板的迎爆面产生损伤，并传播至板的背爆面形成强拉伸波，造成背爆面混凝土的层裂和崩塌。随着装药质量的增大，钢筋混凝土板的破坏程度增大，并表现出不同的破坏模式。在0.20kg TNT装药作用时，板正面和背面有较少的纵向和环形小裂纹，靶板底部有部分小层裂区域，靶板中部纵向出现一条主要弯曲裂纹，板主要发生中部轻度弯曲破坏；当装药质量为0.31和0.46kg时，混凝土板受拉区破坏较严重，板背面纵向中部出现多条受拉破坏的裂缝，底部出现较大层裂区域，表现出明显的弯曲破坏。在1.00kg TNT装药作用时，钢筋混凝土板破坏严重，板整体表现为弯曲冲切破坏，中部横向裂缝增多，混凝土板被分割成许多块体，部分钢筋屈服但没发生断裂，在迎爆面与背爆面之间的板中心区域发生上下贯通破坏，形成了一个直径大于15cm的爆坑，破坏过程如图14所示。

4 结 论

采用AUTODYN软件建立了炸药、空气和钢筋混凝土板的三维数值模型，对方形钢筋混凝土板在单向支撑条件下的爆炸加载实验进行了数值模拟，并考虑了应变率对钢筋和混凝土材料动力本构特性的影响以及炸药、空气和结构之间的流固耦合相互作用，分析了不同质量的装药作用下钢筋混凝土板的损伤机理和破坏特征。结果表明：

（1）利用建立的流固耦合数值模拟方法可以合理地展现实验中钢筋混凝土板从混凝土开裂、底部层裂、部分钢筋屈服到板局部震塌的动态演变过程；

（2）在近爆载荷作用下，方形混凝土板中压缩应力波传播至板的背面形成强拉伸波，造成板背爆面混凝土的剥落和层裂破坏，层裂破坏区域随着装药质量的增加而增大；

（3）随着装药质量的增加，方形钢筋混凝土板的破坏逐渐由整体弯曲破坏转变为板中央局部的冲切破坏。

［1］LI Zhong－xian，DU Hao，BAO Chun－xiao.A review of current researches on blast load effects of building structures in China［J］.Transactions of Tianjin University，2006，12（zl）：35－41.

［2］Low H Y，Hao H.Reliability analysis of direct shear and flexural failure modes of RC slabs under explosive loading［J］.Engineering Structures，2002，24（2）：189－198.

［3］Chung Kim Yuen S，Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part I：Subjected to uniform blast load［J］.International Journal of Impact Engineering，2005，31（1）：55－83.

［4］Langdon G S，Chung Kim Yuen S，Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part II：Localised blast loading［J］.International Journal of Impact Engineering，2005，31（1）：85－111.

［5］XU Kai，LU Yong.Numerical simulation study of spallation in reinforced concrete plates subjected to blast loading［J］.Computers ＆ Structures，2005，84（5／6）：431－438.

［6］Ohkubo K，Beppu M，Ohno T，et al.Experimental study on the effectiveness of fiber sheet reinforcement on the explosive－resistant performance of concrete plates［J］.International Journal of Impact Engineering，2008，35（12）：1702－1708.

［7］阎石，张亮，王丹.钢筋混凝土板在爆炸荷载作用下的破坏模式分析［J］.沈阳建筑大学学报：自然科学版，2005，21（3）：177－180.

YAN Shi，ZHANG Liang，WANG Dan.Failure mode analysis for RC slab under explosive loads［J］.Journal of Shenyang Jianzhu University：Natural Science，2005，21（3）：177－180.

［8］张舵，卢芳云，王瑞峰.钢筋混凝土板在爆炸作用下的破坏研究［J］.弹道学报，2008，20（2）：13－16.

ZHANG Duo，LU Fang－yun，WANG Rui－feng.Study on destruction of reinforced concrete slab under blast loading［J］.Journal of Ballistics，2008，20（2）：13－16.

［9］汪维，张舵，卢芳云，等.钢筋混凝土楼板在爆炸荷载作用下的破坏模式和抗爆性能分析［J］.兵工学报，2010，31（增刊1）：102－106.

WANG Wei，ZHANG Duo，LU Fang－yun，et al.Analysis of blast resistance and damage model for reinforced concrete slab subjected to explosive loading［J］.Acta Armamentarii，2010，31（Suppl 1）：102－106.

［10］Century Dynamics Inc.Autodyn theory manual［M］.Concord，CA：Century Dynamics Inc，2006.

［11］Malvar L J，Ross C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1998，95（6）：735－739.

［12］Bischoff P H，Perry S H.Compressive behavior of concrete at high strain rate［J］.Materials and Structures，1991，24（6）：425－450.

［13］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the 7th International Symposium on Ballistics.Hague，1983：541－547.

［14］Riedel W，Thoma K，Hiermaier S，et al.Penetration of reinforced concrete by BETA－B－500numerical analysis using a new macroscopic concrete model for hydrocodes［C］∥Proceeding of the 9th International Symposium on Interaction of the Effects of Munitions with Structures.Berlin，1999：315－322.

［15］TU Zhen－guo，LU Yong.Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations［J］.International Journal of Impact Engineering，2009，36（1）：132－14.