基于通用炸药状态方程分析飞板运动规律的特征线法＊

李晓杰，赵春风，2

（1.大连理工大学运载工程与力学学部工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学工程抗震研究所，辽宁 大连 116024）

由于在滑移爆轰驱动下飞板的运动状态直接影响爆炸焊接工艺中各种参数的选择和焊接质量，所以研究飞板的运动规律是爆炸焊接理论研究中很重要的内容。对于稳定的滑移驱动飞板运动，将坐标系置于爆轰波头上，爆轰产物的流场就是定常的，可按二维可压缩定常流处理爆轰产物的流动，因此，可以采用特征线差分法对爆轰产物流场进行数值计算。以往在对这种定常爆轰流场进行计算时，一直用多方等熵方程来描述爆轰产物［1－5］，没有使用JWL和简化JWL等描述炸药爆轰的专用状态方程。这不仅影响爆轰流场的计算精确度，而且影响对爆轰驱动力学实质的分析。为此，本文中力求在使用通用状态方程的基础上，由二维可压缩定常流的基本理论导出特征线方程，并针对二维滑移爆轰飞板抛掷问题重新编制计算程序，以常用的JWL状态为例进行数值计算。沿用文献［1］中的爆轰波后采用的弱爆轰假设来处理声速面问题。另外，采用一种直接从物理概念出发获得等熵无旋定常超声速二维流动特征线方程的方法，而没有使用通常的由控制方程出发，采用不定线法或方向导数法来推导特征线方程的方法［6］，以期更明晰地描述特征线的物理意义。

1 二维定常超声速流的特征线方程

在均匀的超声速流场中，处于流场中某一固定点的小扰动源，所产生的扰动如图1所示，球对称地以声速c相对流体向外传播；流体本身以速度q运动，小扰动传播的绝对速度是声速c与流速q的矢量迭加。对于超声速流，有q＞c，扰动面是一个锥面，且与从扰动点出发的一串球面相切，该锥面为马赫锥，马赫锥的边界面（线）称为马赫面（线）。半锥角α为［1，5］

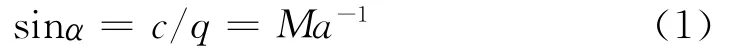
通常把半锥角α称为马赫角，Ma称为马赫数。

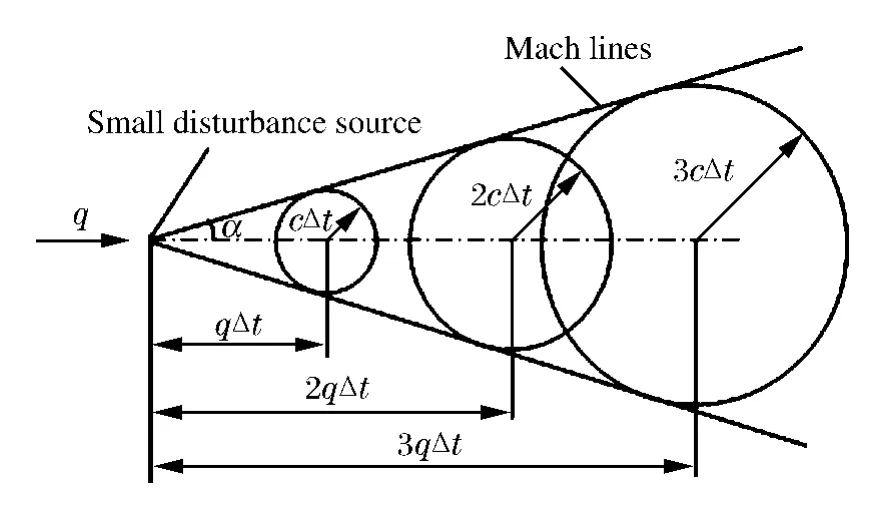
图1 超声速流中的小扰动Fig.1Aperturbation in supersonic flow

对于本文中要研究的平面问题，扰动源是无限长的线源，沿扰动线一系列马赫锥组成一个楔形。在二维平面上，如图2所示，马赫锥组成的楔形退化为2条马赫线I和II，在Oxy坐标系中，这2条马赫线的方程为［1，5］

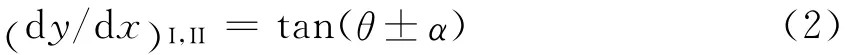
式中：θ是流动方向角。如果马赫波后的小扰动使流速由q变为q＋δq，流动方向角由θ变为θ＋δθ，则流动穿过马赫波I时，沿马赫波的平行方向的速度动量方程有

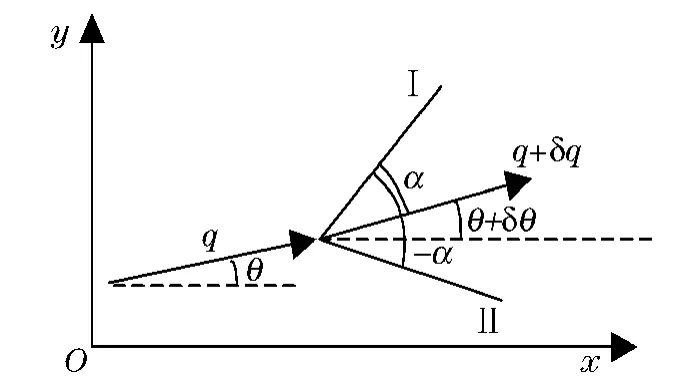
图2 超声速流中的特征线Fig.2Characteristic curves in supersonic flow

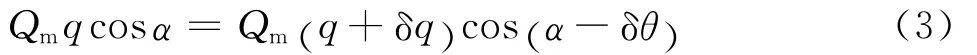
式中：Qm＝ρqsinα为通过马赫波上的质量流量。展开式（3），并考虑到δq→dq，δθ→dθ，且cosδθ→1，sinδθ→dθ，并忽略二阶小量，将式（1）代入式（3）可得

同理，对穿过马赫线II的参数变化可以写出

从数学意义上来讲，马赫线就是特征线，马赫线I和II分别对应第1族和第2族特征线，式（2）就是这2族特征线的方程，而式（4）和（5）分别是波阵面前、后的相容关系。任何复杂的超声速流场均可以被看成是由一系列连续的空间小扰动相互作用的结果，所以，常利用2族特征线方程和对应的相容关系来求解超声速流场。在进行数值求解时，一般使用沿特征线的相容关系。由于在超声速膨胀流中同族特征线不相交，一族特征线穿过另一族特征线，因此，一族特征线波阵面上的相容关系就是沿另一族特征线上的相容关系，所以可以获得沿第1、2族特征线上的相容关系为［1，5］

从物理概念出发获得的平面等熵定常超声速流动的特征线方程（2）和（6），由于方程式不依赖流体物态方程相关的参数，所以式（2）和（6）是通用物态方程的特征线关系。

然后，可以利用能量方程和具体的气体等熵方程来建立马赫数Ma和流速q与流动方向θ之间的关系。对于定常可压缩流，用热焓i和流速q的关系表示其伯努利方程［5，7］

式中：热焓i＝e＋p／ρ，e为比内能，p为爆压，ρ为炸药密度；i0为滞止焓。微分式（7）可得

再利用Ma2＝ （q／c）2＝2 （i0－i）／c2，等熵条件di＝dp／ρ和声速c2＝（∂p／ ∂ρ）S＝dp／dρ，由上面推导可以得到下面的关系

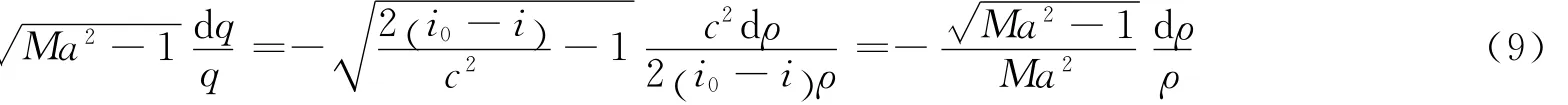
由于在等熵线上，流体的热焓i、声速c，包括马赫数Ma都是密度ρ的单值函数，所以式（9）是可以积分的，故可以将式（9）的积分定义成一个函数

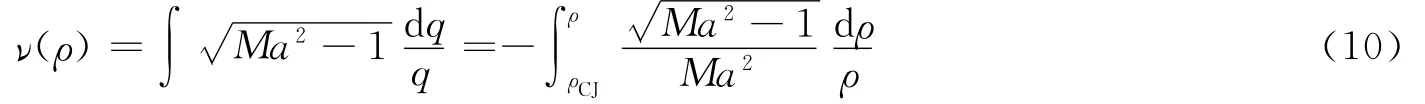
式中：函数ν（ρ）相当于Prandtl－Meyer（P－M）函数［6］，ρCJ为炸药CJ状态时的密度。

将式（10）定义为不依赖流体状态方程的P－M函数，或称为通用状态方程的P－M函数。在式（6）中引入该函数写成新的特征线相容关系，再与式（2）合并，可以写成如下超声速定常流特征线方程组

式中：RⅠ和RⅡ是常数，分别为第1和第2黎曼不变量。显然，只要根据具体的流体等熵状态方程求出热焓i、声速c代入式（10）求得P－M函数ν（ρ），就可以和式（11）组成封闭的求解方程组了。如对于常用的JWL炸药状态方程，其等熵方程如下

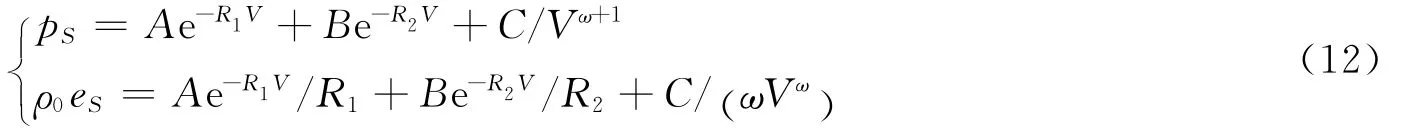
式中：pS为等熵压力，eS为等熵比内能，ρ0为初始密度，A、B、C、R1、R2和ω为常数，V＝ρ0／ρ是相对比体积。根据相应的定义可以推导出JWL状态方程的声速和热焓表达式

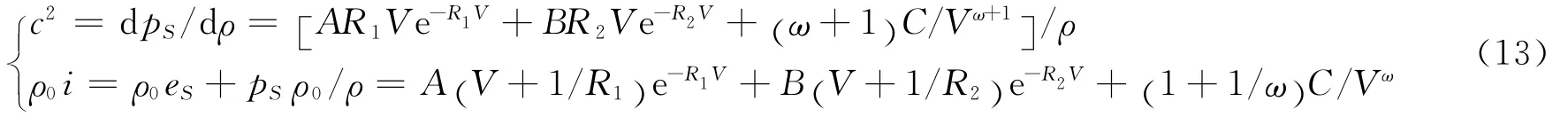
由于特征线方程（11）为常微分方程组，所包含的P－M函数ν（ρ）可以用辛普森积分等高精度积分方法求解，所以使用特征线方程可以获得高精度的差分解。

2 滑移爆轰驱动飞板的特征线差分法

在确立了平面超声速流的特征线方程后，可将特征线方程离散化，对图3所示的滑移爆轰驱动飞板问题进行数值计算。

2.1 初值选取

如图3所示，炸药向空气飞散在O点处可以近似用中心稀疏波处理。由于在爆轰波CJ面上的马赫数MaCJ＝1，对应的密度ρ＝ρCJ，气流转角θ＝0，根据普朗特绕流理论的第2族特征线相容关系式［7］

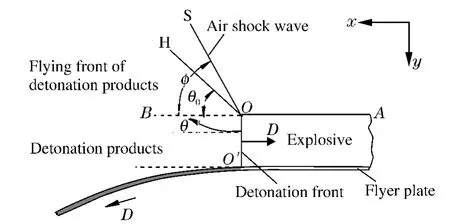
图3 滑移爆轰作用下的飞板运动姿态Fig.3Movement of flyer plate driven by glancing detonation

可以在ρCJ到某一较小ρn范围内给出一系列的离散点（ρi，θi），其中i＝0，1，2，…，n；离散点的（x，y）坐标均在O点处，这些离散点就是差分的初值点。再利用下式确定滞止焓

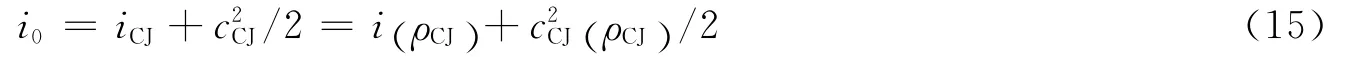
2.2 声速面处理

由于在爆轰产物流场中，爆轰波面后的CJ面是声速面，从O点发出的马赫线会在飞板壁面上垂直反射，导致无法计算差分值。具体的处理方法可以简单地令炸药爆轰稍向弱爆轰方向偏离CJ点［5］，只对整个流场产生微小的影响。即令＝ （1－Δ）ρCJ，使爆轰波后完全变为超声速流场，就完全可使用特征线差分求解。这样做引起的误差也很小，把Δ取足够小量，对计算结果影响不大。在实际计算中，Δ可取为10－2～10－3量级，对量纲一压力的扰动为10－4～10－6量级。

2.3 超声速流场域内差分

在爆轰产物的超声速流场内部，如图4所示，当已知点1、2的流动参数时，可以用2族特征线相交求取出未知点3上的参数。由式（11）将第1族特征线RⅠ方程由已知点1至未知点3离散成差分形式，第2族特征线RⅡ方程由已知点2至未知点3离散，经联立整理可得

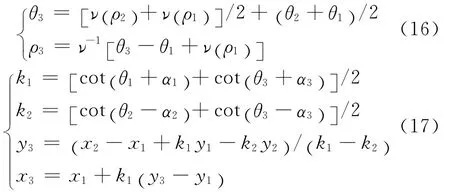
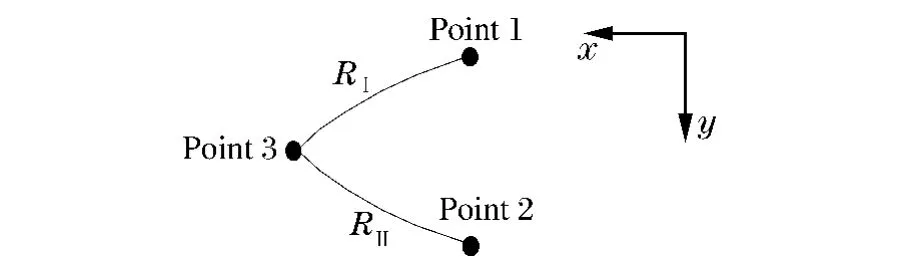
图4 爆轰产物中差分示意图Fig.4Scheme of differences in detonation products

式中：下标1～3分别表示点1～3。按式（16）由点1、2的参数差分解出θ3，进而用P－M反函数求得ρ3。然后，利用状态方程，求解最后代入式（17）确定点3的坐标。

2.4 飞板边界差分

飞板在爆轰压力驱动下的运动微分方程为［6］

式中：R为炸药质量比，即炸药的厚度和密度的乘积与飞板的厚度和密度乘积的比值；＝p／pCJ，pCJ为等熵状态的爆轰压力；D为炸药爆速；pk为中间变量；x、y为药厚量纲一化的坐标。如图5所示，当已知飞板边界点1和流场域内点2时，可利用飞板运动方程（18），与通过点2的第1族特征线求出点3的参数。将上述边界方程作如下离散

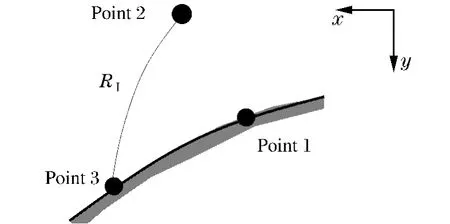
图5 飞板边界差分示意图Fig.5Scheme of differences on the boundary of flyer plate

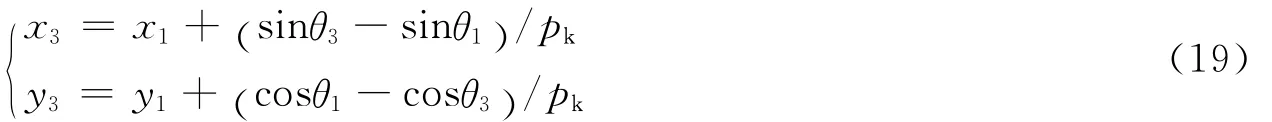
对通过点2、3的第1族特征线方程也离散成差分形式

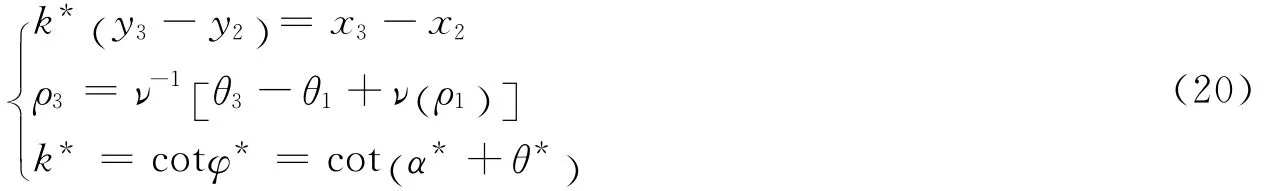
将式（19）代入式（20），整理得

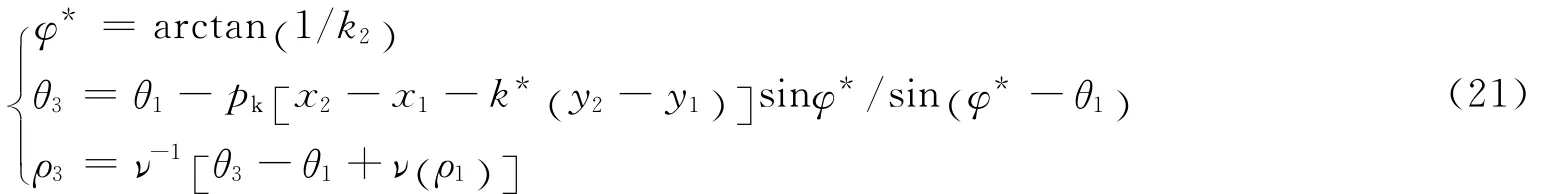
预估方程组（21）可以用预估－校正法获得较高的差分精度。具体做法是，以k＊＝cot（θ2＋α2）和pk＝Rp1／（ρ0D2）作为预估初值代入式（21）解出θ3、ρ3，并用状态方程解出对应的点3的i3、c3、Ma3和α3；再用k＊＝ ［cot（θ2＋α2）＋cot（θ3＋α3）］／2和pk＝R（p1＋p3）／（2ρ0D2）代入式（21），重新求解一遍，可获得经过校正的点3的参数。最后，用式（19）求出点3的坐标。

2.5 实例计算

用上述通用状态方程的差分格式和方法，编制计算程序对飞板二维抛掷问题进行数值求解。计算中TNT炸药的JWL状态方程参数［8］：多方指数K，2.727 6；CJ状态的密度，1.630g／cm3；CJ状态的爆压，21.0GPa；CJ状态的爆速，6.93km／s；A，373.8GPa；B，2.747GPa；C，0.734GPa；R1，4.15；R2，0.90；ω，0.35。乳化炸药的JWL状态方程参数［9］：多方指数K，3.008；CJ状态的密度，1.145g／cm3；CJ状态的爆压，7.62GPa；CJ状态的爆速，5.141 4km／s；A，326.42GPa；B，5.808 9GPa；C，1.032 5GPa；R1，5.8；R2，1.56；ω，0.57。图6为所计算的 TNT和乳化炸药滑移爆轰驱动飞板的抛掷曲线，图7为飞板的动态弯折角与量纲一飞行距离的关系，图8为TNT、乳化炸药的JWL和多方方程的等熵卸载线。

由图6～7可以看出，对于TNT炸药，用多方状态方程描述的对飞板的加速能力较用JWL方程描述的大；取量纲一距离飞行距离y＝1处的弯折角进行对比，分别为11.96°和10.57°，用JWL状态方程的计算结果较用多方方程的计算结果小11.62%。对于乳化炸药，用多方状态方程描述的对飞板的加速能力较用JWL方程描述的小；取量纲一距离飞行距离y＝1处的弯折角对比，分别为11.20°和12.31°，用JWL状态方程的计算结果较用多方方程的计算结果大9.91%。这与图8等熵膨胀线所表示的炸药膨胀做功能力完全一致，即TNT的JWL等熵膨胀线在多方方程等熵线的下方，膨胀做功能力较小；乳化炸药的JWL等熵线居于多方方程等熵线的上方，做功驱动能力较大。由此可见，通用状态方程特征线差分方法能够正确地反映飞板的爆轰驱动过程。

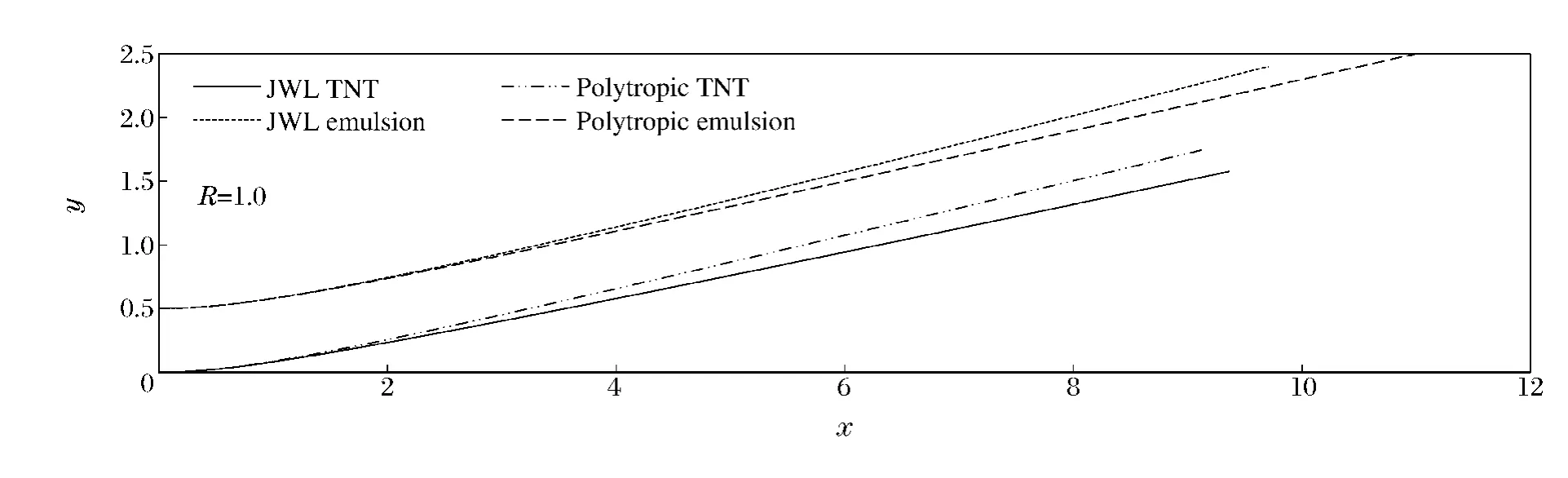
图6 爆轰驱动飞板的抛掷曲线Fig.6Flying curves of flyer plate driven by detonation

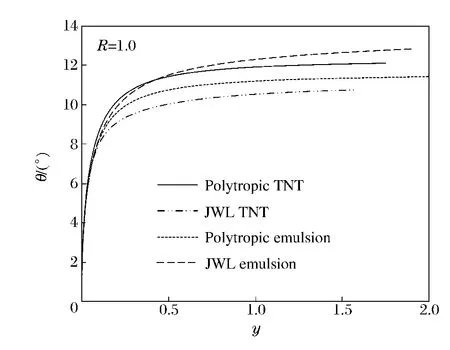
图7 飞板量纲一飞行距离与弯折角的关系Fig.7Relationship of dimensionless flying distance and bending angle for flyer plate

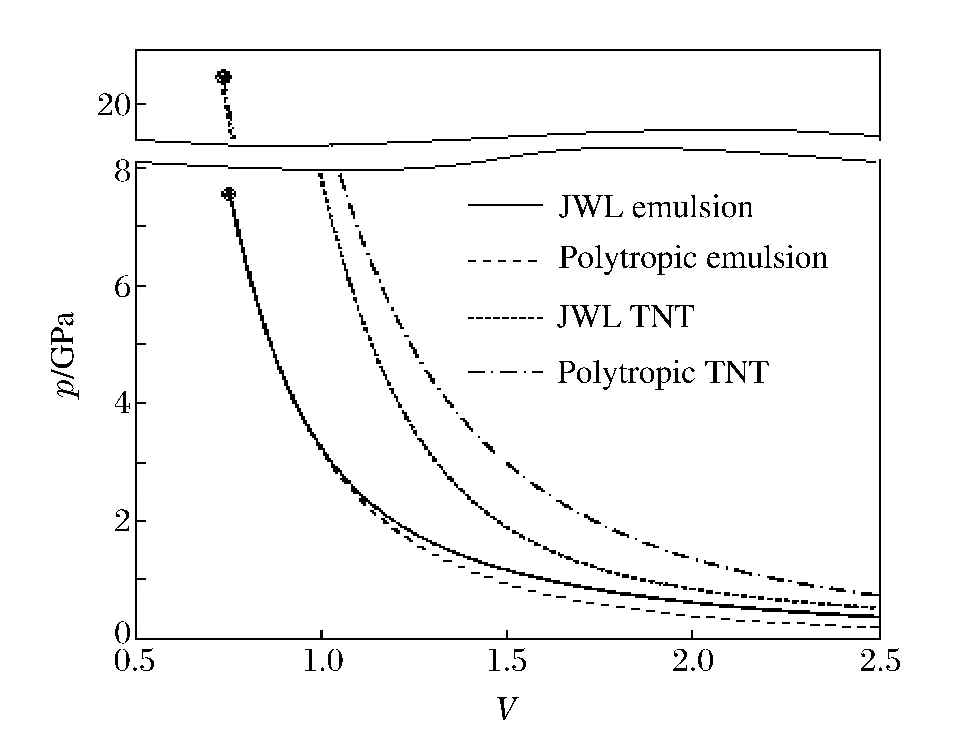
图8 JWL等熵线与多方等熵线的对比Fig.8Comparision of JWL and polytropic isentropic curves

3 结 论

（1）从马赫波的物理概念出发，推导出了平面二维超声速定常流的特征线方程；并且重新定义了以流体密度为单一自变量的Prantl－Meyer函数ν（ρ），从而构成了求解平面二维超声速定常流的封闭方程组。由于所获得的特征线微分方程组不依赖流体状态方程的表达形式，所以可以用于流体各种形式状态方程的求解，是一种通用物态方程的超声速定常流特征线求解方法。

（2）为了检验通用物态方程特征线解法，针对滑移爆轰驱动飞板运动问题构建了爆轰产物流场内部和飞板边界特征线差分法格式，对爆轰波头声速面的处理采用了向超声速的弱爆轰摄动的处理方法。

（3）对TNT炸药和乳化炸药采用JWL状态方程与多方方程进行对比计算的结果表明，这种通用状态方程特征线差分方法可以准确地反映炸药状态方程对飞板抛掷的作用，飞板的爆轰驱动过程与其状态方程所表述的做功驱动能力一致。

最后应该说明的是，特征线差分方法所求解的方程组本质上是常微分方程组，所以完全可以参照常微分方程组的数值求解方法（如欧拉预估－校正法）获得高精度特征线差分格式，从而提高定常爆轰驱动问题的求解精度。另外，由于特征线差分方法计算简单，并且可以很好地反映滑移爆轰驱动问题的实质，如果将通用状态方程特征线差分程序作为参数优化程序的内嵌，可以构成精确简单的炸药状态方程参数拟合程序，简化炸药状态方程的参数拟合计算过程。

［1］李晓杰.滑移爆轰下带覆盖物的飞板抛掷及对切割的影响［D］.大连：大连理工大学，1987.

［2］Besshaposhnikov Y P.Motion of a plate thrown by aglancing detonation wave［J］.Combustion，Explosion，and Shock Waves，1999，35（1）：109－112.

［3］Ivanov A G，Kochkin L I，Ogorodnikov V A，et al.Characteristics of the acceleration of plates by aglancing detonation wave in the presence of an additional or concentrated mass［J］.Combustion，Explosion，and Shock Waves，1990，26（5）：612－614.

［4］邵丙璜，张凯.爆炸焊接原理及其工程应用［M］.大连：大连工学院出版社，1987.

［5］吕洪生，曾新吾.连续介质力学（中册）：流体力学与爆炸力学［M］.长沙：国防科技大学出版社，1999.

［6］Courant R，Friedrichs K O.Supersonic flow and shock waves［M］.5th Edition.New York：Springer－Verlag，1976：37－75.

［7］赵春风.基于通用状态方程的爆炸焊接特征线法研究［D］.大连：大连理工大学，2010.

［8］徐锡申，张万箱.实用物态方程理论导引［M］.北京：科学出版社，1986：402－403.

［9］宋锦泉.乳化炸药爆轰特性研究［D］.北京：北京科技大学，2000.