基于匹配追踪算法的复合材料冲击损伤成像技术*
2012-06-20冯勇明
冯勇明,周 丽
(南京航空航天大学机械结构力学及控制国家重点实验室,江苏 南京 210016)
先进的复合材料已在航空航天飞行器结构上得到了广泛应用,但复合材料结构在制造和使用过程中,不可避免地会受到损伤,尤其是低能量物体的冲击造成的损伤,这种损伤往往表现为目不可检的内部分层、基体开裂和纤维断裂,对结构的安全使用造成严重威胁。因此,及时准确检测并识别出复合材料结构内部损伤、确定损伤程度并进行连续监测是当前关注的焦点。目前,在复合材料结构的健康监测领域,Lamb波能在结构中传播较长的距离,被认为是较有前景的一种局部损伤检测方法[1-2],非常适合监测机翼和机身这样的大面积结构[3-4]。在结构中布置一定的传感器,主动激励Lamb波信号,通过对接收的损伤前和损伤后的Lamb波信号进行一定的处理,就可以提取应力波包含的与损伤有关的特征信息,从而进行损伤定位及损伤大小的判断[5]。
T.R.Hay等[6]对蜂窝夹层结构中应力波的传播特性进行了研究,为基于应力波的损伤监测方法在复合材料结构中的应用提供了指导。M.M.Howard等[7]验证了压电传感器环方法监测复合材料结构的可行性;A.Swartz等[8]分别采用小波衰减法、功率谱的相关系数法等监测方法对结构中的损伤进行了监测。近年来,许多学者[9-11]采用短时傅里叶变换(STFT)、小波变换(WT)、希尔伯特-黄变换(HHT)等时频分析方法对监测信号进行分析,并取得了一系列成果,但这些方法的时频分辨率都不理想,并且未考虑弥散效应对信号的影响。J.C.Hong等[12]将匹配追踪方法运用于应力波信号的处理中,但他们假设应力波信号是单模态的、非弥散的,并未精确建立弥散效应与原子的调频斜率之间的关系,计算结果精度不高。
本文中,使用Chirplet原子匹配弥散的窄带脉冲信号,并采用自适应信号处理方法——匹配追踪方法对监测信号进行分解,对Lamb波信号进行时频分析,证明Chirplet原子能准确匹配失真变形的窄带脉冲信号。利用对碳纤维复合材料板的冲击损伤进行实验检测,采用匹配追踪方法对包含有损伤信息的应力波信号进行时频处理,提取损伤特征值,并采用损伤概率成像方法定位结构中的冲击损伤。
1 匹配追踪方法
匹配追踪(matching pursuits,MP)方法是S.G.Mallat等[13]在1993年提出的一种自适应信号处理方法,该方法将待分析信号重复迭代投影到庞大的波形字典库中,并从字典库中选择最适合匹配某段待分析信号的波形。MP方法克服了STFT变换中窗函数固定,以及小波变换中窗函数的频率参数与尺度参数成反比的缺点,使用能匹配信号时频特性的波形来灵活地表示信号。MP方法的核心问题是构建庞大的冗余字典库,并从中快速检索出最佳的匹配原子,字典库检索的计算速度问题显得尤为重要。
设D={gr}r∈Γ是由P>N个范数为1的向量所形成的字典库。该字典库中包含N个线性无关的向量,这N个向量构成长度为N的信号空间CN的一组基。匹配追踪算法首先将信号f投影到一个向量gr0∈D上,并计算出余项Rf,

由于Rf与gr0正交,因此

为了极小化 ‖Rf‖,取gr0∈D,使得 〈f,gr0〉为极大值。在某些情况下为使计算更为有效,只需找到向量gr0使之几乎为最优

式中:α∈(0,]1为最佳因子。匹配追踪方法通过反复地迭代对余项作进一步分解。记R0f=f,对m≥0,设第m个余项Rmf已经计算出来,那么下一步迭代是选取gr0∈D,使得

将Rmf投影到grm上,得到

由Rm+1f与grm的正交性,得到

即整个分解过程是满足能量守恒定律的。对m从0到M-1求和,得

当m→∞时,‖Rmf‖按指数级收敛于0。迭代过程可以通过指定迭代次数或控制信号残值完成。
根据实际应用可以选择特殊的字典D。在结构健康监测中,主要应用时频原子字典,如Gabor原子、Chirplet原子等。在进行具体的标准匹配追踪算法时,连续的参数空间必须适当地离散化。本文中,匹配追踪方法选用由Chirplet原子组成的字典库
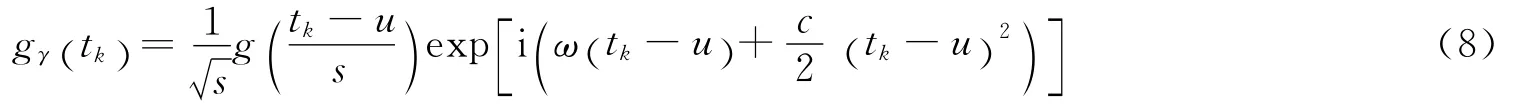
式中:tk表示时间离散点,g(tk)=;索引γ=(s,u,ω,c),其中s为尺度,u为时间中心,ω0为角频率中心,c为调频斜率。该原子的角频率ω(tk) 随时间变化,ω(tk)=ω+c(tk-u)。Chirplet原子以及WVD分布如图1所示。
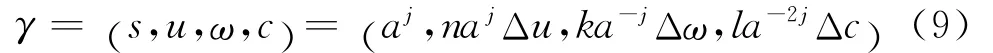
式中:j、n、k、l为整数。
研究中模拟与实验测得信号均为实数信号,应用MP算法时需要使用实数原子
Chirplet原子组成的字典库是Gabor原子组成字典库的延伸,当Chirplet原子中的变量c=0时,Chirplet原子即为Gabor原子。Chirplet原子字典库的索引离散化后为
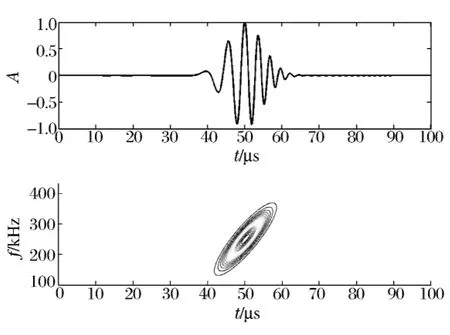
图1 Chirplet原子及其WVD分布Fig.1The Chirplet atom and its WVD
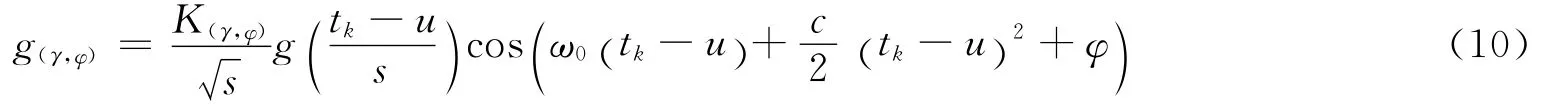
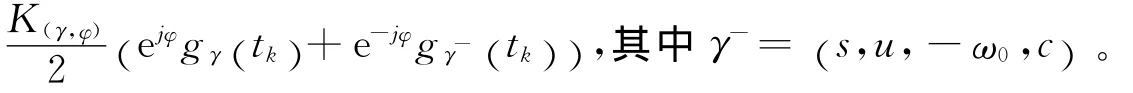
2 数值模拟验证
为验证本文中提出的MP方法的有效性,建立带损伤铝板的二维有限元模型。模型如图2所示,尺寸为80cm×0.1cm,在距离压电片12和21.5cm处布置缺口用来模拟损伤,缺口尺寸为0.025cm×0.05cm。在模拟时采用2对剪切力模拟激励源产生应力波。激励信号采用窄带波信号

式中:尺度s为量纲一因数,s=6×10-6,激励频率f0=250kHz。
MP方法对模拟结果进行分解重构后的信号如图3(a)中虚线所示,重构信号与模拟几乎重合,表明Chirplet原子能很好地匹配弥散脉冲。MP方法得到的时频能量分布如图3(b)所示,能得到信号的时频能量分布图,并能分辨中间2个重叠的反射信号。图3(c)是信号的小波尺度谱,它不能分辨重叠在一起的反射信号。
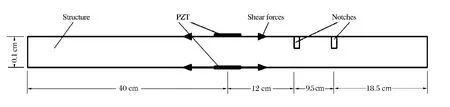
图2 数值模拟模型Fig.2The model of numerical simulation
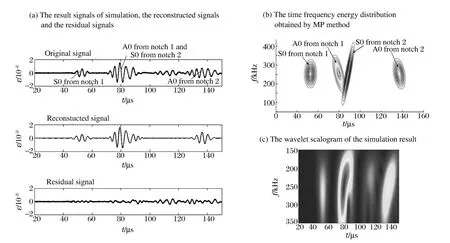
图3 模拟结果分析Fig.3The results of numerical simulation
3 损伤概率成像方法
3.1 基于信号能量谱的损伤指标
在结构运行之前的完好状态下测得Lamb波信号,称为基准信号;然后在结构运行之后,再次测得Lamb波在结构中的传播信号,称为监测信号;将监测信号与基准信号进行比较以判断结构中是否存在损伤,并进一步确定损伤的位置、程度等信息。监测信号与基准信号之间的差异系数,称为损伤指标(DI),本文中通过提取结构损伤前后Lamb波信号能量特征的差异系数即DI来确定损伤指标。选用Chirplet原子对基准信号和监测信号分别进行MP变换,提取信号主要频带的局部时间-能量密度,定义损伤指标如下
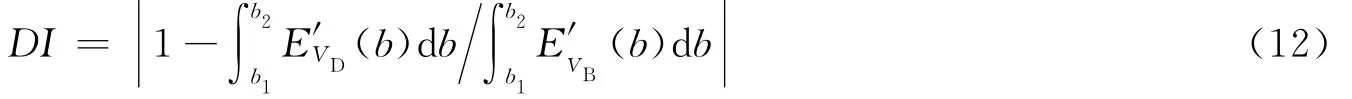
式中:VB是结构完好状态下测得的Lamb波基准信号,VD是结构损伤后测得的Lamb波监测信号,E′(b)是信号经过 MP分析后在尺度 [a1,a2]、时刻b下的局部时间 -能量密度,[b1,b2]表示对信号进行MP分析的时间范围。
理想情况下,如果结构中不存在损伤,那么VB和VD完全相同,DI=0。但在实际情况中,由于外界环境如温度、湿度、噪声等影响,即使在无损状态下测得的监测信号也会与基准信号有不小的差别,难以区分这一差异是由结构损伤引起的还是因环境变化造成的。为克服这一缺陷,本文中用概率统计方法,对式(12)表示的损伤指标进行重新定义。
首先在结构完好状态下测得M组Lamb波信号VBi,将其中一组信号(如第1组,i=1)作为基准信号。其余M-1组信号相对于基准信号的损伤指标定义为
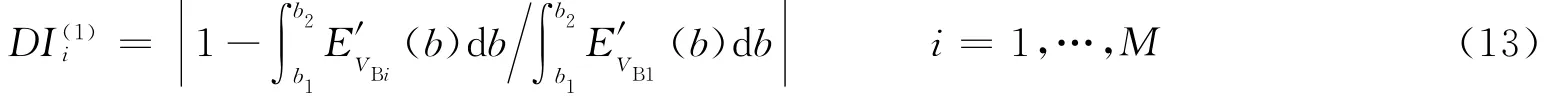
同样地,在结构有损状态下测得N组Lamb波信号VDj,这N组信号相对基准信号的损伤指标定义为
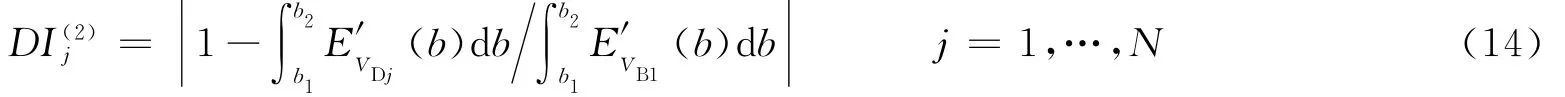
本文中采用概率统计函数t来对上述损伤指标进行统计[14]

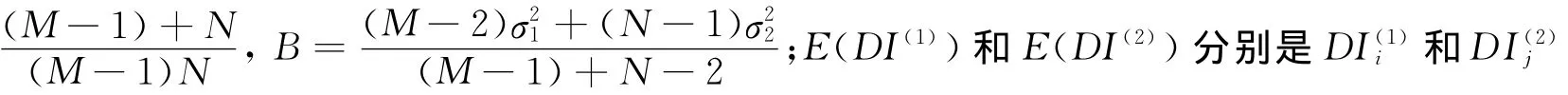
3.2 成像算法
将损伤情况可视化,定量确定损伤的位置,识别损伤的程度一直是结构损伤识别研究的热点问题之一。本文中通过改进T.R.Hay等[16]提出的RAPID(reconstruction algorithm for probabilistic inspection of damage)算法来进行损伤成像研究。以损伤指标代替原算法中的信号差别系数(signal difference coefficient,SDC),改进后算法公式如下
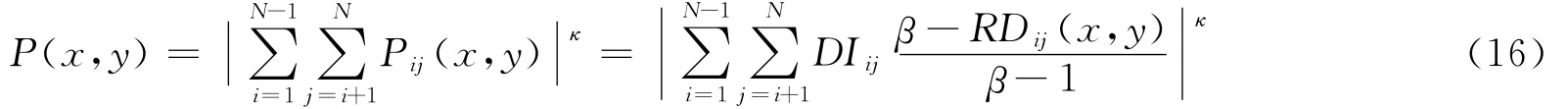
式中:β为尺寸参数,大小为椭圆系最外面椭圆离心率的倒数。在本文中,为提高损伤区域的对比度,引入一个对比增强因子κ。
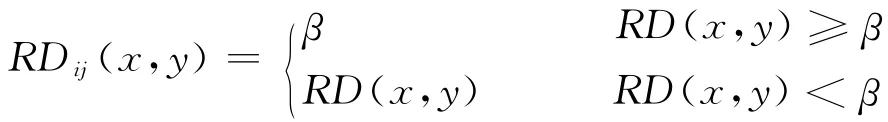
其中
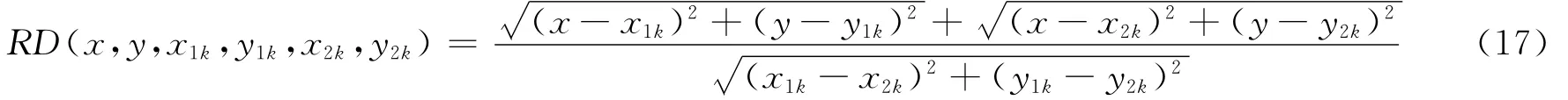
式(17)表示(x,y)坐标处到发射和接收传感器距离之和与发射接收传感器间直接距离之比。图4为传感器通道示意图,当点(x,y)落在椭圆内时,RD(x,y)由式(17)计算得到;而当点(x,y)超出椭圆系范围,取RD(x,y)=β。本文中β=1.02,主要考虑直接路径上的损伤。
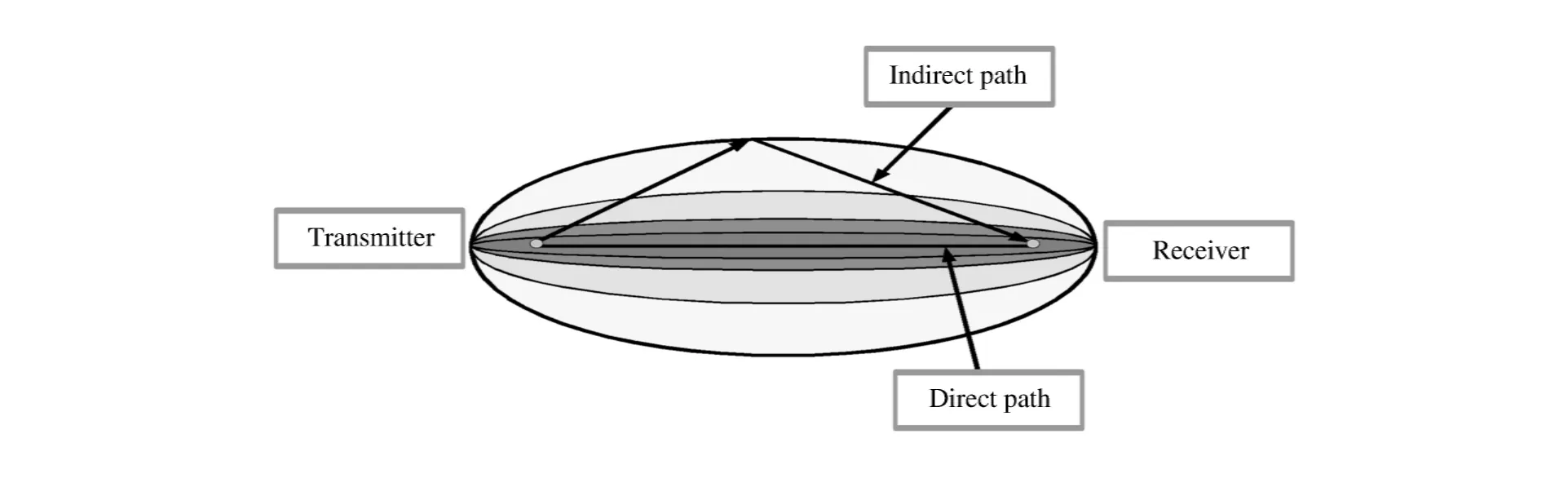
图4 RAPID算法的传感器通道示意图Fig.4Illustrations of the elliptical distribution function of the RAPID algorithm
4 实 验
为验证本文中所提方法的可行性和有效性,建立在实验室条件下的结构健康监测系统,整个系统由NI-PXI 6115数据采集卡和NI-PXI 5412信号发生器组成。试件为碳纤维复合材料板结构,尺寸为250mm×250mm×2mm,在结构中预制冲击损伤,造成复合材料板结构中有纤维断裂和脱层。
采用粘贴在结构表面的压电陶瓷元件来激励和接收应力波信号。在试件表面以板中心为圆心,在直径15cm的圆上均匀布置12个直径12mm、厚1mm的压电传感器S1~S12,组成一个如图5所示的圆形传感器监测网络,用于损伤的监测和成像实验。任意2个压电传感器就可以组成一条激励-接收通道,共有66个激励-接收路径。试件及传感器布置如图6所示。
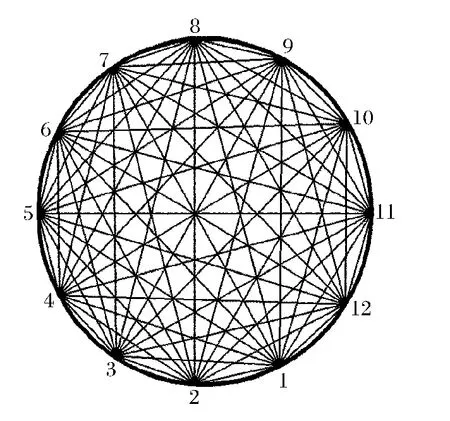
图5 传感器路径示意图Fig.5Diagram of sensing path

图6 复合材料实验件Fig.6Composite plate and PZT
实验中由一个压电传感器在试件中激发窄带Lamb波
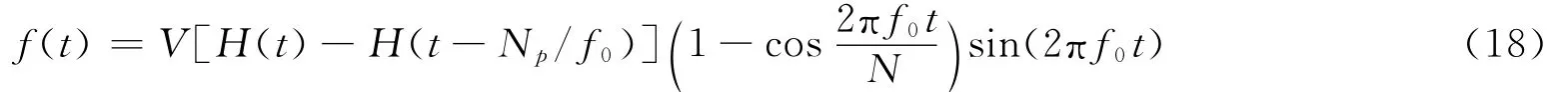
式中:V是信号幅值,H(t)是阶跃函数,Np是峰数,f0是中心频率。实验中窄带波信号的中心频率设定在200kHz。
首先在结构无损伤状态下测得1组Lamb波信号作为基准信号,再每隔0.5h(温度、湿度和噪声等环境发生变化)测量1次,测得10组信号;然后在结构有损伤状态下同样测得10组Lamb波信号作为监测信号,以传感器路径3-9(通过损伤)和路径1-6(未通过损伤)为例,如图7所示。
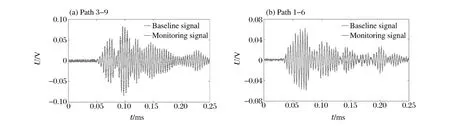
图7 基准及监测状态测得的Lamb波信号Fig.7Captured Lamb wave signals of the reference and present states
运用本文中提出的损伤指标提取方法,采用MP分析手段做预处理。选取150~250kHz这一频带作为尺度,分别对两种状态下的信号进行时频变换,得到信号的局部时间-能量密度,同样以传感器通过损伤路径3-9和未通过损伤路径1-6为例,如图8所示,通道1-6的损伤指标DI=0.026,通道3-9损伤指标DI=0.963。
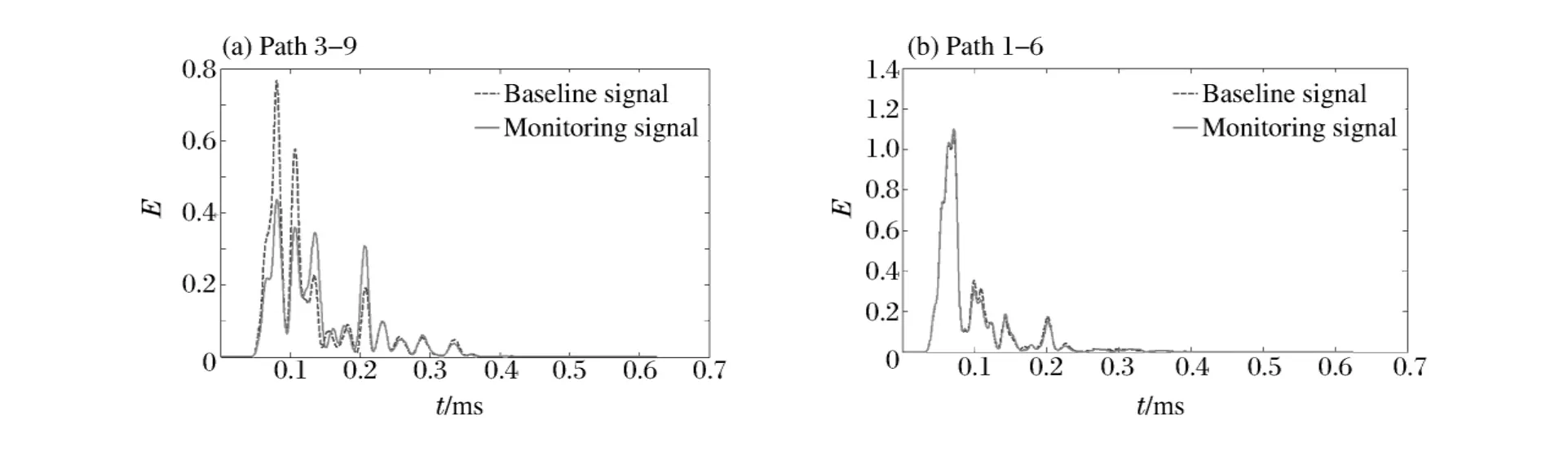
图8 时间-能量密度图Fig.8Diagram of local time-energy density
为了判断损伤指标是由结构损伤引起还是因环境变化造成的,用概率统计方法对每条传感器路径上的损伤指标进行统计分析。实验中,置信度取为0.975,则t0.975=2.4。由此可见,损伤指标是由结构损伤引起的,表1为损伤系数最大的12个通道。

表1 损伤系数最大的12个通道Table 1The maximum damage index of 12paths
将66个损伤指标带入RAPID算法,得到损伤图像。图9(a)、(b)为增强因子κ=1,5时的损伤图像。图中对比度最大的像素点即为识别出的损伤中心位置。图9(c)为超声C扫描的实际损伤图像。通过对比可以看出,该算法得到的损伤图像与实际损伤位置比较接近,得到的损伤图像对比度高,对损伤的指示比较明显。引入的对比度增强因子显著提高了损伤区的相对对比度,大大提高了损伤定位的精度,且具有识别损伤尺寸的潜力。

图9 增强因子κ=1,5时的损伤图像和超声C扫描图像Fig.9The damage image when the image factorκ=1,5and the actual damage image using ultrasonic C scan
5 结 论
对采用压电传感器网络的复合材料结构健康监测系统进行了研究,提出了一种基于Lamb波匹配追踪算法时频处理的损伤概率成像方法。对复合材料结构中的Lamb波信号,使用匹配追踪算法进行时频分析,提取损伤特征值,运用损伤概率成像算法即RAPID算法进行损伤成像,将损伤情况可视化,为定量确定损伤的位置、识别损伤的程度提供一种快速直观的方法,但还需进行深入的研究考虑损伤尺寸对散射lamb波的影响,使得到的损失图像能准确指示损伤的大小和程度。
[1]Giurgiutiu V,Cuc A.Embedded NDE for structural health monitoring,damage detect ion,and failure prevention[J].The Shock and Vibration Digest,2005,37(2):83-105.
[2]Su Z,Ye L,Lu Y.Guided Lamb waves for identification of damage in compo site structures:A review[J].Journal of Sound and Vibration,2006,295(4):753-780.
[3]Wang C S,Chang F K.Diagnosis of impact damage in composite structures with built-in piezoelectrics network[C]∥Proceedings of the SPIE,Smart Structures and Materials.San Diego,CA:SPIE,2000:13-19.
[4]Cawley P,Alleyne D.The use of Lamb waves for the long range inspect ion of large structures[J].Ultrasonics,1996,34(2):287-290.
[5]严刚,周丽.基于Lamb波的复合材料结构损伤成像研究[J].仪器仪表学报,2007,28(4):583-589.
YAN Gang,ZHOU Li.Study on damage imaging for composite structure using Lamb wave[J].Chinese Journal of Scientific Instrument,2007,28(4):583-589.
[6]Hay T R,Wei L,Rose J L,et al.Rapid inspection of composite skin-honeycomb core structures with ultrasonic guided waves[J].Journal of Composite Materials,2003,37(10):929-939.
[7]Howard M M,Lanza di Scalea F.Macro-fiber composite piezoelectric rosettes for acoustic source location in complex structures[J].Smart Materials and Structures,2007,16(4):1489-1499.
[8]Swartz A,Flynn E,Backman D,et al.Active piezoelectric sensing for damage identification in honeycomb composite panels[C]∥Proceedings of 24th International Modal Analysis Conference.Los Alamos National Laboratory,2006.
[9]Ihn J B,Chang F K.Pitch-catch active sensing methods in structural health monitoring for aircraft structures[J].Structural Heath Monitoring,2008,7(1):5-19.
[10]Deng X M,Wang Q,Giurgiutiu V.Structural health monitoring using active sensors and wavelet transforms[C]∥Proceedings of the SPIE,Smart Structures and Integrated Systems.Newport Beach,USA:SPIE,1999:363-370.
[11]Quek S T,Tua P S,Wang Q.Detecting anomalies in beams and plate based on the Hilbert-Huang transform of real signals[J].Smart Materials and Structures,2003,12(3):447-460.
[12]Hong J C,Sun K H,Kim Y Y.Dispersion-based short-time Fourier transform applied to dispersive wave analysis[J].Journal of the Acoustical Society of America,2005,117(5):2949-60.
[13]Mallat S G,Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.
[14]Banerjee S,Ricci F,Monaco E,et al.A wave propagation and vibration-based approach for damage identification in structural components[J].Journal of Sound and Vibration,2009,332(1/2):167-183.
[15]Monaco E,Franco F.Experimental and numerical activities on damage detection using magnetostrictive actuators and statistical analysis[J].Journal of Intelligent Material Systems and Structures,2000,11:567-578.
[16]T R Hay,R L Royer,Huidong Gao,et al.A comparison of embedded sensor Lamb wave ultrasonic tomography approaches for material loss detection[J].Smart Materials and Structures,2006,15(2):946-951.
