基于核Fisher 鉴别分析的手指静脉识别

余成波，张 进，张一萌，李洪兵，2

（1.重庆理工大学远程测试与控制技术研究所，重庆 400050;2.重庆三峡学院，重庆 404000）

0 引言

手指静脉识别技术相比其他的生物识别技术（如指纹识别、虹膜识别、掌纹识别等）具有速度快、安全等级高、活体识别、非接触式等优点，所以它在身份验证、安全系统等方面具有广泛而重要的用途。因此，近年来关于手指静脉识别技术的研究已成为热点之一。

目前手指静脉特征提取的方法主要有两大类:基于结构信息和基于统计特征的特征提取。基于结构信息的特征提取可以分为点特征和线特征两类:点特征数量多，计算量大;线特征提取困难，对相近或相似的手指静脉图片的鉴别力不够。基于统计特征的特征提取方法有:傅里叶变换［1］、Gabor变换［2］、主元分析（principal component analysis，PCA）［3］和 Fisher线性判别（Fisher linear discriminant，FLD）［4］。

Gabor变换和傅里叶变换分析图像时将图像从空域变换到频域，忽略了图像丰富的细节信息，受光照条件影响而产生的不稳定性也较大，且变换后的图像特征仍处于高维空间中。PCA，FLD方法具有特征描述性强、计算速度快、易实现和可分性好等特点，广泛应用于人脸识别、文本识别等许多领域。但是PCA提取的特征是最佳描述特征而不是最佳分类特征，不利于分类匹配。而Fisher线性判别［5］的基本思想是找到模式变换以后使得类内距离最小和类间距离最大的投影方向，从而提取最佳分类特征。

在提取小样本的高维手指静脉图像特征时，由于光照、温湿度、水平位移等因素的影响使得采集的静脉图像是非线性分布的，因此引入核方法将Fisher算法进一步拓展到非线性的情况，提出了核Fisher算法（kernel Fisher discriminant analysis，KFDA）。核Fisher判别分析使用了类似于支持向量机（support vectormachine，SVM）［6］和核 PCA 方法的“核技巧”，即首先把数据非线性地映射到某个特征空间F，然后在这个特征空间中进行Fisher线性判别，这样就隐含地实现了原输入空间的非线性判别。核Fisher算法在处理非线性数据方面比Fisher算法有了更大的进步。

1 Fisher线性判别

Fisher线性判别是一种经典的分类算法，它是依据使类间的离散度最大和类内的离散度最小的原则，以此来确定原始向量的投影方向，使各类别之间达到最大程度的分离，从而实现正确的分类。Fisher算法的线性判别函数W（x）的形式［7］为

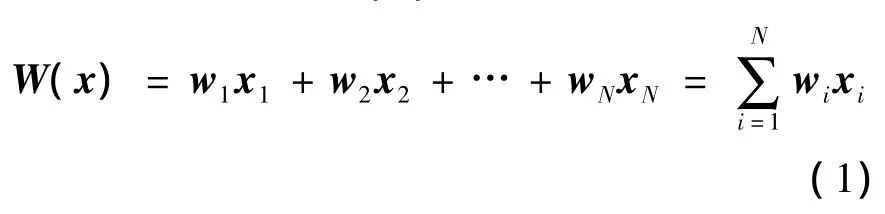
（1）式中:wi（i=1，2，…，N）为不相同的N个模式类;xi（i=1，2，…，N）表示同一模式类中i个不同的个体。判别系数就是投影 w=（w1，w2，…，wN）T。

各类样本的均值向量为mi（i=1，2，…，N），且

（2）式中:Ni为wi类的样品个数;xij为第i类中的第j个样本。

类间样本离散度矩阵Sb和类内样本离散度矩阵Sw分别可定义为

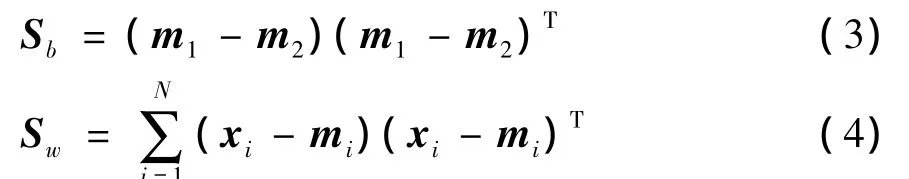
根据类间离散度最大、类内离散度最小原则，可得出 Fisher鉴别函数定义［11］为

最后投影向量w满足（Sb－λSw）w=0，求得满足该式的最大特征值λ0对应的特征向量w0，则判决函数［7］为

（6）式中，x为需要鉴别的未知样品向量。

2 基于核Fisher判别的手指静脉识别

Fisher线性判别解决问题的关键就是寻找一个最优的映射方向，而对手指静脉图像而言，数据分布呈非线性，线性判别显得过于简单，并不能达到最好的分类效果。因此在手指静脉识别系统中提出使用基于核函数的Fisher判别进行分类。

2.1 核Fisher判别的核心思想

核Fisher判别的核心思想是，通过一个非线性映射Φ将原始特征空间映射到一个新的特征空间H，在新的特征空间H中使用Fisher线性判别进行分类。KFDA是Fisher线性判别的非线性扩展，可以很好地对非线性数据进行分类，系统框图如图1所示。

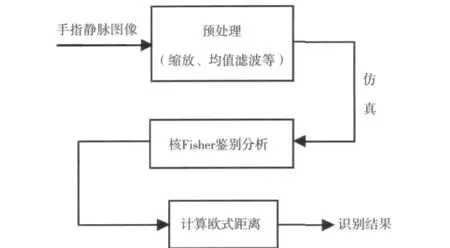
图1 手指静脉识别系统框图Fig.1 Block diagram of the Finger vein identification system

2.2 核Fisher算法的实现

手指静脉识别过程分为2个部分:第1部分是样本训练过程;第2部分是样本的测试过程。核Fisher算法主要应用在样本的训练阶段。

设数据库中每个人的静脉图像w1，w2，…，wp作为p个不同的模式类，第i类样本数为Ni，X={X1，X2，…，XNi}表示第i类样本，总的训练样本数为N。则原输入空间X到新的特征空间H的非线性映射为Φ:X→H。

此时核Fisher鉴别函数可定义为

在新的特征空间H中的类间离散度矩阵SΦb和类内离散度矩阵SΦw分别为

由于在空间H中得到的矩阵维数非常高，直接求解是不可能的，因此可以通过核函数的技巧，这样就避免进行了非线性运算。

考虑到任何一个目标函数的解w都可以用特征空间中元素的线性组合 Φ（X1），Φ（X2），…，Φ（XN）表示

（11）式中，αi为各个元素Φ（Xi）的线性系数。因此结合（10）式和（11）式，可得

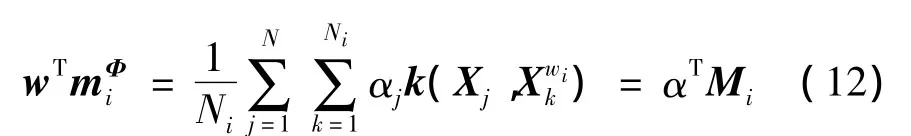
根据（8）式和（9）式可得

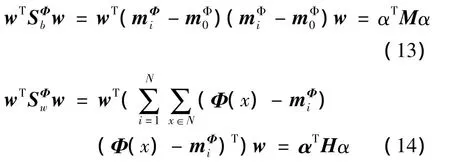
则（7）式可变为

特征空间Φ（x）在α上的投影μ为

3 手指静脉数据库建立与预处理

3.1 手指静脉数据库

目前，对于人脸识别已经形成了许多标准的数据库，而由于对手指静脉识别的研究起步较晚，因此国内外还没有建立起通用的手指静脉数据库。

为了对手指静脉图像进行预处理分析，所在实验室建立了手指静脉数据库。该数据库由50个不同人的手指静脉图像组成，而且对每个人在不同时间和光照条件下采集了10幅不同的图像。所有图像都有一个黑色的背景，手指是竖直向上（能容许一定的位置偏移），这些图像大小为（328×376）。图2所示为数据库中不同3人手指静脉图像和同一人的不同3幅手指静脉图像。

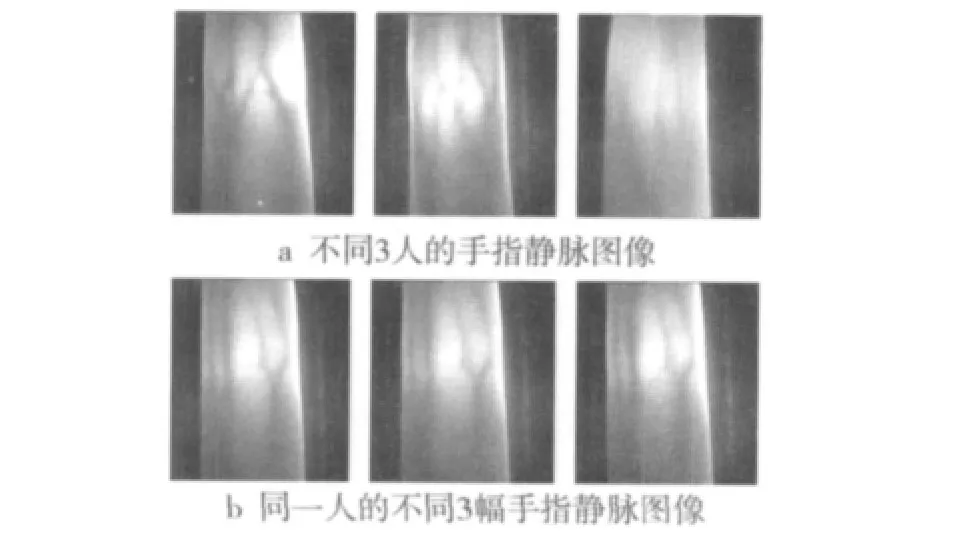
图2 手指静脉图像Fig.2 Finger vein images

3.2 手指静脉图像的预处理

如果直接将采集装置得到的图片运用本文的算法来进行分类识别，其识别精度会产生较大的误差，因此需要对图片进行预处理。

1）图像缩放。采集到的图像尺寸维数过大，为了后续处理的方便，并且也为了缩短识别时间，需要按照一定比例对图像进行统一的缩放，本文是将大小为（328×376）的图像缩小为（97×65）。

2）灰度归一化。尺寸缩小后的静脉图像灰度分布还是很集中，不利于特征提取与分类。因此采取线性灰度调整的方法，将灰度能量聚集于［C1，C2］图像灰度归一化到［0，255］范围，得到灰度分布均匀的图像 f（i，j）［8］

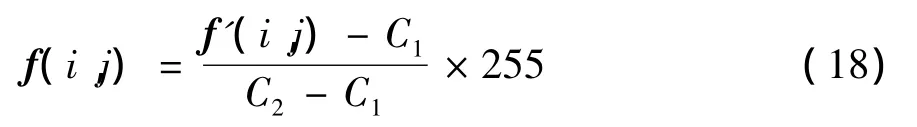
（18）式中:f'（i，j）表示原图灰度值;f（i，j）表示变换后的灰度值;C1表示原图最小灰度值;C2表示原图最大灰度值。

3）均值滤波［9］。由于光照强度、温湿度对采集装置的影响而使得图像存在一定的噪声，为了提高算法识别准确度，需要对噪声进行滤波。采取常用的均值滤波方法对图像进行平滑去噪处理，其基本原理是用均值代替原图像中的各个像素值，即对待处理的当前像素点（m，n），选择一个模板，该模板由其近邻的若干像素组成，求模板中所有像素的均值，再把该均值赋予当前像素点（m，n），作为处理后图像在该点上的灰度 p（m，n），即 p（m，n）=为该模板中包含当前像素在内的像素总个数。任意h，p两人的原始图像与经过预处理后的图像对比效果如图3所示。

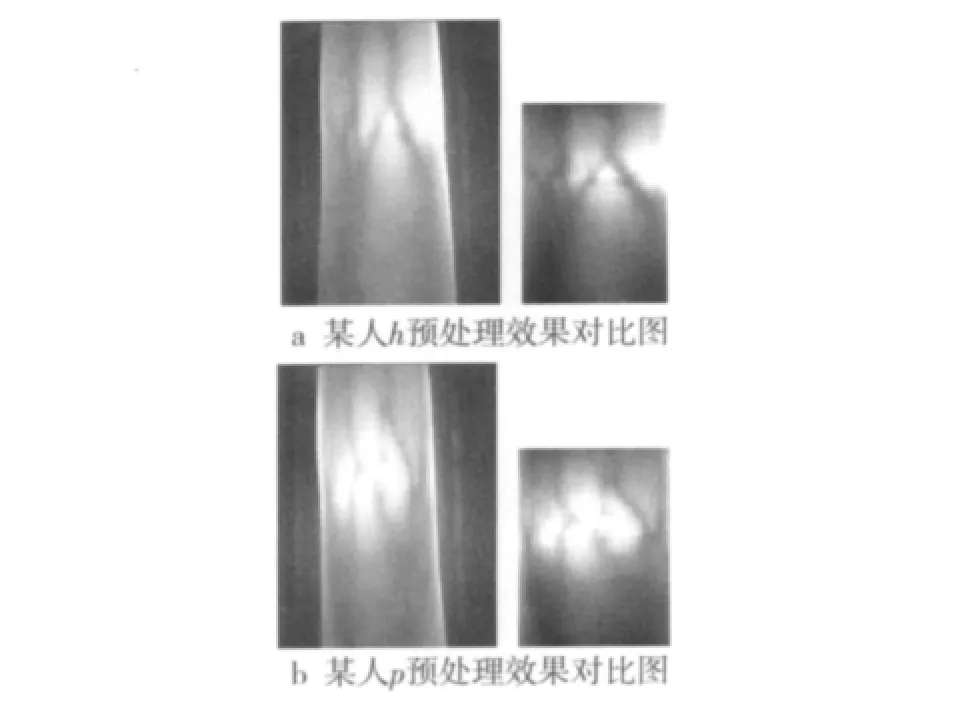
图3 原始图像与预处理后图像对比图Fig.3 Omparison chart between the original image and the pretreatment image

4 实验结果与分析

为检验本文方法对抽取小样本手指静脉图像分类识别的有效性，通过采集装置得到的图像经过预处理后的数据库进行了测试，实验环境为Inter 1.60 GHz，内存为1 GByte，Matlab 7.1仿真。实验时，将50个人的500幅图像随机分成2组，一组作为训练样本，一组作为测试样本。此时，选每人的前k幅图片作为训练样本，后10－k幅图片作为测试样本，两组之间的样本没有重叠，即测试样本不包含在训练样本中。图4为本文算法分别选用3种不同的核函数得到的仿真图，3种核函数形式主要为

①二次核函数［10］

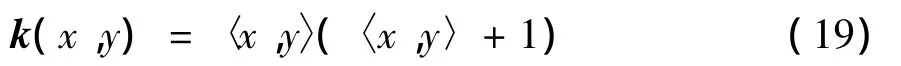
②多项式核函［11］

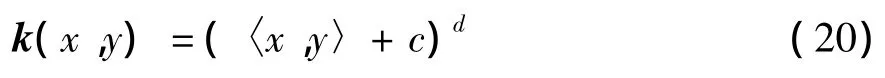
（20）式中:c为常数;d为多项式阶数。

③高斯径向基（radial basis function，RBF）核函数［12］

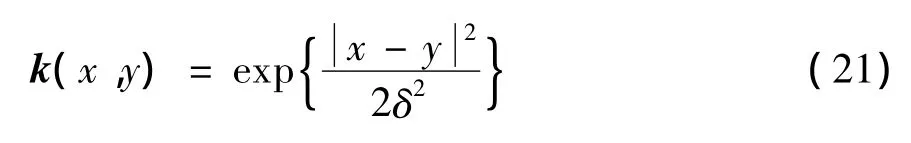
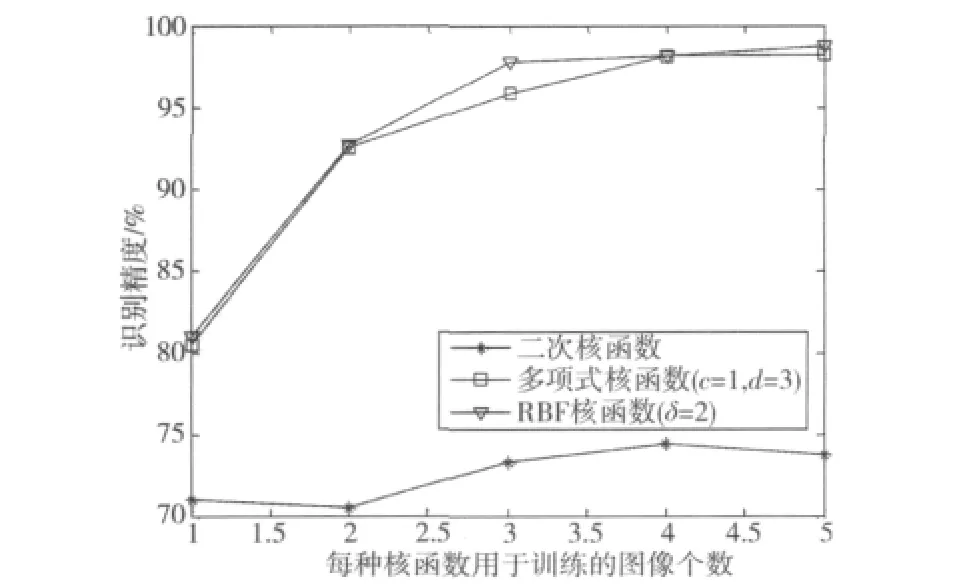
图4 3种核函数识别效果对比图Fig.4 Comparison chart of three kinds of kernel function

从图4可以看出由于二次核函数只对于线性数据的分类效果较好，而本文的数据呈现非线性的特征，因此在仿真时其识别精度比较低，多项式核函数（c=1，d=3）和RBF核函数（δ=2）的识别精度都远远高于二次核函数。

本文算法的识别性能如表1所示。结合图4以看出，选用RBF核函数的仿真时间会明显高于多项式核函数，而两者的识别精度几乎大致相同。因此，本文算法就直接选用了多项式核函数。

本文方法在选取了多项式核函数，训练样本数和测试样本数分别为5的情况下，通过计算待识别手指图像的投影矩阵与各测试样本的聚类中心之间的欧式距离，得到识别结果的过程如表2所示。

表1 基于KFDA方法的3种核函数的识别性能Tab.1 Recognition performance of the three core functionswhich are based on KFDA approach

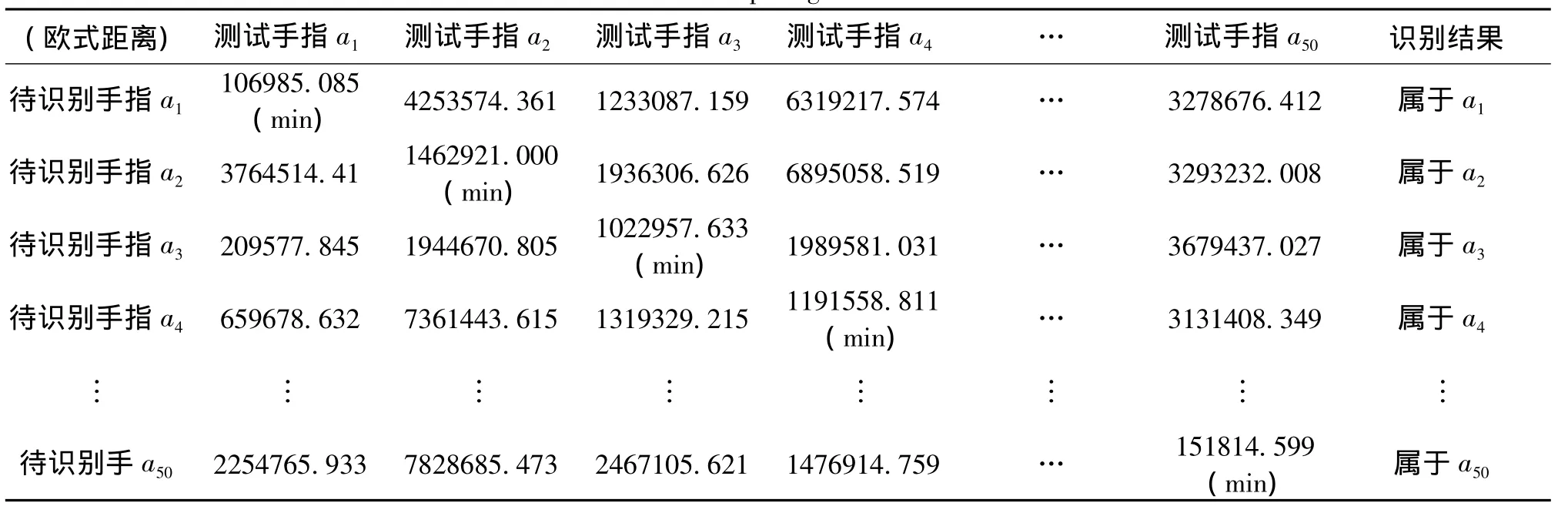
表2 计算欧式距离测试过程Tab.2 Test of computing euclidean distance

图5是在不同的训练样本数目下运用PCA，KPCA，FLD，KFDA等4中不同方法的仿真图对比图，从识别率比较发现，随着测试样本数的增加，各种方法的识别精度呈上升趋势，但KFDA方法的识别效果明显优于其他方法，在训练样本数为5的情况下本文方法识别精度达到了98.2%。

图5 4种算法在不同训练样本下的识别精度Fig.5 Recognition accuracy of the four algorithmswhich are under different training samples

5 结论

本文引入了核方法，将高维空间的不可分问题转化成了低维空间的线性可分问题，并且利用了类间散度阵和类内散度阵作为Fisher准则，通过对建立的小样本手指静脉数据库进行实验测试，计算投影矩阵与各测试样本的聚类中心之间的最小欧式距离进行识别判断。实验结果表明，基于多项式核函数的KFDA方法具有易实现，测试识别时间较短，识别精度较高等优势。

［1］ZHOU Xin，WU Ying.Application of Kernel Fisher Discriminant Analysis to Digital Signal Classification［J］.Journal of Beijing University of Posts and Telecommunications，2011，34（1）:35-39.

［2］ 边肇棋，张学工.模式识别［M］.北京:清华大学出版社，2000.

BIAN Zhao-qi，ZHANG Xue-gong.Pattern Recognition［M］.Beijing:Tsing Hua University Press，2000.

［3］ MOGHADDAM B，JEBARA T，PENTLAND A，Bayesian face recognition ［J］.Pattern Recognition，2000，33（11）:1771-1782.

［4］杨健，杨静宇，叶晖.Fisher线性鉴别分析的理论研究及其应用［J］.自动化学报，2003，29（4）:481-493.

YANG Jian，YANG Jing-yu，YE Hui.Theory of Fisher Linear Discriminant Analysis and Its Application［J］.Acta Automatica Sinica，2003，29（4）:481-493.

［5］郑宇杰，杨静宇，徐勇，等.一种基于Fisher鉴别极小准则的特征提取方法［J］.计算机研究与发展，2006，43（7）:1201-1206.

ZHENG Yu-jie，YANG Jing-yu，XU Yong，et al.A New Feature Extraction Method Based on Fisher Discriminant Minimal Criterion［J］.Journal of Computer Research and Deverlopment，2006，43（7）:1201-1206.

［6］ 杨勇，罗飞.基于粗糙集理论的表情识别研究［J］.重庆邮电大学学报:自然科学版，2009，21（4）:549-554.

YANG Yong，LUO Fei.Facialexpression recognitionbased on rough set theory［J］.Journal of Chongqing University of Post and Telecommunications:Natural Science Edition，2009，21（4）:549-554.

［7］ 杨淑莹.模式识别与智能计算［M］.北京:电子工业出版社，2008.

YANG Shu-ying.Pattern Recognition and Intelligent Computing［M］.Beijing:Publishing House of Electronics Industry，2008.

［8］ DAVID M J，TAX D M J，KITTLER J.Combining Multiple Classifiers by Averaging or by Multiplying［J］.Pattern Recognition，2000，33（9）:1475-1485.

［9］ 余成波，张睿，秦华锋.基于CCD的手指静脉身份识别系统的研制［J］.半导体光电，2008，9（3）:483-485.

YU Cheng-bo，ZHANG Rui，QING Hua-feng.Development of An IdentityRecognition System Based on CCD Finger Vein Image［J］.Semiconductor Optoelectronics，2008，9（3）:483-485.

［10］ SU C L.Face recognition by Using characteristic matrix and ring rotation invariant transform［J］.Mathematics and Computation，2007，189（1）:116-125.

［11］ SHU Yang，SHUICheng-yan，CHAO Zhang.Bilinear analysis for kernel selection and nonlinear feature extraction［J］.IEEE Transactions on Neural Networks，2007，18（5）:1442-1452.

［12］MARIAN SB，JAVIER R M，TERRENCE JS L.Face recognition by independent componentanalysis［J］.IEEE Transactions on Neural Networks，2002，13（6）:1450-1464.