一种基于ECDLP有身份认证的ECDH 密钥协商方案

曹 阳，郝玉洁，洪 歧

（1.陕西理工学院计算机系，陕西汉中723000;2.电子科技大学计算机学院，四川成都 610051）

0 引言

密钥协商方案（key agreement scheme）就是一种能够让通信双方或多个参与方在一个公开的、不安全的信道上，通过通信协议协商建立一次会话所用的临时密钥的密码协议。椭圆曲线密钥协商方案（elliptic curve key agreement scheme-diffie-hellman version，ECDH）［1-2］是椭圆曲线密码体制［3］中常用密钥协商方案之一，已被列入IEEE1363-2000和ANSIX9.63等标准之中。它能较好地防止被动攻击，但无法应付所谓的中间人攻击。M.Aydos等［4］提出采用证书实现可认证的密钥交换，能防止中间人的攻击，但此方案需要通过第三方可信认证中心CA来完成，且终端能够处理证书，系统扩展存在较大的难度，当用户增多时需要增加存储空间来存储证书，同时也要增加带宽来验证证书。Seo等［5］提出基于共享口令可认证的Diffie-Hellman密钥协商协议，但该方案容易遭到离线口令猜测、服务器欺骗及字典攻击。为了解决上述问题，本文提出一种基于椭圆曲线离散对数问题（elliptic curve discrete logarithm problem，ECDLP）的有身份认证的密钥协商方案。

1 椭圆曲线密码体制

1.1 椭圆曲线

所谓椭圆曲线［6-7］指的是由韦尔斯特拉斯（Weierstrass）方程所确定的平面曲线

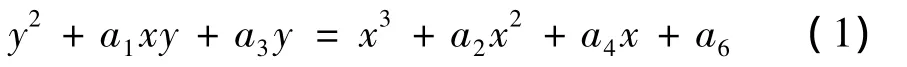
（1）式中:系数ai（i=1，2，…，6）定义在某个域上，可以是有理数域、实数域、复数域，还可以是有限域GF（q）;x，y是椭圆曲线上的点，椭圆曲线密码体制中用到的椭圆曲线都定义在有限域上的。

常用的有限域GF（q）上的方程定义为y2=x3+ax+b的椭圆曲线E（GF（q）），其中，a，b∈GF（q）且4a3+27b2≠0（modp），p为大于3的素数。

1.2 椭圆曲线离散对数问题及椭圆曲线选取

椭圆曲线公钥密码体制的安全性［8-9］与相应的ECDLP的求解困难性等价，困难性是所有椭圆曲线密码方案安全性的基础。ECDLP定义为给定椭圆曲线E（GF（q））及其上一点P，n为P点的阶，对于另一点Q∈E（GF（q）），求整数l（0≤l≤n－1），使得Q=lP（假设整数l存在），其中，l称为Q的以P为底的离散对数。椭圆曲线上所有的点，外加一个无穷远点构成的集合连同其上定义的加法运算构成一个Abel群。在Abel群E（GF（q））上关于m（m是明文消息）的方程Q=mP中，已知m和点P求点Q比较容易，反之，已知点Q和点P求m却是相当困难，这个问题称为椭圆曲线上点群的离散对数问题，椭圆曲线密码体制正是利用这个困难问题设计而来。安全椭圆曲线的选取方法主要有虚数乘法和随机选取2种方法，从安全角度考虑，本文采用随机选取方法选取椭圆曲线。

1.3 明文嵌入

通常加密系统都需要让原文变为可以进行数学计算的数值，在椭圆曲线密码体制中，需要将明文以一定的方式映射为椭圆曲线上的点，一个点由X坐标和Y坐标组成，因此，一个点实际上是由2个数组成的数对，并且这2个数都在曲线所在的有线域GF（q）上。由于一个点由2个数组成，而消息可以转换成一个数，因此必须找到另外一个数与消息转换后得到的数组成一个点。这就是所谓的明文消息的嵌入。明文嵌入概率算法描述如下。

1）假设明文消息是m（0≤m≤M），k是一个足够大的整数，使得将明文消息镶嵌到椭圆曲线上时，错误的概率是2－k。

2）计算x={mk+j，j=0，1，2，…}={30m，30m+1，30m+2，…}，直到x3+ax+b（modp）是平方根，即得到椭圆曲线上的点 （x，，其中，k可以在30～50取值，不防取k=30，m是明文消息。

3）从椭圆曲线上的点（x，y）得到明文消息m，只须求m=x/30。

2 ECDH密钥协商

ECDH 密钥协商［10］是 Diffie-Hellman［11］密钥协商协议在ECC上的实现。假设需要完成密钥协商通信双方为A和B，ECDH密钥协商协议描述如下。

1）A随机地选择一个大整数kA∈［1，n－1］作为自己的私钥，并计算公钥QA=kA P发送给B;

2）B随机地选择一个大整数kB∈［1，n－1］作为自己的私钥，计算公钥QB=kB P发送给A;

3）A在收到B发来的QB以后，计算

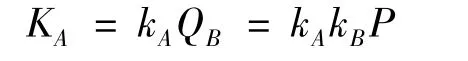
同样，B在收到A发过来的QA后，计算

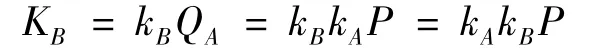
这样，A和B完成了ECDH密钥协商，协商后双方约定的临时会话密钥为K=kA kB P。

总之，田面水中各形态氮浓度在施肥后 1~4 d达到峰值，在施肥后10 d内浓度较高，若在此期间遇到强降雨，稻田氮素的流失量会随着施氮量的增加而增加，故施氮初期是管理氮素流失的关键时期。施用控释氮肥处理田面水各形态氮浓度比施用尿素处理有所降低，一定程度上减少了氮素流失的风险。

3 基于ECDLP有身份认证的ECDH密钥协商方案

从基于ECC Diffie-Hellman密钥协商协议可以看出，通信双方A或B在向对方发送信息时容易受到中间人的攻击，在密钥协商中，任何人都可以获得公钥，中间人E选择大整数kM∈［1，n－1］，截取A发送给B的kAP和B发送给A的kB P，并将kAP，kB P修改为kM P，协商结束后，A与攻击者生成共享密钥kA kB P，但A误认为B共享的，B与攻击者共享了密钥kA kB P，而B却误认为是与A共享的，真正的用户A与B并没有共享一个密钥。当用户A发送机密信息给B时A用kA kM P对消息加密，攻击者截获进行解密，然后伪造一个消息，用密钥kA kB P加密后发送给B，这样，攻击者成功的欺骗了用户A，B，而用户A，B却并不知道，这影响了正常的密钥协商。

为了使A，B双方能够正常通信，完成正常的密钥协商，在此建立一个有身份认证机制的密钥协商方案，该方案描述如下。

假设q是大于3的素数，在有限域GF（q）随机生成一条椭圆曲线E（GF（q）），使得求解ECDLP在计算上是不可行的。随机选取一点G，G的阶p是一大素数。通信双方各自选择自己的整数k（1≤k≤p－1），计算k关于p的k－1，将k和k－1作为自己的秘密密钥，而将Q=kG作为自己的公开密钥。设A和B进行密钥协商身份认证过程如下。

1）A随机选取秘密数s，并计算s关于p乘法逆元s－1，保密s和s－1，计算GA=sQA，把自己的身份信息IA和GA一并发送给B;

2）B收到IA和GA，用自己的秘密密钥加密GA得到GB=kBGA，并把GB发送给A;

3）A收到GB后，计算X=s－1kA－1GB=kBGX，并把X与B公开的QB进行比较，如果相等则确定对方就是B，并把（X1，X2）发送给B，X1=kA－1GB=kBsG，X2=（kA+s）G;否则放弃通信;

4）B收到（X1，X2）后，计算Y1=kB－1X1=sG，Y=X2+（－Y1）=kAG，把Y与A公开的秘密密钥QA进行比较，如果相等而相信对方就是A，否则放弃通信。身份认证过程如图1所示。

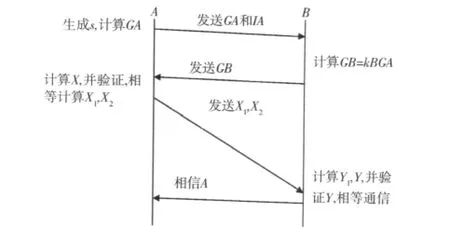
图1 身份认证过程Fig.1 Authentication process

1）A随机选择整数nA∈［1，n－1］，利用B的公钥计算SA，并将SA发送给B，收到B的SB后计算:

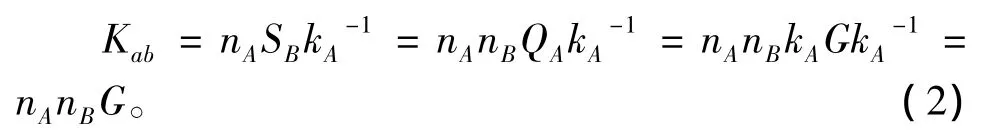
（2）式中:kA是A的私钥;QA是A的公钥;G是E（GF（q））上的一点。

2）B随机选择整数nB∈［1，n－1］，利用A的公钥计算SB并将SB发送给A，收到A的SA后计算:

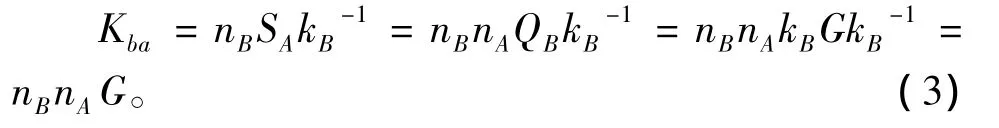
（3）式中:kB是B的私钥;QB是B的公钥;G是E（GF（q））上的一点。

从上可以看出，在身份认证的条件下A和B进行密钥协商，且双方能得相同的密钥。

4 安全性分析

可以看到，安全椭圆曲线选取保证了求解ECDLP是计算上不可行的，以下从4方面对本文提出的密钥协商方案进行安全性分析。

1）该方案实现了A和B之间的双向身份认证，攻击者不能冒充通信双方中的任何一方，增强了双方通信的安全性。假设攻击者可以冒充A，但由于不知道s和kA，因此无法生成（X1，X2），B也就无法通过计算得到与A相同的公钥，同样攻击者也不能冒充B，进而身份认证失败。

2）密钥安全性，通信双方在进行密钥协商之前，都是在双向身份认证通过的前提下进行的，加上密钥协商时nA nB是随机选取的，也就使得攻击者法从一个已知的会话密钥推出将来可能的会话密钥，因此密钥是安全的。

3）前向安全性，信道上传输的信息:GA，GB，（X1，X2），基于ECDLP这一难题，攻击者无法从中恢复nA，nB，所以nA，nB依然是安全的。

4）防止重放攻击，因为nA，nB都是随机选取，可以保证信息的新鲜性，通信双方在密钥协商的时候也就确认了密钥是本次协商得到的。

5 总结

本文给出了一种基于ECDLP有身份认证的ECDH密钥协商方案，其安全性是建立在椭圆曲线离散对数问题困难性的基础上之上。该方案分为认证和协商两个过程，在身份认证中，参数s，kA，kB都是保密的，因而攻击者无法冒充A或B，从而保证了身份认证的正确性。在密钥协商阶段也使用了随机数nA，nB，从而保证了密钥协商的安全性，同时还可以防止重放攻击。

［1］ LAW L，MENEZESA，QU M，et al.An efficient protocol for authenticated key agreement［J］.Designs，Codes and Cryptography，2003，（3）28:119-134.

［2］SMART N P.An identity based authenticated key agreement protocolbased on the well pairing［J］.Electronics Letters，2002，38（13）:630-632.

［3］KOBLITZ N.Elliptic Curve Cryptosystem［J］.Mathematics of Compution，1987，48（177）:203-309.

［4］ AYDOSM，SUANR B，KOC C K.An elliptic curve cryptography based authentication and key agreemend protocol forwireless communication［J］.Electronics Letters，1999，35（13）:82-85.

［5］DONG Hwi-seo，SWEENEY P.Simple authenticated key agreement algorithm［J］.Electronics Letters，1999，35（13）:1073-1074.

［6］黄剑樱.浅析椭圆曲线密码体制［J］.宜宾学院学报，2007，6（6）:88-89.

HUANG Jian-ying.Introduction of Elliptic Curve Cryptography［J］.Journal of Yibin University，2007，6（6）:88-89.

［7］ 曹阳.基于无线局域网认证中ECC密码体制的应用研究［D］.成都:电子科技大学，2008:16-24.

CAO Yang.Applied Research of Elliptic Curve Cryptography Based on Wireless LAN Certification［D］.Cheng du:University of Electronic Science and Technology，2008:16-24.

［8］刘志猛，赵燕丽，范辉.椭圆曲线密码体制中安全曲线的选取［J］.淮海工学院学报，2008，17（1）:25-28.

LIU Zhi-meng，ZHAO Yan-li，FAN HUI.Selection of Elliptic Curves Based on ECC［J］.Journal of Huaihai Institute of Technology，2008，17（1）:25-28.

［9］ 汪朝晖.椭圆曲线密码的安全性研究［D］.武汉:武汉大学，2004:27-28.

WANG Chao-hui.A Research on the Securities of Elliptic Curve Cryptosystems［D］.Wu han:Wuhan University，2004:27-28.

［10］邵晓博.椭圆曲线密码体制中密钥协商方案改进的研究［J］.计算机安全，2010，01:23-25.

SHAO Xiao-bo.Reserach of Improved Key Agreement Scheme Based on Elliptic Curve Cryptography［J］.Computer Security，2010，01:23-25.

［11］隋爱芬，杨义先，钮心忻，等.基于椭圆曲线密码的可认证密钥协商协议的研究［J］.北京邮电大学学报，2004，27（3）:28-32.

SUI Ai-fen，YANG Yi-xian，NIU Xin-xin etc.Reserach on the Authenticated Key Agreement Protocol Based on Elliptic Curve Cryptography［J］.Journal of Beijing University of Posts and Telecommunications，2004，27（3）:28-32.