抗多普勒频移的Ka频段FRFT-OFDM 系统及其均衡

申 勇，达新宇，曾 武，谢铁城

（空军工程大学电讯工程学院，陕西西安 710077）

0 引言

Ka频段（20～30 GHz）频率资源丰富，可用带宽理论上可达3.5 GHz，是理想的宽带卫星通信频段。多载波正交频分复用（orthogonal frequency division multiplexing，OFDM）凭借其结构简单，频谱利用率高和抗频率选择性衰落的特点，成为实现Ka频段移动卫星通信高速数据传输的良好方式［1-3］。然而，地球站与卫星之间的相对运动会产生严重的多普勒频移［4-6］，使得Ka频段移动卫星信道呈现明显的时变特性，从而破坏了传统OFDM系统中子载波间的正交性，形成严重的子载波间干扰（inter carrier interference，ICI）。文献［7-10］虽然对 Ka频段移动卫星信道模型进行了比较详细的研究，但没有就多普勒频移对信道造成的影响提出具体的处理方法。

由于分数阶傅里叶变换（fractional Fourier transform，FRFT）具有较强的时频分析能力［11］与相对成熟的快速算法［12］，因此本文利用 FRFT代替传统OFDM系统中的FFT，在选择最优变换阶次的基础上，对Ka频段FRFT-OFDM系统进行了均衡，有效降低了不同环境条件下多普勒频移对系统造成的影响，保证了数据的高速可靠传输。

1 Ka频段移动卫星信道模型

影响Ka频段移动卫星通信的因素主要包括固定链路衰减（降雨衰减、大气吸收等）和移动因素衰减（多径衰落、阴影衰落和多普勒频移）2种。

1.1 固定链路衰减

本环境下信号包络r和相位φ的概率均为高斯分布，其概率密度函数（probability density function，PDF）可分别表示为［7-8］

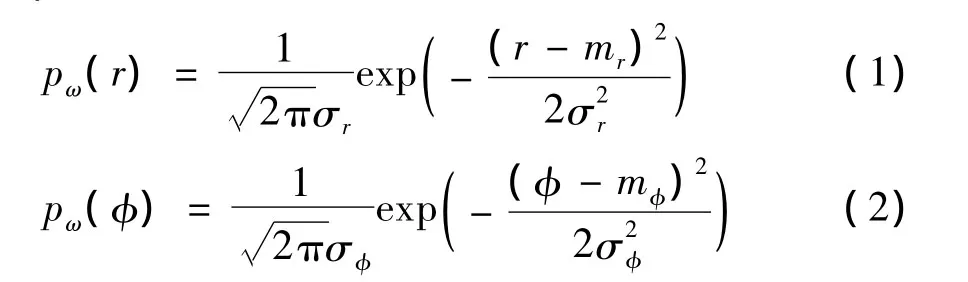
（1）—（2）式中:σ2r和σ2φ分别为不同天气下信号包络和相位的方差;mr和mφ分别为相应均值。

1.2 移动因素衰减

本环境下，信号包络r的PDF为［9-10］

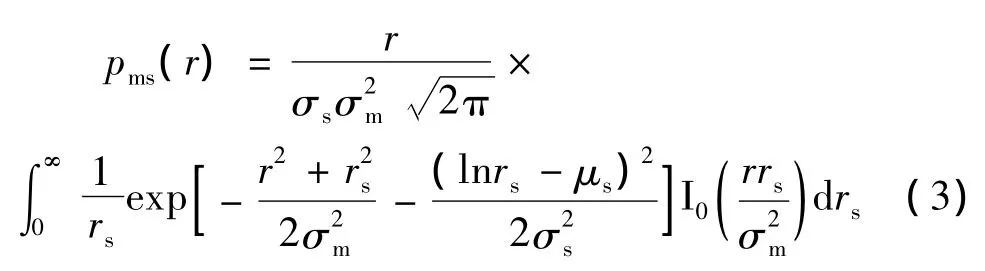
（3）式中:rs和μs分别表示阴影效应下的信号包络及其均值;σm和σs表示多径与阴影效应下信号包络对应的方差;I0（.）表示零阶修正贝塞尔函数。而其相位θ可近似服从高斯分布

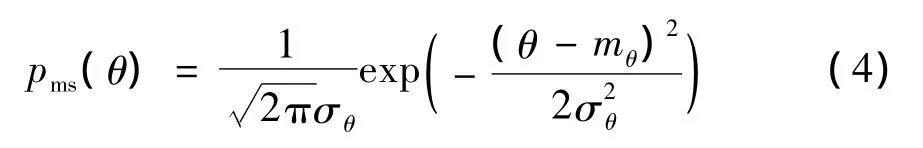
（4）式中，mθ和σθ分别表示相位的均值和方差。

严重的多普勒频移会影响Ka频段移动卫星通信系统的通信质量，因此需要在上述信道模型中引入一个多普勒频移分量fd。同时，由于接收端的运动速度相对较低［5］，所以fd可认为是一个固定值，从而可建立如（5）式所示的移动因素影响下的信道模型。

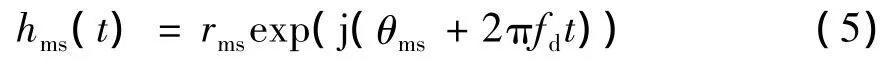
（5）式中，rms和θms分别表示信号的包络与方差。

1.3 Ka频段移动卫星信道综合模型

图1是本文提出的引入多普勒频移分量之后的Ka频段移动卫星信道综合模型。

由图1可知，信道综合模型可以表示为

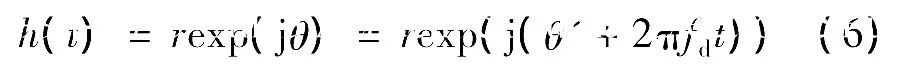
（6）式中，接收信号包络r在特定大气衰减ω条件下的PDF为

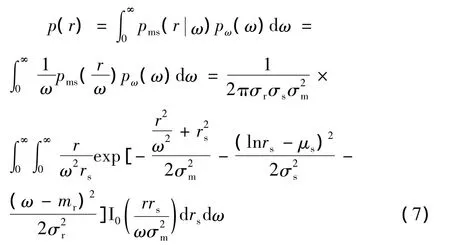
图1 Ka频段移动卫星信道综合模型Fig.1 Model ofmobile satellite channel in Ka-band

接收信号的相位θ=θ'+2πfdt，其中，θ'由φ和θms组成，因为二者均服从高斯分布且相互独立，所以θ'同样服从高斯分布。

2 Ka频段FRFT-OFDM系统

结合上述信道模型，可建立如图2所示的Ka频段FRFT-OFDM系统框图。

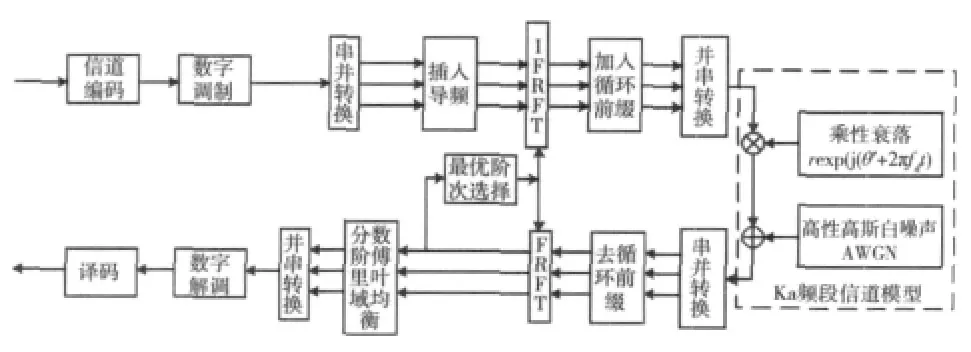
图2 Ka频段FRFT-OFDM系统框图Fig.2 Block diagram of FRFT-OFDM in Ka-band

2.1 最优阶次选择

假设 x=［x（0），x（1），…，x（N－1）］T是一个Ka频段中 OFDM 符号 s=［s（0），s（1），…，s（N－1）］T需要传输的数据，则结合文献［11］可将接收信号y表示为

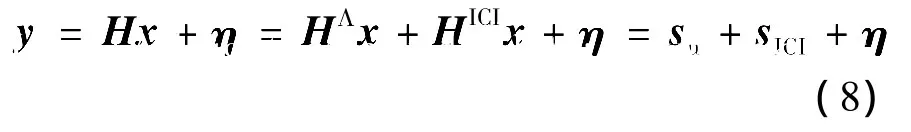
（8）式中:H为Ka频段信道在FRFT域的转移矩阵;H∧和HICI分别对应H对角线上和对角线以外元素组成的矩阵;su与sICI分别对应有用信号和子载波间干扰信号;η为长度为N的AWGN向量。

为使ICI信号与有用信号具有最小能量比值，Ka频段FRFT-OFDM系统最优阶次选择的目标函数可表示为

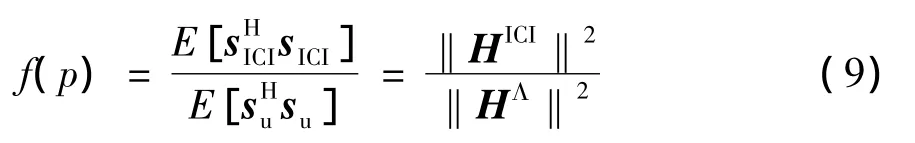
（9）式中，‖·‖表示矩阵的Frobenius范数。因此可以将（9）式取最小值时的p作为系统的最优变换阶次。

2.2 信道均衡

设乘性滤波器用U=diag（un，n）表示，其中n=0，1，…，N－1，则均衡之后的接收信号可以表示为

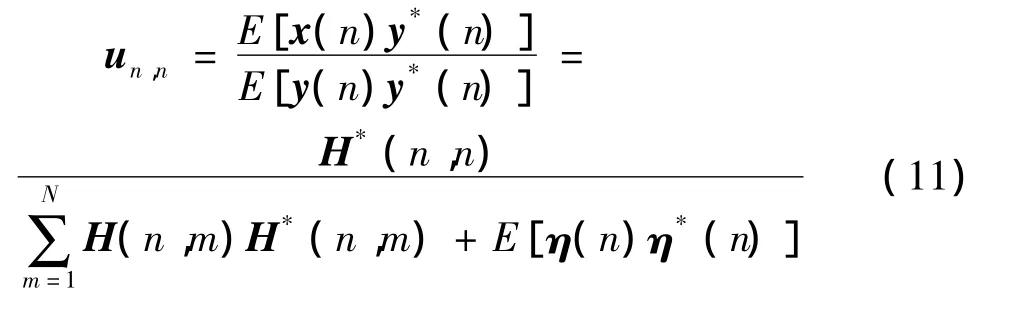
3 仿真分析

系统采用QPSK调制方式，仿真参数为:OFDM系统子载波数为128个，其中数据子载波104个，导频子载波24个，采样点数为128，循环前缀长度为32。Ka频段移动卫星信道模型在不同天气、环境下的参数如表1—表3所示［9-10］。

表1 不同天气下的模型参数Tab.1 Parameters of themodel in differentweather conditions

表2 不同阴影环境下模型的包络参数Tab.2 Envelope parameters of themodel in different shadowing conditions

表3 不同阴影环境下模型的相位参数Tab.3 Phase parameters of themodel in different shadowing conditions

3.1 最优阶次选择

图3给出了当fd=300 kHz时，在不同环境中，目标函数f（p）随系统阶次的变化曲线。

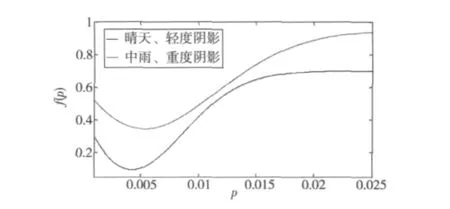
图3 不同FRFT阶次下f（p）的变化曲线Fig.3 Curve of f（p）in different orders of FRFT

在图3的2种环境条件下，f（p）分别在p约为0.004和0.005时取得最小值，并且可以看出二者的ICI存在较大差别。

3.2 Ka频段FRFT-OFDM系统误码率分析

图4、图5分别给出了晴天、轻度阴影与中雨、重度阴影时，不同多普勒频移环境中（fd=100 kHz，300 kHz，500 kHz），在各自对应的最优阶次下，Ka频段FFT-OFDM系统与FRFT-OFDM系统的误码率曲线。

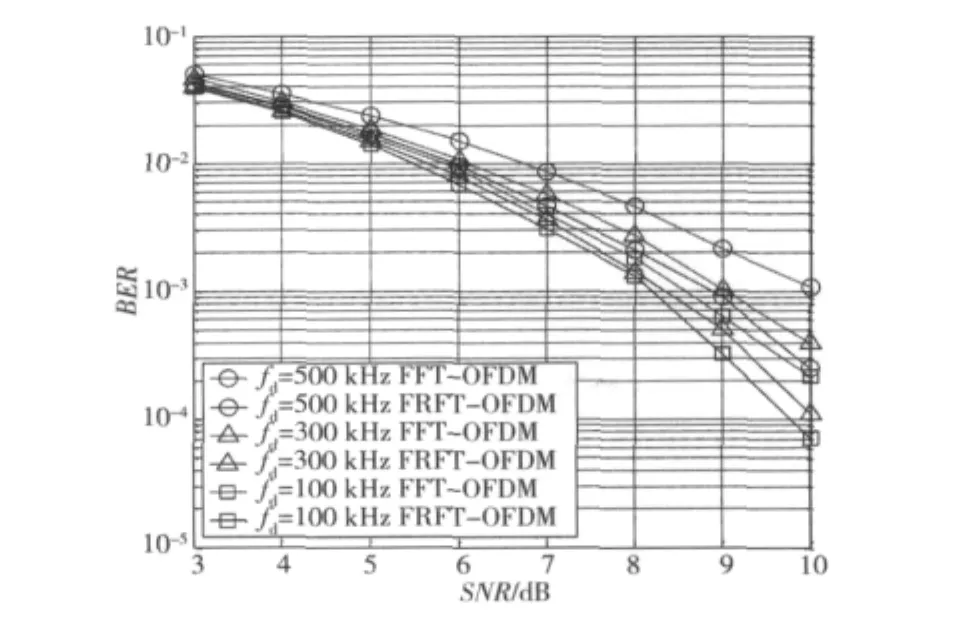
图4 晴天、轻度阴影时，不同多普勒频移下系统性能比较Fig.4 BER performance in different Doppler shifts under clear sky and light shadowing

从图4和图5可以看出，在不同多普勒频移环境下，FRFT-OFDM系统性能较FFT-OFDM系统均有所改善。其中晴天、轻度阴影条件下，在误码率为10－3时，fd=100 kHz，300 kHz，500 kHz 的 FRFTOFDM系统可分别带来约0.4 dB，0.6 dB和1.2 dB的信噪比增益;而中雨、重度阴影条件下，在误码率为10－2时，可分别带来0.6 dB，1 dB和1.6 dB的信噪比增益。由此可见，fd越大，FRFT-OFDM系统的性能改善越明显。

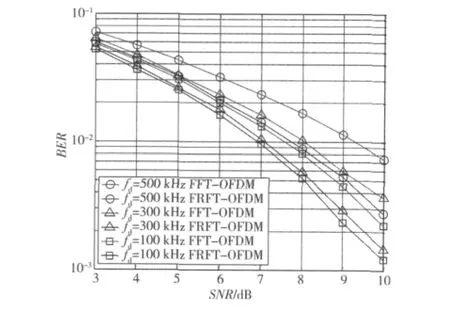
图5 中雨、重度阴影时，不同多普勒频移下系统性能比较Fig.5 BER performance in different Doppler shifts under rain and heavy shadowing

3.3 Ka频段FRFT-OFDM系统均衡仿真

图6、图7给出了当fd=300 kHz时，不同环境条件下，系统在分数阶傅里叶域和频域进行均衡后误码率的比较曲线。

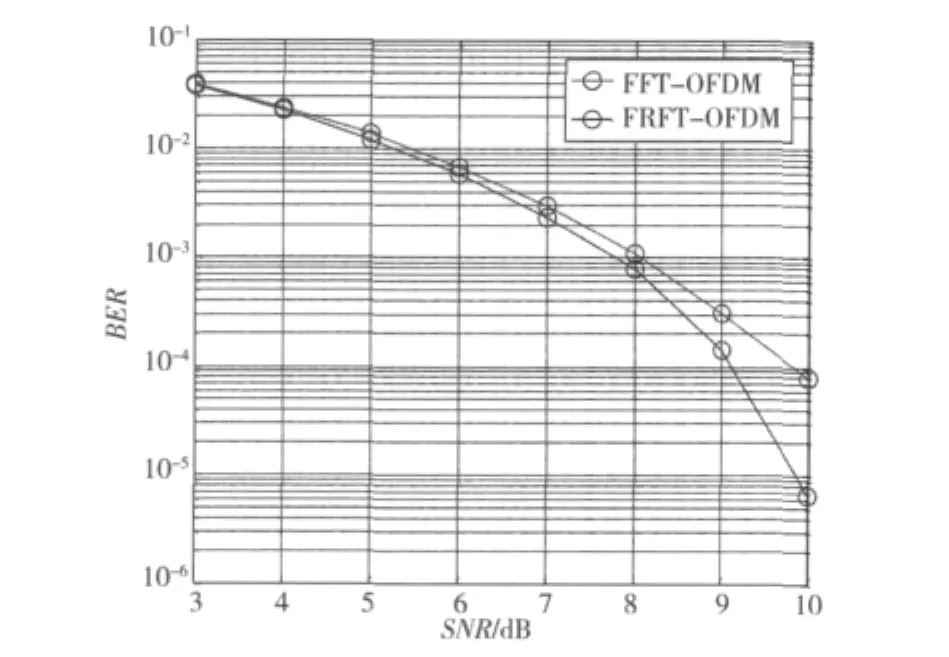
图6 晴天、轻度阴影时系统均衡的性能比较Fig.6 Comparison of equalization performance under clear sky and light shadowing

从图6和图7可以看出，不同环境下，Ka频段OFDM系统在最优阶次分数阶傅里叶域进行均衡得到的误码率性能较频域均衡均有明显提高。晴天、轻度阴影条件下，在误码率为10－4时，FRFT-OFDM系统可带来约0.7 dB的信噪比增益;中雨、重度阴影条件下，在误码率为10－3时，FRFT-OFDM系统可带来约1.1 dB的信噪比增益。

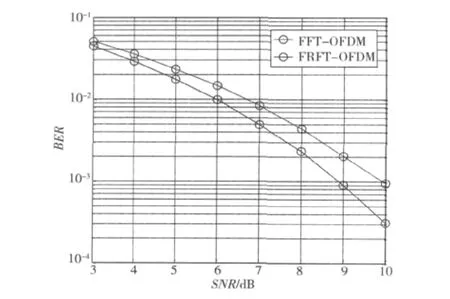
图7 中雨、重度阴影时系统均衡的性能比较Fig.7 Comparison of equalization performance under rain and heavy shadowing

4 结束语

本文在分析Ka频段移动卫星信道特性的基础上，将多普勒频移fd引入信道模型，利用FRFT改进了Ka频段的OFDM系统，就不同环境中的系统最优阶次进行了选择。通过比较分析本系统在不同多普勒频移条件下与传统OFDM系统的误码率性能，得出fd越大，FRFT-OFDM系统性能改善越明显的结论，并在fd=300 kHz时，对Ka频段OFDM系统进行了分数阶傅里叶域和频域均衡的比较。仿真结果显示，本系统在最优阶次分数阶傅里叶域进行均衡后得到的误码率性能较传统OFDM系统在不同的天气、环境条件下均有明显改善，因而有较大的实用参考价值。

［1］MARTONEM.A Multicarrier System Based on the Fractional Fourier Transform for Time Frequency Selective Channels［J］.IEEE Trans on Communications，2001，49（6）:1011-1020.

［2］ 靳晓嘉，陈波，刘鑫，等.一种降低OFDM系统峰均功率比的算法［J］.北京邮电大学学报，2004，27（5）:60-64.

JIN Xiao-jia，CHEN Bo，LIU Xin，et al.A New Algorithm for Reducing the PAPR of OFDM Signals［J］.Journal of Beijing University of Posts and Telecommunications，2004，27（5）:60-64.

［3］ 唐建明，孙小霞，徐位凯.基于编码的OFDM系统性能仿真［J］.重庆邮电大学学报:自然科学版，2009，21（3）:348-352.

TANG Jian-ming，SUN Xiao-xia，XUWei-kai.Performances simulation of coded OFDM systems［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2009，21（3）:348-352.

［4］ 张更新，张杭.卫星移动通信系统［M］.北京:人民邮电出版社，2001:96-97.

ZHANG Geng-xin，ZHANG Hang.Satellite Mobile Communication System［M］.Beijing:People's Post and Telecom Press，2001:96-97.

［5］GLEASON S，HODGART S，SUN Yi-ping.Detection and processing of bistatically reflected GPS signals from low earth orbit for the purpose of ocean remote sensing［J］.IEEE Trans on Geosciences and Remote Sensing，2005，43（6）:1229-1241.

［6］阎啸天，武穆清.辅助定位卫星多普勒频移特性［J］.北京邮电大学学报，2009，32（2）:66-70.

YAN Xiao-tian，WU Mu-qing.On Assisted GPS Doppler Characterization［J］.Journal of Beijing University of Posts and Telecommunications，2009，32（2）:66-70.

［7］王爱华，罗伟雄.Ka频段卫星通信信道建模及系统性能仿真［J］.通信学报，2001，22（9）:61-69.WANG Ai-hua，LUO Wei-xiong.Modeling of Ka-band satellite communication channel and system performance simulation［J］.Journal of China Institute of Communications，2001，22（9）:61-69.

［8］黄和，王东进，刘发林.Ka波段移动卫星信道的综合模型及误码率分析［J］.中国科技大学学报，2005，35（3）:346-353.

HUANG He，WANG Dong-jin，LIU Fa-lin.Modeling of Ka-band Mobile Satellite Channel and Ber Performance Analysis［J］.Journal of University of Science and Technology of China，2005，35（3）:346-353.

［9］ LIWen-zhen，LAW Choi Look，DUBEY V K，et al.Kaband Land Mobile Satellite Channel Model incorporating weather effects［J］.IEEE Communications Letters，2001，5（5）:194-196.

［10］ CHUN Loo，BUTTERWORTH JS.Land mobile satellite channelmeasurement and modeling［J］.Proceedings of the IEEE，1998，86（7）:1442-1463.

［11］陶然，邓兵，王越.分数阶傅里叶变换及其应用［M］.北京:清华大学出版社，2009:2-7.

TAO Ran，DENG Bing，WANG Yue.Fractional Fourier Transform and Its Applicaations［M］.Beijing:Tsinghua University Press，2009:2-7.

［12］陈恩庆，陶然，张卫强，等.一种基于分数阶傅里叶变换的OFDM系统及其均衡算法［J］.电子学报，2007，35（3）:409-414.

CHEN En-qing，TAO Ran，ZHANGWei-qiang，et al.The OFDM System and Equalization Algorithm Based on the Fractional Fourier Transform［J］.Acta Electronica Sinica，2007，35（3）:409-414.