树上n维乘积自映射等度连续的充要条件*

杨 柳

(重庆师范大学数学学院，重庆 401331)

在动力系统的研究中，不变点集性质的研究是十分重要的工作，对于区间上的连续自映射所产生的动力系统来说，已经有了较多而且比较深刻的结果.此处主要研究树上n维乘积自映射所具有的一些性质.

系统的等度连续性是系统稳定性的一种刻划，对于区间上连续自映射和圆周自映射的周期点集上的等度连续性，文献［1］-［3］分别进行了讨论，文献［4］给出了树上连续自映射在周期点集上具有等度连续性的几个充要条件，此处在他们的基础上给出了树上n维乘积自映射在周期点集上具有等度连续性的3个充要条件.

下面给出一些基本概念和记号.

记T为树，即不含有圈的一维紧致连通的分支流形，f∈C°(X，X)表示紧致度量空间(X，d)上的连续自映射，T，T1，T2，…，Tn均表示树，设(X1，d1)，(X2，d2)，…，(Xn，dn)是紧致度量空间，

定义1［1］设X为一拓扑空间，f∈C°(X，X)，用f°表示恒等映射，对任意自然数n，归纳地定义f1=f，f2=f°f，…，fn=f°fn-1.

定义2［1］设x∈X，若存在自然数n，使得fn(x)=x，则称x为f的周期点，f的周期点集记作P(f).

定义3［2］设x∈X，若对x的任何邻域V(x)，存在自然数n，使得fn(x)∈V(x)，则称x为f的回归点，记f的回归点集为R(f).

定义4［2］设f∈C°(X，X)，称x是f的异状点，若存在p∈P(f)，满足

①x≠p;②x∈Wu(p，fn)，这里Wu(p，f)表示p的非稳定流形，n是p的周期;③存在m∈N，fmn(x)=p.

定义5［5］设f∈C°(X，X)，若∀ε ＞0，∀p∈P(f)，存在p的邻域V(p)，使得直径 diam(fm(V(p)∩P(f)))＜ε，∀m≥0，则称等度连续.

定义6［5］X×X×…×X的度量 ρ为

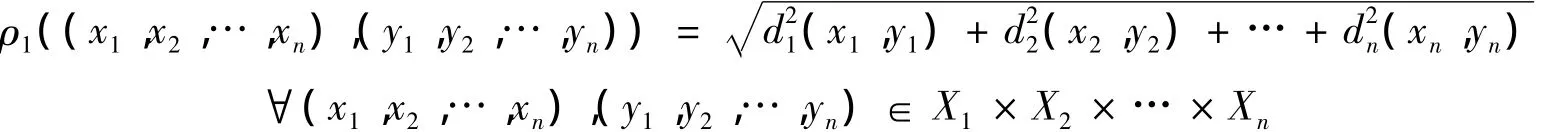
1 若干引理

引理 1 若f∈C°(T，T)，则fP(f)具有等度连续性等价于h(f)=0.

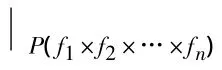
引理3 若f∈C°(X，X)，p∈F(fn)，n＞0，则Wu(p，fn)=Wu(p，fkn)，∀k＞0.

引理 4 若fi∈C°(X，X)(i=1，2，…，n)，则

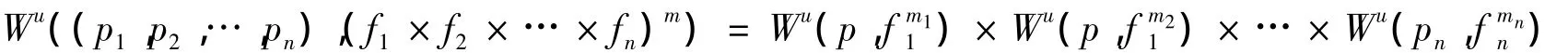
其中m=［m1，m2，…，mn］为m1，m2，…，mn的最小公倍数，m1，m2，…，mn分别是p1，p2，…，pn的周期.

证明 ∀z=(x1，x2，…，xn)∈WU((p1，p2，…，pn)，(f1×f2×… ×fn)n)，设V(pi)分别是pi的任意一个邻域，则V(p1)×V(p2)×… ×V(pn)是(p1，p2，…，pn)的一个邻域.由于z∈WU(p1，p2，…，pn)，存在k＞0，使得z=(x1，x2，…，xn)∈(f1×f2x× … ×fn)kn(V(P1)×V(P2)× … ×V(Pn))，从而xi∈(V(pi))，即xi∈WU(pi).故(x1，x2，…，xn)∈WU(p1)×WU(p2)×… ×WU(pn)，即

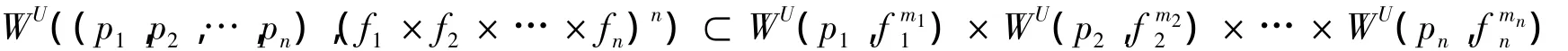
反之，∀xi∈WU(pi)(i=1，2，…，n)，令z=(x1，x2，…，xn)，下证z∈WU((p1，p2，…，pn)，(f1×f2× … ×fn)n)，因xi∈WU(pi)(i=1，2，…，n)，由引理 4，存在→pi及mli，使()→xi，li→ + ∞，i=1，2，…，n，若=对于无穷多个li成立，则(f1×f2× … ×fn)n，…)→(x1，x2，…，xn)，且(，…)→(p1，p2，…，pn)，不妨设＞，对于无穷多个k成立.

令ti=)，则(f1×f2×… ×(t1，t2，…，tn)→(x1，x2，…，xn)，总之z=(x1，x2，…，xn)∈WU((p1，p2，…，pn)，(f1×f2×… ×fn)n)，即证.

引理5 若f∈C°(X，X)，则f有异状点等价于存在n＞0，p∈F(fn)，及z∈WU(p，fn)，z≠p，fn(z)=p.

引理6 若f∈C°(T，T)，则f有异状点等价于h(f)＞0.

引理 7 设fi∈C°(Xi，Xi)，i=1，2，…，n，则

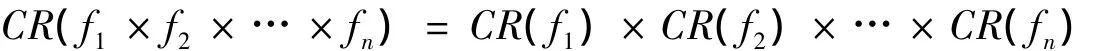
证明 ∀z=(x1，x2，…，xn)∈CR(f1×f2× … ×fn)，∀ε ＞0，有z到z的 ε -链，设为{z0=z，z1，…，zn=z0}，令zi=，…，)，i=1，2，…，n，由于 ρ(f1×f2× … ×fn(zi-1)，zi)＜ ε，i=1，2，…，n，即ρ((f1()，f2()，…，fn()，(，…，))＜ε，从而di(fi)，xii)＜ε，故xi∈CR(fi)，即CR(f1×f2×… ×fn)⊂CR(f1)×CR(f2)×… ×CR(fn).反之，∀(x1，x2，…，xn)∈CR(f1)×CR(f2)×… ×CR(fn)，即xi∈CR(fi)，则∀ε ＞0，存在从xi到xi的 ε - 链，分别设为{=xi，，…=}.从而可以构造n条长度为m1m2…mk+1的ε-链如下:

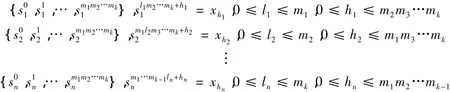
令zi=(，…)，0≤i≤m1m2…mk，则

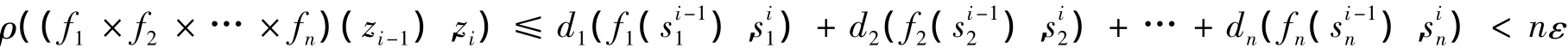
由 ε的任意性，n的有限性，(x1，x2，…，xn)∈CR(f1×f2×… ×fn)，从而CR(f1)×CR(f2)×… ×CR(fn)，即证.

引理 8 设fi∈C(Xi，Xi)，i=1，2，…，n，则

这里Asp(f)表示f的渐进周期点.

证明 ∀(x1，x2，…，xn)∈Asp(f1×f2×… ×fn)，存在(p1，p2，…，pn)∈P(f1×f2× … ×fn)，使得 ρ((f1×f2×… ×fn)n(x1，x2，…，xn)，(f1×f2× … ×fn)n(p1，p2，…，pn))→0，n→ + ∞，从而di((xi)，(pi))→0，n→ +∞.由于P(f1×f2× … ×fn)=P(f1)×P(f2)× … ×P(fn)，故pi∈P(fi)，所以xi∈Asp(fi)，即(x1，x2，…，xn)∈Asp(f1)×Asp(f2)×…×Asp(fn)，故 Asp(f1×f2×…×fn)⊂Asp(f1)×Asp(f2)×… ×Asp(fn).反之，若xi∈Asp(fi)，存在pi∈P(fi)，有di((xi)，(pi))→0，n→ + ∞，从而 ρ((f1×f2× … ×fn)n(x1，x2，…，xn)，(f1×f2×… ×fn)n(p1，p2，…，pn))→0，n→ +∞，又P(f1×f2×… ×fn)=P(f1)×P(f2)×… ×P(fn)，故(p1，p2，…，pn)∈P(f1×f2×… ×fn)，所以(x1，x2，…，xn)∈Asp(f1×f2×… ×fn)即 Asp(f1×f2× … ×fn)⇔Asp(f1)×Asp(f2)×…×Asp(fn)，即证.

2 主要结果

定理1 设fi∈C°(Ti，Ti)，i=1，2，…，n，则(f1×f2×… ×fn)具有等度连续性等价于h(f1×f2×…×fn)=0.

证明 “⇒”因为(f1×f2×…×fn)具有等度连续性，由引理 2，也具有等度连续性，再由引理1，h(fi)=0，i=1，2，…，n，故h(f1×f2× … ×fn)=h(f1)+h(f2)+… +h(fn)=0.

“⇐”由h(f1×f2× … ×fn)=0，则h(fi)=0，i=1，2，…，n，由引理1，分别具有等度连续性，再由引理2得(f1×f2×…×fn)具有等度连续性.

定理2 设fi∈C°(Ti，Ti)，i=1，2，…，n，则(f1×f2× … ×fn)具有等度连续性等价于f1×f2×…×fn没有异状点.

证明 “⇒”由(f1×f2×… ×fn)具有等度连续性，再由定理 1，h(f1×f2× … ×fn)=0，故h(fi)=0，i=1，2，…，n，最后由引理6，fi都没有异状点.

现假设f1×f2×… ×fn有异状点z=(x1，x2，…，xn)，则存在p=(p1，p2，…，pn)是f1×f2× … ×fn的周期点，满足(x1，x2，…，xn)≠(p1，p2，…，pn).

(x1，x2，…，xn)∈WU((p1，p2，…，pn)，(f1×f2× … ×fn)n)，n是p的周期，且存在m＞0，(x1，x2，…，xn)=(f1×f2×… ×fn)kn(p1，p2，…，pn)，设pi的周期为mi，i=1，2，…，n，则mi都能整除n，由引理 4

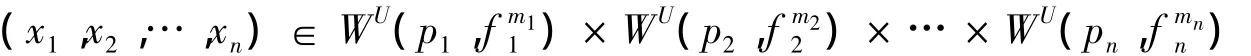
故xi∈WU(pi，)，并且由(x1，x2，…，xn)=(f1×f2× … ×fn)kn(p1，p2，…，pn)，则xi=(pi)=(pi)，其中kini=n，又由已知(x1，x2，…，xn)≠(p1，p2，…，pn).则x1≠p1或x2≠p2或xn≠pn，不妨设x1≠p1，则x1是f1的异状点，与f1没有异状点矛盾，故f1×f2×…×fn没有异状点.

“⇐”假设(f1×f2×…×fn)不是等度连续的，由定理1，h(f1×f2×… ×fn)＞0，故h(f1)＞0或h(f2)＞0或h(fn)＞0，不妨设h(f1)＞0，由引理6，f1有异状点，由引理5，存在n1＞0，p1∈F()及z1∈WU(p1，)，z1≠p1(z1)=p1.设pi是fi的周期点(i=2，3，…，n)，且周期为mi，记z=(z1，p2，…，pn)，由z1≠p1，故z=(z1，p2，…，pn)≠(p1，p2，…，pn)=p.设n=［m1，m2，…，mn］，则(f1×f2× … ×fn)n(z)=(z1)(p2)，…(pn))=(p1，p2，…，pn)=p，且n是p的周期.

下证z∈WU((p1，p2，…，pn)，(f1×f2×… ×fn)n):

设V(p)是p的任一个邻域，则存在V(pi)是pi的邻域，满足V(p1)×V(p2)×…×V(pn)⊂V(p)，因z1∈WU(p1)，由引理 3，z1∈WU(p1)，从而存在k＞0，z∈(V(p1))，又pi是fi的周期为ni的周期点，i=2，3，…，n，故pi∈n(V(pi))，从而(z1，p2，…，pn)∈(f1×f2× … ×fn)kn(V(p1)×V(p2)× … ×V(pn))⊂fkn(V(p1))，即 z=(z1，p2，…，pn)∈WU((p1，p2，…，pn)，(f1×f2× … × fn)n)，由引理 5，f1× f2× … × fn有异状点，与已知矛盾.

证明 “⇒”P(F)对F 具有等度连续性，由定理1，h(F)=0，故 h(f)=0，∀z=(x1，x2，…，xn)∈CR(F)P(F)，由引理8及 P(f1×f2×… ×fn)=P(f1)×P(f2)×… ×P(fn)，有 xi∈CR(f)P(f)(i=1，2，…，n)，由引理 12，xi∉Asp(f)，由引理 9，(x1，x2，…，xn)∉Asp(F).

“⇐”∀xi∈CR(f)P(f)(i=1，2，…，n)，由引理8及 P(f1×f2×… ×fn)=P(f1)×P(f2)×… ×P(fn)，则(x1，x2，…，xn)∈CR(F)P(F)，由已知，(x1，x2，…，xn)∉Asp(F)，由引理 9，xi∉Asp(f)，不妨设 x2∉Asp(f)，由引理12，h(f)=0，从而h(F)=0，故P(F)对F具有等度连续性.

［1］熊金城.线段映射的动力体系:非游荡集，拓扑熵以及混乱［J］.数学进展，1988，17(1):1-11

［2］周作领.线段自映射的周期点集［J］.数学学报，1986，29(2):272-275

［3］杨润生.圆周自映射的周期点集的局部度量稳定性［J］.南京师大学报:自然科学版，1998(4):14-17

［4］严珍珍，杨润生.树上乘积自映射周期点集的局部度量稳定性［J］.系统科学与数学，2004，24(1):35-40

［5］严珍珍.周期点集的局部度量稳定性［J］.南京师大学报:自然科学版，2001(2):7-10

［6］牛应轩.树映射有异状点的一个充要条件［J］.数学研究，1999(3):272-276

［7］孙太祥.树映射的动力系统的研究［D］.中山:中山大学，2001