F幂群的直积*

杨培亮，王少敏

(大理学院数学与计算机学院，云南大理 671003)

模糊数学的发展突出了极值映射的重要性，各种数学结构需要由论域向其幂集上提升，如序结构的提升、可测结构的提升、拓扑结构的提升等等［1］.于是开始了幂群、幂环、超拓扑群、粗糙幂半群的研究［2-7］.模糊数学的发展要求各种数学结构不但要由论域向其幂集上提升，而且还要求向模糊幂集上提升.于是开始了Fuzzy幂群、Fuzzy幂环的研究［7-10］.文献［1］首先提出Fuzzy幂群的概念，讨论了Fuzzy幂群的结构及其同态问题.在文献［1］的基础上进一步研究了F幂群，讨论了F幂群的直积.

1 预备知识

全文始终假定X是一个群，X上的全体Fuzzy子集记为F(X).

由多元扩展原理，群X中的运算可以扩展到F(X)中:∀A，B∈F(X)，定义

其中，Aλ是A的λ截集，定义

不妨约定，ØA=AØ=Ø.

几个结论［1］:

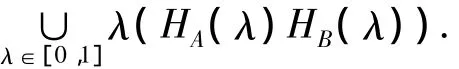
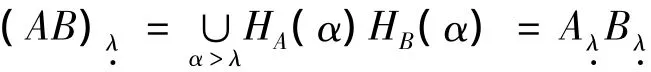
(4)(AB)C=A(BC)，A，B，C∈F(X).

定义1［1］设X是群，R⊆F(X)，若R对运算(1)构成群，则称R为X上的一个F幂群，其单位元用E，A∈R，A的逆元用A-1表式.

约定Ø是F幂群，显然幂群也是F幂群.

2 F幂群的直积

先讨论两个F幂群的直积，再推广到有限个F幂群的直积.

定理1 设X1，X2是群，X=X1×X2是X1与X2的直积群，设R1与R2分别是群X1与X2上的F幂群，作∈R1，A2∈R2}在R上定义乘法:

则R是X上的F幂群.

证明 1)∀(A1，A2)，(B1，B2)，(C1，C2)∈R，有

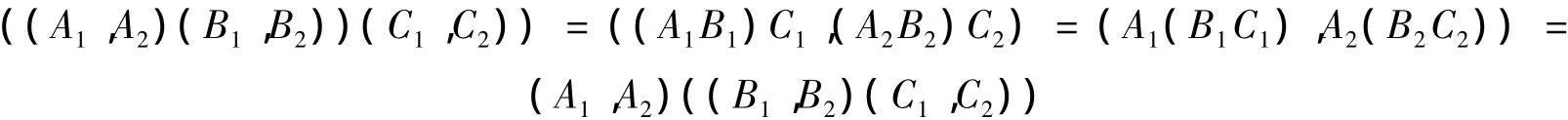
2)(A1，A2)(E1，E2)=(A1E1，A2E2)=(A1，A2)=(E1A1，E2A2)=(E1，E2)(A1，A2)，因而(E1，E2)是单位元.

3)(A1，A2))=(A1，A2)=(E1，E2)=(A1A2)=()(A1，A2)，因此()是(A1，A2)的逆元.

所以R是X上的F幂群.

定义2 称定理1中的F幂群R为F幂群R1与R2的直积群.

定理2 设X1，X2是群，X=X1×X2是X1与X2的直积群，R=R1×R2是X1×X2上的F幂群，投影映射为:

则R1，R2分别为X1，X2上的F幂群.

证明 ∀A1，B1，C1∈R1，A2，B2，C2∈R2，则(A1，A2)，(B1，B2)，(C1，C2)∈(R1× R2)

1)(A1，A2)(B1，B2)=(A1B1，A2B2)，A1B1∈R1，A2B2∈R2.故封闭.

2)((A1，A2)(B1，B2))(C1，C2)=((A1B1)C1，(A2B2)C2)=(A1，A2)((B1，B2)(C1，C2))=(A1(B1C1)，A2(B2C2)).故结合律成立.

3)设(E1，E2)是 R 的单位元，(E1A1，E2A2)=(E1，E2)(A1，A2)=(A1，A2)=(A1，A2)(E1，E2)=(A1E1，A2E2).故E1是R1的单位元，E2是R2的单位元.

4)设(D1，D2)是(A1，A2)的逆元，(E1，E2)=(D1，D2)(A1，A2)=(D1A1，D2A2)=(A1，A2)(D1，D2)=(A1D1，A2D2).故D1是A1的逆元，D2是A2的逆元.

综上所得R1，R2分别为X1，X2上的F幂群.

定理3 群X1和X2上的F幂群与X1×X2上的F幂群可以相互唯一决定.

证明 由定理1和定理2可得.

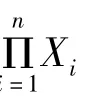
定理4 设X1，X2，…，Xn是群，X= 是它的直积群，设Ri是Xi上的F幂群，则R=×…×Rn)，R上定义乘法:则R是X上的F幂群.

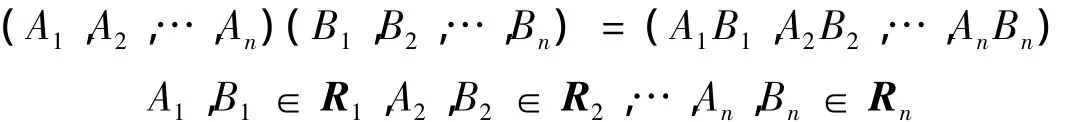
证明与定理1的证明类似.

定义3 称定理4中的F幂群R为有限个F幂群R1，R2，…，Rn的直积群.

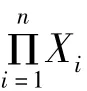
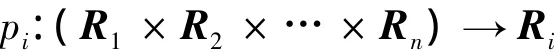
证明与定理2的证明类似.

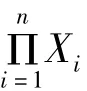
证明 由定理5和定理6可得.

［1］罗承忠，米洪海.Fuzzy幂群［J］.模糊系统与数学，1994，8(1):1-9

［2］丰建文，方成鸿，汤文菊.幂环的结构与分类［J］.模糊系统与数学，2008，12(6):47-52

［3］杨培亮，刘文军.超拓扑群的连通性［J］.科学技术与工程，2011，7(19):4553-4555

［4］张振良，张金玲，肖旗梅.模糊代数与粗超代数［M］.武汉:武汉大学出版社，2007

［5］王开宝，祝令江，姚炳学，等.幂群的结构与构造［J］.科学技术与工程，2008，6(12):3067-3070

［6］王开宝，祝令江，王丽，等.幂群结构的推广［J］.聊城大学学报，2008，6(2):55-56

［7］杨培亮，王少敏.粗糙幂半群［J］.重庆工商大学学报:自然科学版，2011，11(6):577-579

［8］杨培亮，张振良.F幂群的性质与结构［J］.纯粹数学与应用数学，2002，9(3):282-287

［9］杨培亮，张振良.F幂群的分类［J］.模糊系统与数学，2003，3(1):53-58

［10］张晓丽，张振良.模糊幂环［J］.模糊系统与数学，2004，3(1):31-35