基于K-均值聚类的朴素贝叶斯网络分类模型

刘亚辉，王 越，谭暑秋

(重庆理工大学计算机科学与工程学院，重庆 400054)

朴素贝叶斯网分类器(Naïve Bayesian classifier，NB)［1］是目前被公认的一种简单而有效的概率分类的方法，它同时也是贝叶斯网分类器的一种。从某种意义上来说其预测性能可与神经网络、决策树等算法相媲美，因此在某些领域中表现出了它性能的优异性［2］。许多工作研究者从不同的方向思考，并从NB方法中的“独立性假设”出发，为了提高分类器的性能从而构造出了不同的改进模型［3-5］。由于朴素贝叶斯网络的分类模型以各个非类属性变量相对于类属性变量相对独立为前提的，也就是各个非类属性变量独立地作用于类属性变量。此前提条件在一定程度上限制了朴素贝叶斯网络分类模型的适用范围，虽然降低了贝叶斯网络的构建复杂性，但是当处理的数据维数较多，且数据量较大时，朴素贝叶斯网络分类的效率则是偏低的，其准确率有待提高。在朴素贝叶斯网络的基础上结合主元分析法与K-均值聚类算法构造出了一个改进的朴素贝叶斯网络的分类模型。由于主元分析法是解决多维数据行之有效的方法，而K-均值聚类算法能够使簇内具有较高的相似度，而簇间的相似度较低，这将有便于从多维属性中有效地进行降维处理。

1 相关概念

概念1(相对融合点) 在一个数据集D=(x1，x2，…，xn)中，设存在一个值x'能够代表数据中的特点并与数据集具有很好的拟合性，则x'称为相对融合点。

概念2(K-均值聚类)K-means算法以K为参数，把N个对象分为K个簇，以使簇内的相似度较高，而簇间的相似度较低。根据一个簇中的平均值(视为簇重心)来进行相似度的计算。K-means算法的处理过程如下:(1)随机选择K个对象，每一个对象初始代表一个簇的中心或平均值。计算剩余的每个对象与各个簇中心的距离，再将剩余的对象赋给最近的簇。(2)不断重复地计算每个簇的平均值，直至准则函数收敛到期望值［6］。

概念3(主元分析) 主元分析(PCA)是在有一定相关性的m个样本值与n个参数所构成的数据阵列的基础上，通过建立较小数目的综合变量，使其更集中的反映原有数据阵列中包含的信息的方法［7］。

2 算法描述

设存在一张数据表，有m个对象记为X1，X2，…，Xm，有n个属性记为a1，a2，…，an。其中每个对象Xi=(xi1，xi2，…，xin)，i=1，…，m，且xij(j=1，…，n)代表对象Xi的aj属性。同样aj=(x1j，x2j，…，xmj)，j=1，…，n。因此这张表可以用下面的矩阵来表示:

在一个历史数据集中总是会出现一些数据保存不完善的情况，而且丢失数据不只一个。为了使问题更容易地呈现，只讨论一个数据丢失数据的情况。当然此过程也可以被用到多个数据的丢失。改进的朴素贝叶斯算法的步骤如下:

假设Xj是缺损比较严重的数据列，属性Xj的值需要修补完整。在此假设数据的属性列比较多，算法的基本步骤如下:

第1步:利用PCA算法降维。

(1)删除矩阵B的第j列，得到如下矩阵D:

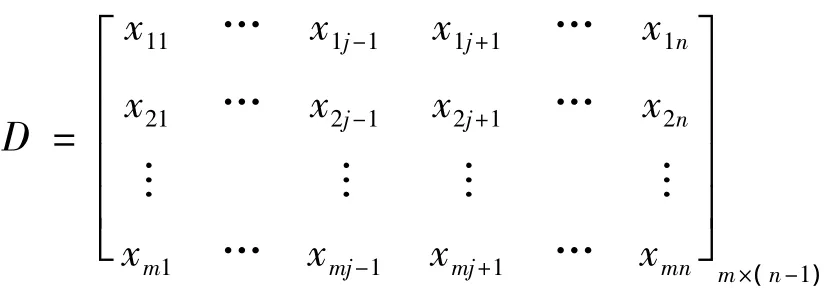
(2)对样本数据进行标准化处理。

(3)计算相关矩阵。对给定的m个样本，计算指标变量的相关系数矩阵:

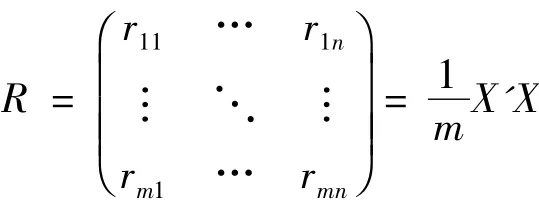
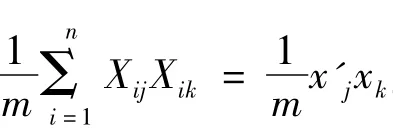
(4)求特征值和特征向量。求解特征方程:|R-λf|=0。通过此方程，可得到k个特征值(i=1～n)与对应于每一个特征值的特征向量Qi=(ai1，ai2，…，aip)，其中i=1～k。

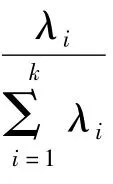
(6)设通过PCA

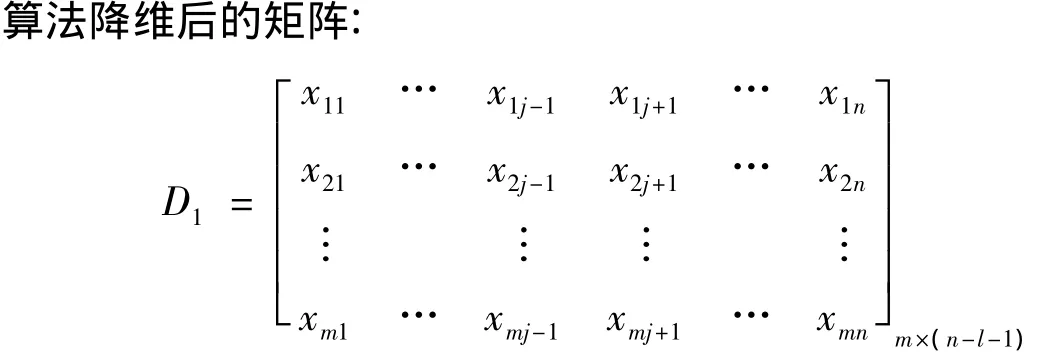
第2步:求降维后各列属性值的相对融合点。

设列属性yi={x1j，x2j，…，xmj}且j=1，…，n-l-1，则D1={y1，y2，…，yn}。设列属性yi中任何两个值之间的距离为d(xhi，xki)。

(1)求数值点的密度。确定一个正数d0，以每个数据为中心d0为半径作n维空间的超球，令d(xhi，xki)为xhi到xki的距离，其中d(xhi，xki)=(h，k=1，2，…，m;j≠k)，若满足d(xhi，xki)≤d0则认为xki落在以xhi为圆心的超球内，落在超球内的点的总数为xhi的密度phi。不难发现，phi越大，则以它为相对融合点的资格就越大。

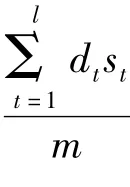
第3步:用K-均值算法对数据进行聚类。

(1)初始时设前k个数作为簇的均值，并建立k个集合。依次分别把D1中的前k个数据依次放入到S1，S2，…，Sk(k≤n，k≠j)中，即S1={y'1}，S2={y'2}，…，Sk={y'k};

(2)依次从D1中取数据对象y'k+1，…，y'n，利用欧几里德公式计算每个数据对象与每个簇均值的距离dqh=|y'q-y'h|(1≤q≤k，k+1≤h≤n)，dmin=min{dqh};

(4)若这k个集合里面的元素不再发生变化时，聚类结束。

第4步:形成贝叶斯网络模型。

对聚类产生的各个元组中用鉴别信息来计算各个属性之间的相互关系。最后再增加类到各个元组之间的有向边。

图1 聚类后局部贝叶斯网络结构示意图

为了便于理解，设类属性为C，各个非类属性为X={X1，X2…Xn}。设各个元组产生的聚类结果S1={X1，X3，X4，X9}，S2={X5，X13，X23}，…，Sk={X33，X38，X39，X41}。则经过第一步处理之后如图 1 所示。则最后形成的贝叶斯网络如2所示。

第5步:对缺损的值分类分析后进行修补。

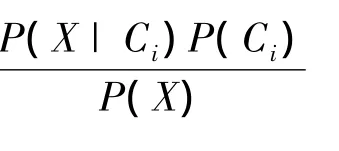
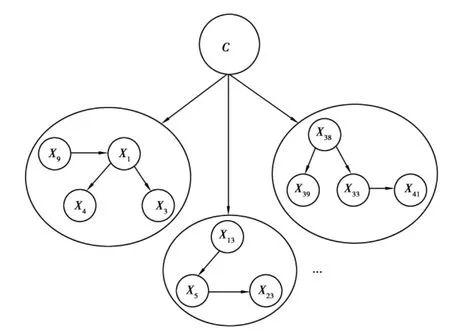
图2 形成的贝叶斯网络结构示意图

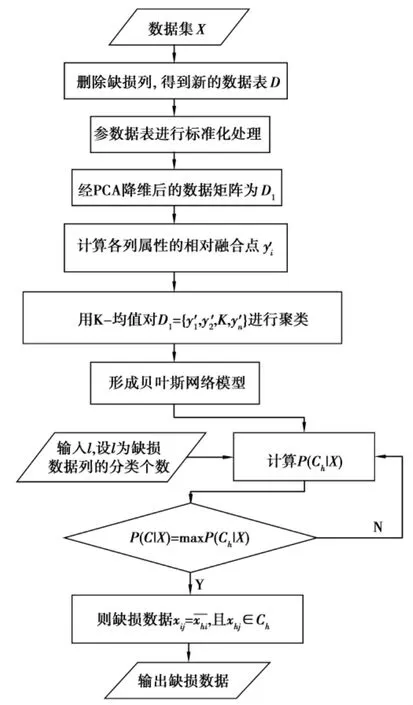
图3 改进的朴素贝叶斯网络算法流程示意图

3 算法性能分析

分类算法模型是以在朴素贝叶斯网络的基础上提出来的，与之不同之处在于算法摒弃了非类属性变量相对于类属性变量是相对独立的前提条件。在改进的算法中，由于处理的数据非常的庞大，故在算法开始就借用了主成分分析法在对数据信息量保存的同时来进行降维操作，这样对算法着重于分类模型的研究有很大的帮助。在改进的算法中，给出了相对融合点这个概念，并给出了获取相对融合点的算法。最后算法利用K-均值来研究各列属性之间存在的隐含的依赖关系，有利于将列属性值进行融合，这样就简化了下一步的K-均值聚类算法在数据中的处于算法对缺损值的分类。算法相当于是扩大了朴素贝叶斯网络应用的领域。当对数据量很大，且各维属性之间又存在着隐含关系时，朴素贝叶斯网络很难达到理想的效果，而改进的算法将是处理这些问题行之有效的办法。

4 实验与分析

实验采用“某工厂3月份高炉数据”样本数据表作为数据集，共有200条数据记录，11个属性:硅Si，锰Mn，磷 P，硫 S，钛Ti，铬Cr，镍 Ni，铁Fe，锌Zn，铜Cu，镁Mg;其中有几个缺失的数据，缺失数据会对分析结果造成一定的影响，减小结果的准确度，必须使用合适的方法对数据进行修补。该数据表的部分数据情况如下表1所示。

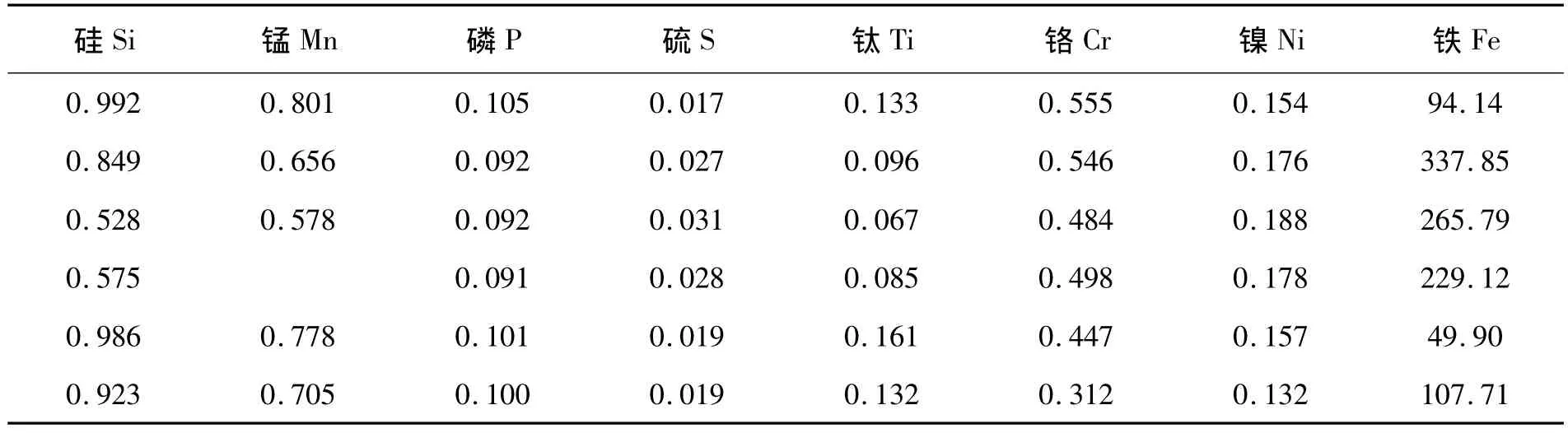
表1 某工厂3月份高炉数据数据表

下面以缺失的第5条数据的“锰Mn”属性值为例，通过实际的实验来说明如何修补该缺失的值。第一步首先删除该缺失值所在的属性列“锰Mn”，对数据表进行标准化处理，那么该数据表变为一个200行10列的数据表，用矩阵表示如下:

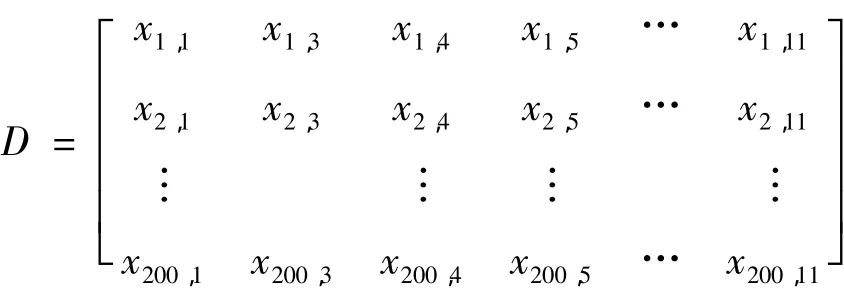
然后对该数据表进行标准化处理，再通过PCA算法作用后，数据表由10维降到了8维，去掉了“钛Ti”，“铜Cu”。降维后的数据表用矩阵D1表示如下:

求降维后各列属性值的相对融合点，并利用相对融合点结合K-均值算法对数据进行聚类，聚类结果得到如下属性分组:S1={铁 Fe}，S2={硅 Si，锌 Zn，镁 Mg}，S3={磷 P，硫 S}，S4={铬 Cr，镍 Ni}。

对删除的属性列“锰Mn”用数学家史特吉斯(Sturges)提出的公式:k=1+3.32logn来对该列数据进行分组，其中n为数据集中数据的个数;则属性值xi如果在［min+l*((max-min)/k)，min+(l+1)*((max-min)/k)］区间内，则变换后的值为l。其中l=0，1，…，k，min是属性列中的最小值，而max是属性列中的最大值，这里每一个分组被认为一个类，有18个分类，即:C1，C2，…，C18。

最后对缺失的x5，2进行修补，具体如下:

5 结束语

针对朴素贝叶斯网络分类模型在处理高维大数据量时的效率偏低和准确率有待提高的问题，在朴素贝叶斯网络的基础上结合主元分析法与K-均值聚类算法构造出了一个改进的朴素贝叶斯网络的分类模型。该模型摒弃了非类属性变量相对于类属性变量是相对独立的前提条件，算法在一开始就用主元分析法在对数据集的信息量尽量保存的同时进行了降维操作，使得算法可以着重于进行分类问题。算法还提出了一个“相对融合点”的概念，并给出了相对融合点的获取方法，有效地提高了算法的性能。最后将改进的算法应用到质量管理中进行了实验，用算法产生的分类结果对数据集中产生的一些缺失数据进行修补，取得了较为理想的结果。

［1］PELIKAN M，GOLDBERG D，SASTRY K.Bayesian optimization algorithm，decision graphs，and Ocam’s razor［R］.Proceedings of the Genetic and Evolutionary Computation Conference(GECCO-2001)，PP.519-526.Also IlliGAL Report No.2000020(2001)

［2］FRIEDMAN N，GEIGER D，GOLDSZMIDT M.Bayesian Network Classifiers［J］.Machine Learning，1997，29:103-163

［3］PELIKAN M，SASTRY K，GOLDBERG D.Scalability of the Bayesian optimization algorithm［J］.International Journal of Approximate Reasoning，2002，31(3):221-258

［4］KAI M，ZHENG Z.A Study of AdaBoost with Naïve Bayesian Classifier:Weakness and Improvement［J］.Computational Intelligence，2003(19):186-200

［5］DING Z，PENG Y，PAN R.BayesOWL:Uncertainty Modeling in Semantic Web Ontologies［J］.In Soft Computing in Ontologies and Semantic Web，Springer-Verlag，December 2005

［6］HAN J，KAMBER M.Data Mining:Concepts and Techniques［M］.Academic Press，2001

［7］王洪春，彭宏.一种基于主成分分析的异常点挖掘方法［J］.计算机科学:2007，10(34):192-194