一类具有分布时滞Liénard方程反周期解的存在性和唯一性*

田龙伟，王良龙，张洪彦

(安徽大学数学科学学院，合肥 230039)

在过去十几年中，人们对Liénard方程的周期解和概周期的存在性和唯一性进行了深入的研究［1-5］.随着科学的发展和应用，对反周期解性质的研究逐渐引起人们的关注［6-12］.在文献［7］中，作者利用 Leray-Schauder度理论研究了一类Liénard 方程x″+f(t，x'(t))+g(t，x(t-τ(t)))=P(t)的反周期解的存在性和唯一性.在此基础上利用Leray-Schauder度理论讨论具有分布时滞的Liénard方程:

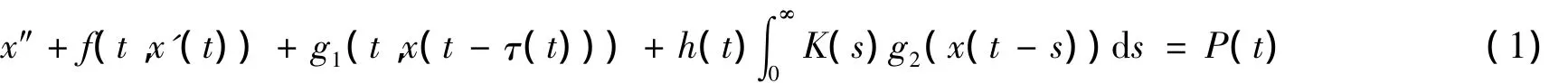
的反周期解的存在性和唯一性，推广了文献［7］中的结果.

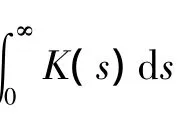
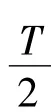
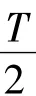
1 准备知识

引理1［13］设Ω是线性赋范空间X中的有界开集，是上的全连续场，如果 deg{，Ω，p}≠0，p∈Xf(∂Ω)，则方程(x)=p在Ω内至少存在一个解.

引理 2［14］设 x∈C2(R，R)，且∀t∈R，x(t+T)=x(t)x(t)dt=0，则

引理3 若方程(1)满足(H2)且满足下列条件之一:

(H3) 存在常数L3，使得

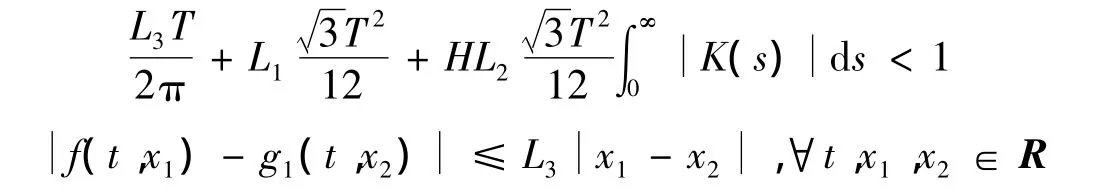
(H4) 存在常数m，使得

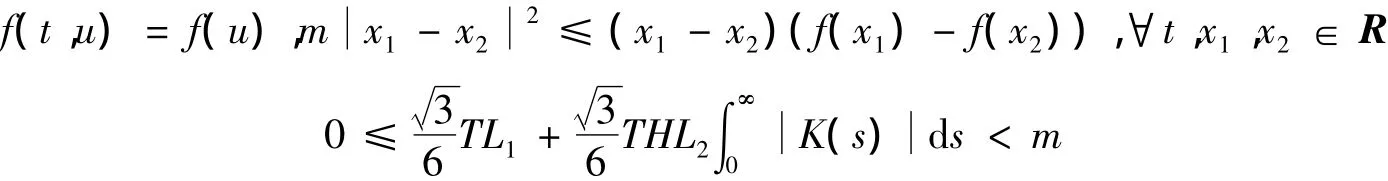
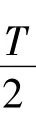
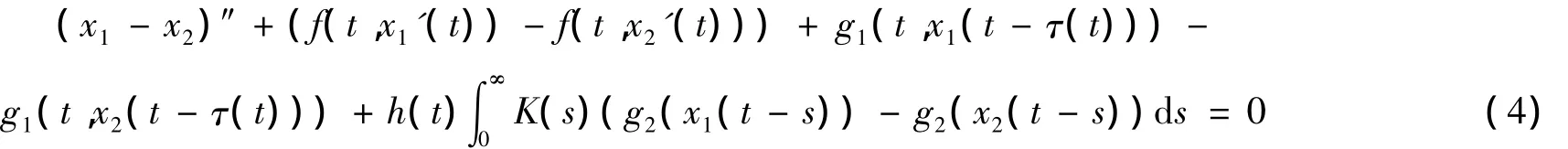
设z(t)=x1(t)-x2(t)，从式(4)知道，

因为z(t)=x1(t)-x2(t)是定义在R上的反周期函数，则

由引理3，有

假设(H3)或(H4)成立，有下列两种情况:

情况1 如果(H3)成立，对方程(5)两边乘以-z(t)且从0到T积分，有

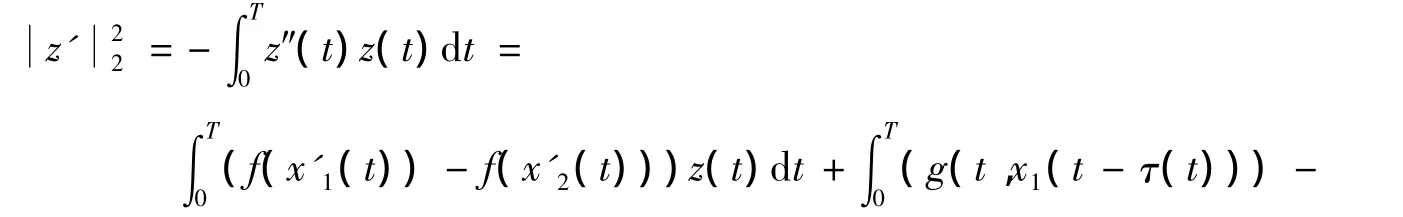
由式(2)(7)及Schwarz不等式，有

因为z(t)，z'(t)都是反周期连续函数，由条件(H3)和式(8)，得z(t)≡z'(t)≡0，∀t∈R.因此x1(t)≡x2(t)，∀t∈R.从而方程(1)至多有一个反周期解.

情况2 如果(H4)成立，对方程(5)两边乘以z'(t)且从0到T积分，有

由式(3)(9)和(H4)，得到 z(t)≡z'(t)≡0，∀t∈R.因此 x1(t)≡x2(t)，∀t∈R.从而方程(1)至多有一个反周期解.

2 主要结论及证明

定理1 设(H1)成立，如果(H3)和(H4)其中之一成立，则方程(1)有唯一的反周期解.

证明 构造方程(1)的辅助方程

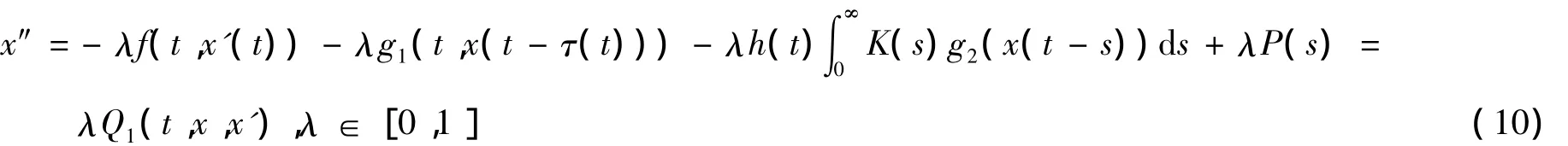
由引理3知，方程(1)至多有一个反周期解，因此要证明定理1，只要证明方程(1)至少有一个反周期解.下面

利用引理1来证明方程(1)至少有一个反周期解.

首先设x∈是辅助方程(10)的反周期解，类似(7)的证明过程，有

对(H3)和(H4)，考虑如下两种情况:

情况1 如果(H3)成立，对方程(10)两边乘以-x(t)且从0到T积分，有

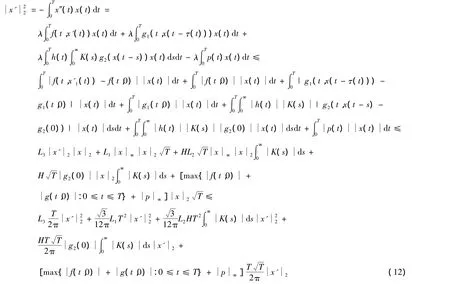
由(H3)知，存在一个常数D1使得

设t1∈［0，T］，使得=maxt∈［0，T］，则x'(t1)=0.存在常数D2满足式(14):

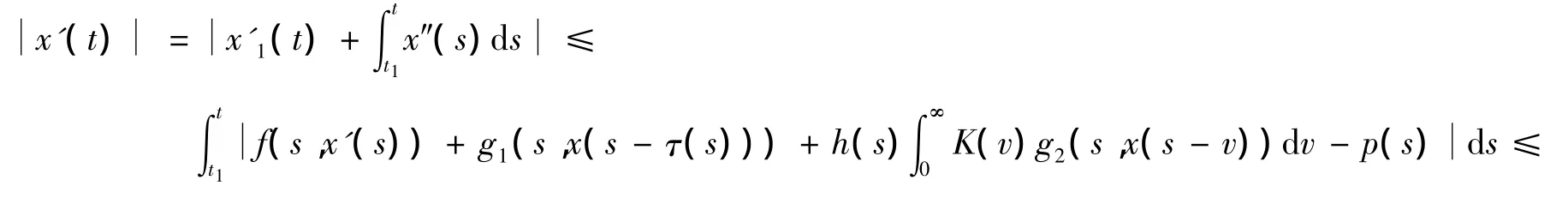
情况2 如果(H4)成立，对方程(10)两边乘以x'(t)且从0到T积分，有

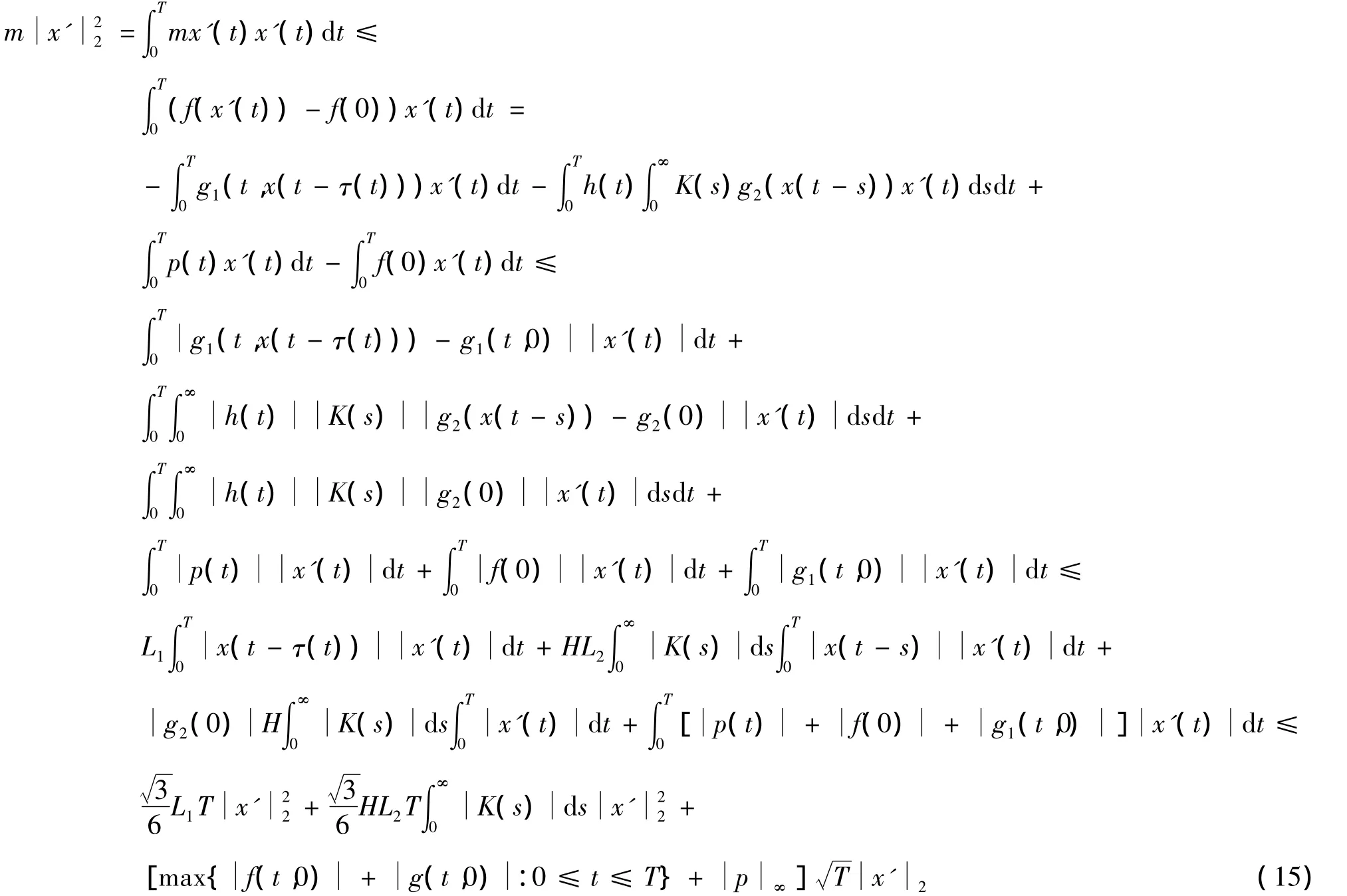
因此存在常数D3，使得

成立.

同样对方程(10)两边乘以x″(t)且从0到T积分，有

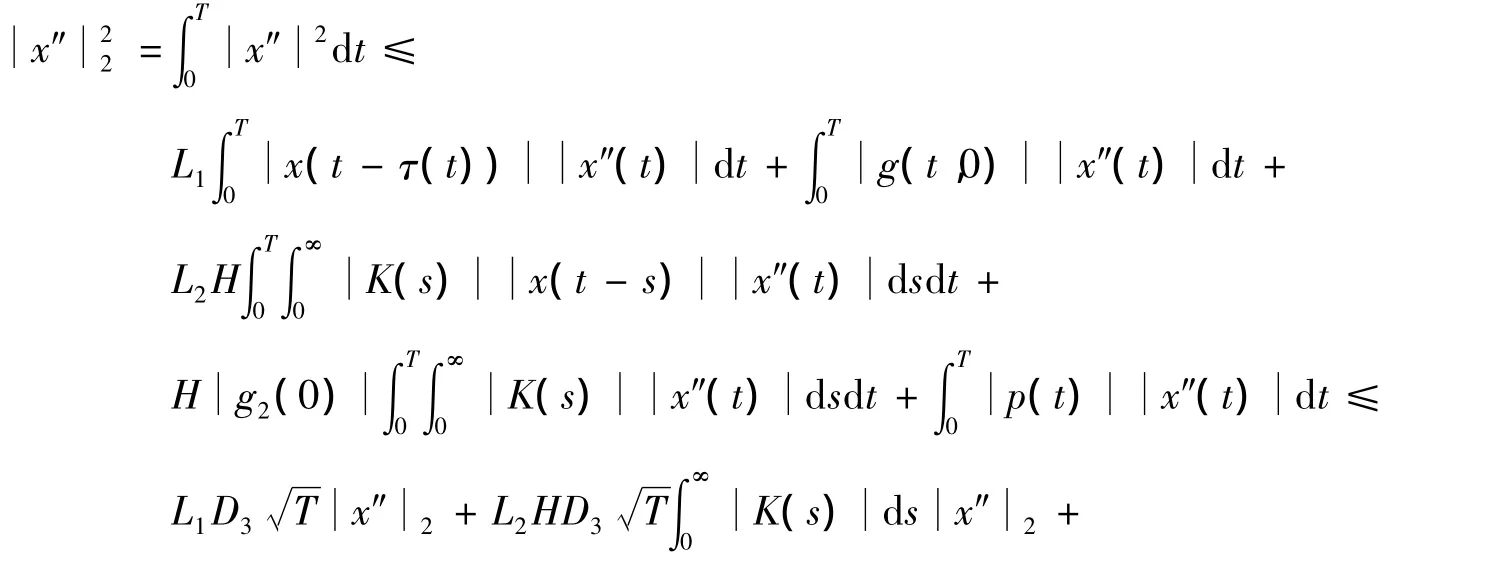
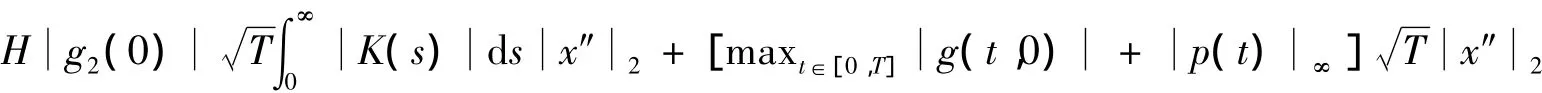
由引理3知，存在一个常数D4，使得

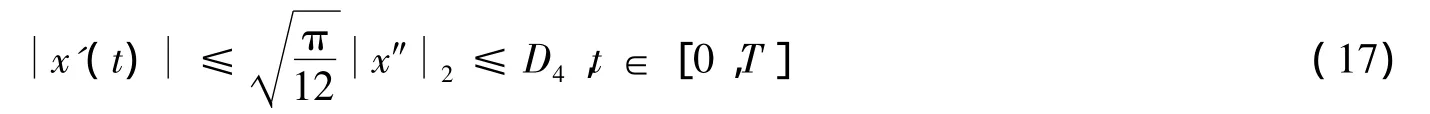
因此对式(13)(14)(16)和(17)，存在常数M1＞max{D1+D2，D3+D4}，使得 max{}＜M，设

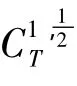
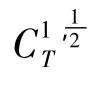
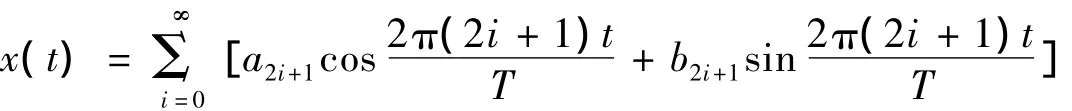
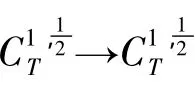
注意到

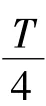
定义同伦连续场:Hμ(x):×［0，1］→，Hμ(x)=x-Fμ(x)，由 Ω 的定义知Hμ(∂Ω)≠0，λ∈［0，1］，因此，由 Leray-Schauder度的紧同论不变性知 deg{x-F1x，Ω，0}=deg{x，Ω，0}≠0.

由引理1知，方程x-F1x=0在Ω内至少有一个解，即算子F1在上有唯一反周期解.从而方程(1)有唯一的反周期解.

3 实例

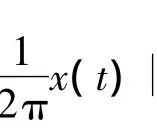
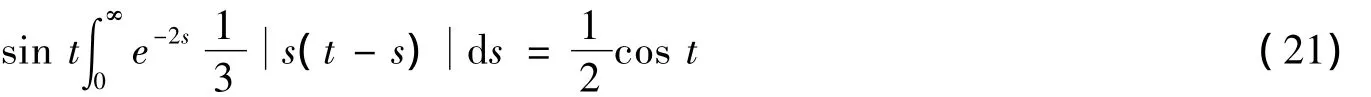
有唯一π反周期解.

容易验证方程(21)满足(H3)(H4)，因此方程(21)存在唯一反周期解.

［1］LU S，GE W.Periodic solutions for a kind of Liénard equations with deviating arguments［J］.J Math Anal Appl，2004，249:231-243

［2］MENG Y，LIU B，HUANG L H.Positive almost periodic solutions for a class of Liénard-type systems with multiple deviating arguments［J］.Journal of Computational and Applied Mathematics，2008，220:615-623

［3］GAO H，LIU B.Existence and uniqueness of periodic solutions for forced Rayleigh-type equations［J］.Applied Mathematics and Computation，2009，211:148-154

［4］ZHOU Y，TANG X.On existence of periodic solutions of Rayleigh equation of retarded type［J］.Journal of Computational and AppliedMathematics，2007，203:1-5

［5］LU S，GUI Z.On the existence of periodic solutions to Rayleigh differential equation of neutral type in the critical case［J］.Nonlinear Analysis:Theory，Methods ＆ Applications，2007，67:1042-1054

［6］ZHOU Q，LONG F.Existence and uniqueness of periodic solutions for a kind of Liénard equation with two deviating arguments［J］.J Comput Appl Math，2007，206(2):1127-1136

［7］LV X，YAN P，LIU D.Anti-periodic solutions for a class of nonlinear second-order Rayleigh equations with delays［J］.Commun Nonlinear Sci Numer Simulat，2010，15:3593-3598

［8］LIU B.Anti-periodic solutions for forced Rayleigh equations［J］.Nonlinear Anal，2009(10):2850-2856

［9］YU Y，SHAO J，YUE G.Existence and uniqueness of anti-periodic solutions for a kind of Rayleigh equation with two deviating arguments［J］.Nonlinear Anal，2009，71:4689-4695

［10］LI Y，HUANG L.Anti-periodic solutions for a class of Liénard-type systems with continuously distributed delays［J］.Nonlinear Anal，2009(10):2127-2132

［11］AIZICOVICI S，MCKIBBEN M，REICH S.Anti-periodic solutions to nonmonotone evolution equations with discontinuous nonlinearities［J］.Nonlinea Analysis，2001，43:233-251

［12］DELVOS F J，KNOCHE L.Lacunary interpolation by anti-periodic trigonometric polynomials［J］.BIT，1999，39:439-445

［13］DEIMLING K.Nonlinear functional analysis［M］.New York:Springer-Verlag，1985

［14］MAWHIN J，WILLEM M.Critical point theory and Hamiltonian systems［M］.New York:Springer-Verlag，1989