基于全通道耦合特征模型的高超飞行器控制研究*

徐李佳

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

高超声速飞行器一般是指飞行马赫数大于5的飞行器.飞行器无动力滑翔再入过程的姿态控制问题是高超声速飞行器研究领域的关键问题之一，同时也是一个研究难点.飞行器飞行过程中的各种复杂的力学过程不可能完全精细地考虑在用于控制设计的飞行器控制模型中，而且飞行过程中往往又会受到各种无法完全预知的扰动影响.这些因素直接导致了高超声速飞行器控制系统的基础结构失真、模型和参数的不确定，使得高超声速飞行器的控制问题非常具有挑战性［1-3］.

近年来，国内外学者利用鲁棒控制［4］、滑模变结构控制［5］、神经网络［6］等方法对高超声速飞行器进行了研究，并取得了一定的成果，但是针对原复杂模型设计的控制器相当复杂，运算量大，工程实现相对困难.

所谓特征建模，就是根据对象动力学特征、环境特征并与控制性能要求相结合进行建模，而不仅是以对象精确的动力学分析来建模［7］.高超声速飞行器姿态之间的强非线性、强耦合以及飞行环境的不确定导致难以建立精确的动力学模型，而特征模型却能很好地应用于这种复杂系统.

本文利用特征建模的优点，并考虑姿态3个通道之间的强耦合特性，建立一种全通道耦合的特征模型，具体结构形式包含状态之间的耦合和输入之间的耦合，在保留了原系统模型输入输出整体完整性的前提下，考虑了结构的耦合特点，更能体现原系统的内部特征，而且在此基础上设计的控制器具有很强的鲁棒性，能很好地应对高超声速飞行器飞行过程中较大的干扰影响.

1 问题描述

本文研究“类X-20”高超声速飞行器的姿态控制问题.飞行器巡航段在高空中以大于5马赫的飞行速度无动力滑翔，通过改变飞行器的姿态达到期望的受力情况.“类X-20”飞行器具有4个独立的控制舵面，即左、右副翼和左、右方向舵，本文通过设计控制器控制飞行器的舵面偏转来实现跟踪制导律所提供的姿态角指令.

假设:①飞行过程中无风;②飞行器所受外力只包含地心引力和气动力.在上述假设条件下，推导高超声速飞行器姿态动力学方程［8-9］，其中涉及到如下坐标系:地心旋转坐标系 Se，当地铅垂坐标系Su，本体坐标系Sb，气流坐标系Sa和航迹坐标系Sk，其相关定义可参考文献［9］.各参考系之间的关系如下［8］.

Se，λ为经度，φc为纬度(以赤道为零，北纬为正，南纬为负);

Su，χ为航迹方位角，方向北偏东为正，北偏西为负，γ为爬升角;

Su，φ为偏航角，θ为俯仰角，φ为滚动角;

Sb，α为攻角，β为侧滑角.

根据飞行器动力学方程可以推导得到:

攻角通道

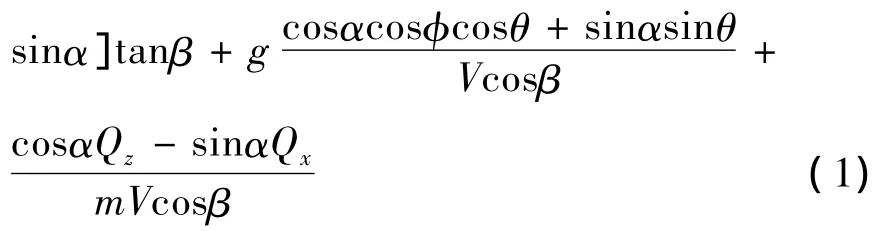
侧滑角通道

滚转角通道

三轴姿态角动力学方程为

气动力和气动力矩表达式

上述方程(1)～(9)中，ωx，ωy，ωz为飞行器本体相对于当地铅垂坐标系的转动角速度;ωuex，ωuey，ωuez为当地铅垂坐标系相对于地心旋转坐标系的角速度;Jx，Jy，Jz，Jxz为本体系下转动惯量和惯量积;g为重力加速度;ρ为大气密度;V为飞行标量速度;m为飞行器质量;S，L分别为飞行器参考面积和参考长度;CFa，CFy，CFn分别为沿轴向、侧向和法向的气动力系数;CMx，CMy，CMz为滚转力矩系数、俯仰力矩系数和偏航力矩系数.

各项气动力或气动力矩系数可以表示为基本量和由舵偏产生的气动系数增量的和，具体形式如下:

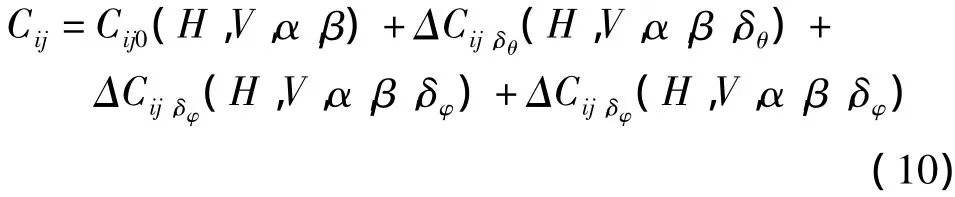
其中 i=F或M ，j=a，y，n或x，y，z，分别用于区别下标.从上式中可以看出，气动系数为飞行高度H、速度V、攻角α、侧滑角β及3个舵偏角(俯仰舵偏δθ、偏航舵偏δφ和滚转舵偏δφ)的复杂函数，工程上通过数值分析可以得到相关的拟合函数，例如在高度为40km，速度为15马赫，并忽略舵偏影响的情况下得到［8］

可见工程上的拟合函数是在一定的假设条件下得到的，而在实际的飞行过程中高度、速度、舵偏的变化都会影响气动力和气动力矩，因此事实上并不能完全忽略这些因素，下文提出的全通道耦合特征模型考虑所有通道间的耦合情况，实时辨识特征参数，具有很好的自适应和鲁棒能力，可以有效地解决上述问题.

2 特征建模及控制器设计

俯仰舵偏δθ、偏航舵偏δφ和滚转舵偏δφ可以在无动力滑翔段用于姿态的调整，因此作为控制器的3个输入量;而攻角α、侧滑角β和滚转角φ需满足一定的跟踪条件，因此作为控制器的3个输出量.

基于全通道耦合特征模型的控制结构框图如图1所示.可以看出，被控对象仍为原对象动力学模型，而控制器的设计则是基于通过辨识得到的特征模型，特征模型结构简单，便于控制器的设计.

图1 控制系统结构框图Fig.1 Block diagram of control system structure

考虑到飞行器动力学模型姿态角之间的强耦合性，首先在理论上建立攻角、滚转角和侧滑角3通道耦合的特征模型.

分析攻角通道:攻角的变化与侧滑角及滚转角之间存在耦合，而3个舵偏角的变化都会对攻角产生一定的影响，因此建立的特征模型应采用结合状态耦合及输入耦合的形式.攻角通道特征模型的推导过程是将气动力和气动力矩系数代入方程(1)～(9)，并对式(1)～(3)求导，结果可以简化定义为如下形式(具体推导过程略):

对上式离散化，采样周期为ΔT，采用如下形式的近似离散化方法:

其他参数β，φ，δθ，δφ，δφ的离散化表示形式同上，可以推得如下方程:

同理可得侧滑角和滚转角通道的离散化方程:

将式(12)～(14)写成矩阵形式，并忽略建模误差，得到全通道耦合特征模型标准形式

其中 Y(k)= ［α(k)，β(k)，φ(k)］T;U(k)= ［δα，δβ，δφ］T;

其中F1(k)，F2(k)的对角线元素在一定的投影范围内，分别接近2和－1，F1(k)，F2(k)的非对角元素代表了各通道间的耦合，G(k)阵的元素代表了舵偏对姿态的影响.因此，全通道耦合特征模型能完整地反映出原对象模型的特性，把原复杂系统的强非线性、强耦合特性转化到几个时变的耦合特征参量中，大大简化了模型的复杂程度，利于控制器的设计.

全通道耦合特征模型方程(15)中的特征参数为时变参数，不能直接给出，需要通过辨识得到，本文采用多变量梯度辨识算法进行辨识，其中特征参数向量的估计值(k)记为

梯度算法递推公式为

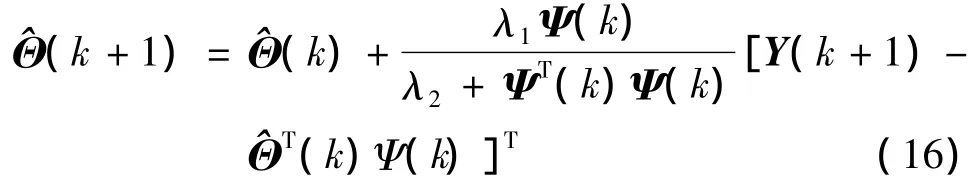
其中λ1，λ2为正常数.

通过方程(16)辨识出的特征参量，结合全通道耦合特征模型的结构，设计针对高超声速飞行器姿态控制要求的组合控制器，包含有多变量黄金分割控制律、微分控制律和积分控制律.

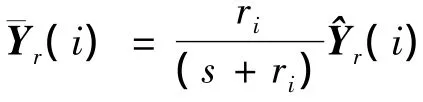
其中 ri为常数(i=1，2，3)，则 Yr(k)为柔化跟踪曲线的采样值，则误差曲线向量

多变量黄金分割自适应控制律

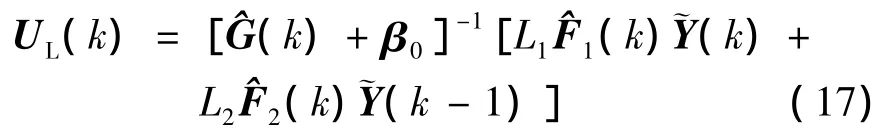
其中为了避免矩阵求逆过程中产生奇异，引入常数矩阵β0，同时选取适当的β0能保证跟踪动态过程稳定.L1，L2为黄金分割系数.文献［7］中指出，黄金分割控制律具有很好的跟踪能力及鲁棒能力.

由于跟踪初始过程和指令跳变处的抖动较明显，因此引入微分控制律，其可以有效地改善系统的动态品质，如下

其中微分系数 KD=diag{d1，d2，d3}，di为常数(i=1，2，3).

针对高超声速飞行器飞行过程中的大量不确定性扰动，采用积分控制律来消除干扰误差，如下

其中积分系数 KI=diag{c1，c2，c3}，ci为常数(i=1，2，3).

通过对对象模型的分析，得到上述控制律，综合得到总的控制量为

3 数学仿真

3.1 全通道耦合特征模型控制仿真

高超声速飞行器在无动力滑翔过程中，为使飞行具有最大航程能力，通常要求飞行器保持最大的升阻比，通过对“类X-20”飞行器气动数据分析可得，攻角在15°左右可以获得最大升阻比.仿真试验中选取如下跟踪目标:攻角保持15°，侧滑角保持0°，滚转角在 300s，700s，850s，950s处存在大范围跳变，经过一阶柔化环节后的实际跟踪曲线在下文的仿真图中用虚线表示，在初始段和指令跳变处的跟踪曲线中较明显.

被控对象主要动力学特性参数为:飞行器飞行在60km高空，初始速度标量为6000m/s，航迹方位角和爬升角设为0°，质量为4353kg，转动惯量 Jx，Jy，Jz，Jxz分别为 723.525kg·m2，34979.599kg·m2，39924.515kg·m2，996.68kg·m2.

控制器初始参数:采样时间ΔT=0.01s;辨识参数初始值1(0)=2I32(0)= －I3(0)=ΔT2I3;调节参数 λ1=0.5，λ2=0.1，r1=0.2，r2=0.8，r3=0.1，β0=diag{0.05，0.005，0.05}，KD=diag{10，200，200}，KI=diag{0.02，0.02，0.03};黄金分割系数 L1=0.382，L2=0.618;同时要求3个舵偏输入均小于30°.

(1)标称模型的跟踪控制

标称模型初始角动量均为0rad/s，滚转角、俯仰角和偏航角初始时刻均为0°，不考虑气动力矩系数、大气密度及转动惯量的不确定因素.飞行器攻角、侧滑角及滚转角的跟踪曲线如图2所示.在整个较长的飞行时间中(1000s)，姿态的跟踪效果较好，在滚转角大范围跳变的时候，攻角和侧滑角会产生微小幅值的扰动，由于全通道特征模型控制器在特征建模的时候已经把耦合因素考虑进去，因此控制器能很好地抑制滚转角对攻角和侧滑角的影响.

(2)干扰模型的跟踪控制

高超声速飞行器在飞行过程中存在很大的不确定性，因此要求设计的控制器需要具有很强的鲁棒能力.在控制器参数设定好的前提下考虑如下干扰:

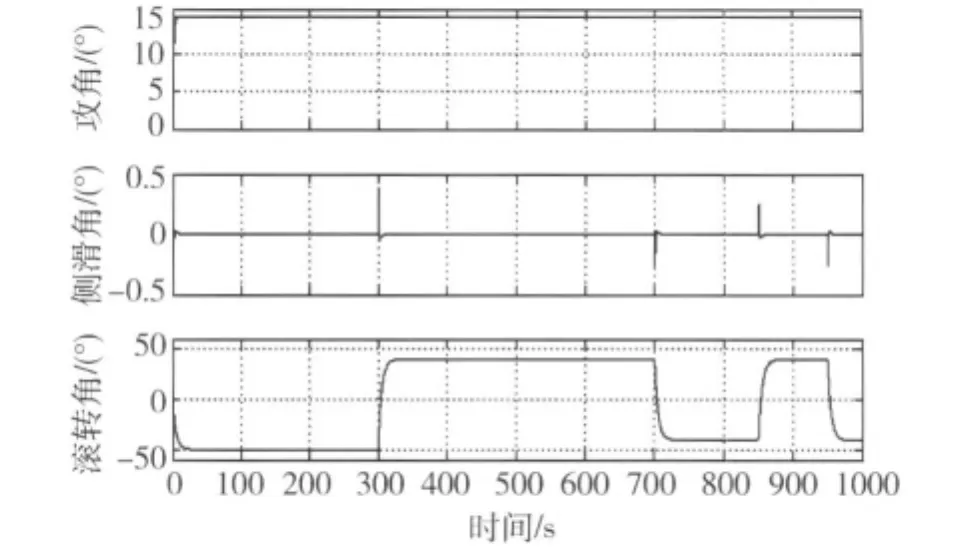
图2 标准模型的全程跟踪曲线Fig.2 Whole tracking curve of standard model

(a)参数不确定:

气动力矩系数不确定性:±30%;

大气密度不确定性:±30%;

转动惯量不确定性:±10%.

(b)初值状态干扰:

滚转角初始状态φ=10°;

俯仰角初始状态θ=5°;

偏航角初始状态ψ=5°;

角速度初始状态 ωx=ωy=ωz=0.1rad/s.

假设飞行过程中无风，飞行器速度方向即为气流方向，则攻角α，侧滑角β的初始值可由滚转角、俯仰角和偏航角的初始状态及方向余弦矩阵等式Cua=CubCba=CukCka计算出来.其中 Cua、Cub、Cba、Cuk和Cka分别为当地铅垂坐标系相对气流坐标系、当地铅垂坐标系相对本体坐标系、本体坐标系相对于气流坐标系、当地铅垂坐标系相对于航迹坐标系和航迹坐标系相对于气流坐标系的方向余弦矩阵.

从图3(a)中看出，在参数不确定和初值扰动同时存在的干扰模型下，全通道耦合特征模型控制器在长时间的飞行过程中仍能较好地实现跟踪要求.图3(b)为初始段(前50s)的跟踪曲线，在初始状态干扰下，跟踪曲线出现一些小波动后仍能快速稳定地跟踪目标曲线.图3(c)为滚转角第一次大角度跳变时(300s附近)的跟踪曲线，从图中可以看出，攻角和侧滑角受滚转角的影响在控制作用下能很快到达稳定值，即攻角维持15°，侧滑角维持0°.

通过对干扰模型的仿真研究，验证了全通道耦合特征模型控制器具有很强的鲁棒性和自适应性，是对高超声速飞行器这个复杂系统姿态控制的一种有效方法.

3.2 与单通道控制器进行比较

本文为了验证通道之间的耦合对控制的影响，通过对攻角、侧滑角及滚转角这3个通道之间的关系进行分析，并在一些假设条件下解耦，然后对各个通道单独建立特征模型，在此基础上设计单输入单输出黄金分割自适应控制律并结合微分控制律和积分控制律作用到各自通道.各通道方程如下.

图3 干扰模型下的跟踪曲线Fig.3 Tracking curve of interference model

攻角通道

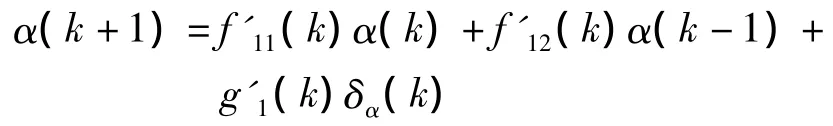
侧滑角通道

滚转角通道

其中f'ij(k)，g'i(k)为时变特征参数，可以通过梯度辨识算法得到(i=1，2，3 ，j=1，2).

控制器可以基于各个通道单独设计，下面仅给出攻角通道的控制算法.

黄金分割控制律

微分控制律

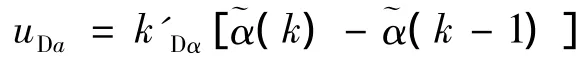
其中k'Dα为一常数.

积分控制律

其中k'Iα为一常数.

攻角通道总的控制量

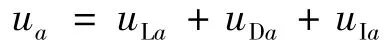
同理可得到侧滑角和滚转角通道独立的控制器，形式类似于攻角通道，这里不再详述.

对3.1节中给定的相同干扰模型进行数学仿真，结果如图4所示，(a)和(b)分别为单通道特征模型控制器初始段和指令跳变处的跟踪曲线，与图3(b)和(c)比较可以看出，单通道特征模型控制器忽略了通道之间的耦合，导致在初始段抖动较厉害，而且在滚转角指令跳变处对攻角和侧滑角的扰动较大.

通过大量的仿真比较可以看出，在一些状态平稳的飞行过程中，单通道特征模型控制器也能较好地跟踪目标，但是在飞行的初始动态段或当姿态有大幅度机动时，耦合作用就不能忽略.在仿真试验中还发现，当初始角动量较大时，耦合作用明显，单通道特征模型控制器的控制效果就不太理想，甚至完全失效;而全通道耦合特征模型控制器能充分利用各通道间特征模型的耦合参数并反馈到控制器中，产生合理的控制指令实现快速稳定跟踪.

4 结论

本文首先建立了高超声速飞行器的动力学模型，分析得出飞行器在飞行过程中三通道之间具有强耦合的特点，建立并推导了全通道耦合特征模型，其优点为:简化了原复杂的动力学模型，合理抓住了原模型各个通道之间强耦合的特点，考虑状态耦合和输入耦合，使之更接近于实际真实系统;基于此模型设计的控制器具有很好的鲁棒性和自适应性，满足飞行器飞行过程中的抗干扰要求.对精确对象模型和干扰模型进行了数学仿真研究，验证了此方法的合理性和有效性.与单通道控制器比较，发现并验证了其优越性.

图4 单通道特征模型控制器在干扰模型下的跟踪曲线Fig.4 Tracking curve of interference model with the single channel characteristic model controller

［1］ 吴宏鑫，孟斌.高超声速飞行器控制研究综述［J］.力学进展，2009，39(6):756-765 Wu H X，Meng B.Review on the control of hypersonic flight vehicles［J］.Advances in Mechanics，2009，39(6):756-765

［2］ 张靖男，孙未蒙，郑志强.高超声速武器控制技术发展探讨［J］.航空兵器，2006(4):11-13 Zhang J N，Sun W M，Zheng Z Q.Discussion of control technique of hypersonic weapon［J］.Aero Weaponry，2006(4):11-13

［3］ Fidan B，Mirmirani M，Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicle:review and new directions［R］.AIAA Paper2003-7081，2003

［4］ Gregory I M，Chowdhry R S，McMinn J D，et al.Hypersonic vehicle model and control law development using H∞and μ synthesis［R］.NASA TM-4562，1994

［5］ Xu H J，Loannou P A，Mirmmirani M.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynamics，2004，27(5):829-838

［6］ Johnson E N，Calise A J，Rysdyk R，et al.Feedback linearization with neural network augmentation applied to X-33 attitude control［C］.AIAA Guidance，Navigation and Control Conference，Denver，CO，Aug.14-17，2000

［7］ 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制［M］.北京:中国科学技术出版社，2009 Wu H X，Hu J，Xie Y C.Characteristic model-based intelligent adaptive control［M］.Beijing:China Science and Technology Publishing，2009

［8］ 龚宇莲.特征模型在高超声速飞行器控制中的应用研究［D］.北京控制工程研究所，2010 Gong Y L.Research on the hypersonic flight Vehicle control based on the characteristic model theory［D］.Beijing Institute of Control Engineering，2010

［9］ 肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2003 Xiao Y L.Modeling of aerospace vehicles［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2003