基于磁强计的卫星姿态确定地面试验*

李明群，王淑一，董 筠

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190

卫星的姿态确定是卫星姿态控制系统中至关重要的环节［1-2］，近年来，随着磁强计逐渐在新一代小卫星中获得了应用，利用磁强计的测量进行姿态确定也成为一个研究热点.磁强计具有功耗小、质量轻、无运动部件、寿命长等特点，因此由磁强计组成的姿态确定系统具有很高的可靠性，可以大大提高卫星的寿命.

目前国内的研究主要集中在理论方面，本文利用某卫星的实际遥测数据，在国内首次进行了基于磁强计的姿态确定的地面试验，试验结果定姿精度优于0.25°，表明基于磁强计的姿态确定方案合理可行.

1 姿态确定原理

1.1 基本思路

目前地磁场已经有较好的数学模型，采用高斯球谐函数来描述地磁场，地磁场的强度和矢量是位置的函数，当确定了卫星的轨道，就可以求得地磁场矢量在轨道坐标系的分量(可记为Bo).而磁强计的测量值是地磁场矢量在卫星本体的坐标系的分量(可记为Bb)，理论上两者的关系应为

式中Cbo是卫星姿态方向余弦矩阵，这样就可以在磁强计测量值与卫星姿态运动学方程之间建立数学关系，再利用滤波算法即可得到卫星姿态角.

1.2 系统状态方程

以卫星姿态运动学方程为系统状态方程，系统状态取为 x= ［φ，θ，ψ，bx，by，bz］T，其中前3 个分量分别为卫星的三轴姿态角，后3个分量分别为陀螺常值漂移，则在三轴稳定的对地定向状态下，卫星的运动学方程离散化后可以写为［1］:

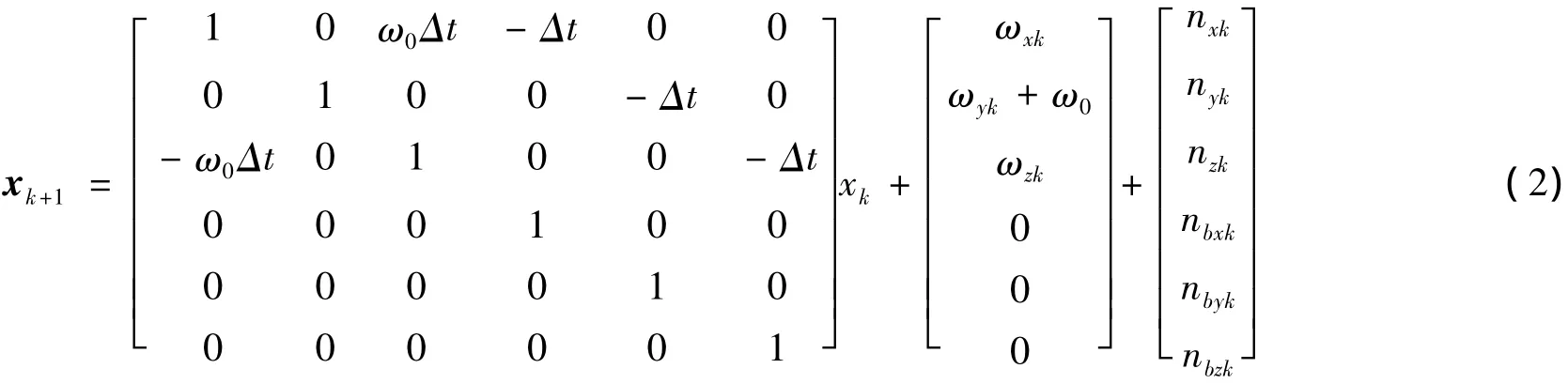
式中ω0是轨道角速度，Δt是采样时间，ωx、ωy、ωz是陀螺测量的卫星角速度三轴分量，nx、ny、nz、nbx、nby、nbz是零均值的高斯白噪声.

1.3 系统观测方程

磁强计测量方程为式(1)所示，在三轴稳定的对地定向的小姿态角状态下，姿态矩阵可以由下式替代:

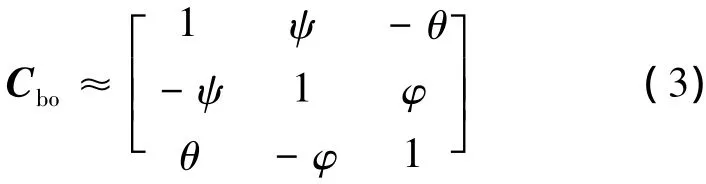
将式(3)代入式(1)，可得简化后的系统观测方程:

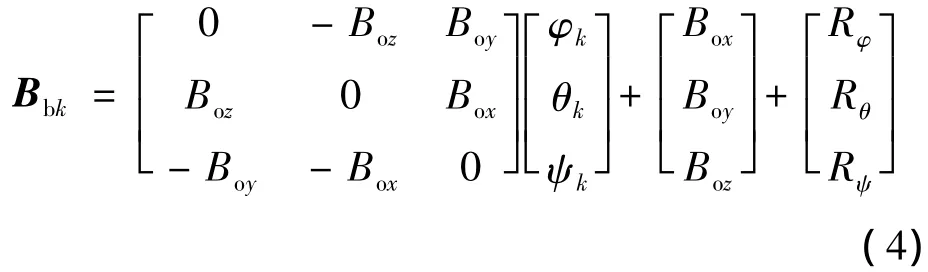
式中Rφ、Rθ、Rψ是零均值的高斯白噪声.

1.4 带遗忘因子的平方根滤波算法

卡尔曼滤波算法是常用的状态估计算法，但由于星载计算机字长有限，当卫星在轨长期运行时，计算的舍入误差会逐渐积累导致状态估计误差的方差阵失去正定性，从而导致滤波发散，为此本文采用平方根滤波算法［3］，该算法是卡尔曼滤波算法的改进算法，可以确保状态估计误差方差阵的正定性，从而适合在轨运行.该算法简述如下，对于如下系统:

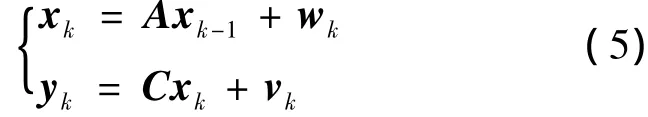
式中x为状态量，y为观测量，A和C分别为状态矩阵和观测矩阵，wk和vk为相互独立的零均值高斯白噪声，方差阵分别为Wk和Vk.则系统的时间更新方程为:

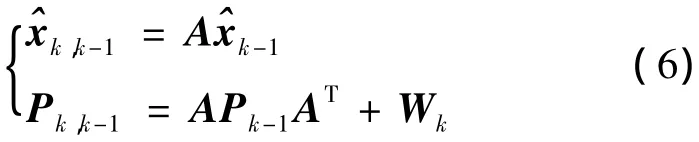
对 Pk，k－1做平方根分解，得到下三角矩阵 Δk，k－1，满足，则 k 时刻测量更新的处理按下述步骤执行:

首先取:

对于 j=1，2，…，m(m 是观测量 y的维数)，迭代计算下述方程:

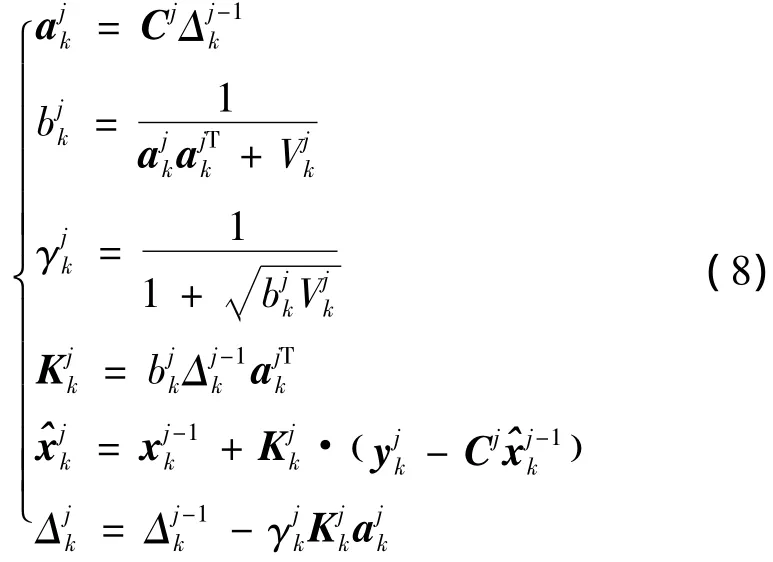
式中Cj为C阵第j行，为Vk阵对角线第j个元素，为yk的第j行.当j=m时，获得k时刻的测量更新结果如下:

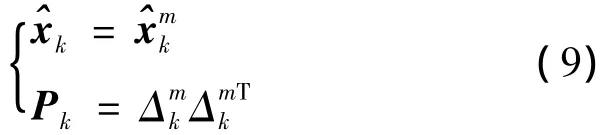
此外，为了提高新测量值的权重，在滤波器设计中引入遗忘因子λ，则式(6)中对状态误差方差阵的计算公式改写为

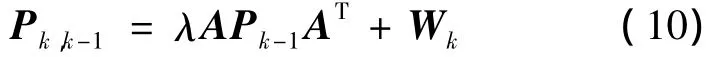
本文取 λ =0.995.

2 姿态确定地面试验

某卫星运行在高度为790km、倾角为98.7°、偏心率为0、降交点地方时为6:30AM的太阳同步轨道上，该卫星采用星敏感器进行姿态确定，运行在三轴稳定的对地定向模式，保持在零姿态附近，满足第1节中小角度的假设条件.本文利用该卫星2011年11月22日的遥测数据做了基于磁强计的姿态确定地面试验，试验方案如下:

Step1:通过解遥测包，获得磁强计的测量值、陀螺的测量值，根据地磁场模型得到地磁场矢量的理论值;

Step2:利用本文第1节的滤波算法进行姿态确定，由于遥测数据的不连续性，因此在无遥测数据的时刻，进行线性内插获得数据(卫星姿态平稳，因此较短的时间间隔内测量值可以认为是线性变化);

Step3:以星敏感器的姿态确定为姿态基准，对试验结果进行精度评价.

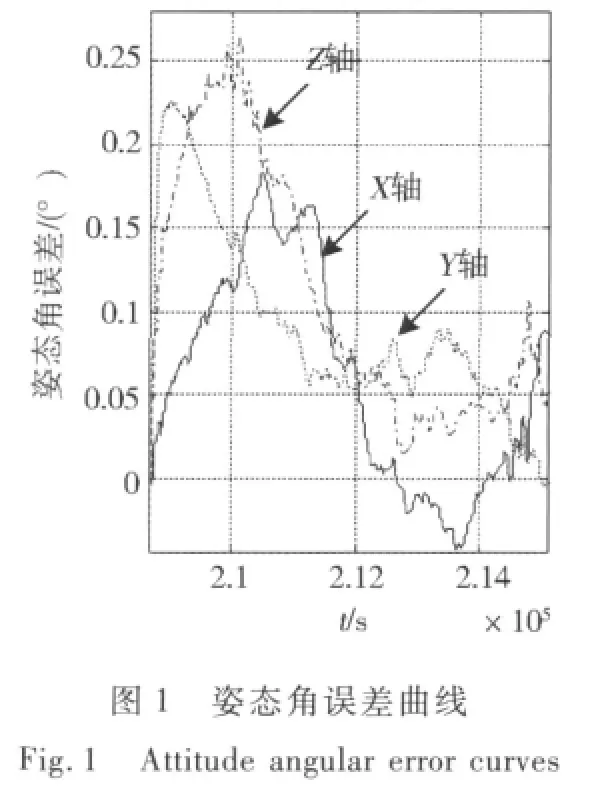
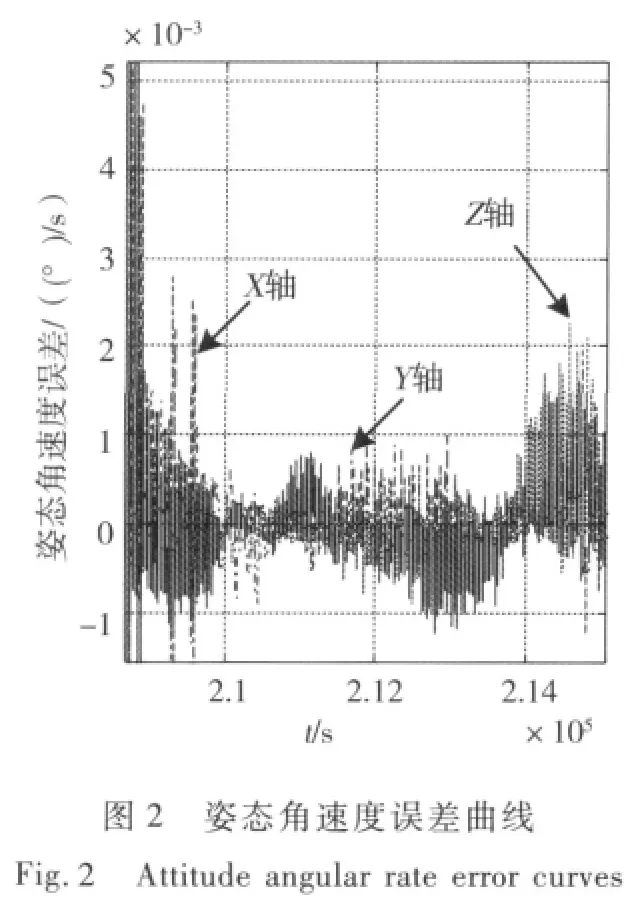
可以看出，试验中的数据来源均为星上遥测，与真实的卫星姿态确定系统相比，仅有滤波计算的地点不同，因此该方案可以很方便地移植到星上实现.地面试验结果如图1～2所示.

由图1～2可以看出，基于磁强计的滤波算法可以完成姿态确定，当以星敏感器为基准时，基于磁强计的姿态确定的姿态角误差小于0.25°，姿态角速度误差小于 0.005(°)/s.

3 结论

本文利用某卫星的飞行数据，设计了基于磁强计的姿态确定方案，并进行了地面试验，取得了较好的姿态确定精度，验证了基于磁强计姿态确定方案的可行性，具有很强的实用价值.

［1］ 章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，1998 Zhang R W.Satellite orbit and attitude dynamics and control［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，1998

［2］ 屠善澄.卫星姿态动力学与控制［M］.北京:中国宇航出版社，2005 Tu S C.Satellite attitude dynamics and control［M］.Beijing:China Astronautics Press，2005

［3］ 付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003 Fu M Y，Deng Z H，Zhang J W.Kalman filter theory and application in navigation system［M］.Beijing:Science Press，2003