基于代码自动生成的空间交会GNC系统仿真平台*

胡海霞，刘 洁，涂俊峰

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

空间交会对接是中国载人航天二期工程中已突破的一项关键技术，而建立空间交会仿真系统是保证交会任务成功的一个必备条件.国外关于空间交会仿真技术的研究已有近半个世纪的历史，从“Apollo”飞船到 ATV(automated transfer vehicle)、HTV(H-II transfer vehicle)的研制，都采用了地面模拟数字计算机仿真、实物/半实物仿真和在轨试验的研发模式［1］.数字计算机仿真将空间交会制导导航与控制(GNC)系统的所有组成部分都用数学仿真模型来描述，有不受硬件、结构和环境等条件限制的优点.

面向对象方法是开发数字计算机仿真系统的常用方法，它可以实现仿真模型和程序代码的通用性与模块化，近年来在航天领域得到了很快的发展与应用［1-4］.面向对象方法在空间交会对接数字仿真系统方面的应用，也有学者做了很多研究工作.文献［1］中介绍了空间交会对接仿真系统中的类及其对象，并简单设计了类间的关系;文献［4］在面向对象方法学的指导下，分析设计了包括地面测控在内的交会对接仿真系统的总体框架，给出了此软件系统的对象模型、动态模型和功能模型，并对这一框架进行了初步的实现.

目前大部分研究工作仅给出了仿真系统大体框架的设计思路，没有考虑空间交会仿真系统所需的大量的仿真模型如何进行接口规范，也没有考虑是否可以采用代码自动生成技术将这些仿真模型自动连成仿真程序，以减少研究人员的工作量.正是在这种背景下，本文给出一种仿真模型的规范化方法，并在此基础上，提出一套基于代码自动生成技术的空间交会对接GNC仿真平台.

1 功能与组成

空间交会对接GNC仿真平台的目标是建立起基于可靠模型的、规范的空间交会对接GNC仿真环境，能够完成目标器和追踪器的轨道动力学和姿态动力学的实时解算、相对动力学的实时解算、GNC测量设备的模拟、轨道和姿态控制模拟等，用于支持空间交会对接GNC系统的设计、分析和验证.

参与交会对接任务的两个航天器的姿态轨道控制系统均由动力学、敏感器、控制器和执行机构四部分组成，因此也决定了仿真系统可以分为动力学模型(含姿态动力学模型、轨道动力学模型、外干扰力和力矩模型)、敏感器模型(陀螺、红外、太阳、GPS、激光雷达、微波雷达等)、控制器模型(星上算法)和执行机构模型(动量轮、推力器、控制力矩陀螺(CMG)等)，除此之外，相对于单个航天器的仿真系统而言，交会对接仿真系统还增加了相对动力学模型和相对测量敏感器模型.控制系统的闭环反馈结构如图1所示.

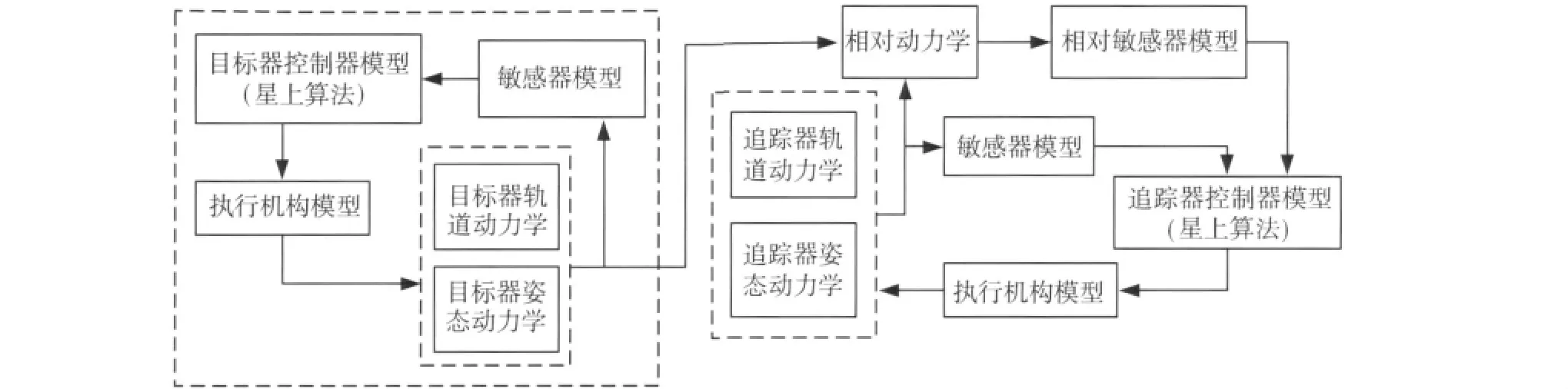
图1 交会对接GNC系统仿真结构图Fig.1 GNC system structure for rendezvous and docking

由图1可知，空间交会对接仿真平台的核心是仿真模型，包括高精度的轨道动力学模型、姿态动力学模型、相对动力学模型、敏感器模型、执行机构模型和常用基础算法模型等.所有应用于GNC系统仿真的模型都必须是经过充分验证的、可靠的模型.

下面给出空间交会对接GNC仿真平台中需要模拟的数学模型，以及各个数学模型的输入输出接口，供编写仿真模型使用.

1.1 带大附件的柔性航天器动力学模型

传统的刚体动力学模型无法准确描述航天器的动力学特性，现代的航天器大部分可以模化为中心刚体加大型柔性附件类柔性航天器.针对交会对接不断变轨的特点还要考虑姿态和轨道的相互耦合关系，这里给出系统动力学方程［5］:

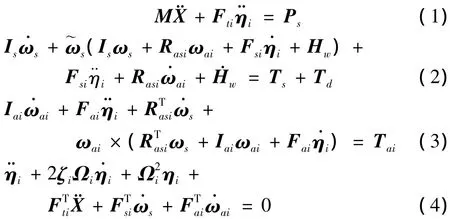
其中，M为系统质量阵，X为航天器质心相对于标称位置的摄动量，Is为系统惯量阵，ωs为中心体的角速度，ηi为各附件的模态坐标，Fti、Rasi、Fsi、Fai分别为各附件的柔性耦合系数阵，Hw为飞轮的角动量，Iai为附件的惯量阵，ωai为附件的角速度，Ps为作用在航天器上的作用力，Ts为控制力矩;Td为外扰力矩;Tai为帆板驱动力矩;Ω为模态频率对角阵.

1.1.1 姿态动力学模型

由式(2)～(4)可知，姿态动力学模型中要考虑附件的转动方程、附件转动与附件振动的耦合、附件振动与中心刚体转动的刚柔耦合、附件转动与中心刚体转动的耦合，以及航天器平动对姿态的耦合等.实时解算时还要考虑航天器质心随着燃料消耗的变化、帆板在不同转角位置时整星惯量的变化.在环境干扰力矩方面，需要考虑太阳光压、大气阻力、重力梯度力矩、剩磁力矩等.

姿态动力学模型需要配置附件挠性耦合参数、转动惯量，附件尺寸、面积，附件压心位置等参数，配置帆板驱动机构的各个参数，如电机齿数、驱动阻尼系数、驱动高次谐波力矩幅值等.

姿态动力学模型初始化:初始姿态角、初始姿态角速度、姿态转序、整星惯量阵、整星质心、附件初始转角、附件特性参数(包括附件惯量、安装位置、振动频率、阻尼比、耦合系数).

姿态动力学模型输入:轨道信息Coi、轨道角速度、解算步长、外干扰力矩、推力器输出力和力矩、动量轮角动量和控制力矩、卫星平动加速度、附件指令转速、卫星质量阵.

姿态动力学模型输出:姿态角、姿态角速度、姿态矩阵Cbo、姿态四元数、附件挠性模态及其导数、卫星惯量阵、卫星质心、附件转角.

1.1.2 轨道动力学模型

航天器轨道动力学方程如下［6］:

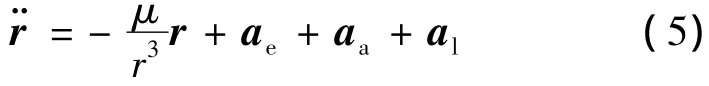
其中，r为航天器质心的标称位置，ae为地球非球形引力摄动加速度，aa为大气阻力加速度，al为太阳光压加速度。考虑帆板柔性对航天器平动的影响，将式(5)中的r和式(1)中解算的航天器质心相对于标称位置的摄动量X叠加在一起作为航天器质心的位置。

轨道动力学模型中除了所需的轨道摄动因素考虑齐全外，还应包括时间系统、日月星历计算、岁差、章动、地球自转矩阵、极移相关计算、位置速度与轨道根数相互转换函数等.

轨道动力学模型初始化:初始轨道历元、初始轨道六要素.

轨道动力学模型输入:航天器姿态、推力器推力、解算步长tstep.

轨道动力学模型输出:轨道瞬时根数、轨道系惯性系旋转矩阵Coi、质心位置速度在惯性系和地固系的表示、日月矢量在惯性系和轨道系的表示.

1.1.3 相对动力学模型

相对动力学模型包括相对姿态和相对位置计算两部分，主要是由两个航天器在惯性系的位置和姿态分别计算出相对位置和相对姿态.相对动力学模型的输出作为相对测量敏感器的输入，两者均是空间交会GNC仿真系统中必不可少的仿真模型.

相对动力学模型初始化:追踪器对接面在追踪器质心坐标系中的位置，目标器对接面在目标器质心坐标系中的位置.

相对动力学模型输入:追踪器和目标器的轨道信息、追踪器和目标器姿态旋转矩阵.

相对动力学模型输出:两航天器质心之间相对位置和相对速度，两飞行器对接面之间的相对位置、相对速度、相对姿态、相对姿态角速度等.

1.2 测量模型

1.2.1 姿态确定敏感器模型

常用的姿态确定敏感器模型包括陀螺、红外敏感器、太阳敏感器.它们应测到的真实量由姿态动力学和轨道动力学模型提供，再结合其安装方位，计算出敏感器测量坐标系下的姿态或角速度信息，然后考虑敏感器的测量噪声和采样量化问题，给出敏感器的测量值.这里以数字太阳模型为例，给出姿态确定敏感器模型的输入和输出，其他与此类似.

数字太阳模型初始化函数:安装矩阵、测量角视场范围、进光角视场范围、测量角输出的常值误差、测量噪声的均值和方差、输出当量.

数字太阳模型输入:本体系到轨道系的姿态矩阵Cbo、太阳矢量在轨道系的表示So.

数字太阳模型输出:测量角、见太阳标志.

1.2.2 相对测量敏感器模型

常用的空间交会对接敏感器有RGPS、激光雷达、微波雷达.它们应测到的真实量由相对动力学模型提供，再结合各个敏感器的安装情况，计算出在敏感器测量坐标系的测量信息，然后考虑敏感器的测量误差、测量范围、首次捕获和重新捕获的时间约束等，最终给出敏感器的测量值.这里以微波雷达为例，给出相对测量敏感器的模型输入输出，其他敏感器与微波雷达相似.

微波雷达模型的初始化函数:测距误差均值和方差、测角误差均值和方差、作用范围、视场半张角、微波雷达在追踪器上的安装位置、应答机在目标器上的安装位置、测量噪声的均值和方差、首次捕获和重新捕获的时间.

微波雷达模型的输入:本体系相对轨道系姿态角速度在本体系下的表示Wbo、追踪器的本体系到轨道系的转换矩阵Cbo、目标器质心相对追踪器质心的相对位置和相对速度在追踪器轨道系下的表示.

微波雷达模型的输出:测量目标器相对雷达的相对距离、方位角、仰角、相对速度、方位角速度、仰角速度;数据有效性标志、首次捕获的标志和计时、重新捕获的标志和计时.

1.3 控制器模型

控制器模型指的是星上控制算法，主要功能是利用航天器姿态测量信息和相对测量信息确定航天器的姿态以及两航天器之间的相对状态，由制导和控制算法给出姿态和轨道控制信号，并计算出执行机构的控制电压或开关机指令.

控制器模型的输入:各敏感器测量信息.

控制器模型的输出:发动机开关机指令和开关机时间，太阳帆板的控制转速，动力轮的控制电压.

1.4 执行机构模型

执行机构包括动量轮、CMG和推力器等.它们的模型均可抽象为初始化、输入、输出3个部分.这里以推力器为例.

推力器模型初始化:推力大小、安装位置、安装方向、安装误差、推力上升时间常数、推力下降时间常数、推力开启延时、推力关闭延时等.

推力器模型输入:发动机每个控制周期内发动机的开关机状态及开机时间.

推力器模型输出:发动机产生的控制力和控制力矩.

1.5 仿真主程序

仿真主程序的功能是将上述4类(动力学类、敏感器类、控制器类、执行机构类等)若干个仿真模型按照各类模型之间的固定输入输出关系闭环起来，形成仿真程序，供设计人员仿真使用.

2 基于VC++的GNC仿真平台方案设计

面向对象程序设计是近年来一种主流程序设计方法，其基本构件是对象与类，采用属性、消息、继承的机制实现内部管理与外部协作，其优点是对仿真系统进行抽象，并具有模块化和信息隐藏等特点，提高了系统的可重用性与可维护性［1］.GNC仿真平台采用面向对象技术设计，并出于对运行效率和通用化的考虑，利用Microsoft公司的Visual Studio 2005的C++语言进行开发.

2.1 规范化的仿真模型实现

在空间交会GNC仿真系统中，仿真模型表现为C++语言编写的具体的可执行文件或者动态链接库文件.由第2节对各类模型的功能分析可知，所有模型均可由两个函数来实现，即初始化函数和解算函数.

2.1.1 初始化函数

初始化函数的定义方法为:将初始化函数中的参数采用宏变量表示，形式为:

参数:x，y，z;

模板:MYM(mod_name).init(MYM(x)，MYM(y)，MYM(z));

参数x、y、z为动力学类仿真模型、或敏感器类仿真模型、或执行器类仿真模型的安装坐标，mod_name为动力学类仿真模型、或敏感器类仿真模型、或执行器类仿真模型的名称，init为初始化函数.

2.1.2 解算函数

解算函数中的参数采用宏变量表示，形式为:

参数:a_in，a_out;

模板:MYM(mod_name).Solve(MYM(a1_in)，MYM(a1_out));

参数a_in为本仿真模型的输入，a_out为本仿真模型的输出;mod_name为动力学类仿真模型、或敏感器类仿真模型、或执行器类仿真模型的名称;Solve为解算函数.

2.2 仿真模型描述文件

仿真模型描述文件以VC++开发环境可以识别的方式描述模型使用方法，它可以用来指导开发环境完成代码自动生成.一个开发人员要使用一个模型，需要读懂模型的源代码或者模型的说明文档.对于开发环境来说，要直接解析源代码或说明文档是不现实的，因此考虑使用描述文件这种间接的方式，用于描述模型的一些名称、版本、初始化和解算函数的信息.模型描述文件由仿真模型的编写者来完成，仿真平台提供专门的描述文件编辑器可以生成规范的模型描述文件.

模型编写者可以将每个仿真模型的初始化代码和解算代码抽象化，提炼成代码模板，代码中需要特殊化的部分用宏变量代替，如图2所示的数字太阳仿真模型的描述文件.

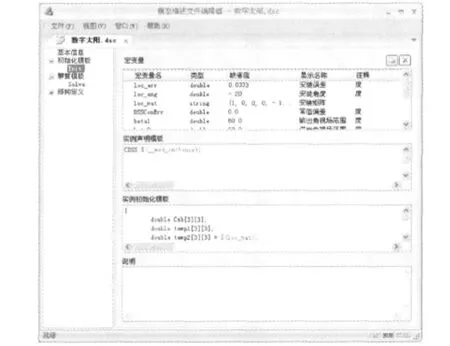
图2 仿真模型描述文件示意图Fig.2 Graph of simulation model description file

下面以一个实例来说明.某个模型使用矩阵来进行初始化，初始化代码为:

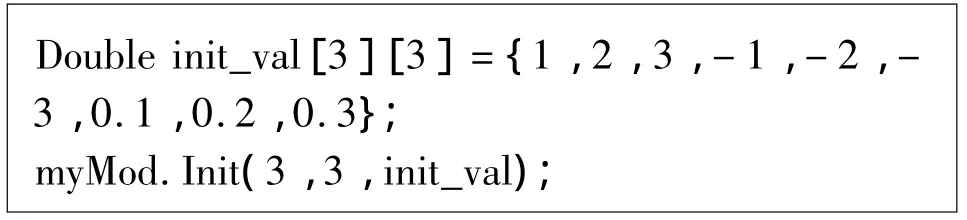
模型编写者允许用户配置矩阵的行数、列数和初始值，分别使用宏变量$(mx_row)、$(mx_col)、$(mx_init_val)来代替，模型实例的名称用宏变量$(__mod_instance)来代替，提炼出代码模板为

在代码自动化生成工具模型的使用者通过配置界面给宏变量赋值，代码自动化工具就能根据模板和宏变量的值生成初始化代码.

自动化工具根据使用者的实际配置的参数将上面的模板展开，就可以还原成例子中的代码.所有模型的代码组合到一起就成为最后的VC++工程，2.3节将详细展开说明代码自动生成的过程.

2.3 代码自动生成工具

采用描述文件编辑器把所有的仿真模型描述完成之后，设计人员可以在操作界面上对所选的模型进行初始化设置，设置完成后利用代码自动化生成工具就可以自动生成仿真流程代码，最终生成一个VC++工程.

2.3.1 初始化代码的自动生成

仿真初始化代码是所选的所有仿真模型的初始化代码的组合.对于单个模型，其初始化方法通过模型的描述文件定义，初始化方法定义包括参数和模板两部分，如敏感器模型S，其初始化方法定义是:

参数:x，y，z

模板:$(mod_name).init($(x)， $(y)，$(z));

参数x、y、z为敏感器模型S的安装坐标，参数mod_name为模型的实例名称，设计人员在建模工具中可以设置这些参数的实际值，自动化生成技术将初始化模板中的参数用实际值代替，就可以生成模型的初始化代码.

2.3.2 仿真主循环代码的自动生成

在生成仿真主循环时，自动代码生成主要解决下列问题:

(1)模型解算顺序

仿真主循环代码为for循环结构，在循环中各模型实例按动力学类、敏感器类、控制器类、执行器类的顺序依次解算(如图3所示).

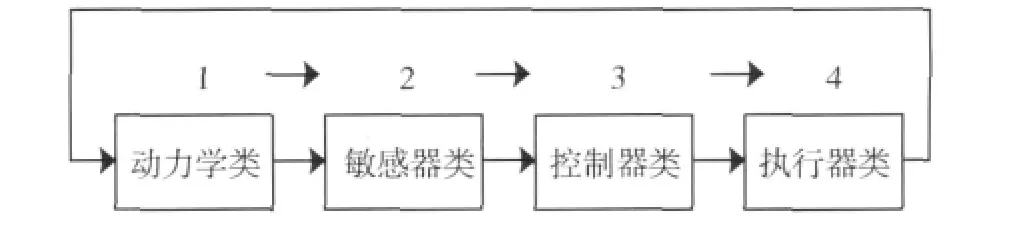
图3 控制系统接口关系图Fig.3 Graph of relationship between control system interfaces

(2)主循环步长

主循环步长是以毫秒为单位的整数，是所有模型实例步长的最大公约数，当前仿真时间在主循环中每次递加一个主循环步长.

(3)每个模型解算条件

模型并不是每个主循环都解算，只有在当前仿真时间为模型仿真步长的整数倍时才解算.

(4)建立参数传递关系

规定参数传递方向为:动力学类输出参数给敏感器类，敏感器类输出参数给控制器类，控制器类输出给执行器类，执行器类输出给动力学类.传递规则为:如果模型A和B在类别上符合参数传递方向，且模型A的某个输出参数X的关键字与模型B的某个输入参数Y的关键字相同，视为X与Y匹配，那么自动生成的代码中传递给参数X和Y的将是同一个变量.

举例来说，如图4所示，有动力学模型D1，敏感器模型S1和S2，由于动力学类对敏感器类构成输出关系，而D1的输出参数关键字为para_key_x，S2的第一个输入参数的关键字也是para_key_x，可以匹配.

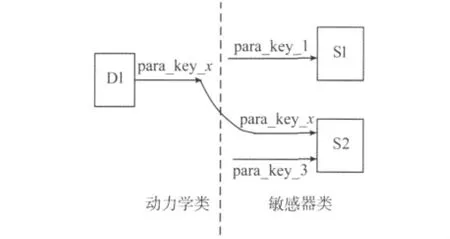
图4 动力学模型参数传递关系匹配图Fig.4 Matching graph of dynamics model parameter transfer relation

(5)控制器接口函数

控制器模型并非来自模型库，而是自动生成接口函数后再由设计人员增加实际的星上算法代码.

生成的控制器模型没有初始化函数，只有解算函数，函数为空，代码将来由设计人员填写.生成控制器接口的主要工作是获取其解算函数的输入输出参数，规则为:所有敏感器模型的输出作为控制器的输入，所有执行器的输入就是控制器的输出.所以获取所有敏感器模型的输出和所有执行器模型的输入就构成了控制器解算函数的参数列表.

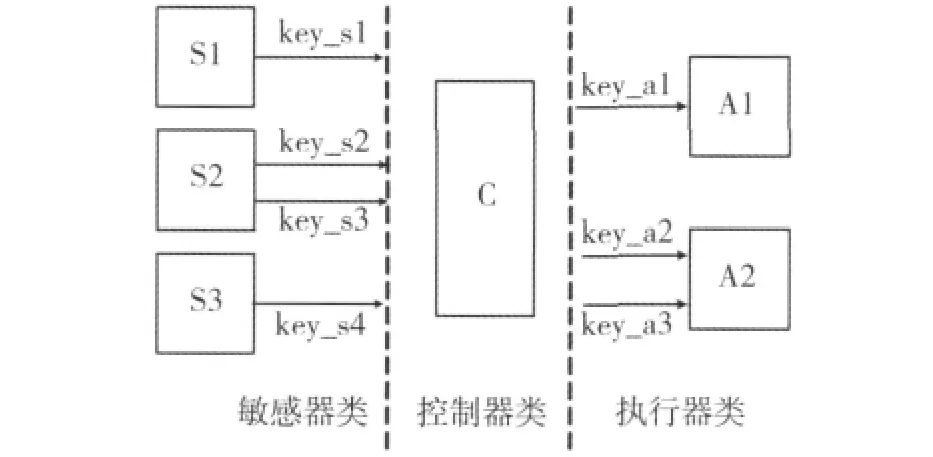
图5 敏感器模型参数传递关系匹配图Fig.5 Matching graph of sensor model parameter transfer relation

举例来说，如图5，系统中有敏感器模型S1、S2、S3，有输出参数 key_s1、key_s2、key_s3、key_s4，执行器模型 A1、A2，有输入参数 key_a1、key_a2、key_a3，那么生成的控制器解算函数输入为key_s1、key_s2、key_s3、key_s4，输出为 key_a1、key_a2、key_a3，用模板表示为:

2.3.3 Windows程序框架及VC工程的生成

对于同样的模型选择配置，GNC仿真平台开发环境可以根据用户的需要生成不同类型的VC++工程，如控制台程序、对话框程序和单文档窗口程序.VC++工程类型不同导致最后生成的工程源文件差异很大，但是这些文件中主要代码片段:模型的实例声明、初始化、解算代码是相同的.所以生成过程分为共性的代码生成阶段和个性的文件生成阶段.

代码生成阶段由代码生成器来完成，即是2.3.1节和2.3.2节所述内容，具体工作:

1)根据用户选择的模型建立模型之间的输入输出关系;

2)根据用户选择的敏感器和执行器模型生成控制器模型;

3)根据模型的依赖关系搜索隐式包含的模型;

4)生成各模型的实例声明、初始化、解算代码，拼接成仿真程序的声明、初始化、解算代码片段.

文件生成阶段由文件生成器来完成，具体工作:

1)创建VC++工程目录;

2)下载所有模型的描述文件并解包;

3)将描述文件解包后的文件分类添加到VC++工程中;

4)用代码片段替换到源代码文件中的宏变量得到最终的代码.

自动生成方法根据已生成的仿真初始化和仿真主循环代码，再加上典型的windows程序框架代码，就得到空间交会GNC仿真平台的代码，最后将生成的代码文件以及各模型的实现文件添加到VC++工程文件从而生成完整的VC++工程，用VC++可以直接打开和编译此工程，结果就可以得到空间交会GNC仿真平台的执行程序.

3 GNC系统仿真平台实现

基于上述规范的仿真模型库和代码自动化生成技术开发了空间交会对接GNC仿真平台.

这里以某典型空间交会任务的仿真为实例，给出基于该任务的GNC数学仿真系统的仿真和数据显示结果.最终仿真软件的运行情况如图6～10所示.图6是仿真数据的显示情况，实时显示了包括地面追踪器姿态、姿态角速度、星上追踪器估计姿态、估计姿态角速度和星上段标等数据，图7～10是以图形曲线的形式显示了仿真过程中追踪器和目标器的相对位置、相对姿态、相对姿态角速度以及追踪器挠性模态的变化情况.

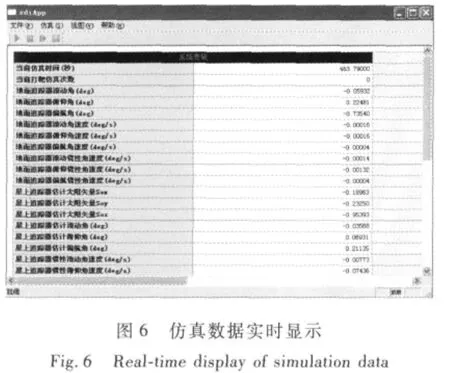
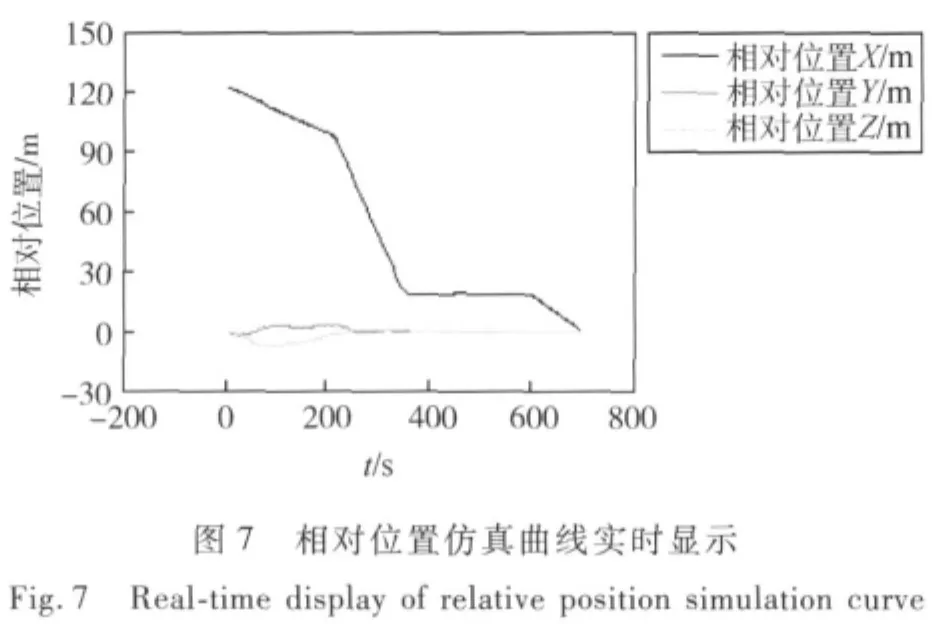
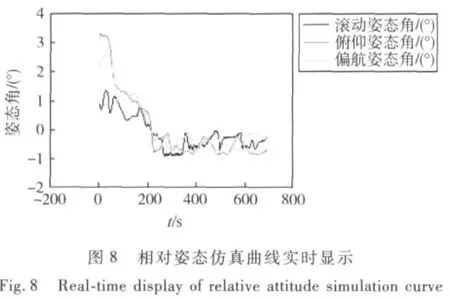
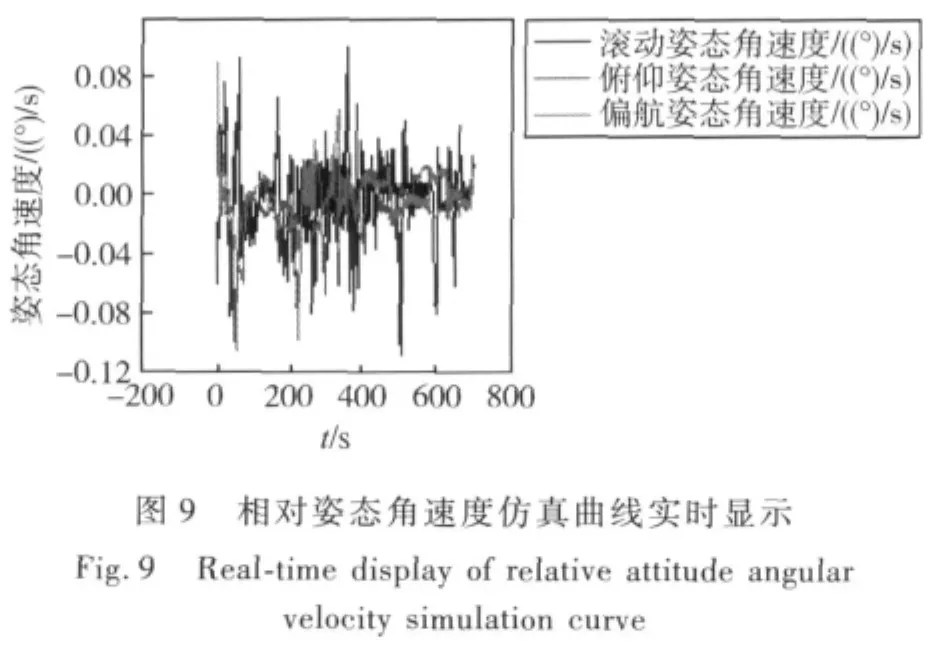
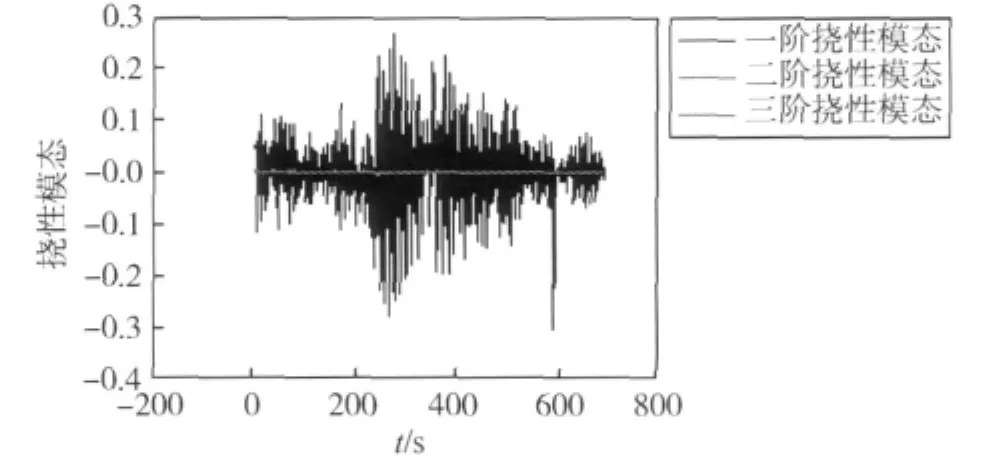
图10 追踪器前三阶挠性模态仿真曲线实时显示Fig.10 Real-time display of chaser’s first 3 order flexible modes

由上述应用实例可以看出，空间交会GNC仿真平台的成功开发及正确的仿真结果证明了基于VC++的GNC仿真平台方案合理可行.

4 结论

空间交会对接任务对GNC系统仿真提出了更高的要求.本文基于规范化模型和自动代码生成技术，设计开发了空间交会对接GNC系统仿真平台.该平台所采用仿真模型的规范化方法具有通用性好、继承性强等特点，除此之外，代码自动生成技术在仿真平台中的成功应用显著提高了设计和仿真人员的工作效率，为交会对接复杂任务的系统仿真验证提供了有力的支持.本平台的设计思路对常规卫星姿态控制乃至星群星座控制领域的数学仿真系统有一定的借鉴意义.

［1］ 刘鲁华，汤国建，余梦伦.空间交会GNC仿真系统建模中的设计模式［J］.系统仿真学报，2007，19(23):5389-5391 Liu L H，Tang G J，Yu M L.Design patterns of GNC simulation system modeling in spacecraft rendezvous mission［J］.Journal of System Simulation，2007，19(23):5389-5391

［2］ 罗亚中，唐国金，王峰，等.运载火箭优化设计通用仿真类库设计与开发［J］.系统仿真学报，2003，15(7):962-965 Luo Y Z，Tang G J，Wang F，et al.The design and development of the all-purpose simulation class library for launch vehicle optimization design［J］.Journal of System Simulation，2003，15(7):962-965

［3］ 刘鲁华，汤国建，余梦伦，等.基于UML方法的空间交会 GNC仿真系统设计［J］.计算机仿真，2007，24(10):56-59 Liu L H，Tang G J，Yu M L，et al.Design of spacecraft rendezvous GNC simulation system based on UML［J］.Computer Simulation，2007，24(10):56-59

［4］ 王华，唐国金.基于面向对象的RVD仿真系统的分析与设计［J］.计算机仿真，2003，20(5):25-27 Wang H，Tang G J.The analysis and design of RVD simulation system based on object-oriented method［J］.Computer Simulation，2003，20(5):25-27

［5］ 曲广吉.航天器动力学工程［M］.北京:中国科学技术出版社，2000 Qu G J.Spacecraft dynamics engineering［M］.Beijing:China Technology Publishing Company，2000

［6］ 刘林.航天器轨道理论［M］.北京:国防工业出版社，2000 Liu L.Spacecraft obit theory［M］.Beijing:National Defence Industrial Publishing Company，2000