曲轴内铣切削用量优化

任小中，张 坚，，王质明

(1.河南科技大学机电工程学院，河南洛阳471003;2.河南柴油机重工有限责任公司，河南洛阳471000)

0 前言

曲轴铣削作为国际上曲轴批量加工的主流技术已经得到了广泛的应用。当加工铸钢或合金钢材料的曲轴时，曲轴内铣与外铣、车铣复合技术相比，在加工余量、精度和效率等方面有着明显优势［1］。而在切削速度、加工连续性、加工精度、简化工装等方面，曲轴内铣有着传统的曲轴车削技术无法比拟的优势。但由于中国的曲轴铣削工艺推广速度较慢，对曲轴内铣切削用量优化问题研究的较少，企业在生产过程中难以充分释放内铣设备的产能［2－3］。本文针对曲轴内铣工艺，完成了切削用量优化与曲轴加工测试，提高了设备生产效率。

1 数学模型建立

1.1 建立铣削用量模型

曲轴内铣的铣削用量优化是基于其加工特点，通过对铣削加工过程的分析与研究，建立合理、准确的铣削用量优化数学模型［4］，选取目标函数(本文选取最大切削效率，在切削过程中，切削效率等同于生产效率)，采取合适的优化算法，在铣削用量的可行域内，求得目标函数最优解。

在曲轴加工中，主轴转速、切削深度、切削宽度、进给速度等切削参数，不仅作为影响曲轴铣削加工目标的因素，同时也是曲轴铣削的基本控制量。在实际生产中，切削用量优化的目标函数一般为最大切削效率、成本、刀具寿命［5］。这里将目标函数定为最大切削效率，即单件生产所需的最短时间。影响该目标函数的两个因素分别为切削速度v和单齿进给量af［6］。将最大切削效率作为优化目标时，目标函数可以表示为

式中，F(x1，x2)为单件生产所需的时间;x1为切削速度;x2为单齿进给量;D为内铣刀盘直径;L为切削长度;z为内铣刀盘齿数。

1.2 设定约束条件

在计算曲轴铣削用量时，设备效率、刀具选择、工件材质及加工质量等技术条件，都直接影响铣削用量的选择范围。因此，在优化设计计算过程中，必须考虑这些条件对铣削用量选择的限制。最终确定铣削用量时，不仅应该保证工件质量达到工艺要求，还应当做到在工艺系统强度和刚性允许的前提下，充分发挥出设备功率与刀具切削性能［7］。

1.2.1 进给速度Vf对单齿进给量af的约束

与af对应的进给速度Vf须介于最小进给速度Vfmin与最大进给速度Vfmax之间。其函数关系可表示为

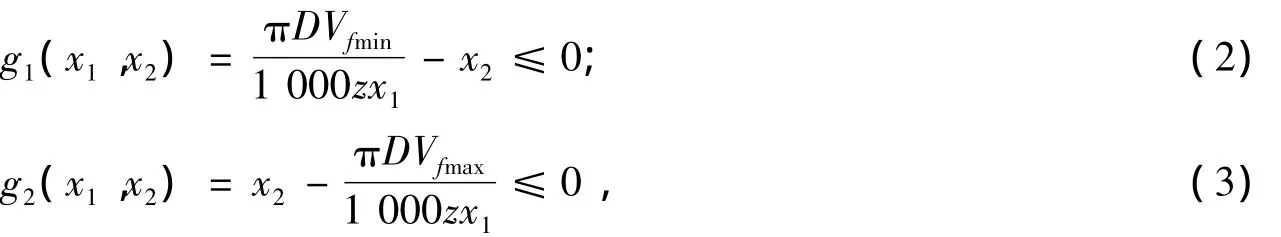
式中，g1(x1，x2)表示与Vfmin对应的单齿进给量小于实际单齿进给量;g2(x1，x2)表示与Vfmax对应的单齿进给量大于实际单齿进给量。

1.2.2 主轴转速n对切削速度v的约束

与v对应的主轴转速须介于最小主轴转速nmin与最大主轴转速nmax之间。其函数关系可表示为

式中，g3(x1)表示与nmin对应的切削速度小于实际切削速度;g4(x1)表示与nmax对应的切削速度大于实际切削速度。

1.2.3 切削进给力F对切削速度v和单齿进给量af的约束

与af对应的切削进给力F不得超过最大切削进给力Fmax，即

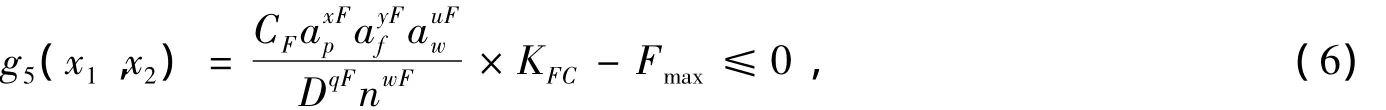
式中，g5(x1，x2)表示Fmax大于与实际单齿进给量对应的切削进给力;xF、yF、qF、uF、wF、CF、KFC为切削力因数;n为刀盘转速，n=1 000x1/(πD)。

1.2.4 切削扭矩M对切削速度v和单齿进给量af的约束

与af对应的切削扭矩M不能超过最大切削扭矩Mmax，即

式中，g6(x1，x2)表示Mmax大于与实际切削进给力对应的切削扭矩;F为圆周切削力。

1.2.5 机床功率P对切削速度v和单齿进给量af的约束

与af对应的机床功率不能超过机床最大功率Pmax，即

式中，g7(x1，x2)表示Pmax大于与实际切削进给力对应的切削功率;η为机床传动效率。

1.2.6 表面粗糙度Ra对单齿进给量af的约束

与af对应的表面粗糙度Ra不能超过工件允许的最大表面粗糙度Ramax，即

式中，g8(x2)表示最大单齿进给量小于与最大表面粗糙度对应的单齿进给量;rε为刀尖圆弧半径。

2 确定优化方案

当选取目标函数为最大切削效率时，目标函数的影响变量包括切削速度v和单齿进给量af，需对目标函数进行多目标优化。根据式(1)～式(9)，所求的全局最优解问题可视为:要求在各约束条件可行域内，找出一组设计变量X，且该点函数值等于整个可行域内的最小函数值。但由于目标函数与约束条件组成了一系列非线性方程，其优化模型具有多线性多峰值的特点，进行优化设计时容易陷入局部最优解，因此本文采用均匀布点法，通过设置多个初始点，将全局划分成多个局部，从而得到一系列局部最优解。在对求出全部解进行比较后，选取所有局部最优解中的最小值，即可得到全局可行域内的最优解。

由于优化运算量较大，本文运算时选用Matlab的工具箱函数［8］。先把全局划分成若干个局部，采取传统优化方法进行计算，求出各个局部范围内的最优解;然后在全部解中通过逐个分析比较得出最小值，即为式(1)在全局可行域内的最优解。该组解对应的设计变量X就是所求的切削用量优化结果。

实际生产过程中，对于切削用量的优化结果，往往要在试加工后再对一些函数变量进行调整，从而对优化结果进行修正［9］。

3 实例分析

3.1 加工实例

欲在一数控曲轴内铣机床上粗铣曲轴各轴颈。已知曲轴材料为42CrMoA，HB290±5，毛坯轴颈平均半径为84 mm;本道工序铣削深度ap=4 mm，要求加工后Ra=25μm;采用镶片三面刃盘铣刀，刀片数Z=12，刃口半径rε=1 mm，刀盘厚度aw=10 mm，直径D=280 mm;曲轴内铣机床性能参数见表1，按照最大生产效率选取切削参数。

表1 曲轴内铣性能

3.2 优化求解

表2 切削力因数

将已知条件以及表1中的参数带入约束条件式(1)～式(9)，将表2中的参数带入式(6)后，即得该实例的优化模型。

根据优化模型可知，75≤x1≤150，0≤x2≤ 1.26。为避免陷入局部最优解，此处选取多个起始点进行运算［10］。其中，x1的初始值x01取{75，95，110，120，135，150}，x2的初始值x02取{0.01，0.10，1.00，1.26}，两者组合后可以得到24组初始值。

选取Matlab的工具箱函数，根据初始值x01与x02得出优化结果x1与x2(见表3)。

表3 不同初始值对应的优化结果

根据表3优化结果可知:目标函数最小值为F(x)=52.78 s。根据设备特点，在表3中选取具备最大切削速度与最小单齿进给量的优化结果:切削速度x1=132 m/min，每齿进给量x2=0.167 mm。

4 结论

按照优化结果选取的切削用量，进行8件曲轴试切的切削总时间为423 s，平均每件切削时间为53 s，曲轴尺寸精度与表面粗糙度均满足加工要求。优化结果与根据经验制定的切削参数(企业生产中单件切削时间63 s)相比，单件切削时间下降了15.8%，设备生产效率有了明显提高。

通过使用计算机对曲轴内铣进行切削用量优化设计，可以快速、准确地求得最佳切削用量。但应当注意到，某些随机性因素(例如加工设备的动态特性、材料性能的变化、刀具切削磨损、各类热变形等)可能直接影响最优铣削用量的计算结果。因此，在实际生产过程中，应随时注意外部随机因素的变化，减小计算数据与实际情况之间的偏差。

［1］ 周来宏.曲轴加工工艺及曲轴内铣技术的研究［D］.大连:大连交通大学，2008.

［2］ 周浩，杜长龙.基于改进遗传算法的数控加工切削用量优化［J］.机床与液压，2011(5):57－59.

［3］ 阎长罡，于建斌.MATLAB在切削用量优化中的应用［J］.机械设计与制造，2009(2):81－83.

［4］ 任小平，刘战强.切削用量优化模型的建立及应用［J］.工具技术，2010(5):39－41.

［5］ 冯涛，杨福增，李敏通，等.基于均匀布点的铣削用量优化［J］.西北农林科技大学学报:自然科学版，2010(10):216－219.

［6］ 杨叔子.机械加工工艺师手册［M］.北京:机械工业出版社，2002.

［7］ 王先逵，艾兴.机械加工工艺手册(铣削、锯削加工)［M］.北京:机械工业出版社，2008.

［8］ 舒洲，黄宗南.基于变性遗传算法的切削用量优化［J］.机电工程，2005(1):40－44.

［9］ 张何军.曲面数控铣削加工动态仿真研究［D］.武汉:华中科技大学，2007.

［10］ 冯锦春.基于遗传算法的切削用量优化研究与实现［J］.机械设计与制造，2009(7):226－228.