无约束连续全局优化的一个无参数变换函数算法

尚有林，黄志勇，徐翠霞

(河南科技大学数学与统计学院，河南洛阳471003)

0 前言

填充函数算法［1－8］、打洞函数算法［9－11］、积分水平集法［12－13］等确定性算法都是解决全局优化问题的有效方法。但是，填充函数算法和打洞函数算法都遇到了一个很难解决的问题:如何判定当前局部极小点的全局性和类别，而且，利用填充函数算法和打洞函数算法求得的全局极小点是一个近似的全局极小点。虽然积分水平集法是为解决上述问题而提出的，但从已有的文献中可以看出:积分水平集方法解决上述问题还存在着诸多的问题，有待于完善和改进。

本文致力于解决这个问题，提出了一个变换函数算法。利用该变换函数的性质判定当前局部极小点的全局性及类别，即判定当前局部极小点是唯一的全局极小点还是其中一个相对全局极小点，并利用得到的相对全局极小点列找到原问题的绝对全局极小点。

1 假设和定义

考虑以下无约束连续全局优化问题

这里f:RnR连续可微的。

下面给出关于问题(1)如下假设及相关定义。

假设1 f(x)在X上Lipschitzian连续，即对于所有x，y∈X，有

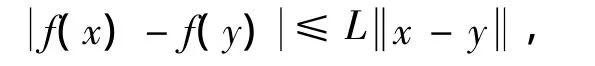
式中，L称为Lipschitzian常数。

由假设2知，在Rn上一定存在一个有界闭箱X，使得f(x)的任意极小点都在X的内部。则问题(1)等价于一个箱子约束连续全局优化问题

式中，X={x∈Rnai≤xi≤bi，i=1，2，…，n }，其中，ai，bi∈R。

假设3 f(x)在X上仅有有限个极小值。

给出有别于水平集［14］的一些新的定义:

定义1 设x*是f(x)在X上的一个当前局部极小点，若集合L0(x*)满足

则称集合L0(x*)是f(x)在x*处的去心水平集。

定义2 设x*是f(x)在X上的一个当前局部极小点，若集合L'(x*)满足

则称集合L'(x*)是f(x)在x*处的严格水平集。

定义3 在执行某个全局优化算法时，随着容许误差εi的选取不同的值，得到极小点列{x}和极小值列{f(x)}，若=x*且f(x)=f(x*)，其中x*∈X(X是可行域)，则称该全局优化算法是收敛的。x称为相对于容许误差εi的全局极小点，简称为相对全局极小点，f(x)称为相对于容许误差εi的全局极小值，简称为相对全局极小值，x*称为绝对全局极小点，f(x*)称为绝对全局极小值。

既然X在Rn上是有界闭箱，故X是紧集。水平集L(x*)={x∈Rnf(x)≤f(x*)，x∈X }包含在紧集X中。显然，L(x*)是有界闭集。所以f(x)在L(x*)存在全局极小点。

2 无参数变换函数

本文提出关于问题(2)的一个无参数变换函数为

式中，x*是f(x)在X上的一个当前局部极小点，且x∈L0(x*)。

下面将研究该变换函数具有的一些性质。

定理1 P(x，x*)在非空去心水平集L0(x*)上是连续可微的。

证明 设x∈L0(x*)，有

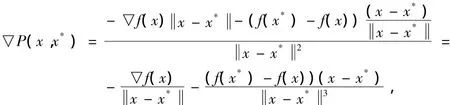
因此，P(x，x*)在L0(x*)上是连续可微的。

由于L'(x*)⊂L0(x*)，因此，P(x，x*)也在L'(x*)上是连续可微的。

定理2 P(x，x*)在非空去心水平集L0(x*)上是有界的。

证明 设L0(x*)是非空的，根据假设1可知，有

因此，P(x，x*)在非空L0(x*)上是有界的。

定理3 设严格水平集L'(x*)非空，则P(x，x*)存在且不为零。

证明 设L'(x*)是非空的，因此，至少存在一点∈L'(x*)使得f()＜f(x*)，故∈L0(x*)，有

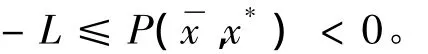
定理4 设P(x，x*)是由式(3)定义的，则L0(x*)是空集当且仅当P(x，x*)不存在。此时，) x*是f(x)在X上的一个唯一全局极小点。

以上两种情形均说明L0(x*)非空，这与题设矛盾。

必要性:设L0(x*)是空集，即在L0(x*)不存在任何点，从而P(x，x*)是不存在的。

定理5 设P(x，x*)是由式(3)定义的，且L0(x*)非空，若P(x，x*)=0，则x*是f(x)在 X上的其中一个全局极小点。

假若x*不是f(x)在X上的一个全局极小点，则至少存在一点*∈L0(x*)使得f*)＜f(x*)，即*∈L'(x*)。由定理3知P(x，x*)＜0。这与题设相矛盾。

定理6 设P(x，x*)是由式(3)定义的，则L0(x*)非空，若P(x，x*)=l＜0，则变换函数P(x，x*)在L0(x*)上存在一个极小点，有f()＜f(x*)。

定理6说明:只要变换函数P(x，x*)在原目标函数f(x)的当前极小点对应的严格水平集L'(x*)上取得非零的极小值，这时，变换函数的极小点就可以作为下一次原目标函数f(x)极小化过程的初始点。

3 无参数变换函数算法

基于以上对变换函数性质的讨论，给出无约束连续优化问题的一个无参数变换函数P(x，x*)的算法如下。

初始步:

(Ⅰ)选择δ=3，ε=10－8。

②心理干预:语言开导法,将患者所患的疾病向其作详细介绍,通过语言交谈,评估患者的心理情绪,并给予语言上的安慰、鼓励以及劝导等,纠正其错误的观念和思想,增强治疗信心。暗示法,根据患者的具体心理情绪,给予针对性的疏导和调适。可借助间接、含蓄法使得患者下意识接受治疗意见。劝导养生法,可采用传统中医养生法,例如宁神静志法、移情易性法以及情趣易性法等鼓励患者进行人际交往,多参加体育锻炼和机体活动。每天治疗20min,每周至少1次,共治疗4周。

(Ⅲ)令k:=0，表示迭代次数。

主步:

4 数值试验及分析

为了验证本文中提出的算法是可行和有效的，在计算机上用Matlab 7.0.1进行编程计算，将以下两个算例作为初步测试对象。

(Ⅰ)三驼峰函数

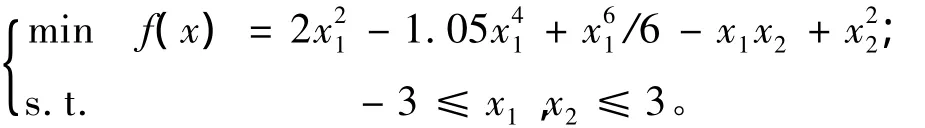
该问题的全局最小解和全局最小值分别是:x*=(0，0)和f*=0。

(Ⅱ)二维函数

其中c=0.20，0.50，0.05。对于所有的c，全局最小值都是f*=0。特别地，当c=0.20时，该问题的全局最小解是x*=(1.878 5，－0.345 8)。

现将计算结果列于表1和表2，表中的符号代表的意义分述如下:

k:迭代次数;

表1 算例(1)的计算结果

表2 算例(2)(c=0.20)的计算结果

由表1和表2可知:该算法是下降的，即能从当前局部极小点跳到下一个更好的局部极小点。因此，算法(Ⅰ)是可行和有效的。

5 结论

该算法充分利用了变换函数极小值的信息，即可以通过本文给出的算法的终止条件判定当前局部极小点是否是唯一全局极小点或其中一个相对全局极小点。并且随着容许误差εi的减小，通过执行算法得到的相对全局极小点列{x}和相对全局极小值列{f(x)}，进而判断出问题的绝对全局极小点x*和绝对极小值f(x*)。

［1］ Ge R P.A Filled Function Method for Finding a Global Minimizer of a Function of Several Variables［J］.Mathematical Programming，1990，46:191－204.

［2］ Ge R P.The Theory of Filled Function Methods for Finding Global Minimizers of Nonlinearly Constrained Minimization Problems［J］.Journal of Computational Mathematics，1987，5(1):1－9.

［3］ Ge R P，Qin Y F.A Class of Filled Functions for Finding a GlobalMinimizer of a Function of Several Variables［J］.Journal of Optimization Theory and Applications，1987，54(2):241－252.

［4］ Shang Y L，Pu D G，Jiang A P.Finding Global Minimizer with One-parameter Filled Function on Unconstrained Global Optimization［J］.Applied Mathematics and Computation，2007，191:176－182.

［5］ Shang Y L，Zhang L S.A Filled Function Method for Finding a Global Minimizer on Global Integer Optimization［J］.Journal of Computational and Applied Mathematics，2005，181(1):200－210.

［6］ YangY J，Shang Y L.A New Filled Function Method for Unconstrained Global Optimization［J］.Applied Mathematics and Computation，2006，173:501－512.

［7］ Zhang L S，Ng C，Li D，et al.A New Filled Function Method for Global Optimization［J］.Journal of Global Optimization，2004，28:17－43.

［8］ 尚有林，杨森，王三良.无约束全局优化的一个新凸填充函数［J］.河南科技大学学报:自然科学版，2004，25(4):78－81.

［9］ Cetin B C，Barhen J，Burdick JW.Terminal Repeller Unconstrained Suben-ergy Tunneling for Fast Global Optimization［J］.Journal of Optimization Theory and Applications，1993，77(1):97－125.

［10］ Levy A，Montalvo A.The Tunneling Algorithm for the Global Minimization of Functions［J］.SIAM Journal of Scientific and Statistical Computing，1985，6(1):15－29.

［11］ Yao Y.Dynamic Tunneling Algorithm for Global Optimization［J］.IEEE Transactions on Systems，Man and Cybernetics，1989，19(5):1222－1230.

［12］ Chew SH，Zheng Q.Integral Global Opyimization:Lecture Note in Economics and Mathematical Systems［M］.Berlin: Springer-Verlag，1988.

［13］ 郑权，将百川，庄松林，等.一个求总极值的方法［J］.应用数学学报，1978，1(2):161－174.

［14］ Stanley O，James A S.Fronts Propagating with Curvature-dependent Speed:Algorithms Based on Hamilton-Jacobi Formulations［J］.Journal of Computational Physics，1988，79(1):12－49.