分子结合的物理本质探究

刘建科， 解 晨， 杨若欣， 李 洋

(1.陕西科技大学 理学院，陕西 西安 710021; 2.陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

0 引言

粒子之间是通过范德瓦尔斯力结合在一起的.但不同粒子之间范德瓦尔斯力的成因又不尽相同.离子晶体的结合是由于相异离子之间库仑力的存在而结合，而分子是中性的，分子晶体中分子之间是靠什么力结合在一起的?对这个问题，在历史上并不是一下子就认识清楚的，而是经历了一段认识的发展过程.1912年葛生(Keesom)研究了极性分子之间的相互作用，1921年德拜(Debye)研究了极性分子与非极性分子之间的相互作用，1930年伦敦(London)研究了非极性分子，例如惰性原子之间的相互作用.这3种力分别称为葛生力、德拜力和伦敦力[1].文中特别给出了这3种力的相对大小，这对理解晶体的结合具有重要意义.在其他文献中未见相关而全面的报道[2].

1 静电力(葛生力Keesom)

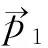
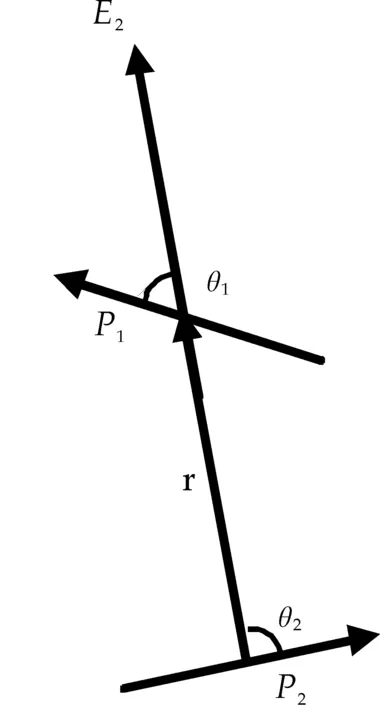
图1 两个偶极矩之间的相互作用

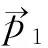
(1)

故最后得

2 诱导力(德拜力Debye)

极性分子与非极性分子之间也有作用力，因为非极性分子可以被极性分子的电场极化而产生诱导偶极矩，故它们之间的作用称为感生相互作用.一个分子的电荷分布要受其它分子电场的影响，故二者之间存在诱导力.第一分子受到第二分子电场E2的作用，要产生诱导偶极矩μ1=ex1=α1E2；同样，第二分子受到第一分子电场E1的作用，要产生诱导偶极矩μ2=α2E1.其中α1,α2分别为第一、第二两分子的极化系数.E2作用于第一分子，使其畸变，畸变能为

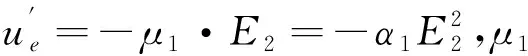
取平均后用(1)式，得

对第二分子被第一分子极化的情形，同样有

两者的总和为

对于具有偶极矩的分子，考虑到它们的相互极化时，其总的相互作用能应为

u=uk+uD

(2)

对于同类分子，α1=α2=α，p1=p2=p，则

(3)

3 色散力(伦敦力London)

惰性气体分子的电子云分布是球形对称的，偶极矩p等于零，按(3)式，它们之间的相互作用能u应等于零.但实验结果证明它们之间仍然有相互作用力存在.因此，除了前两种力以外，分子之间一定还有第三种力，1930年伦敦用瞬时偶极矩的相互作用并结合量子力学证明了这种力的存在，称为色散力或伦敦力，其间为色散相互作用.下面只用一种简单的模型来说明这种力的产生.

为简单起见，用带电粒子的线性谐振子代表瞬时偶极矩.如图2所示，r为两个谐振子平衡点(正电荷所处的位置)之间的距离，x1与x2为带负电荷的质点在振动过程中离开平衡点的瞬时位移.这两个振子的能量分别为

图2 两个瞬时偶极矩的相互作用

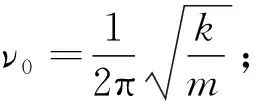
当r≫x1、x2时，上式可以展开并只取第一项而略去高次小的项，则系统的总能量可以写为

E=E1+E2+u12

由于电场E的作用，使振子产生一位移x，且eE=kx，k为恢复力常数.产生的瞬时偶极矩ex=αE，α为极化系数.由此可得kα=e2，代入上式并引入新坐标

可得

可见，引入新坐标后，系统的能量可以表示为两个独立振子的能量之和，系统的力常数分别为k1与k2，振动频率分别为

为简单起见，我们只讨论两个振子均在基态(n=0)，E取零点能的情形.可以看出：

(2)两振子有相互作用时，系统的能量为

一般可以把2α/r3看成微小的量，展开上式，舍去高次项，上式可展开成

(4)

根据(2)、(4)式的讨论，可知分子之间总的相互作用能等于

u=uK+uD+uL

对相同的分子，则有

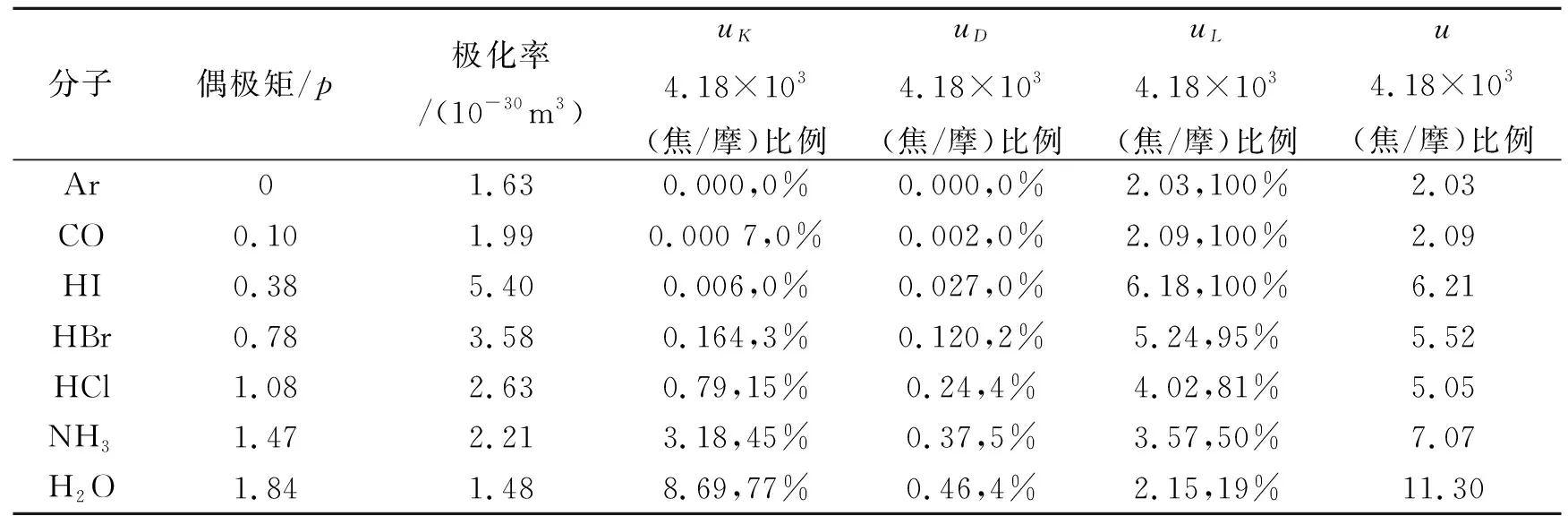
表1 范德瓦耳斯力的分配[3，4]

4 结论

对不同的分子，总起来说，p,α,v的数值不同，利用上式可以分别计算出[3,5,6]uK,uD,uL.这3种力共同具有如下的特性：(1)这是普遍存在于分子或原子之间的一种力，即使它们的偶极矩p等于零，亦还存在色散力；(2)它是吸引力，与r-7成正比，作用范围约有零点几个纳米；(3)与共价键不同，它一般是没有方向性和饱和性的；(4)在不同分子中，uK、uD和uL3种作用所占的比例是不同的，一般色散力所占的比例较大，见表1中所列的数据；(5)这3种力统称范德瓦耳斯力.

[1] 苟清泉.固体物理学简明教程[M].北京：人民教育出版社，1978.

[2] B.M.Axlrod,E.Teller,J.Chem.Phys.1943,22:1 619.

[3] Eisenschitz,London,Zeit,fürphysic,1930,60:4 917.

[4] 冯 端.固体物理学大辞典[M].北京：高等教育出版社，1998.

[5] 刘建科.强噪声下检测微弱信号的新方法[J].物理学报，2000，50(11)：2 185-2 191.

[6] 刘建科,刘彩云.原子谱线增宽的解释[J].光谱学与光谱分析，2003,23(3):605-606.