基于冲击因子的两个装药延时起爆目标毁伤评估方法研究

胡俊波，张志华，李庆民

(海军工程大学 兵器工程系，武汉 430033)

自第二次世界大战以来，人们对水下爆炸进行了比较系统的研究，当时主要是从军事角度着重分析水下爆炸现象及水下爆炸对舰船的破坏效应。其开创性工作以Cole于1948年出版的《水下爆炸》为代表，它总结了当时有关水下爆炸的试验及理论研究的主要成果，介绍了水下爆炸的现象、水下爆炸载荷传播及分布特点、水下爆炸的试验研究方法及水下爆炸载荷测试技术，并从理论上探讨了水下爆炸机理，现今人们仍然在广泛使用Cole的计算公式［1］。

同时，实践表明，两个或多个装药同时引爆可使作用区域内压力显著增强，对于提高炸药破坏威力十分有利，无论在军事还是国民经济建设领域，两个或多个装药同时引爆的应用越来越广泛［2-4］。姚熊亮等［5］研究比较了单发命中和多发武器同时命中潜艇冲击环境的异同，对于整个潜艇的生命力研究有着重要的意义。但是，国内外关于两个装药同时引爆冲击载荷计算方法的研究很少，Cole的计算公式又不适用于两个装药的情形，从而使得水下目标毁伤效果的评估工作不能有效开展。

本文给出了两个装药采用普通电雷管进行引爆，起爆时间存在一定延迟时冲击载荷的计算方法，研究了水下目标毁伤效果的评估方法。最后的试验结果表明，冲击载荷计算方法正确，毁伤评估方法能较好的反映目标的毁伤情况。

1 两个装药延时起爆冲击载荷计算

1.1 基本假设

为了简化问题，作如下假设:

(1)Cole的经验公式对于单个装药成立(正确);

(2)两个装药被布置在相同水深处，与目标的中剖面在同一平面内;

(3)装药为球形TNT装药;

(4)引爆两个装药时，由于普通电雷管性能的制约，两个装药的起爆时间存在一定的延迟，使得两个装药的爆炸冲击波不会发生碰撞。当使用普通电雷管同时引爆装药时，其延迟一般在10 ms(见表2)左右，设冲击波在水中传播的速度为v，两个装药的延迟为ΔT，那么当两个装药的距离小于10 m时有v·ΔT＞10 m，假设条件4是合理的。

这时，当第一个装药爆炸后，随着爆炸冲击波的传播，冲击波能量逐渐散逸到水中并形成一个具有一定压力、较高密度和温度的流场［6］，第二个装药爆炸产生的冲击波在这样的流场中传播，其散逸到水中的能量比在静水中传播时少，冲击波超压明显增大。本节主要研究第一个装药散逸能量的分布，第二个装药散逸能量的减少及冲击波超压的计算。

1.2 冲击波散逸能量分布的拟合

冲击波推进时，由于波阵面的压力和速度远高于波头前，冲击波能量散逸到水中，这种冲击波能量的散逸在装药附近时最急剧。由于装药附近冲击波超压过高，因此这个区域内的试验测量是较为困难的，Cole给出了冲击波能量的理论计算结果如表1所示，并指出“可以认为，计算水下爆炸时能量的分布具有令人满意的方法［7］”。

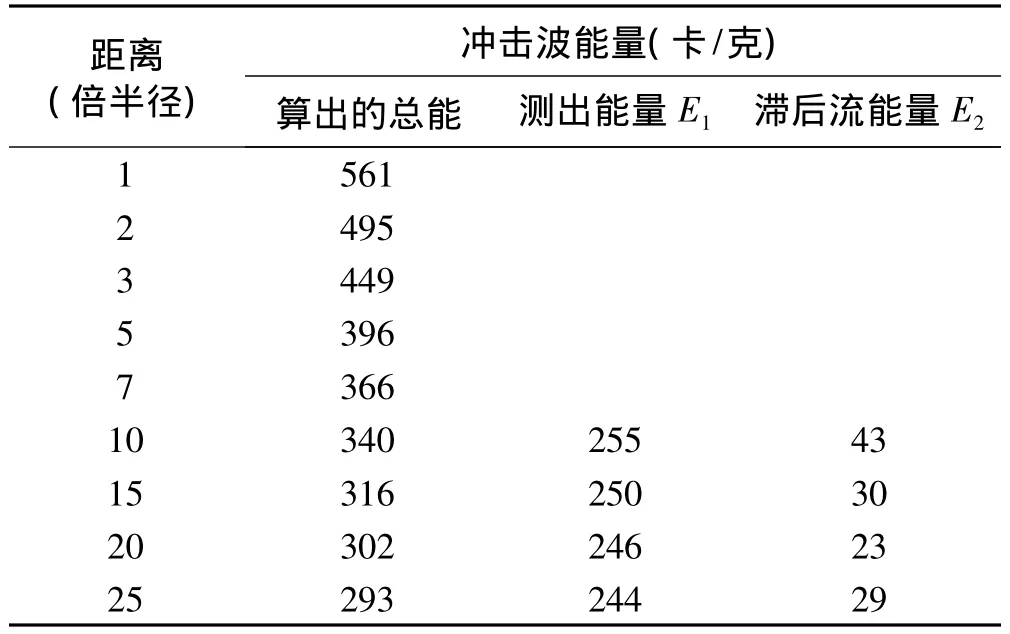
表1 TNT水下爆炸时的散逸能量Tab.1 Emission energy of underwater explosion by using TNT

从表1中可以看出，冲击波携带的能量随波头的推进而迅速减小。约25%的冲击波初始能量散逸在半径等于五个药包半径的体积内，约50%散逸在半径等于25个药包半径的体积内。利用表1中的数据，拟合可以得到冲击波散逸能量关于倍半径的解析表达式，这样就能够方便的计算装药平面内各点处的散逸能量及散逸能量密度。在拟合散逸能量分布时，采用指数模型进行拟合，结果如下:

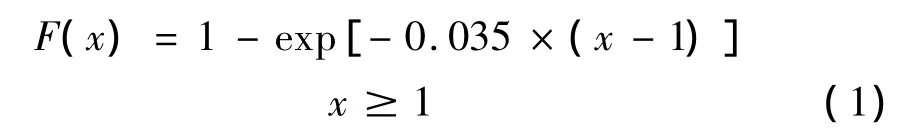
其中，F(x)为散逸能量与初始冲击波能量的比值;x=R/R0为倍半径;R0为装药的半径，拟合效果如图1所示。

1.3 冲击载荷计算

因为第一个装药爆炸后，其冲击载荷是在静水中传播的，所以冲击载荷传播到某一观测点时的冲击波超压可通过Cole的经验公式求得。对于第二个装药，计算其冲击波超压需要利用拟合得到第一个装药冲击波散逸能量的分布，计算其散逸能量密度，在考虑散逸能量衰减系数和被第二个装药利用的比例系数后，可求得第二个装药传播到某一观测点时其散逸能量较静水中的减少量。散逸能量的减少意味着冲击波能量的增强，而冲击波能量与冲击波超压的平方成正比关系，依据这一关系，可求得第二个装药冲击载荷传播到某一观测点时的冲击波超压。

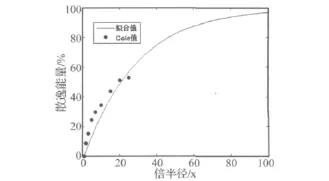
图1 冲击波散逸能量分布拟合图Fig.1 Distribution fitting of shock wave’s energy emission

无限水域中单个球形TNT装药的冲击波超压计算方法大都由Cole的经验公式衍生而来，现今使用较多的是［8-9］:

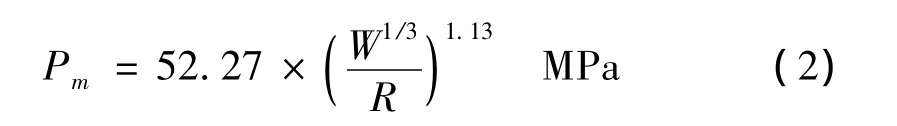
其中W为装药量(kg)，R为爆距(m)。

式(2)用于计算无限水域中单个球形TNT装药的冲击波超压被认为是较准确的，但该公式不适用于两个装药延时起爆的情形。两个装药爆炸的示意图如图2所示，其中O1为第一个装药的爆炸点，O2为第二个装药的爆炸点，M为观测点。同时引爆两个装药时，存在一定的延迟T，使得第二个装药开始爆轰时第一个装药的冲击波已经传播到了S点，A为O2M上任意一点，不妨设:

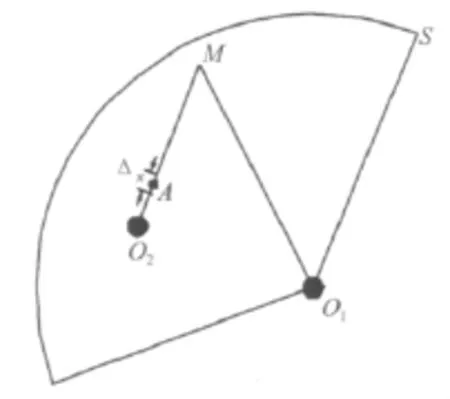
图2 两个装药与观测点位置示意图Fig.2 Schematic of two charges and observation location

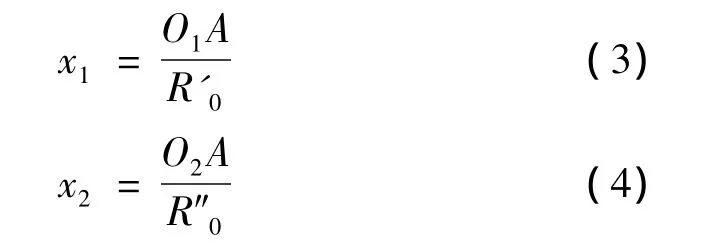
R'0，R″0分别为第一、二个装药的半径。

拟合第一个装药散逸能量的分布后，引入散逸能量衰减系数和被第二个装药利用的比例系数后，可求得第二个装药传播到某一观测点时冲击波能量的增加量，两个装药冲击波超压的计算公式为:

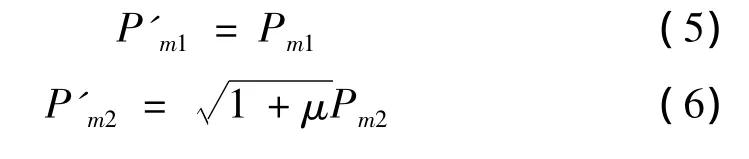
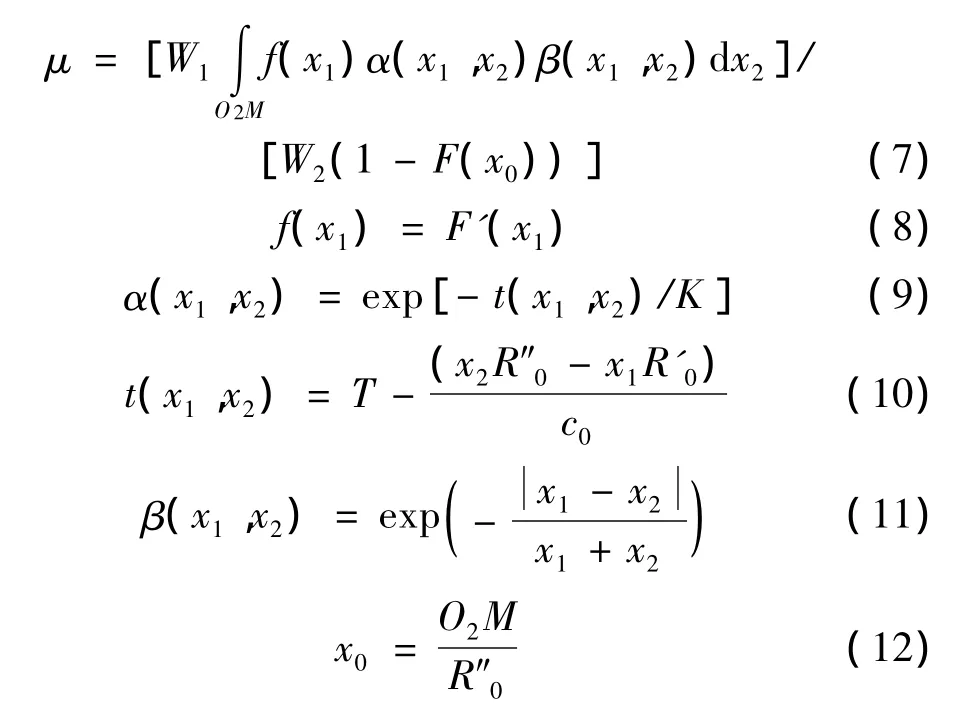
其中，Pm1，Pm2为利用式(2)计算得到的观测点M处第一、二个装药的冲击波超压;P'm1，P'm2为本文给出的两个装药分别在观测点M处的冲击波超压;μ为第二个装药的冲击波传播到观测点M处时，冲击波能量较静水中传播时增大的幅度;W1、W2分别为两个装药的装药量(kg);f(x1)为第一个装药在A点处的散逸能量密度;K是散逸能量衰减到1/e时的时间常数，其值越大，散逸能量衰减得越慢，其值越小，散逸能量衰减得越快;α(x1，x2)为两个装药冲击波到达A点的时间差引起的A点处散逸能量的衰减，由于A点附近的温度和速度是连续的，不像冲击波一样存在突变，而两个冲击波到达A点的时间差一般较小，可以取α(x1，x2)≈1;β(x1，x2)为散逸在A点处的能量被第二个装药利用的比例系数，在这里认为两个装药在A点处的冲击波能量差异较小时，比例系数较高，反之，则较小。

2 水下目标毁伤评估方法

2.1 新型冲击因子

为了描述水下爆炸对目标的毁伤效果，人们引入了冲击因子的概念，但是究竟选用何种冲击因子最具有代表性，目前世界各国有不同的看法，还没有形成统一的标准。常用的冲击因子有两种形式，一种是基于冲击波超压的冲击因子，这种冲击因子的定义为:

另一种是基于目标遮挡的冲击波能量的冲击因子，这种冲击因子的形式为:

上个世纪80年代，北约各国海军认为:仅以冲击波超压为标准，不符合实际情况，因此提出了如式(14)所描述的标准。这种形式的冲击因子是基于平面波假定的，若爆距R与目标结构特征尺度L相比足够大［10］，这一计算方法是较为合理的。但实际情况并不总是这样，于是姚熊亮等定义了新型的球面波水下爆炸冲击因子［10］Cm为:

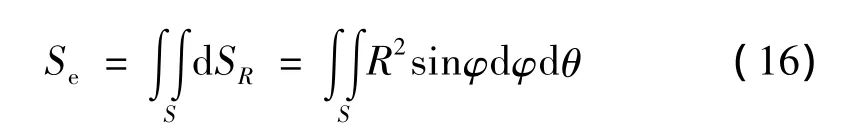
其中Se为目标在以爆炸点为球心的某一球面上的投影面积。计算时，通常取以爆距R为半径的球面。但这一方法仍然存在一定的不足:没有考虑传播到目标不同部分的冲击波在能量上的差异，也即该方法认为传播到目标各部分的冲击波能量密度是相同的。为此，作者在文献［11］中提出了一种改进的新型冲击因子:

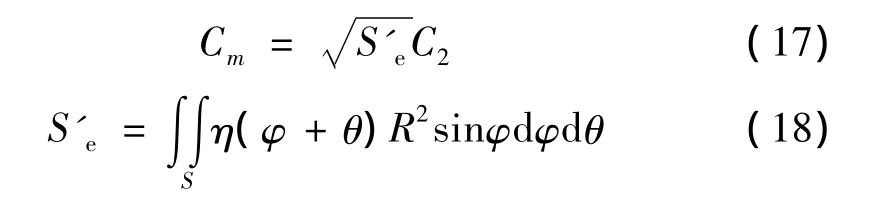
其中η(φ+θ)为目标积分曲面内任意一点的冲击波能量与爆距R处冲击波能量的比值［11］。

2.2 两个装药延时起爆水下目标毁伤评估方法

利用本节引入的新型冲击因子，可以通过单个装药水下爆炸毁伤目标的试验数据估计出使得水下目标毁伤的冲击因子临界值及其方差，并计算目标的毁伤距离曲线，该评估方法取得了较好的效果［11］。

对于两个装药延时起爆水下目标毁伤效果的评估，仍然考虑采用新型冲击因子进行度量。不同的是两个装药延时起爆其冲击因子由两部分组成，第一个爆炸装药的冲击因子可依据式(17)、式(18)计算得到，而由于第二个爆炸装药的冲击载荷发生了变化，因此需对第二个装药的冲击因子值进行修正。其修正的基本思路是:由于两个装药延时爆炸，第二个装药的冲击波传播到目标处时，冲击波能量较静水中传播时增大的幅度为μ'(关于μ'的计算见1.3节中的式(6)～式(12))，而新型冲击因子是基于目标遮挡的球面冲击波能量，所以引入了修正项(1+μ')。两个装药延时起爆冲击因子的计算方法如下:

其中，CA是两个装药延时起爆的冲击因子;W1、W2分别为两个装药的装药量(kg);R1、R2分别为两个装药的爆距(m);μ'为第二个装药的冲击波传播到目标处时，冲击波能量较静水中传播时增大的幅度。

3 试验结果及评估分析

为了验证冲击载荷计算方法的合理性并估计出毁伤目标的冲击因子临界值，在702所水下爆炸试验池进行了两个装药延时起爆的水下目标抗爆炸试验。该水池是目前国内唯一的大型水下爆炸试验水池，水池水面直径85 m，池底直径10 m，水深15 m，呈倒圆台型。试验中使用的装药均为1 kg球形TNT装药，用普通电雷管引爆，共进行了三次试验，装药与目标的相对位置如图3所示。在两个装药非目标所在侧，布置了压力传感器用以测量冲击载荷，在观测点测得的#1试验压力时间曲线如图4所示。压力传感器采用的是美国的PCB-138A50，测量误差为5%。进行的三次试验，分别按照Cole和本文提出的方法计算得到了观测点处的冲击波超压。试验条件、计算及测量结果如表2所示。从表2可以看出，按照本文提出的两个装药延时起爆时冲击载荷的计算方法得到的结果与试验结果一致性较好，明显好于采用Cole经验公式得到的结果，表明该计算方法是正确合理的。

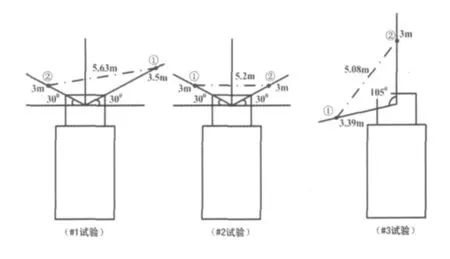
图3 两个装药延时起爆试验方案Fig.3 Test scheme of two simultaneous blasts

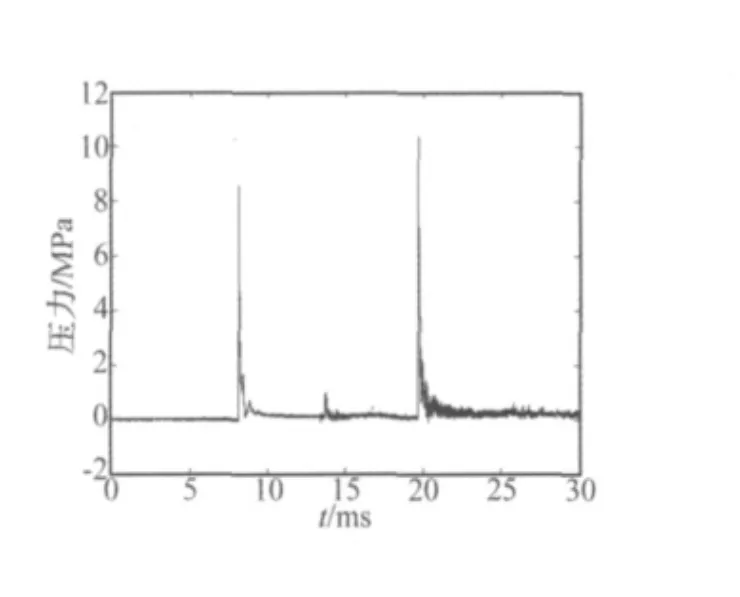
图4 #1试验观测点处的压力时间曲线Fig.4 Pressure-Time curve of observation location of#1 test

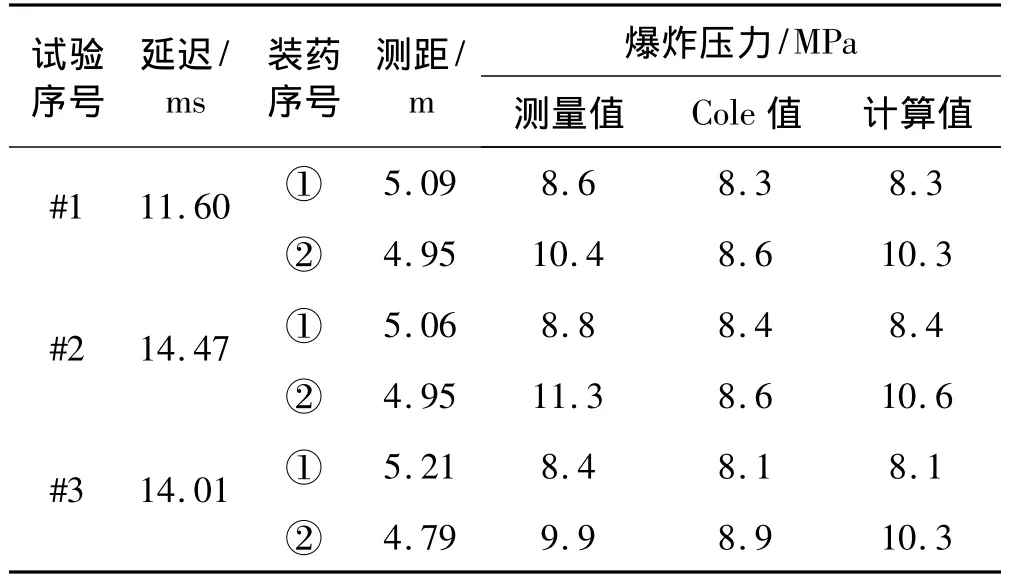
表2 两个装药延时起爆冲击波超压测量与计算结果Tab.2 Test and computation result of peak pressure of two charges’shock wave

进行抗水下爆炸试验的水下目标由两部分组成:易损部分和耐炸部分。耐炸部分的有效损伤距离较小(＜1 m)，试验中毁伤的都是易损部分，因此在计算作用在目标上的能量时只考虑了直接作用在目标易损部分上的能量，而直接作用在耐炸部分又传递到易损部分的能量则未做考虑。易损部分长度L=380 mm，圆柱半径r=210 mm，按照第二节中提出的两个装药延时起爆冲击因子的计算方法，可以得到不同试验工况下的冲击因子如表3所示。

从表中数据可以看出，使得目标毁伤的工况其冲击因子的值分别为0.291 6、0.314 9，而目标未毁伤的工况其冲击因子的值为0.277 0，冲击因子的大小与目标的毁伤情况表现了较好的一致性，从而表明该冲击因子能较好的反映目标的毁伤情况。

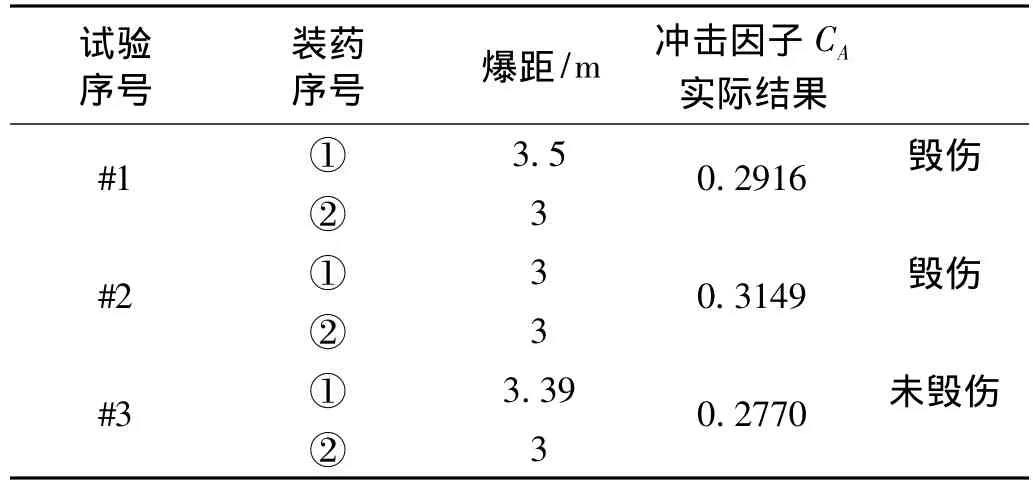
表3 不同试验工况下的冲击因子Tab.3 Impulsive factor in different case

由于试验数据不足，无法精确估计出目标毁伤时冲击因子的临界值。简单起见，取临界值CA0为#1试验和#3试验冲击因子的均值，即:

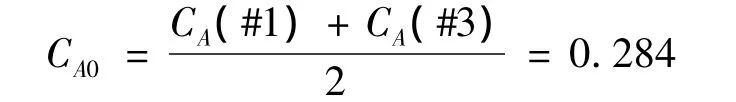
利用该临界值，可以对各种工况下两个装药延时起爆时水下目标的毁伤情况进行评估。其思路是:首先，依据式(19)-式(23)给出的方法计算某一工况的冲击因子，然后将冲击因子值与临界值比较就可以对水下目标的毁伤情况进行评估。

4 结论

为了对两个装药延时起爆情况下水下目标的毁伤效果进行评估，本文在在拟合冲击波散逸能量的分布的基础上，利用散逸能量密度、衰减系数等，给出了两个装药延时起爆时冲击载荷的计算方法。通过引入一种新型冲击因子，给出了两个装药延时起爆情况下目标毁伤效果的评估方法，最后的试验结果表明，冲击载荷计算方法正确，毁伤评估方法能较好的反映目标的毁伤情况。

虽然给出了两个装药延时起爆情况下目标的毁伤评估方法，但也存在一些不足，主要表现在两个装药延时起爆的试验开展得不够充分，使得目标毁伤时冲击因子临界值的估计过于简单，这有待于在以后研究工作中进一步完善。

［1］尹 群，陈永念，胡海岩.水下爆炸研究的现状和趋势［J］.造船技术，2003:(6):6-12.

［2］孙百连，顾文彬，蒋建平，等.浅层水中沉底的两个装药爆炸的数值模拟研究［J］.爆炸与冲击，2003，23(5):460-465.

［3］张明晓，张 立，王神送.双药包水下爆炸相互作用研究［J］.煤矿爆破，2008(4):5-8.

［4］李旭东，刘凯欣，张光升，等.冲击波在水泥砂浆板中的聚集效应［J］.清华大学学报(自然科学版)，2008，48(8):1272-1275.

［5］姚熊亮，许维军.多发武器同时命中时潜艇冲击环境研究［J］.船舶工程，2004，26(5):42-49.

［6］鲍 姆.爆炸物理学［M］.北京:科学出版社，1964.

［7］库尔.水下爆炸［M］.北京:国防工业出版社，1960.

［8］牟金磊，朱 锡，张振华，等.水下爆炸载荷作用下加筋板的毁伤模式［J］.爆炸与冲击，2009，29(5):457-462.

［9］陈海龙，姚熊亮，祁 磊，等.舱壁结构在水下爆炸中的动态稳定性研究［J］.振动与冲击，2009，28(3):14-17.

［10］姚熊亮，曹 宇，郭 君，等.一种用于水面舰船的水下爆炸冲击因子［J］.哈尔滨工程大学学报，2007，28(5):501-509.

［11］胡俊波，张志华，李庆民.水下爆炸对水下目标的毁伤评估研究［J］.振动与冲击，2010，29(10):216-220.