动力总成悬置系统频率和解耦率的稳健优化方法

吴 杰，周胜男

(1.华南理工大学 机械与汽车工程学院，广州 510641;2.广东省汽车工程重点实验室，广州 510641)

改善动力总成悬置系统的性能，既可以降低动力总成本身的振动，又能降低其传递到车架或车身上的反力以及车内噪声。目前，国内外研究者主要采用确定性方法对悬置系统进行分析和设计［1-3］，即假定悬置系统参数(例如，悬置刚度和安装位置等)为确定值。但是，在悬置的制造、安装和使用过程中，悬置刚度不可避免地存在一定程度的偏差或波动。进行动力总成刚体振动模态的频率配置和解耦布置是动力总成悬置系统设计的基本任务［1，3］，频率和解耦率的计算方法详见文献［3］。当悬置刚度存在不确定性时，在设计阶段准确预测悬置系统固有频率和解耦率的变化特征，对分析和提高悬置系统性能的稳健性有重要意义。

基于试验设计方法，Qatu［4］计算分析了悬置刚度的变化对动力总成悬置系统频率配置的影响;Sirafi和Chang［5］仿真研究了橡胶悬置刚度和副车架刚度的变化对悬置系统解耦率的影响;翁建生等［6］考虑了悬置系统的稳健性要求，提出了悬置系统模糊多目标优化方法;吴杰等［7］将悬置刚度、安装位置和角度当作正态随机变量，对悬置系统的解耦率进行了稳健性优化设计。尽管通过实验可以近似得到一些不确定参数的统计特性，但Ben-Haim［8］指出:小的随机参数统计特性误差会造成较大的系统稳健性分析偏差。与得到不确定参数真实的统计特性相比，获得不确定参数的变化范围通常比较容易［9-10］。Jiang 等［12］把结构载荷、弹性模量或泊松比等非设计参数当作区间参数，提出了一种区间规划方法，但没有考虑最优设计变量的波动问题。

文中采用区间数描述悬置刚度变化的不确定性。提出了计算悬置系统固有频率和解耦率变化范围的改进区间截断方法。考虑到最优设计变量的波动问题，提出了区间型稳健优化方法，对悬置系统的解耦率和频率进行了稳健性优化。

1 频率和解耦率的区间分析方法

1.1 计算函数值精确变化区间的组合方法

区间分析方法有广泛的工程实际背景。例如，在结构设计中，零件的尺寸要求为x(名义值)，容差为±Δx，则加工出来的零件实际尺寸必然在［x-Δx，x+Δx］范围内变化，称x为区间参数，Δx称为区间参数的半径。

若区间值函数f(，，…，)是每个区间变量的单调函数，则函数的精确变化区间可以由其在所有区间变量左右端点处的组合而计算得到［11］。

令=［，］=［)，］，i=1，2，…，n，则当区间变量取端点值时，f的所有可能取值为:

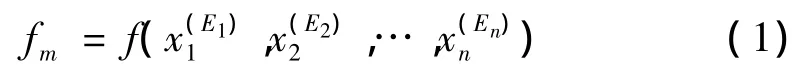
其中，Ei=L，R，i=1，2，…，n，m=1，2，…，2n。

函数f的精确变化区间为:

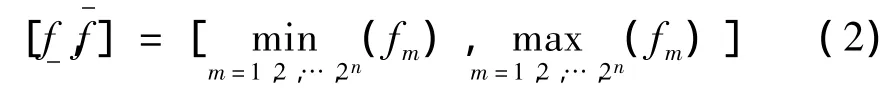
通过灵敏度分析可知，当悬置刚度在其名义值附近波动±1%～±5%时，悬置系统的六阶固有频率和各方向解耦率均为各悬置刚度参数的单调函数。因此，可以采用组合方法求得固有频率和解耦率的精确变化范围。当变量较多时，组合方法的计算效率较低。

1.2 计算函数值近似变化区间的区间截断方法

当 Δ1≤t，Δ2≤t时，

当 Δ1＞t，Δ2＞t时，

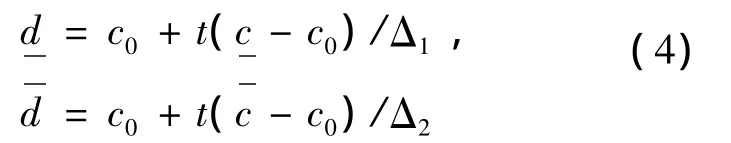
当 Δ1≤t，Δ2＞t时，

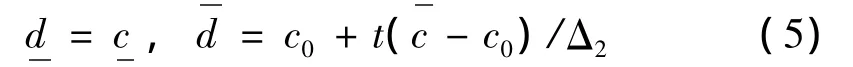
当 Δ1＞t，Δ2≤t时，

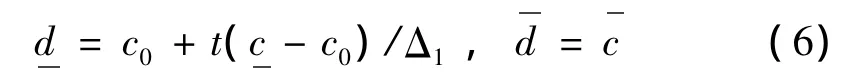
然而，上述方法毕竟是建立在假设“允许的函数近似区间值的最大相对偏差为2t”之上的。当函数精确区间值的相对不确定量与t接近时，文献［11］中t的取值方法是正确的，例如文献［11］的10杆结构中，当各杆的截面积有±1%的误差时(此时t=δmax=0.01)，各杆应力的精确区间值的相对不确定量均在0.01附近波动，计算精度很高。

但很多实际问题中，函数精确区间值的相对不确定量可能远大于t(与t不在一个数量级)，此时文献［11］中的t的取值方法将失效。对动力总成悬置系统而言，当悬置刚度在其各自区间内变化时，某些方向解耦率的变化区间的相对不确定量远大于悬置刚度变化的百分比(即相对不确定量δ)，因此，必须改进文献［11］中t的取值方法。

假设各悬置刚度参数变化区间的相对不确定量均为δ，δ取值为1%～5%。在此，针对频率和解耦率给出不同的t值取值方法:

(1)动力总成悬置系统各频率区间值的相对不确定量与t相差不大，仍采用区间截断式(3)至式(6)进行预估区间值的修正，为提高计算精度，取t=δ/2;

(2)由于某些方向上解耦率区间值的相对不确定量远大于t，因此，用k(t)(t的某种函数)取代t。计算解耦率变化区间时，针对不同的悬置刚度变化百分比，用最小二乘法得到k(t)的最佳取值:

当 Δ1≤t，Δ2≤t时，

当 Δ1＞t，Δ2＞t时，

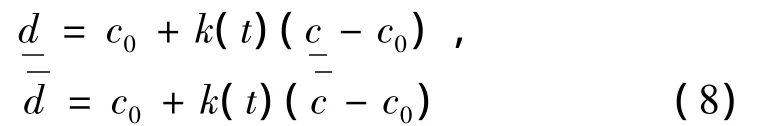
当 Δ1≤t，Δ2＞t时，

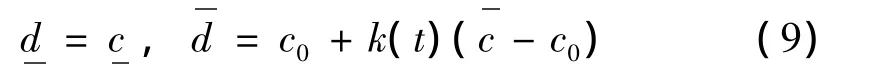
当 Δ1＞t，Δ2≤t时，

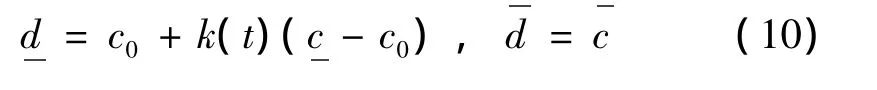
其中，k(t)为t的函数，t=δ。

当k(t)取不同形式的函数时，采用最小二乘法拟合近似区间值和精确区间值，可以发现，当k(t)为有理分式，并且分子和分母分别为t的一次函数和二次函数时，即k(t)=(k0t+k1)/(t2+k2t+k3)时，拟合效果最好。根据悬置系统的初始刚度，图1给出了k(t)的拟合效果，拟合得到的参数为:k0=-0.001 693，k1=0.010 27，k2=0.000 481 8，k3=-2.369E-6。

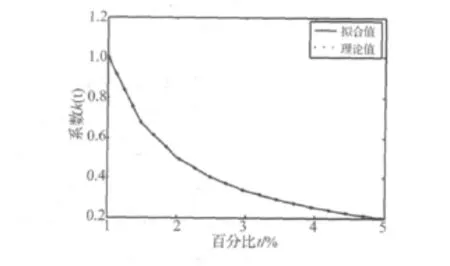
图1 k(t)的拟合效果Fig.1 Fitting result of k(t)

2 解耦率的区间可靠度

假设解耦率的近似区间值用［，］表示，其要求的安全变化区间值用［，］表示，在数据不全的情况下，一般假设解耦率是均匀分布在区间［，］上的。从物理意义上理解，若［］与［］有交叉，则该悬置系统在一定程度上可以满足各方向解耦率的变化区间的要求，用R度量这种“满足程度”，用1-R度量“不满足程度”，并定义R为区间可靠度。

当［，］完全属于［］时，R=1;当［，］完全位于［］之外时，R=0;当［，xE］与［，］有交叉时，按下式计算R［11］:

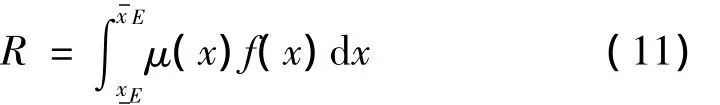
3 频率的区间概率度

当悬置刚度为区间参数时，悬置系统频率必然有一定的变化区间，在此，用区间概率度来度量频率约束条件的满足程度。区间概率度表征一个区间数大于另一个区间数的“程度”。

定义区间概率度［12］:

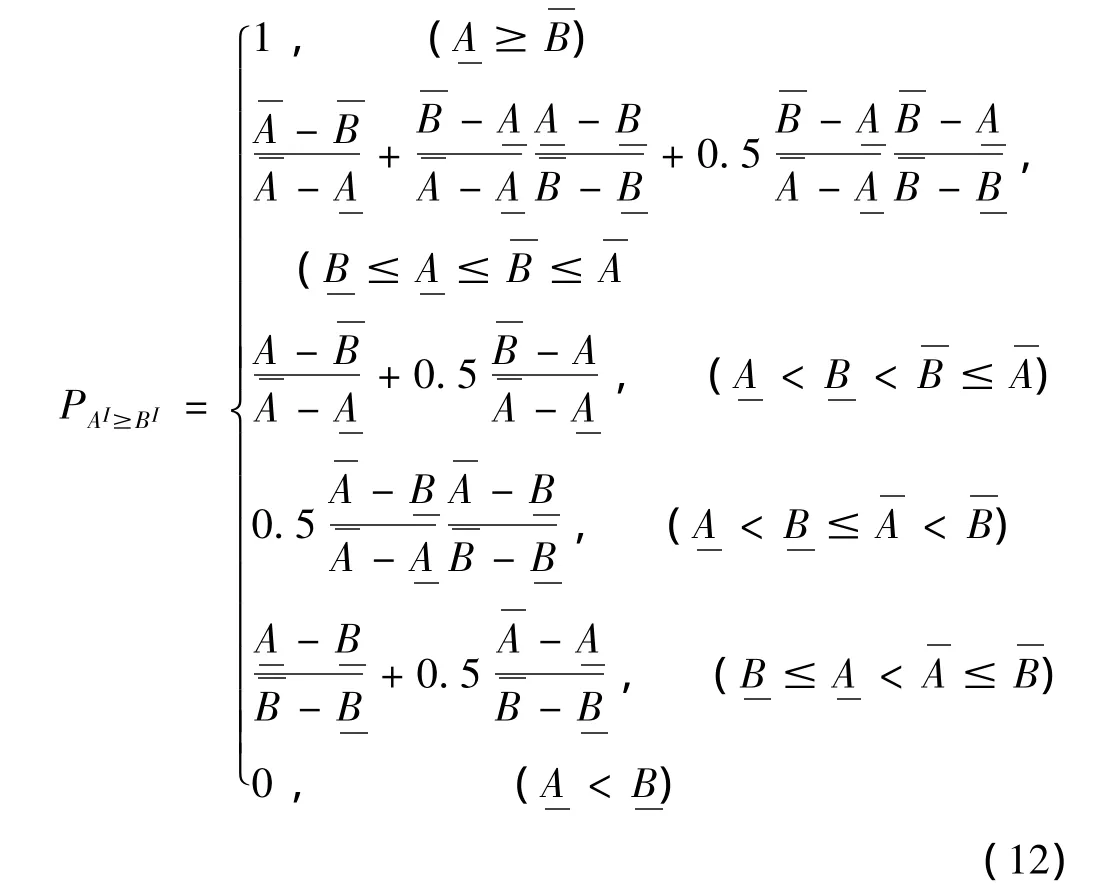
由式(12)可知，0≤PAI≤BI≤1。例如，设第i个约束条件为≤gi(xI)≤，写成概率度约束条件为≥α_R，且≥α_L，其中，和分别是第i个频率约束的上、下界;α_L和α_R分别为满足约束条件i的指定的左、右区间概率度。

4 频率和解耦率的区间优化模型

发动机在整车中的安装位置限制较严格，一般不改变悬置的安装位置和角度。因此选择四个悬置的刚度为优化设计参数。

假设刚度的不确定性由其名义值变化±1%～±5%表征，具体数值与制造工艺水平及使用工况有关。为了使悬置系统的频率和解耦率更加稳健，在优化设计时，应综合考虑各种不确定因素对优化结果可能产生的影响。为此提出区间优化方法，考虑最优设计参数发生波动时进行稳健优化设计，而不仅仅是考虑非设计参数的不确定性［12］。

提出悬置系统解耦率的区间优化模型为:

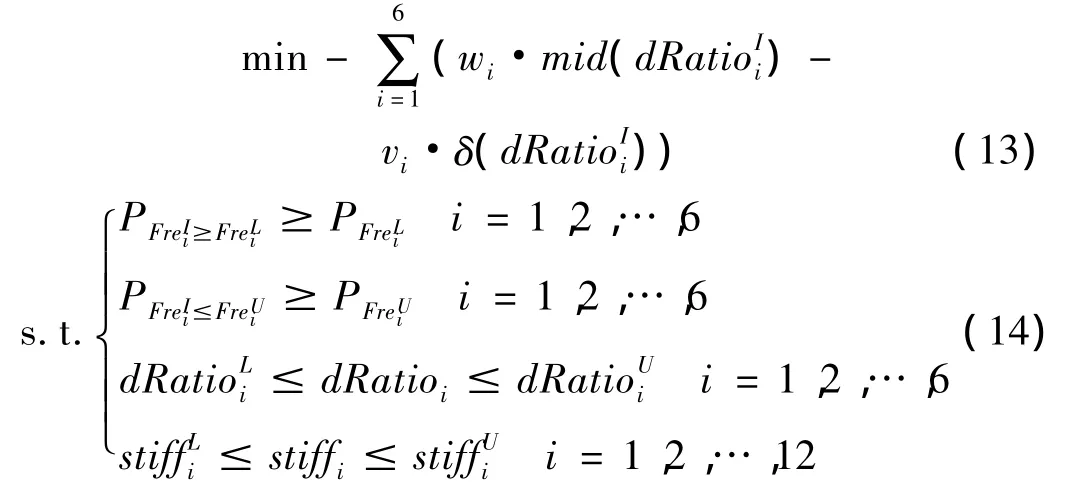
其中，当刚度参数在其名义值附近波动时，为各解耦率的变化范围，和分别为dRatio的左、右约束界限，mid()和δ()分别为的中点和相对不确定量，wi和vi为权重;Frei(i=1，2，…，6)是悬置系统的6个固有频率，是各固有频率的变化区间，和和分别为Frei的左、右约束界限;6个固有频率的约束界限分别为:6 ～12 Hz，6 ～12 Hz，8 ～10 Hz，6 ～15 Hz，9 ～11 Hz和6～15 Hz;和(i=1，2，…，6)分别表示给定的满足约束条件i的左、右区间概率度;stiffi(i=1，…，12)是刚度设计变量和分别为stiff的左、右约束界限，此处假设stiffi可以在其初值附近变化±25%。

为方便对比，下面给出确定性优化模型:

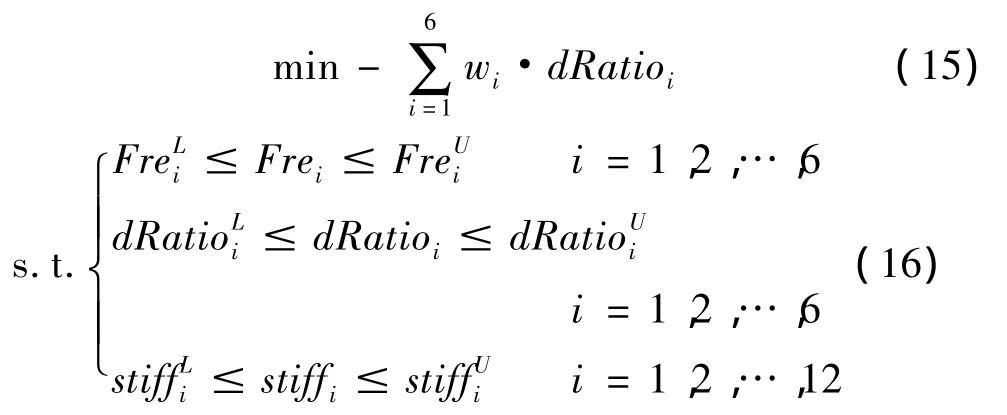
可以看出，区间优化模型不但要使悬置系统在各个方向具有尽量高的解耦率，并且当最优刚度参数发生波动时，还要保证解耦率变化区间的半径最小，使得各解耦率尽可能的稳健。而确定性优化方法只能保证得到各方向最大的解耦率，当最优刚度参数发生波动时，不能保证解耦率的稳健性。

在区间优化迭代过程中，每得到一组设计参数值，便假设该组设计参数在其名义值附件发生一定程度的波动(±1%～±5%)，利用提出的改进区间截断方法进行频率和解耦率的区间分析，进而计算优化目标值和约束条件值。当然，由于每次迭代时刚度参数的不同，区间截断方法中的k(t)也不同。文中尝试在每次优化迭代时，使用由初始刚度参数经最小二乘法拟合得到的k(t)中的最优系数。虽然每次迭代中由该组系数计算的解耦率的近似区间值与精确区间值有一定偏差，但由式(13)可以看出，优化目标是使得解耦率的名义值最大以及解耦率区间值的宽度最小。因此，优化迭代的搜索方向受每次迭代时解耦率区间值的计算精度的影响很小，可以忽略不计。

5 算例

图2为具有4个悬置的某轿车横置动力总成悬置系统。

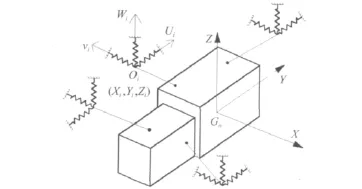
图2 动力总成悬置系统的六自由度模型Fig.2 6DOF model of a powertrain mounting system

动力总成坐标系G0-XYZ的原点G0位于动力总成质心，Y轴平行于发动机曲轴轴线方向并指向发动机前端，X轴水平指向汽车后方，Z轴垂直曲轴向上。每个悬置简化成沿其三个弹性主轴方向具有刚度和阻尼的元件［1，3］，悬置的三个弹性主轴分别用ui，vi和wi表示(i=1，2，…，n，n为悬置个数)。动力总成重量为 215 kg，表1给出了动力总成的转动惯量和惯性积，表2给出了悬置的初始静刚度，一般为经验值。假设式(14)中所有频率约束条件的左、右区间概率度均要求为1.0。

表1 动力总成在GCS中的转动惯量和惯性积(kg·m2)Tab.1 Inertia properties of the powertrain in the GCS(kg·m2)

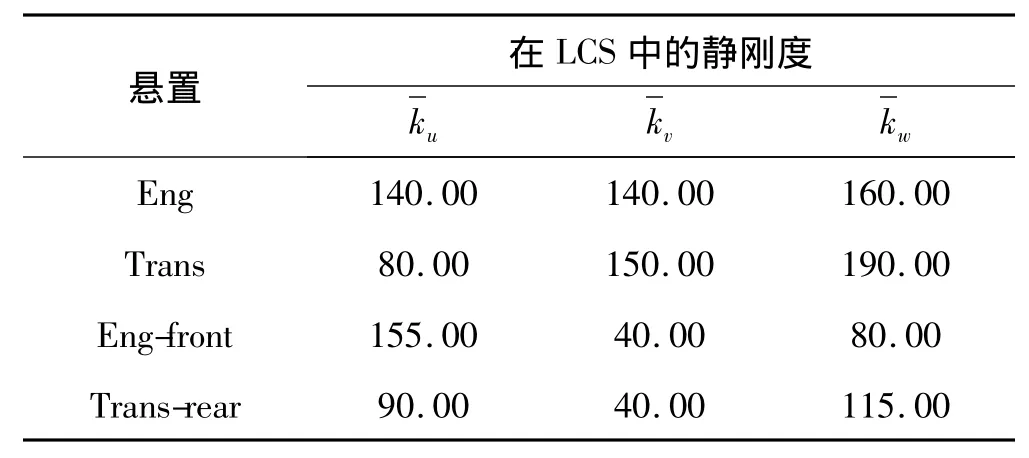
表2 悬置的静刚度(N/mm)Tab.2 Static stiffness of each mount(N/mm)

表3和表4分别给出了优化前的悬置系统频率和解耦率的区间分析结果。由表3可知，用文中提出的改进区间截断方法计算得到的频率的近似区间值精度很高，经计算，最大的相对误差仅为0.043%;而由文献［11］中方法计算的区间值普遍宽于本文方法得到的区间值，最大相对偏差为2.54%。

由表4可知，由本文方法计算的解耦率近似区间值的计算精度较好，经计算，最大的三个相对误差分别为11.33%、10.82% 和 7.83%，其它的相对误差均在6%以下;而由文献［11］中方法计算的区间值的最大的三个相对误差分别为50.68%、47.04%和27.68%。这表明，文中提出的区间分析方法精度较文献［11］中的方法有较大程度地提高。可以看出，优化前悬置系统的解耦率较低，并且区间半径较大，表明该悬置系统性能的稳健性较差，需进行悬置刚度的优化匹配。

优化结束后，表5、表6分别给出了当确定性优化最优刚度和区间优化最优刚度值波动时，解耦率和频率的变化区间。从表5可知，区间优化和确定性优化均可较大程度地提高悬置系统的解耦率;区间优化最优刚度值处的解耦率稍低于确定性优化，这是因为在区间优化模型中考虑了解耦率的稳健性要求，所以不可避免地导致解耦率稍有降低，两者是不可兼得的。但是，从表6可知，在区间优化最优刚度值处的各阶频率变化区间的上界大多小于确定性优化，从而可以提高各频率约束条件的区间概率度，即稳健性。

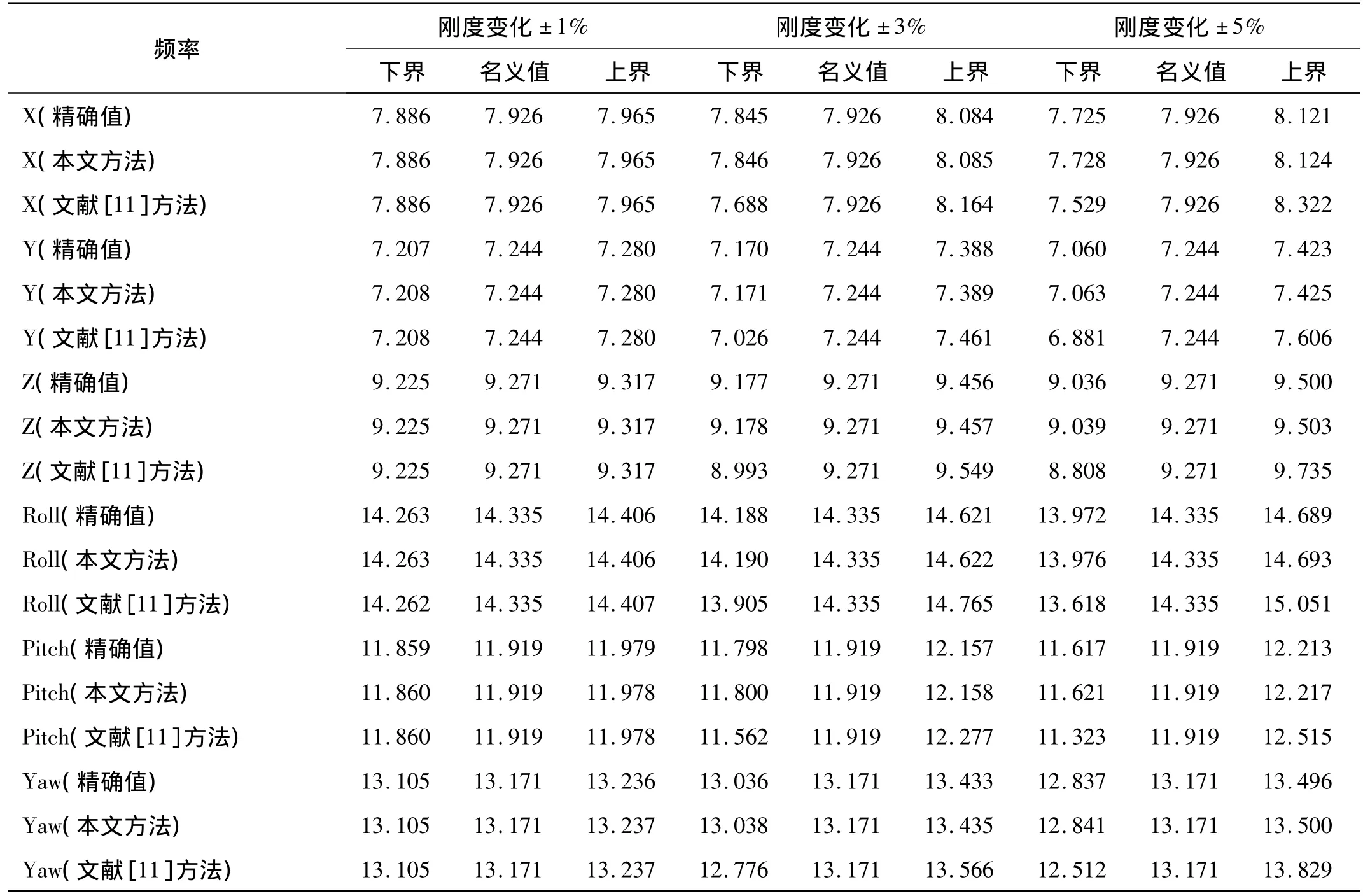
表3 优化前悬置系统固有频率的区间分析结果(Hz)Tab.3 Variation intervals of the initial frequencies of the powertrain mounting system(Hz)

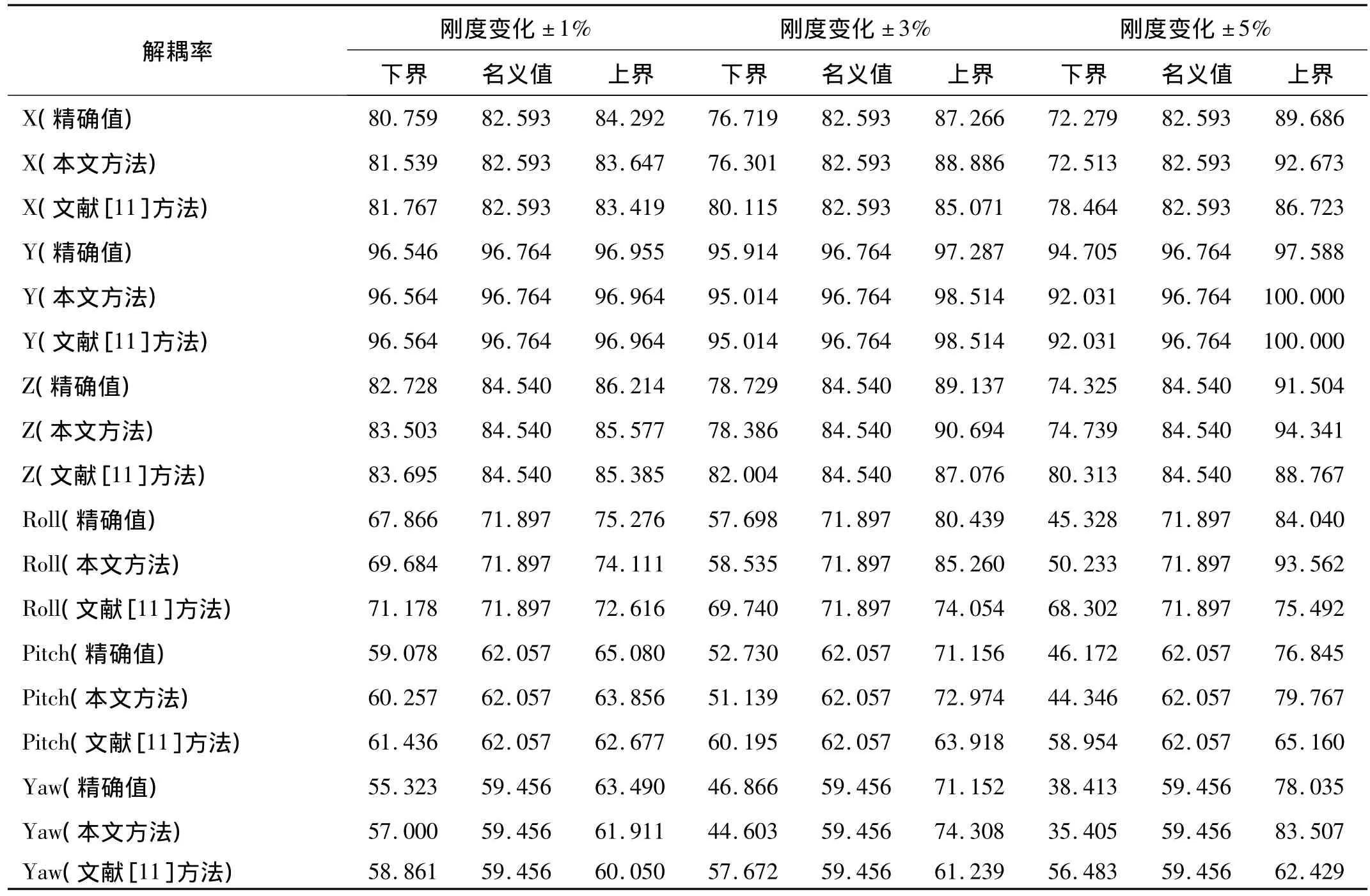
表4 优化前悬置系统解耦率的区间分析结果(%)Tab.4 Variation intervals of the initial decoupling ratios of the powertrain mounting system(%)

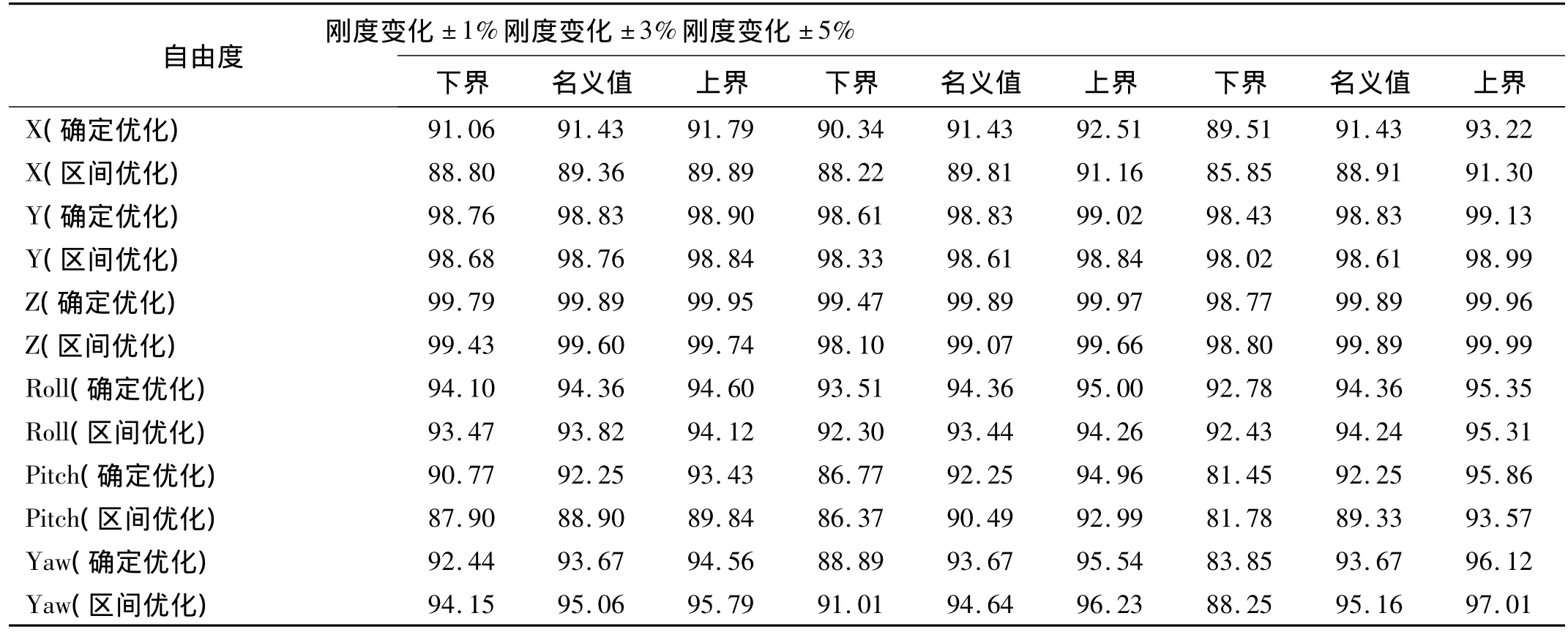
表5 优化后悬置系统解耦率的变化区间(%)Tab.5 Variation intervals of the decoupling ratios after optimization(%)

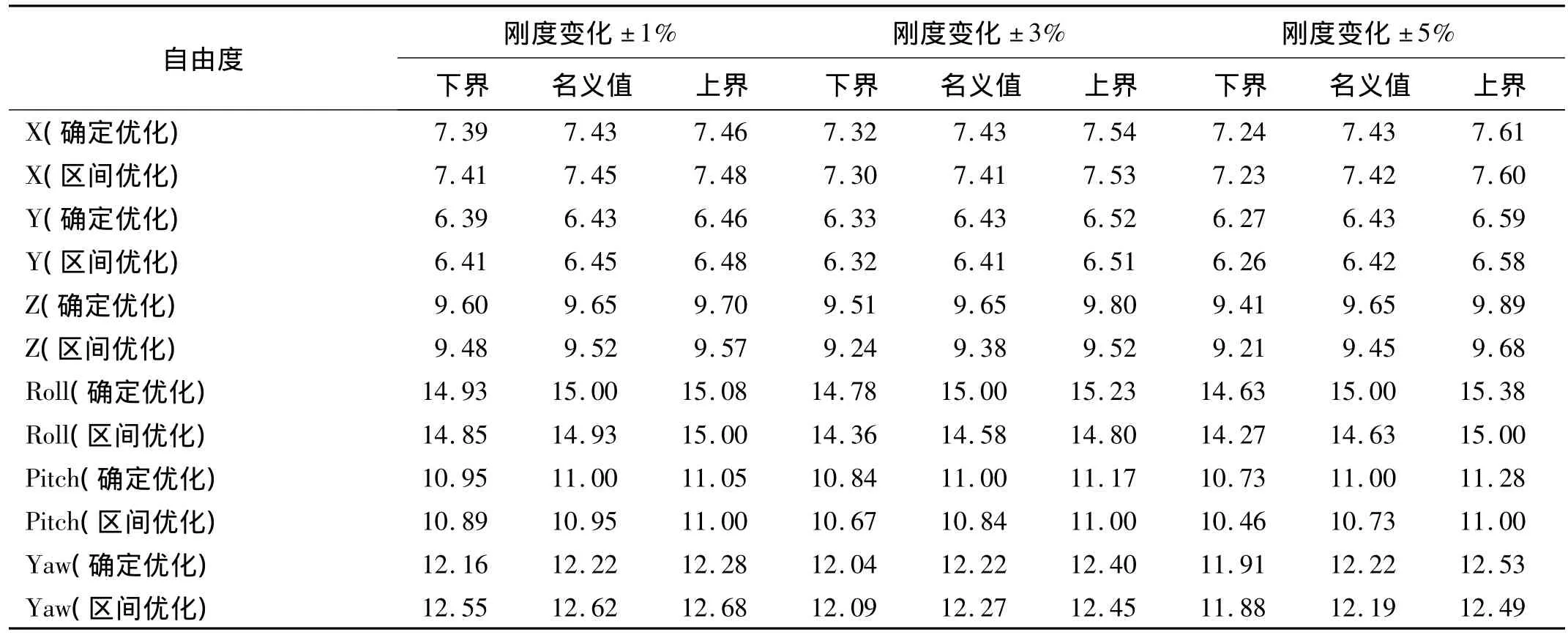
表6 优化后悬置系统固有频率的变化区间(Hz)Tab.6 Variation intervals of the frequencies after optimization(Hz)

表7给出了在确定性优化和区间优化最优刚度值处，式(14)中各约束条件的左、右区间概率度。可以看出，当最优刚度值有所波动时，在区间优化最优刚度值处的各约束条件左、右区间概率度均要大于或等于确定性优化，稳健性有较大幅度的提高，在Roll和Pitch方向尤为明显。

一般的，对沿Z轴(垂直方向)和Pitch方向(绕发动机曲轴扭转方向)的解耦程度要求较高，其它方向解耦程度可适当放宽要求。假设要求Z轴和Pitch方向的解耦率高于90%，表8给出了优化前后沿Z轴方向和Pitch方向的解耦率的区间可靠度。由表8可知，优化前Z轴和Pitch方向解耦率的区间可靠度几乎均为零。这表明该悬置系统刚度参数的匹配不合理，不能满足沿Z轴方向和Pitch方向的解耦率要求。

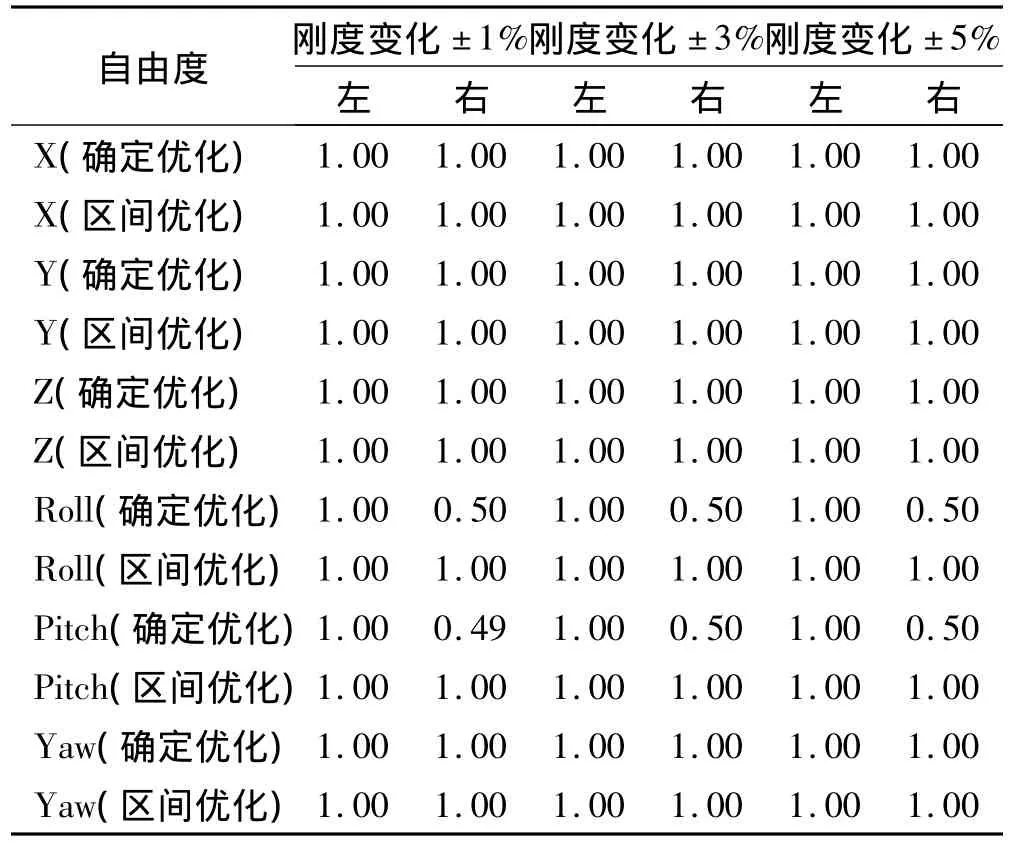
表7 优化后悬置系统频率约束的区间概率度Tab.7 Interval probability degrees of the constraints as the optimal design variables vary around their nominal values

由表8可知，区间优化和确定性优化都能使Z方向的区间可靠度达到1.0，解耦率都达到98%以上，并且相差很小，可以忽略不计。在Pitch方向，虽然区间优化结果的区间可靠度稍低于确定性优化，但从实际解耦率的变化区间来看，区间优化较优化前大幅度提高了该方向的解耦率，并且区间优化对应的解耦率区间半径要小于确定性优化，从工程角度来看，区间优化方法取得了较好地优化效果。

表8 优化前后悬置系统沿Z轴和Pitch方向解耦率的区间可靠度Tab.8 Interval reliabilities of the decoupling ratios in Z and Pitch directions as the stiffness parameters vary around their nominal values

另外，从表6也可以看出，在Roll和Pitch方向，确定性优化结果对应的频率变化区间的上界均超过了约束范围，这意味着动力总成与其它部件可能产生共振。因此，区间优化方法在保证不产生共振的情况下，稍微降低Pitch方向的解耦率是可以接受的。

6 结论

为使悬置系统的性能更加稳健，提出了悬置系统解耦率和频率的区间优化方法，对某轿车悬置系统的悬置刚度进行了稳健性优化。具体结论有:

(1)提出的区间优化方法能有效增大悬置系统各方向的解耦率，并提高解耦率的稳健性。与确定性优化方法相比较，区间优化方法可以较大幅度地提高频率的稳健性;

(2)可根据具体问题中优化目标和约束条件的相对重要程度给定约束条件的区间概率度，较确定性优化方法更加灵活实用;

(3)区间优化方法在设计阶段综合考虑各种不确定因素对优化结果可能造成的影响，能得到抗噪能力较强的稳健优化方案。

(4)动力总成质量和惯量参数也存在测量误差，为更全面地对悬置系统进行不确定性分析和优化，应该将它们也看作区间变量，这部分工作将另文介绍。

［1］吕振华，范让林.动力总成悬置系统振动解耦设计方法［J］.机械工程学报，2005，41(4):49-54.

［2］上官文斌，吴 杰.含液阻悬置振动系统的时域响应计算与优化方法［J］.机械工程学报，2008，44(9):106-112.

［3］徐石安.汽车发动机弹性支承隔振的解耦方法［J］.汽车工程，1995，17(4):198-204.

［4］Qatu M，Sirafi M，Johns F.Robustness of powertrain mount system for noise，vibration and harshness at idle［J］.Proc.Instn Mech. Engrs， PartD， JournalofAutomobile Engineering，2002，216(D10):805-810.

［5］ Sirafi M，Chang Y P.Robustness of mount systems for idle NVH，Part 1:Center of Gravity(CG)mounts［J］.International Journal of Vehicle Noise and Vibration，2006，2(4):317-333.

［6］翁建生，张 斌，汪 洋.汽车动力总成的区间模糊多目标优化［J］.现代车用动力，2006，3:28-31.

［7］吴 杰，上官文斌.基于6sigma的动力总成悬置系统鲁棒优化设计［J］.振动与冲击，2008，27(8):65-68.

［8］ Ben-Haim Y，Elishakoff I.Convex models of uncertainties in applied mechanics［M］.Amsterdam:Elsevier Science Publisher，1990.

［9］Hansen E.Global optimization using interval analysis［M］.New York:Marcel Dekker，1992.

［10］ Qiu Z P，Wang X J.Comparison of dynamic response of structures with uncertain non-probabilistic interval analysis method and probabilistic approach［J］.International Journal of Solids and Structures，2003，40(20):5423-5439.

［11］吕震宙，冯蕴雯，岳珠峰.改进的区间截断法及基于区间分析的非概率可靠性分析方法［J］.计算力学学报，2002，19(3):260-264.

［12］ Jiang C，Han X，Liu G R，et al.A nonlinear interval number programming method for uncertain optimization problems［J］.European Journal of Operational Research，2008，188(1):1-13.