圆柱壳体阻尼材料布局拓扑优化研究
2012-02-15李以农
李 超,李以农,施 磊,郑 玲
(重庆大学 机械传动国家重点实验室,重庆 400044)
为了抑制板、壳等结构的振动,可采用在结构表面敷设自由阻尼或约束阻尼的方法[1-3]。通常阻尼材料被完全覆盖于待控结构表面,结构设计的目的就是在尽量增大结构振动能量耗散前提下,确定阻尼材料的类型、层数及各层厚度。由于阻尼材料布局的空间拓扑是固定的,因此,要实现阻尼结构动力学特性的最优化是很困难的。
Bendsoe 和 Kikuchi[4]基于均匀化理论,提出了均匀化拓扑优化方法,成为连续体拓扑优化的重要方法。为解决求解过程中数值不稳定问题,Sigmund等[5]提出了实体罚函数法(SIMP)。连续体拓扑优化方法还有变厚度法和变密度法。尽管这些方法数学上严谨,但实际应用中却较为困难。后来,Xie等[6]提出了“渐进优化算法”,它通过逐步删除结构中利用率低的材料而得到一个满应力设计。渐进优化算法的关键是确定一个合适的准则来评价一个单元是“高效率单元”或是“低效率单元”,从而决定单元的删除或保留。渐进优化算法概念尽管在数学上并不很严格,但算法比较简单,计算效率较高,有较强的工程实用性。
杨德庆[7]针对阻尼结构的耗能特点,提出了阻尼胞单元和阻尼拓扑敏度等概念,对自由阻尼板进行了阻尼材料布局优化。韦勇[8]研究了自由阻尼及约束阻尼板的拓扑优化问题,通过计算能耗最大的阻尼材料粘贴位置,提出了阻尼结构快速拓扑优化方法。此外,郭中泽等[9-10]对阻尼材料的布局优化进行了研究,荣见华、杜海珍等[11-14]提出一种基于应变能的结构拓扑双方向渐进优化算法,刘寅东[15]提出了通过力传递的路径来构造拓扑的拓扑优化思路求解连续结构的拓扑优化问题。李以农等[16]利用渐进优化算法,以模态阻尼比为目标函数对约束阻尼梁进行拓扑优化,取得了良好的效果。以上文献针对的优化模型都较为简单,梁和平板较多,而本文对圆柱壳体这一常用结构,做了自由阻尼和约束阻尼结构的拓扑优化分析,得到了两种不同结构下的最优拓扑布局,并分析了其模态对拓扑优化的影响。
圆柱薄壳结构在工程上有广泛的应用,如鱼雷外壳、飞机机身、舰船船体等,研究圆柱薄壳结构的阻尼减振及材料布局拓扑优化具有重要的理论意义和工程应用价值。本文采用渐进优化算法,研究圆柱壳体阻尼材料布局的拓扑优化问题。建立圆柱壳体阻尼减振拓扑优化模型,导出结构模态损耗因子对阻尼胞单元的灵敏度表达式,根据拓扑优化准则,通过逐步删除阻尼材料中灵敏度最低的单元,达到对圆柱壳体阻尼材料布局优化的目的。
1 圆柱壳体阻尼结构拓扑优化模型
阻尼结构振动能量消耗主要来源于阻尼材料剪切变形。因此,为实现结构最大的振动能量耗散,通常以结构模态损耗因子或结构某关键点的位移为目标函数,以阻尼材料删除率作约束条件,建立阻尼结构的拓扑优化模型。本文以圆柱壳体的模态损耗因子为目标函数,阻尼材料删除率作约束条件,阻尼胞单元有或无为设计变量,建立拓扑优化模型。设计变量为:

其中,n是阻尼胞单元总数。βi=1表明:壳体结构表面第i个单元位置有阻尼材料,βi=0表明:壳体结构表面第i个单元位置无阻尼材料。拓扑优化模型描述为:

2 灵敏度分析
由模态应变能方法可知,结构的第k阶模态损耗因子的计算公式为:

式中:Edk为结构中阻尼材料的第k阶模态应变能;Esk为结构的第k阶模态应变能;ηd为阻尼材料损耗因子。
当第i个单元阻尼材料被删除时,结构的第k阶模态损耗因子的变化量为:

在渐进优化(ESO)方法中,由于删除单元数量在每次迭代中是有限的,因此,做如下近似:

其中:Edki为第k阶模态中第i个阻尼材料单元的应变能。
由(4)式~(6)式可得:

式(7)表示第i个阻尼材料单元删除后,引起结构第k阶模态损耗因子的变化量,即为目标函数对设计变量的灵敏度:

前M阶模态损耗因子对设计变量的灵敏度则为:

这里,ωk为权重系数,可以根据模型对某阶模态的敏感程度,有一定的变化,且满足:

对阻尼材料进行布局优化,就是逐步删除灵敏度绝对值最小的阻尼胞单元,使结构模态损耗因子沿着最缓慢的路径下降,使结构在一定阻尼材料用量下,保持损耗因子最大化。
3 优化计算流程
采用ANSYS参数化设计语言(APDL),编制优化设计程序。
首先,建立有限元分析模型,计算各阶模态的应变能,然后按照式(9)进行灵敏度分析,设定要删除的阻尼单元数量,去除灵敏度最小的那部分单元。删除最小灵敏度单元后,留下的单元即为求得的每一轮的拓扑优化结果,每一轮优化结束后,都要检查约束条件是否满足,如果不满足,迭代继续;如果满足,停止迭代输出结果。
此时,阻尼材料空间拓扑分布即为拓扑优化结果。因此,设计步骤可描述为:
(1)建立有限元分析模型;
(2)模态分析,计算结构阻尼单元和非阻尼单元每阶模态对应的模态应变能;
(3)由式(8)或式(9)计算目标函数对各阻尼单元设计变量的灵敏度;

图1 拓扑优化程序流程图Fig.1 Topological optimization program flow chart
(4)设定每次删除的阻尼单元数量;
(5)删除灵敏度最小的阻尼胞单元;
(6)判断是否达到约束条件,如果不满足,迭代继续,如果满足,迭代停止,输出计算结果。
拓扑优化流程图见图1所示。
4 数值算例
4.1 自由阻尼材料最优布局
一圆柱形薄壳,两端面受到径向和轴向约束。长为100 mm,内径为250 mm,外径260 mm,基层的杨氏模量为109 GPa,密度为4 440 kg/m3,泊松比为0.34;在圆柱形薄壳外表面覆盖一层粘弹性材料,厚度为1 mm,杨氏模量57 MPa,密度为1 140 kg/m3,泊松比为0.3,损耗因子为1。采用solid45单元对圆柱基壳和粘弹性阻尼材料划分网格。
在控制阻尼材料用量条件下,搜寻粘弹性阻尼材料的最优拓扑分布,使复合圆柱壳体的6、8、10阶模态损耗因子平均值最大,即各阶加权系数为1/3。
图2~图5分别是粘弹性阻尼材料删除率为20%、40%、60%和80%条件下的阻尼材料最优拓扑分布,灵敏度分别为 1.624 5 ×10-7、2.23 ×10-7、2.79 ×10-7和4.3×10-7。图6是损耗因子平均值随阻尼材料删除率的变化。图7为材料删除率随迭代次数增加的变化曲线。从图2~图5可知,由于两端面存在约束,模态损耗因子对阻尼胞单元的灵敏度较小,先被删除。此外,周向波节线处的灵敏度也较小,随着删除率增加,也将被删除。从图6可以看出:损耗因子平均值随阻尼材料删除率增加而减少,但下降速度并不是很快,表明:采用拓扑优化技术,可充分利用阻尼材料的空间拓扑布局,使结构保持较高的振动能量耗散特性。图7可以看出每次迭代删除的阻尼单元数大致不变,说明了迭代过程比较稳定。


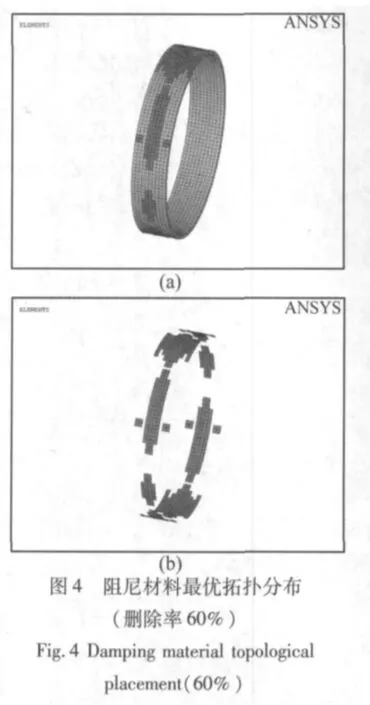
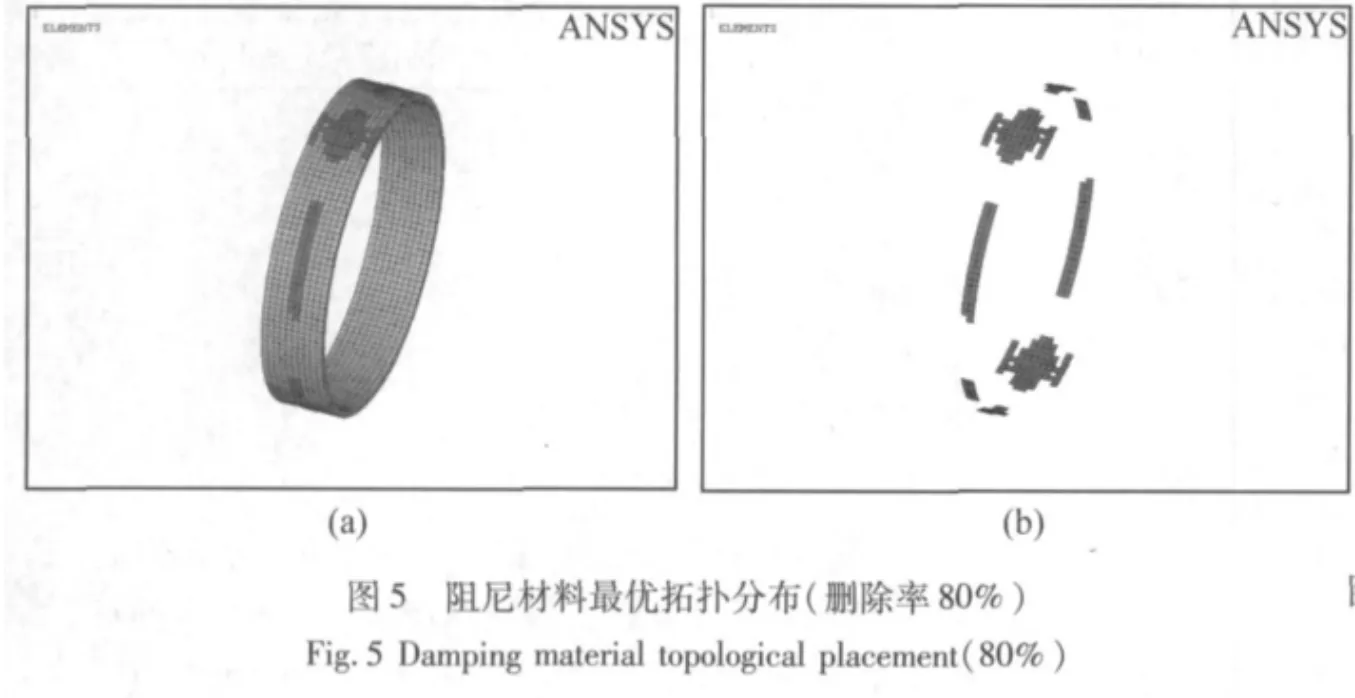


图7 阻尼材料删除率随迭代次数变化Fig.7 Change of damping material delete rate with iteration number
4.2 约束阻尼材料最优布局
一圆柱形薄壳,两端面受到径向和轴向约束。长100 mm,内径250 mm,外径260 mm,基壳杨氏模量为109 GPa,密度为4 440 kg/m3,泊松比为0.34;在基壳上覆盖一层粘弹性阻尼材料,厚度为1 mm,杨氏模量为57 MPa,密度为 1 140 kg/m3,泊松比为 0.3,损耗因子为1;在粘弹性阻尼材料上再覆盖一层约束层,厚度为1 mm,杨氏模量为210 GPa,密度为7 800 kg/m3,泊松比为0.3。基壳与粘弹性夹心层,采用solid45单元划分网格,约束层采用shell63单元划分网格。
在控制约束阻尼材料用量条件下,搜寻约束阻尼材料的最优拓扑分布,使约束阻尼圆壳的6、8、10阶模态损耗因子的平均值最大,即各阶加权系数为1/3。
图8~图11为约束阻尼材料删除率为20%、40%、60%和80%条件下的拓扑优化布局,灵敏度分别为5.43 ×10-4、8.41 × 10-4、1.25 × 10-4和 1.36 × 10-3。从图8~图11可知,灵敏度较低的阻尼胞单元处于两端面以及周波节线处,当删除率为60%时,这种效应变得更加明显。图12为损耗因子平均值随约束阻尼材料删除率的变化。图12表明:删除率小于20%时,模态损耗因子比全覆盖结构还略有升高,删除率达40%时,模态损耗因子与全覆盖结构相当,继续增大删除率,则模态损耗因子开始下降,说明删除的前40%阻尼材料对模态损耗因子的影响不大,但整个附加质量却减轻了。由此带来的结果是阻尼材料用量减少,附加质量减轻,而耗能作用不变,这就是采用拓扑优化布局的效应。图13为材料删除率随迭代次数增加的变化曲线。从图13可以看出:每次迭代删除的阻尼单元数大致不变,说明了迭代过程比较稳定。
通过对优化模型的模态分析可知,圆柱壳体模态振动关于壳体中心轴对称,是典型的空间对称,而从自由阻尼结构和约束阻尼结构拓扑优化布局来看,阻尼材料分布也是关于圆柱壳体中心轴对称的,说明模态振型和模态损耗因子灵敏度有着密切的联系。

图8 约束阻尼材料最优拓扑分布(删除率20%)Fig.8 Constraint damping topological placement(20%)

图9 约束阻尼材料最优拓扑分布(删除率40%)Fig.9 Constraint damping topological placement(40%)

图10 约束阻尼材料最优拓扑分布(删除率60%)Fig.10 Constraint damping topological placement(60%)

图11 约束阻尼材料最优拓扑分布(删除率80%)Fig.11 Constraint damping topological placement(80%)

图12 约束阻尼模态损耗因子随删除率变化Fig.12 Change of constraint damping loss factor of modality with delete rate
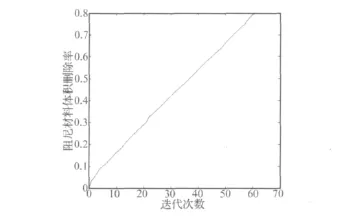
图13 约束阻尼材料删除率随迭代次数变化Fig.13 Change of constraint damping material delete rate with iteration number
5 结论
采用渐进优化算法(ESO),以阻尼结构模态损耗因子最大化为目标,阻尼材料删除率为约束条件,阻尼胞单元为设计变量,对自由阻尼以及约束阻尼材料布局进行了拓扑优化。研究了阻尼结构模态损耗因子对阻尼胞单元位置的灵敏度,导出灵敏度计算表达式。研究结果表明:约束阻尼结构的阻尼效果优于自由阻尼结构,且圆柱壳体模态振型和模态损耗因子灵敏度服从相同的空间分布规律,对自由阻尼或约束阻尼进行布局优化,能使圆柱壳体以较小的附加质量,获得较大的振动能量耗散,显著降低圆柱壳体的振动响应。采用ANSYS参数化设计语言(APDL),编写基于渐进优化方法(ESO)的拓扑优化程序,进行阻尼材料布局优化,在工程上是可行的,具有很好的工程实用性。
[1]林洪斌,赵德有,郑云龙.敷设粘弹性阻尼的加筋板振动和阻尼分析[J].中国造船,2002,43(3):40-47.
[2]Rao D K.Frequency and loss factor of sandwich beams under various boundary conditions[J].Journal of Mechanical Engineering Science,1978,20(5):271-282.
[3]李恩奇,雷勇军,唐国金,等.基于传递函数方法的约束层阻尼梁动力学分析[J].振动与冲击,2007,26(2):75-78.
[4] Bendsoe M P,Kikuchi N.Generating optimal topologies in structural design using a homogenization method[J].Comp.Mech.in Appl.Mech & Engrg.,1988,77:197-224.
[5]Sigmund O.Design of material structure using topology optimization[D].Denmark:Department of Solid Mechanics,Technical University of Denmark,1994.
[6] Xie Y M,Steven G P.Evolutionary structural optimization[M].Berlin,Heidelberg,New York:Springer,1997.
[7]杨德庆,柳拥军.自由阻尼层结构阻尼材料配置优化的拓扑敏度法[J].振动工程学报,2003,16(4):420-425.
[8]韦 勇,陈国平.一般阻尼结构的模态阻尼比优化设计[J].振动工程学报,2006,19(4):433-437.
[9]郭中泽,陈裕泽,侯 强,等.阻尼材料布局优化研究[J].兵工学报,2007,28(5):638-640.
[10]郭中泽,陈裕泽.基于准则法的阻尼结构拓扑优化[J].宇航学报,2009,30(6):2378-2391.
[11]Rong J H,Xie Y M,Yang X Y,et al.Topology optimization of structures under dynamic response constriants[J].Journal of Sound and Vibration,2000,234(2):177-189.
[12]荣见华,姜节胜,胡德文,等.基于应力及其灵敏度的结构拓扑渐进优化方法[J].力学学报,2003,35(5):584-590.
[13]荣见华,唐国金,杨振兴.一种三维结构拓扑优化设计方法[J].固体力学学报,2005,26(3):289-296.
[14]杜海珍,荣见华,傅建林,等.基于应变能的双方向结构渐进优化方法[J].机械强度,2005,27(1):72-77.
[15]刘寅东,卞 钢.基于ANSYS的结构拓扑优化及其二次开发[J].船舶力学,2006,10(2):120-125.
[16]李以农,谢熔炉,王 宜,等.约束阻尼结构拓扑优化设计的进化算法[J].重庆大学学报,2010,33(8):1-6.
