离心泵流体激励力的研究:蜗壳部分

蒋爱华，章 艺，靳思宇，章振华，黄修长，华宏星

(1.上海交通大学 机械系统振动国家重点实验室，上海 200240;2.中国船舶重工集团公司第704研究所，上海 200031)

离心泵的振动是广泛关注的问题，流体激励力是离心泵振动的主要原因之一。

从离心泵振动的研究历史来看，对流体激励力的研究还相对较少。现有对离心泵流体激励力的研究主要集中于叶轮蜗壳模型的简化以及叶轮在流体激励力作用下的涡动情况［1-2］、作用于叶轮上流体激励力的简化以及此时离心泵转轴的临界转速［3］、流体激励作用下离心泵蜗壳的结构辐射噪声与内部流体噪声［4-6］等。

其中，对叶轮蜗壳模型的简化还主要集中于二维模型［7］。这些模型对促进认识叶轮在流体中的运动过程有非常重要的作用，但也有其局限。一方面该模型未考虑带动叶轮转动的转轴，无法研究转轴与叶轮之间的相互作用力;另一方面二维模型也无法研究叶轮的陀螺力矩。

对作用于叶轮上流体激励力的简化以及此时离心泵转轴的临界转速的研究，还主要是基于传统转子动力学方法对流体激励力进行简化，即将流体对叶轮的激励力简化为叶轮的附加质量，该附加质量为叶轮内所包含流体20%-40%的质量，而后计算此转子模型的临界转速。这种方法可以不用计算真实的流体激励力，而只需从结构力学考虑系统的机械特性，因此工程中得到了广泛的应用［8］。

但这种简化方法有明显的缺陷:由于叶轮上增加了附加质量，所计算的转子系统临界转速与实际值将有较大偏差;另外同样流量下，随着叶轮转速的变化，实际叶轮所受的流体激励也将发生变化，而此简化模型中明显没有考虑转速不同附加质量的变化;且由于叶轮为轴对称结构而蜗壳流域为非对称流场，在叶轮转动过程中所受流体激励力也将为非轴对称形式。因此有必要对这种模型进一步改进。

对流体激励作用下离心泵噪声的研究主要集中于叶片与流体流固耦合诱发噪声简化模型的建立、汽蚀时离心泵内流场的噪声、蜗舌与流体流固耦合诱发噪声的实验研究［9-11］。采用CFD计算出离心泵蜗壳内表面的流体力，而后计算蜗壳向空气中声辐射的研究也得到了一定关注［6］。

但需要指出的是，由于工程中离心泵蜗壳常与带动叶轮转动的动力机械通过基座连接在一起，而流体激励叶轮，而后通过转轴传递至动力机械基座也将引起蜗壳的振动，因此将无法分辨引起蜗壳辐射噪声的主要激励源。并且离心泵与动力机械的共同基座常与其他板壳结构相连接，而离心泵向空气中辐射的噪声可能远小于这些板壳结构所辐射的噪声，此时离心泵向基座传递的振动加速则成为板壳结构向外辐射主要原因。

现阶段国内外还未查到研究离心泵内部流体对基座激励的相关文献。虽然运用CFD计算离心泵内部流场的研究已经比较广泛和深入［12-13］，但由于流体力学的研究者主要关注离心泵内流场的变化。同时，机械振动的研究者也主要关注激励作用下结构的响应与变形等［14］。流固耦合的研究者偏向于基于连续介质力学建立流体与固体区域的控制方程［15］，而后通过流固边界位移相等条件联系两组方程，并运用数值方法求解流场与固体结构各节点的位移，这种方法比单独先求解流场而后将流固边界上作用力用于固体结构的单向流固耦合方法具有更加准确的结果，但由于这种方法有一定难度，且选择流体控制方程时还主要应用势流中的伯努利方程，还无法满足离心泵这种流场中含有流动分离湍流流动的旋转机械的需要。

鉴于现有研究的不足以及通过试验研究流体激励力的困难，本研究将基于CFD技术，应用CFX对离心泵内流场进行非定常分析，而后通过积分最终得出运转过程中流体对离心泵结构的激励力。本研究共分为两部分，分别阐述流体对蜗壳与叶轮的激励作用，本文为前者。

1 离心泵内流场的计算

1.1 计算流体力学(CFD)基本理论

对于不可压常粘性流体湍流流动的离心泵内流场，其控制方程为雷诺方程。张量形式的雷诺方程如式(1)所示。

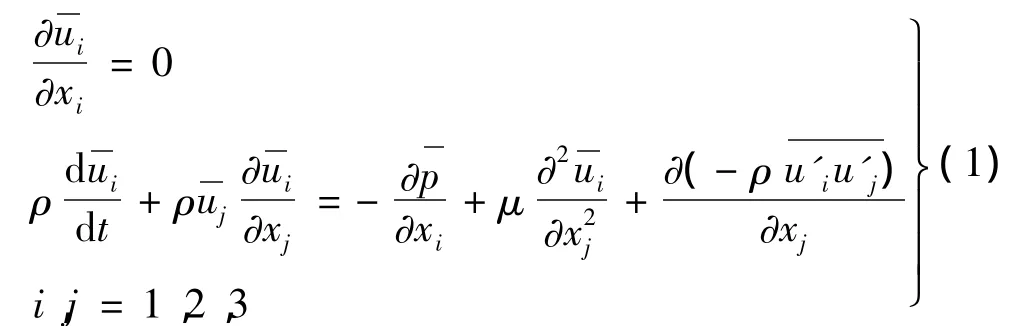
SSTk-w模式是一种双方程的湍流模式，在边界层以内采用湍动能方程k与湍动频率方程w，在边界层以外采用湍动能方程k与耗散率方程e，因此实际数值计算过程中总共需要求解的方程为六个。为了得到较准确的计算结果，采用SSTk-w模式时边界层以内需要有多层网格。

离散求解以上方程时，常采用有限体积法(FVM)［17-18］。本研究中采用的工具为CFX，是基于有限单元的有限体积法，更加容易得到收敛解。

1.2 流域几何模型的建立与网格划分

所研究对象为一单级单吸式离心泵，其额定工况下比转速为139。运用Por-E建立了离心泵内各流体域模型，共建立了七个流体域，包括离心泵进口流域、离心泵叶轮内流域、蜗壳内流域、平衡室流域、叶轮前盖板与蜗壳间隙流域(包括泄漏环处间隙)、叶轮后盖板与蜗壳间隙流域与蜗壳出口延长段流域。其中叶轮流域为旋转流域，而其余流域为静止流域。

延长蜗壳出口流域是为了使流场能够充分发展并达到稳定状态，以更加准确计算出离心泵内流场。另外，将平衡室流域也作为研究的对象是为了分析其对离心泵运转过程中轴向力的平衡作用。

各流域网格的划分均采用ICEM完成，所划分网格均为六面体，以加快计算过程的迭代收敛速度与稳定性。划分网格时，为了能够确保壁面底层网格在边界层以内，通过预估计算得出所划分网格的壁面当量厚度Yplus值，并调整底层网格使得Yplus值处于11.63与500之间，以确保底层网格处于对数率层以内［19-20］，并对底层网格进行了加密。

各流域网格划分完成后，导入CFX中通过Interface界面连接为一个整体，如图1所示即为所划分的离心泵内流域网格，其中坐标原点位于蜗壳对称平面与叶轮轴心交点处，空间方向如图中箭头所示，表1为各流域网格、节点数量与体积。当增加网格密度使得网格数量为表中网格数量的约1.5倍时，所得预估稳态流场与表中网格数量下所获得预估稳态流场的蜗壳对称平面压力分布与速度矢量图基本相同，则认为此时所得流场已为网格无关解。

1.3 稳态流场计算

为了能够准确计算出叶轮转动过程中离心泵内流场的变化情况，需要给定准确的初值，因此首先计算稳态流场以作为瞬态流场的初值，而稳态流场计算过程中各参数初始值均为零。

图1 离心泵流域网格Fig.1 Mesh of fluid volume in centrifugal pump

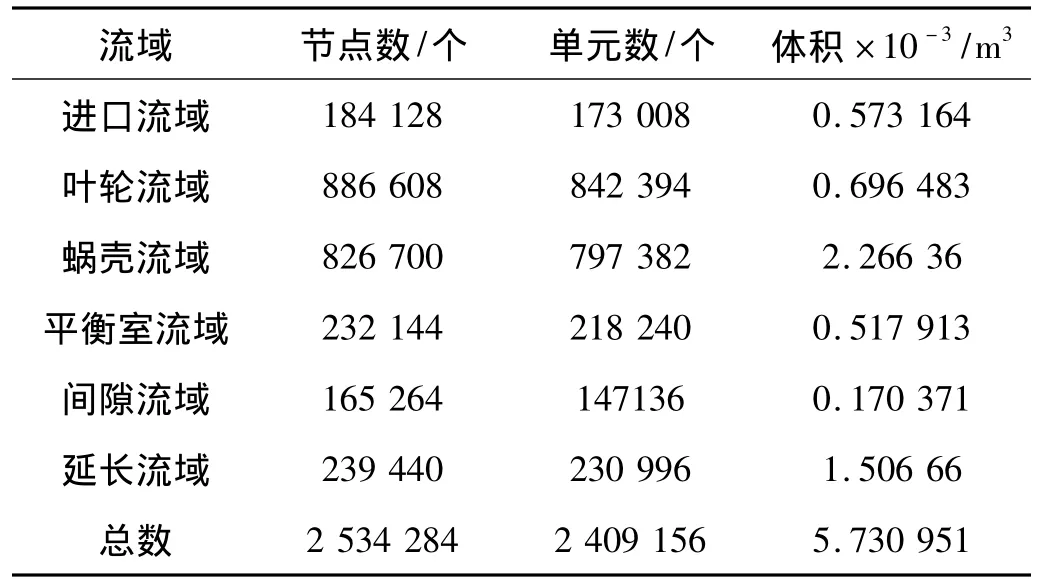
表1 各流域节点数、单元数与体积Tab.1 Nodes number，elements number and volume of different fluid parts

计算离心泵工况如图2所示，叶轮转速为额定转速2 930 n/min，流量为额定流量100 t/h，其吸入口轴线与主轴垂直于水平面，吸入口与水面垂直距离为395 mm，水面有一个标准大气压。因此在CFX中设置参考压力为1 atm，进口边界条件分别为静压3 871 Pa(亦即395 mm水柱)，出口边界条件设置为流量，其余边界设为固壁无滑移条件，湍流模式选择SST模式，计算过程中对式(2)积分所得公式进行二阶中心差分，收敛标准采用各参数平均残差值小于1E-5。

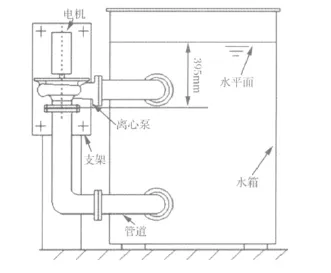
图2 离心泵工况示意图Fig.2 Sketch map of centrifugal pump working condition

1.4 瞬态流场计算

如表2中所示分五个阶段计算了离心泵瞬态流场，第一个阶段流场初始值为稳态流场计算结果，其余阶段初始值均以上一阶段最后一个时间步所得结果。采用了时间步长与收敛标准不同的五个阶段来计算流场是为了尽量消除数值计算过程的不稳定性与从稳态流场计算中叶轮位置不变到叶轮转动过程中流场的不稳定性，并提高结果的准确性。

从表2中可以看出，第一阶段的5个时间步中，叶轮每转动0.4°为一个时间步，整个过程中叶轮流域相对静止流域转动了2°;第二阶段的30个时间步中，叶轮每转2°为一个时间步，叶轮流域相对静止流域转动了60°;第三阶段的55个时间步中，叶轮每转12°为一个时间步，叶轮流域转动了660°;第四阶段采用了与第二阶段相同的时间步长计算了60步，叶轮流域共转动了120°;最后阶段的计算中采用与第四阶段相同的时间步长，共计算了180步亦即叶轮流域转动360°。其中，前四个阶段迭代计算中以残差小于1E-5为收敛标准，而为了用更加准确的流场得出流体激励力，第五个阶段收敛标准设置为残差小于1E-6。因此，所有计算过程完成以后，叶轮流域共转动了1 202°，共计330个时间步，此时叶轮以2 930 n/min的转速转动了0.068 5 s，叶轮每转一度需要的时间约为 5.688 3e-5s。

如图3示即为第四阶段瞬态流场计算中，叶轮转动60°所得XY截面的绝对压力分布变化。所显示的四个时刻中，每相邻两个时刻叶轮转角相差20°，初始时刻XY平面中轴心叶尖连线与通过叶轮轴心的蜗舌圆弧切线夹角(以下简称蜗舌切线)约为14°，而蜗舌切线与X轴夹角为30°。从图中可以看出第1步与第30步所得到的绝对压力分布有较高的相似性。

表2 瞬态计算时间步设置Tab.2 Setup on time step of transient simulation

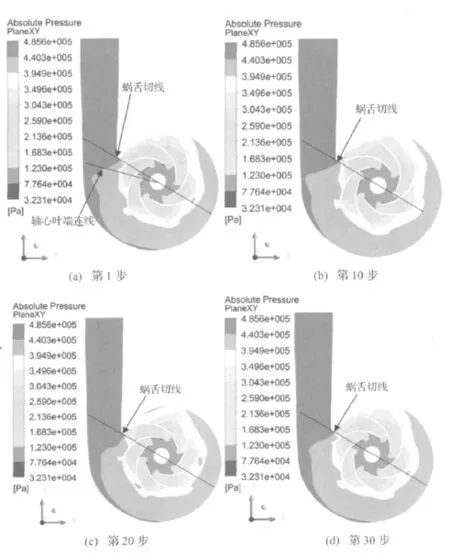
图3 叶轮转动60°过程中流场绝对压力变化Fig.3 Changes on absolute pressure within 60 degrees of rotating impeller

表3 各方向上合力的统计参数Tab.3 Statistical parameters of forces composition on different directions

2 流体对蜗壳的激励力

2.1 流体激励力变化过程

基于以上所得离心泵内流场，运用CFX后处理模块对蜗壳流域固体界面表面力进行积分，该表面力包括了流体对固体界面的总压以及由固体界面处流体剪切运动所带来的粘滞力，从而得出离心泵内部固体界面所受三个方向的流体合力。如图4示即为330步瞬态计算过程中蜗壳所受空间三个方向上流体合力的变化情况与所建立的蜗壳质量-弹簧振动模型。

从图4出，蜗壳各方向上流体合力在叶轮转动过程中均围绕一定值上下波动。特别是时间步大于90步以后的波形其波动周期更加明显，且每30个时间步为一个波动周期，对应叶轮转角为60°，亦即叶轮每个叶片经过蜗舌切线时各向合力会出现一次波动。另外，X向流体合力相对小于其他两个方向上的合力，波形围绕零值上下波动。Y向流体合力保持为负值，表明蜗壳所受Y向合力始终从蜗壳指向基座方向，亦即垂直于蜗壳出口与流体流出方向相反。Z向流体合力保持为正值，表明蜗壳所受Z向流体力始终从离心泵进口指向平衡室方向，亦即垂直于蜗壳进口方向与流体流入方向相同。

从图4中还可以看出，各向合力从第36至第90个时间步的波形相对于90步以后的波形有更小的波动周期。这是因为第36至第90个时间步以叶轮流域每旋转12°作为一个时间步，而第90个时间步以后均以叶轮流域每旋转2°作为一个时间步，当以时间步数为横轴时，同样时间步数前者叶轮转角相当于后者的六倍。

另外，图中前35个时间步波形周期不明显。这一方面是由于所对应的叶轮转角较小且时间步不一致，看不出波动周期，另一方面也是由于相邻的时间步采用不同时间步长进行迭代计算时，将会出现数值的不稳定，第35、第36个时间步与第90、第91个时间步处，Z向合力的两个尖峰更明确的说明了这一点。因此，在进行蜗壳的流体激励力响应时，运用远离时间步长发生变化处的流体激励力将更加准确。

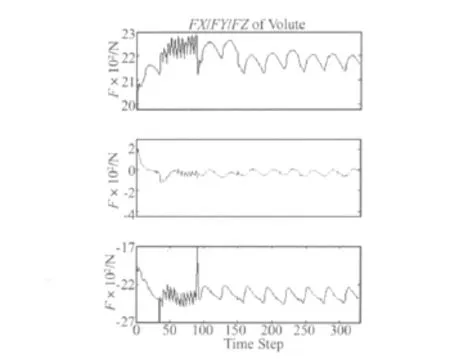
图4 蜗壳三个方向上流体激励合力Fig.4 Three direction inciting force on volute by fluid

以第五阶段180个时间步所得结果进行频谱分析，其功率谱如图5所示，统计参数如表3所示。从图5中可以看出，蜗壳各向流体合力均以293 Hz为基频，与叶片通过频率相同;与其它两向流体合力相比，Y向合力具有更大的波动幅值，其二阶频率的谱值就已经高于其余各向合力基频谱值。

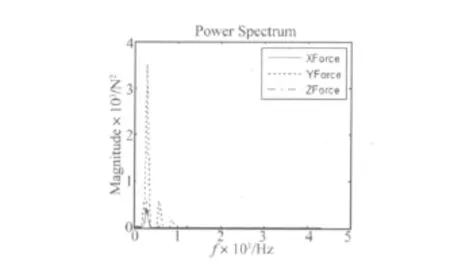
图5 X、Y与Z向合力功率谱Fig.5 Power spectrum of forces composition on X，Y and Z directions

2.2 流体激励力数学模型的建立

由2.1可知，叶轮以一定转速转动过程中，蜗壳所受各向流体合力均有明显的周期变化，若能够根据该规律建立不同转角下蜗壳受流体力的数学模型，对进一步研究离心泵中的流体激振将有重要意义。由于第五阶段所得结果更加准确，因此以该阶段的180个时间步所得结果进行数学模型的建立。

为了使所建立模型将流体激励力与叶轮的转角相对应，本研究分别采用最小二乘多项式与傅里叶级数对原始信号进行逼近，所有过程均运用Matlab中完成现有函数完成。

首先将三个方向流体合力按照其周期进行平均，每30个时间步为一个周期，对应叶轮转角为60°，得出用于逼近的原始信号，而后采用九次多项式对所得信号进行了最小二乘的拟合。

运用傅里叶级数对流体三个方向上的激振力逼近时，采用未加窗FFT变换后信号的激振力基频幅值作为正弦波的幅值，根据正弦波波峰与原始波形的波峰修正正弦波的相位。

三向流体激励力的原始信号、九次多项式拟合波形与傅里叶级数波形如图6(a)中所示。拟合信号与原始信号的标准偏差如表4所示。从图与表中可以看出，与基频正弦波相比较，九次多项式拟合与原始信号有更小的偏差，这是因为一方面基频正弦波只应用了基频幅值作为逼近波形的幅值，具有较大的能量损失，另一方面原始波形与标准正、余弦波也相差较大。但同时从图中也可以看出，九次项式拟合方法所得到的波形与原始信号仍然有较大的差距，并且多项式所需要拟合的阶次也比较高，对下一步运用质量弹簧模型计算离心泵蜗壳的振动带来不便。因此，还需要寻找其他建模的方法。

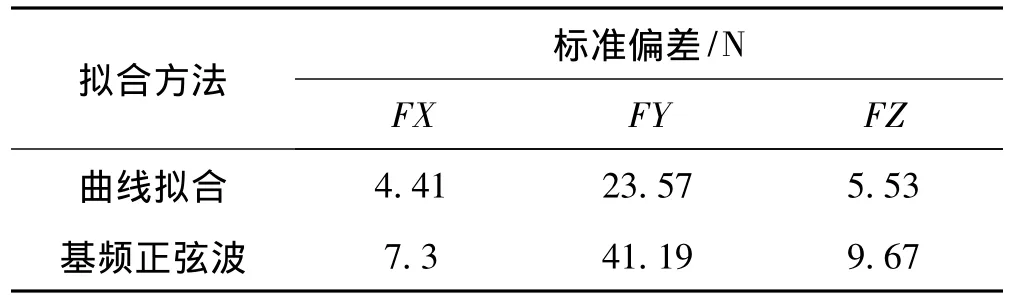
表4 不同拟合信号与原始信号的标准偏差Tab.4 Standard error between original signal and different fitting signals

从图6(a)中还可以看出，三个波形均呈现出先起始点单调降低至波谷，而后由波谷单调上升至波峰，最后由波峰单调下降至末点的趋势，因此如果采用分段曲线拟合则可以用较低的阶次得到较好的结果。

图6(b)所示即分别为对X向、Y向与Z向静止流域固体界面合力的分段拟合。拟合时以起始点到波谷为第一段，波谷至波峰为第二段，剩余的为第三段，各段拟合是根据具体情况选择所需要拟合的阶数，并且各横轴也由时间转化为对应的叶轮转角。从图中可以看出X向流体合力波谷与波峰所对应的转角为18°与42°处，由于初始时刻XY平面的轴心叶尖连线与蜗舌切线之间的夹角为14°，亦即X向流体合力最小与最大值分别出现于叶尖绕轴心转动通过蜗舌4°与28°处;类似地Y向流体合力幅值最大出现于叶尖处于轴心蜗舌连线时，最小幅值出现于轴心叶尖连线绕叶轮轴心转动通过蜗舌切线后14°处;Z向流体合力最小值对应的叶轮转角与Y向流体合力最大幅值处叶轮转角相同，但最大值对应的叶轮转角与X向最大值处叶轮转角相同。

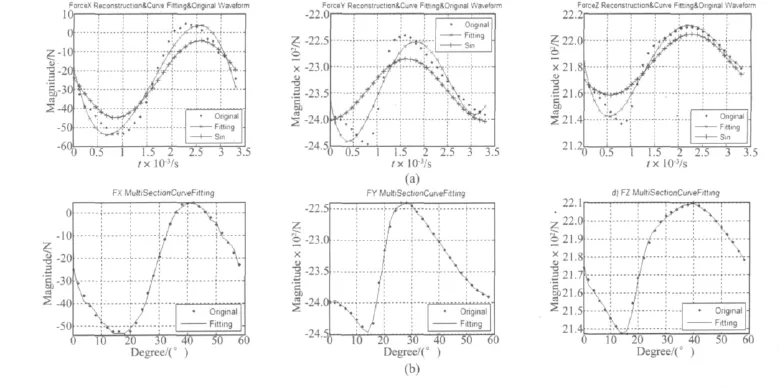
图6 蜗壳三向流体激力拟合Fig.6 Polynomial fitting of three-direction composite fluid forces on volute

从图6(b)中可以看出，各向合力在分三段拟合以后的结果明显好于图6(a)中所示拟合结果，拟合信号与原始信号的标准偏差分别为 1.09、3.51 与 1.31，也远小于表4中所示两种方法所获得的标准偏差，并且分三段拟合时各段多项式最高仅为三阶，三个方向上流体激励合力波形分三段拟合所获得多项式分别如式(3)、式(4)与式(5)所示。

3 结论

(1)运用CFD计算了离心泵叶轮转动过程中的瞬态流场，并基于瞬态流场积分得出了蜗壳所受流体激励合力，结果表明，离心泵运转过程中蜗壳受到空间三个方向叶片通过频率的周期性流体激励力。

(2)对比分析整个计算过程中蜗壳流体合力并进行功率谱分析表明，三个方向的流体合力中，垂直于蜗壳出口平面方向的合力与流体流出方向相反并具有最大的波动幅值，垂直于蜗壳进口平面方向的合力与流体流入方向相同，正交于前两个方向的合力方向随着波动周期而改变并具有最小的波动幅值。

(3)对比分析单个周期内各向流体合力变化可知，垂直于蜗壳出口表面方向的流体合力与垂直蜗壳进口表面方向的流体合力的波谷值，均出现于叶尖转过蜗壳对称平面内穿过叶轮轴心的蜗舌圆弧切线处。

(4)分别运用九次多项式拟合、波动基频正弦波与三段多项式拟合近似各向周期性流体激励力，结果表明采用三段多项式拟合所建的数学模型与原始波形有最小的偏差，并且具有较低阶次。

［1］Adkins D R.Analyses of hydrodynamic forces on centrifugal pump impellers.PHD dissertation［D］.California Institute of Technology，1986.

［2］Adkins D R，Brennen C E.Analyses of hydrodynamic radial forces on centrifugal pump impeller［J］.Transaction of ASME，1988(3):20-28.

［3］袁振伟，楮福磊，林言丽，等.考虑流体作用的转子动力学有限元模型［J］.动力工程，2005(8):457-461.

［4］Langthjem M A，Olhoff N.A numerical Study of Flowinduced noise in a two-dimensional centrifugal pump［J］.Part I:Hydrodynamics.Journal of Fluids and Structures，2004，(19):349-368.

［5］Langthjem M A，Olhoff N.A numerical study of flow-induced noise in atwo-dimensionalcentrifugalpump.PartII:Hydroacoustics［J］.Journal of Fluids and Structures，2004，(19):369-386.

［6］ Jiang Y Y，Yoshimura S，Imai R，et al.Quantitative evaluation of flow-induced structural vibration and noise in turbomachinery by full-scale weakly coupled simulation［J］.Journal of Fluids and Structures，2007(23):531-544.

［7］Brennen C E.Hydrodynamics of pumps［M］.Oxford University Press，1994.

［8］闻邦春，顾家柳，夏松波，等.高等转子动力学［J］.机械工业出版社，2000.

［9］Howe M S.On the estimation of sound produced by complex fluid-structure interactions，with application to avortex interacting with a shrouded rotor［J］.Mathematical and Physical Sciences，1991(443):573-598.

［10］ Schmitz S.Reducing Pump noise in cooling tower applications［J］.World Pumps，2004(9):24-29.

［11］ Dong R，Chu S，Katz J.Effect of modification to tongue and impeller geometry on unsteady flow，pressure fluctuations，and noise in a centrifugal pump［J］. Journal of Turbomachinery，1997(119):506-515.

［12］郭鹏程.水力机械内部复杂流动的数值研究与性能预测［D］.西安:西安理工大学，2006，9.

［13］徐朝晖.高速离心泵内全流道三维流动及其流体诱发压力脉动研究［D］.北京:清华大学，2004，4.

［14］李德葆，苏铭德，诸葛洪程，等.流体激发结构振动响应预测模型及激振力的识别［J］.振动与冲击，1991，10(1):6-13.

［15］邢景棠，周 盛，崔尔杰.流固耦合力学概述［J］.力学进展，1997(2):19-38.

［16］ Menter F R.Two-equation eddy-viscosity turbulence models forengineering applications［J］. American Institute of Aeronautics and Astronautics.1994(8):1598-1605.

［17］ Eymard R，Gallouet T，Herbin R.Finite volume method［M］.Handbook of Numerical Analysis，1997.

［18］ Ferziger J H，Peric M.Computational methods for fluid dynamics［M］.Springer.-Verlag.2001.

［19］ Fluent Inc.，User's Guide［M］.Fluent Inc，2003.

［20］ Versteeg H K， Malalasekera W. An introduction to computational fluid dynamics:the finite volume method［M］.Wiley，New York，1995.